如何通过“r2”,沟通方与圆的面积关系

为了更好地探索方与圆面积之间的关系,可以按如下教学过程展开教学。
一、计算面积,感受“r 2”的作用
1.学生独立完成。
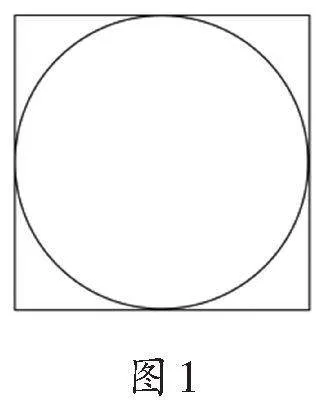
教师出示题目:已知图1中正方形的面积是16平方米,你能求出圆的面积吗?
2.全班进行教学反馈。
方法一:先求半径r,4×4=16(平方米),r=4÷2=2(米);再求圆的面积S=3.14×22=12.56(平方米)。
方法二:如果把正方形的边长看作2r,那么正方形的面积就是2r×2r=4r2,就可以求出r2=16÷4=4(平方米),所以,圆的面积S=4×3.14=12.56(平方米)。
方法三:因为圆的面积∶正方形的面积=[π]∶4,所以圆的面积S=16÷4×3.14=12.56(平方米)。
教师引导学生思考:圆的面积是[π]r2,正方形面积是4r²,约去r²后的面积比为[π]∶4。
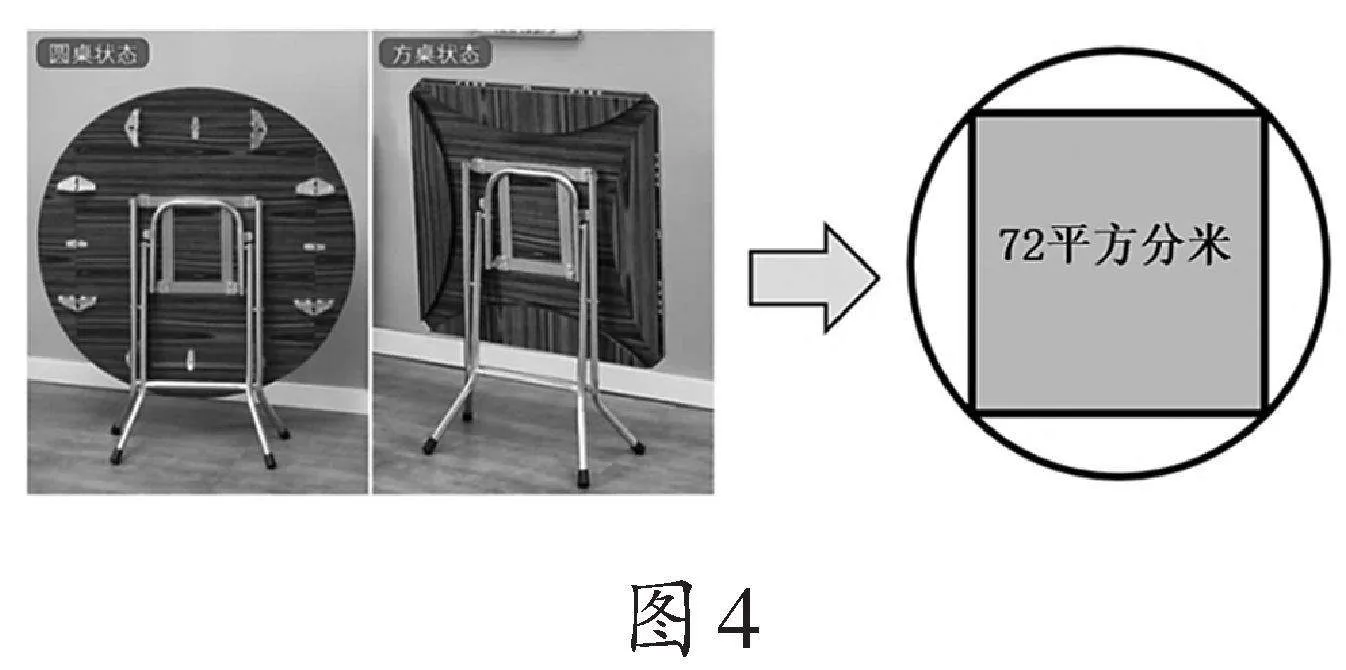
3.引导学生观OY1ch4Qb4R6AplaI7sDRVQ==察比较三种方法的相同点:三种方法在计算圆面积时都借助了r²。教师运用课件动态演示用阴影表示r²(如图2)。
4.巩固。
教师出示题目:如果图1中正方形的面积是20平方米,你能快速求出圆的面积吗?
全班交流后,引导学生思考:20÷4×3.14中的20÷4表示什么意思?
师生小结:20÷4就是一个小正方形的面积,也就是r²的大小。知道了r²,就可以求出圆的面积。
二、大胆想象,寻找“r 2”的图像
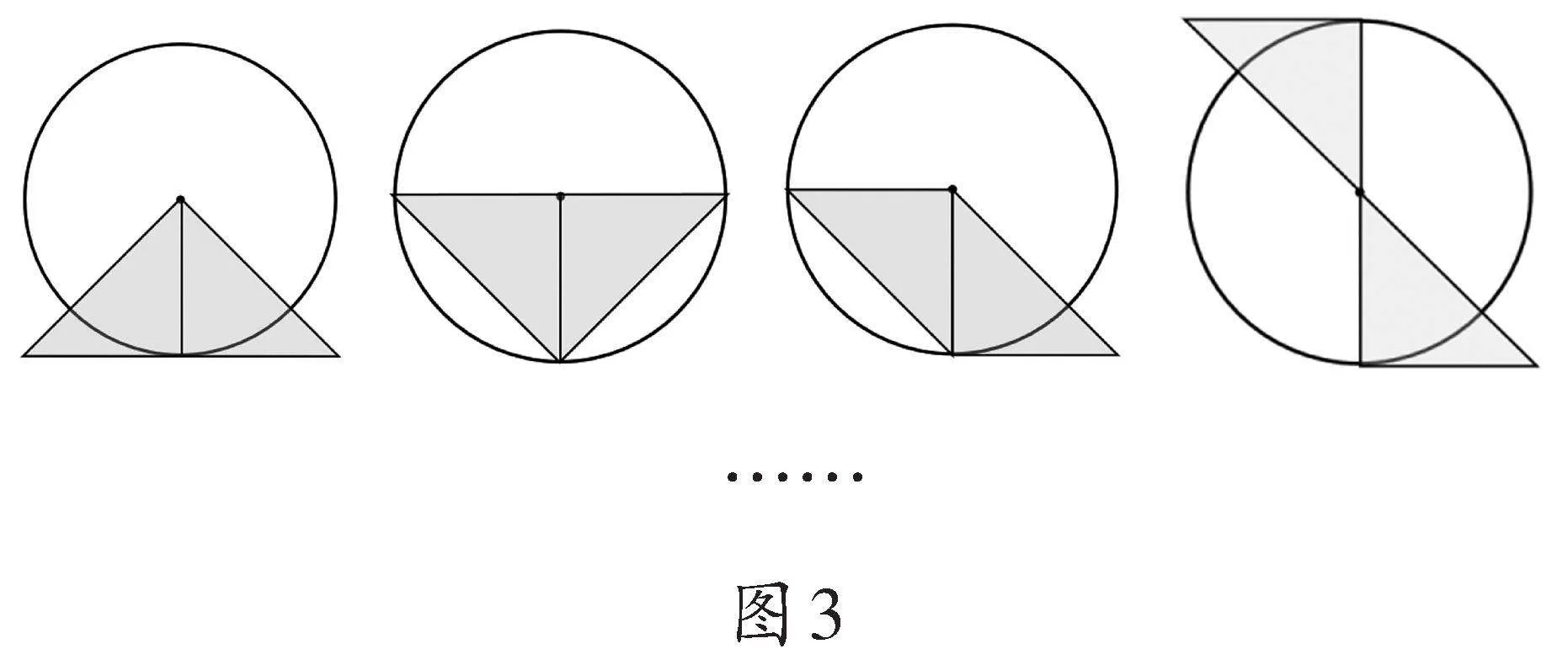
1.教师出示题目:如果圆的半径是r,请过圆心找到r²的大小,并用阴影表示出它的面积。(想一想,可以有多少种不同的图形?)
2.全班进行教学反馈,呈现不同学生的作品(如图3)。
三、解决问题,体验“r2”的应用
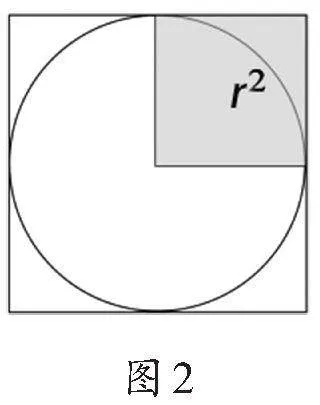
1.图4中的左图是生活中的圆形、正方形餐桌,如果它们的面积关系如右图,那么,正方形餐桌的面积是72平方分米时,请试求圆形餐桌的面积。(提示:可先找到r²)
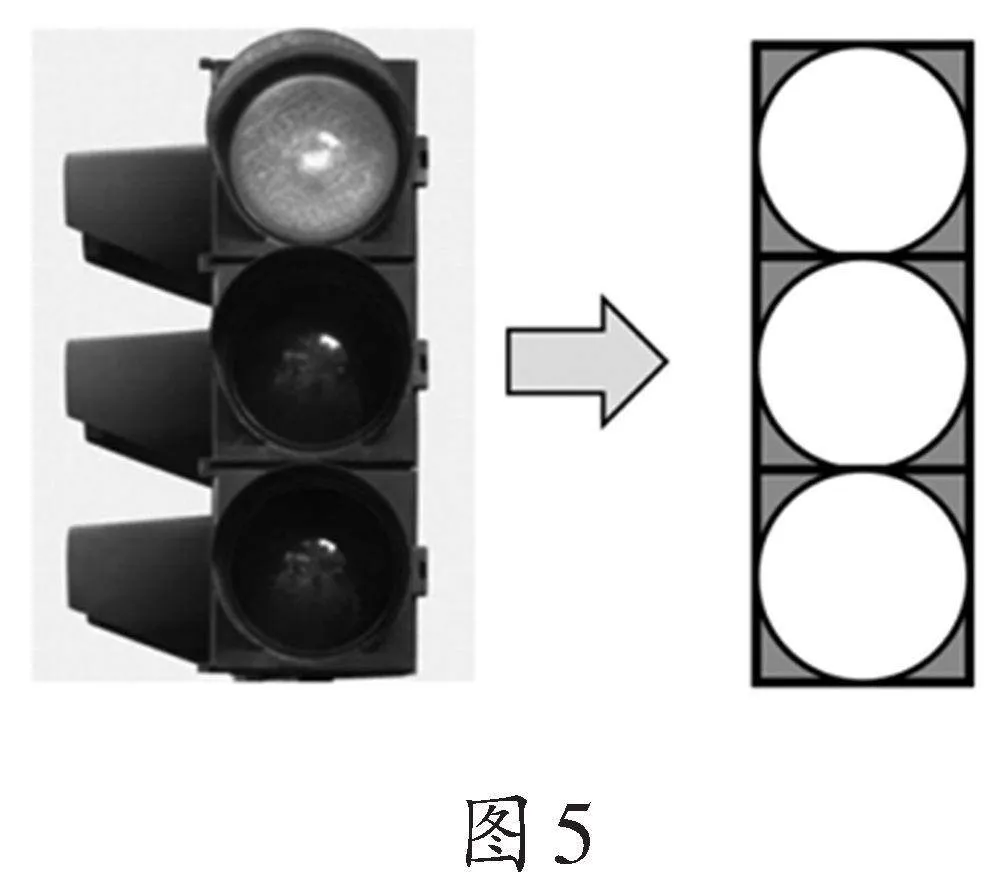
2.出示如图5的红绿灯图片,红绿灯是由3个大小相同的圆形组合而成,如果红绿灯正面所占的面积为75平方分米,那么请试求外框与红绿灯之间阴影部分的面积。
通过上述教学过程,学生在丰富的学习体验中,从r²的角度构建起方与圆的联系,并在思辨过程中培养了发散性思维。

