指向模型意识的评价框架建构与应用

【摘 要】乘法模型是基本运算模型之一。以人教版教材二年级上册“表内乘法（一）（二）”为例，指向模型意识的评价框架建构路径，通过实施“提炼核心内容目标，明确评价依据；细化表现性目标，厘清评价要素；划分水平层次，建构评价框架”等评价策略，探讨如何将指向模型意识的评价框架应用在教学的全过程中：课前，依据评价框架设计前测；课中，依据评价框架设计表现性任务；课后，依据评价框架设计基础性作业与表现性作业。

【关键词】模型意识；表现性评价；评价框架

《义务教育数学课程标准（2022年版）》（以下简称“2022年版课标”）明确指出：“数学课程要培养学生的核心素养。”在“学业质量”部分提出：“学业质量标准是以核心素养为主要维度，结合课程内容，对学生学业成就具体表现特征的整体刻画。”模型意识作为小学阶段核心素养中的具体表现之一，需要建构合适的评价框架，以观察模型意识的形成和发展。鉴于表现性评价更适合检测素养目标，且更有可能促进素养养成［1］。可以认为，对模型意识形成和发展的评价应当通过设计并实施表现性目标与表现性任务来进行。

在小学阶段，学生需学习一些具体的数学模型，这些模型按照难易程度可大致分为两类：第一类是加减乘除基本运算模型，注重运算意义的构建与应用；第二类是由基本运算模型组合而成的较复杂模型，强调在复杂情境中筛选、关联、指向与提炼信息［2］108。乘法模型作为基本运算模型之一，其意义的理解是数量关系学习的重要内容。在人教版教材中，乘法学习始于二年级上册，包括“表内乘法（一）”与“表内乘法（二）”两个单元，本文将其视为一个整体单元进行探讨。学习目标包括理解乘法意义、掌握表内乘法计算、解决生活实际问题，以及发展运算能力与模型意识。以下将聚焦于表内乘法单元，探讨指向模型意识的评价框架建构与应用。

一、建构指向模型意识的表现性评价框架

建构指向模型意识的表现性评价框架需要关注以下几点：一是确立表现性目标，表现性目标旨在描述学生需达成的基于学科素养的具体学习目标表现［2］109，这些目标应具备“可见、可评、可测”的特征。二是对学习目标具体表现进行整体刻画，以形成表现性评价框架。

（一）提炼核心内容目标，明确评价依据

制定表现性目标的第一步是根据模型意识确定相关学习内容，并结合模型意识的内涵与学业要求，提炼核心内容目标。2022年版课标指出：“模型意识主要是指对数学模型普适性的初步感悟。知道数学模型可以用来解决一类问题，是数学应用的基本途径；能够认识到现实生活中大量的问题都与数学有关，有意识地用数学的概念与方法予以解释。”人教版教材二年级上册的表内乘法教学，分为两个阶段：在学生对乘法意义有了深入理解后，先教学2～6的乘法口诀及相应的解决问题，随后再延伸至7～9的乘法口诀及相应的解决问题。

基于模型意识的内涵，按照“感悟模型—创建模型—应用模型”的认知路径，将模型意识划分为：感悟模型、使用数学模型表示现实情境、依托数学建模解决现实问题。根据表内乘法的教学内容与模型意识内涵维度，可以提炼出本单元的核心内容目标：（1）感悟乘法模型；（2）使用乘法模型表示现实情境；（3）依托乘法模型解决现实问题。

（二）细化表现性目标，厘清评价要素

核心内容目标是教学评价的内容和标准。在提炼出核心内容目标后，需进一步将其细化为表现性目标，以确保其易于实施与评价。将核心内容目标转化为表现性目标这一过程应紧密结合课标的要求与单元教学内容。

2022年版课标在第一学段“内容要求”中指出：“在简单的生活情境中，运用数和数的运算解决问题，能解释结果的实际意义。”在“学业要求”中指出：“能在熟悉的生活情境中运用数和数的运算，合理表达简单的数量关系，解决简单的问题。能在解决问题的过程中，体会解决问题的道理，解释计算结果的实际意义，感悟数学与现实世界的关联。”在“教学提示”中指出：“通过创设简单的情境，提出合适的问题，引导学生发现数量关系，利用画图、实物操作等方法，引导学生用学过的知识表达情境中的数量关系。”［7］基于上述分析，模型意识的形成和发展可具体表现为以下几个维度（如表1）。

（三）划分水平层次，建构评价框架

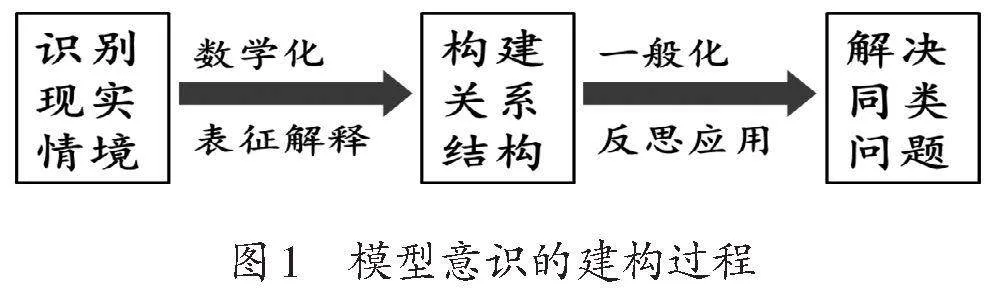
表现性目标需进一步转化为可操作的表现性水平层次，以便更精确地描述出学生核心素养的形成和发展情况。研究表明，模型意识的建构需要经历识别现实情境，在进行数学化后建构关系结构，经过一般化后用以解决同类问题［2］109（如图1）。

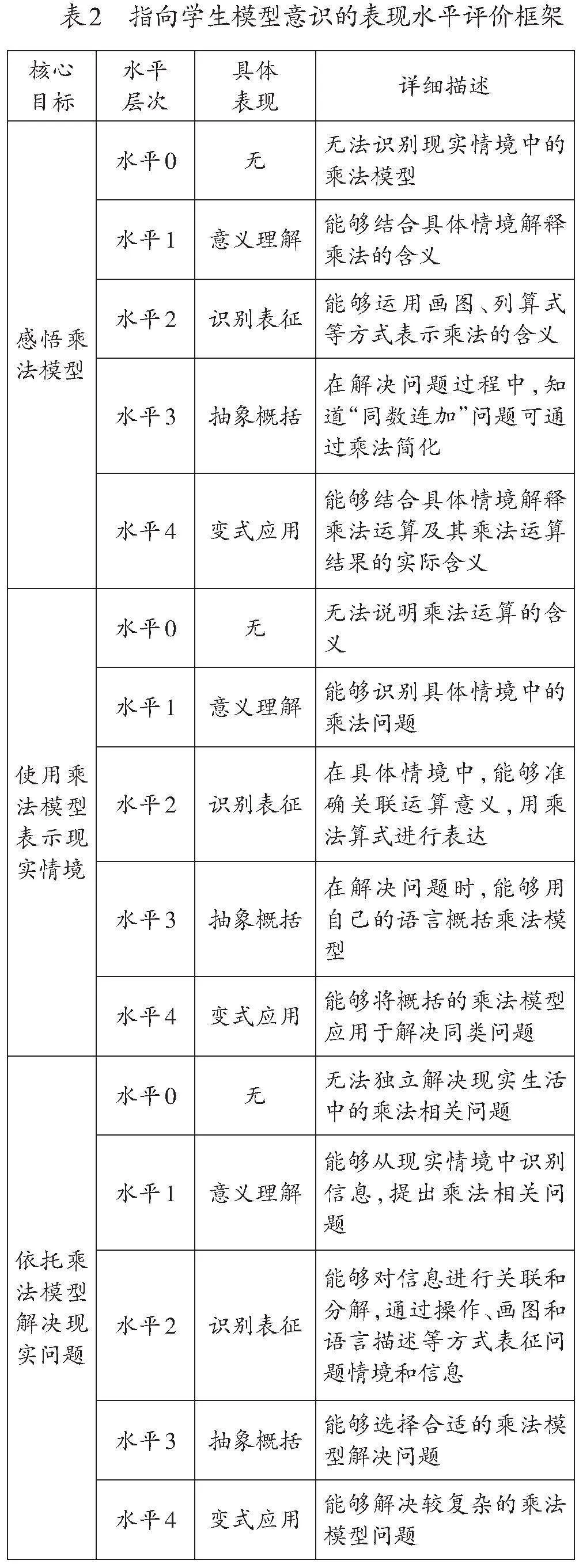
通常，模型意识的形成和发展需要经历四个步骤：（1）识别：从现实情境中识别信息，提出问题；（2）表征：通过操作、画图和语言描述等方式，将信息进行关联和分解，清晰呈现问题情境和信息；（3）抽象：将运算意义与现实情境相联系，用算式表达并解释抽象出模型；（4）概括：对建构的模型进行交流、验证和反思，并能运用到解决同类问题中。［2］109基于模型意识形成和发展的四个步骤，结合SOLO分类理论，将表现性目标根据学生的思维水平由低到高划分为五个水平层次，以此作为评价的基础和起点，建构起指向学生模型意识的表现性评价框架（如表2）。

二、表现性评价框架的实践应用

2022年版课标明确指出：“发挥评价的育人导向作用，坚持以评促学、以评促教。”简言之，课标强调评价学生的学习，以便教学能更有针对性地缩小学生学习现状与学习目标之间的差距，引领学生随着时间的推移，学习水平也随之提高［3］。在具体实践中，评价框架成为教师把握学生模型意识发展的程度、优化教学策略的重要工具，这一应用贯穿于课前、课中和课后的全过程。

（一）课前，依据评价框架设计前测

学生对乘法模型的感悟是其模型意识发展的基础。为此，教师对照乘法模型的评价框架设计前测，精准捕捉学生的学习起点，明确其当前模型意识的发展水平与目标之间的差距。

例如，通过设计如下的前测题，以了解学生能否识别以及会用何种方式表达现实情境中的乘法模型。前测题为：仔细观察这幅图，一共有多少小朋友坐火车？请你写一写，画一画，把想到的计算过程表达出来。

对二年级某班42名学生进行前测与访谈，结果显示：有33名学生使用加法来表示计算过程；有5名学生使用乘法表示计算过程；有2名学生采用“逐一计数”的方法；还有2名学生给出了错误结果。针对那5名运用乘法解决问题的学生，进行了访谈“你是怎么想到用乘法计算的？”其中，有4名学生的回答是：“每节车厢有6人，有4节车厢，即4个6，所以为4×6。”另1名学生能给出完整解释：“每节车厢有6人，因为有4节车厢，所以就是4个6相加，这也等同于4×6。”进一步访谈“你是如何得出4×6等于24的？”其中，4名学生直接用乘法口诀作出回答。而另1名学生则通过加法运算得出：“因为4个6加起来是24，所以4×6=24。”随后，访谈者要求这5名学生“用自己喜欢的方式表示3×2的含义”，结果是无人能够给出准确的表达。

通过此次前测，发现该班仅有约11.90%的学生达到了水平一，且那些能够写出乘法算式的学生，其乘法结构构建尚显薄弱。这为教师的教学提供了明确的方向：需加强学生从加法思维向乘法思维的转变，深化两者间的联系，并依托具体情境，通过画图、解决问题等活动，逐步提升学生的“感悟乘法模型”能力。

（二）课中，依据评价框架设计表现性任务

在教学活动实施的过程中，教师可依据模型意识的评价框架，设计一系列“低门槛、多层次、大空间”的表现性任务，具体如表3所示（以“使用乘法模型表示现实情境”维度为例）。在课堂上，教师应充分激发学生的主观能动性，鼓励他们进行多元化表征，并将学生的课堂生成转化为宝贵的学习资源，以此推动学生从模型意识的低水平逐渐向高水平进阶。

通过上述三个表现性任务，学生能够在“使用数学模型表示现实情境”维度，实现从水平一提升到水平四，有效促进模型意识的形成和发展。

（三）课后，依据评价框架设计基础性作业与表现性作业

作业体系本身既是一个复杂的整体，又是整个教育系统的一部分。作业是教学、评价关系的过渡与平衡支点，发挥着“过渡、平衡、支撑与协同作用”。［4］在教学实践中，教师可依据模型意识的评价框架，设计旨在巩固知识、技能的基础性作业，以此评价学生识别模型等认知水平的发展状况；同时，也可将表现性评价融入作业设计之中，通过表现性作业评价学生核心素养的发展水平。

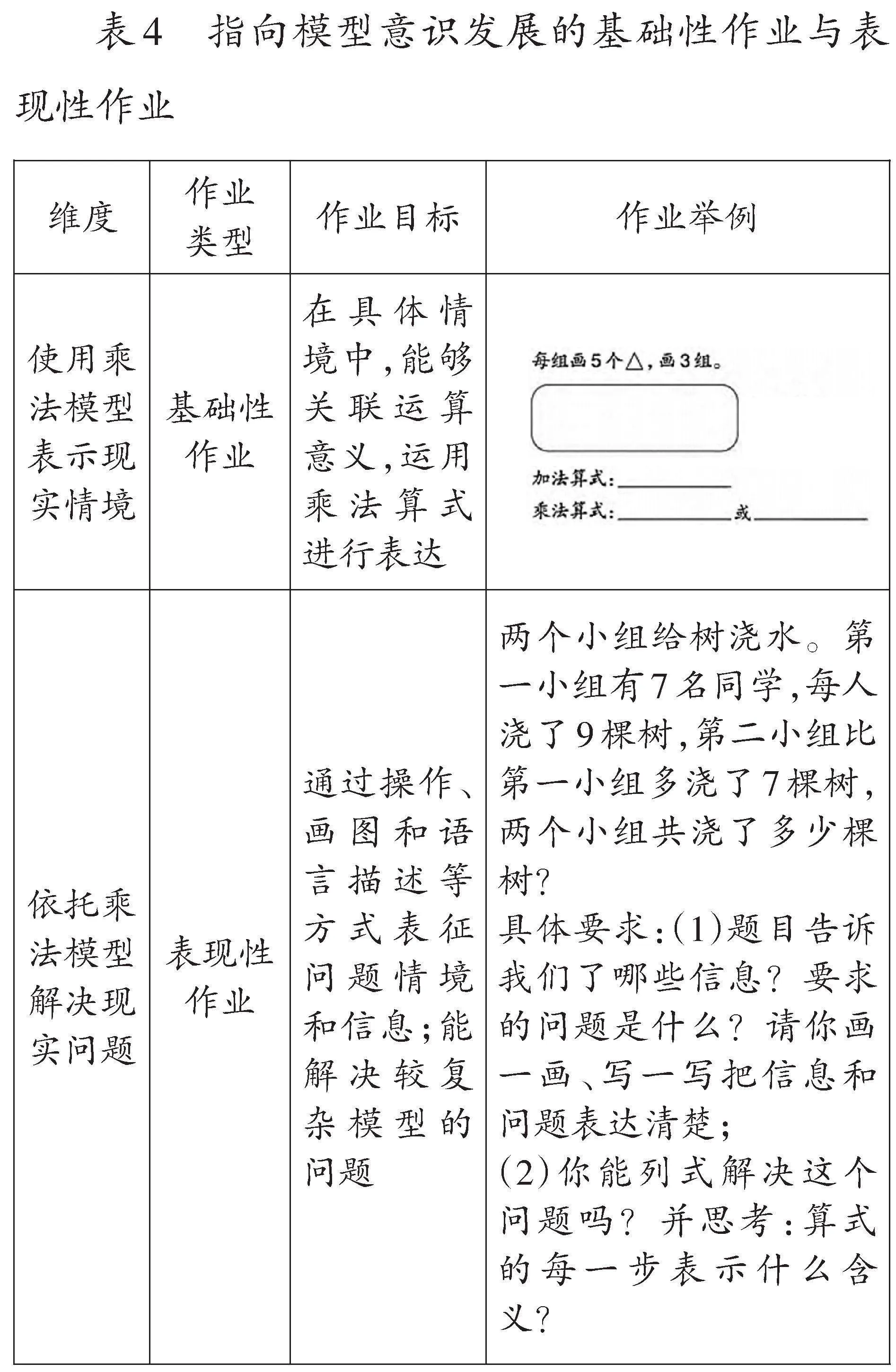
在设定作业目标时，应紧密围绕模型意识的各个维度，并结合具体表现进行精准定位。以下，笔者将分别举一例加以说明，具体如表4所示。

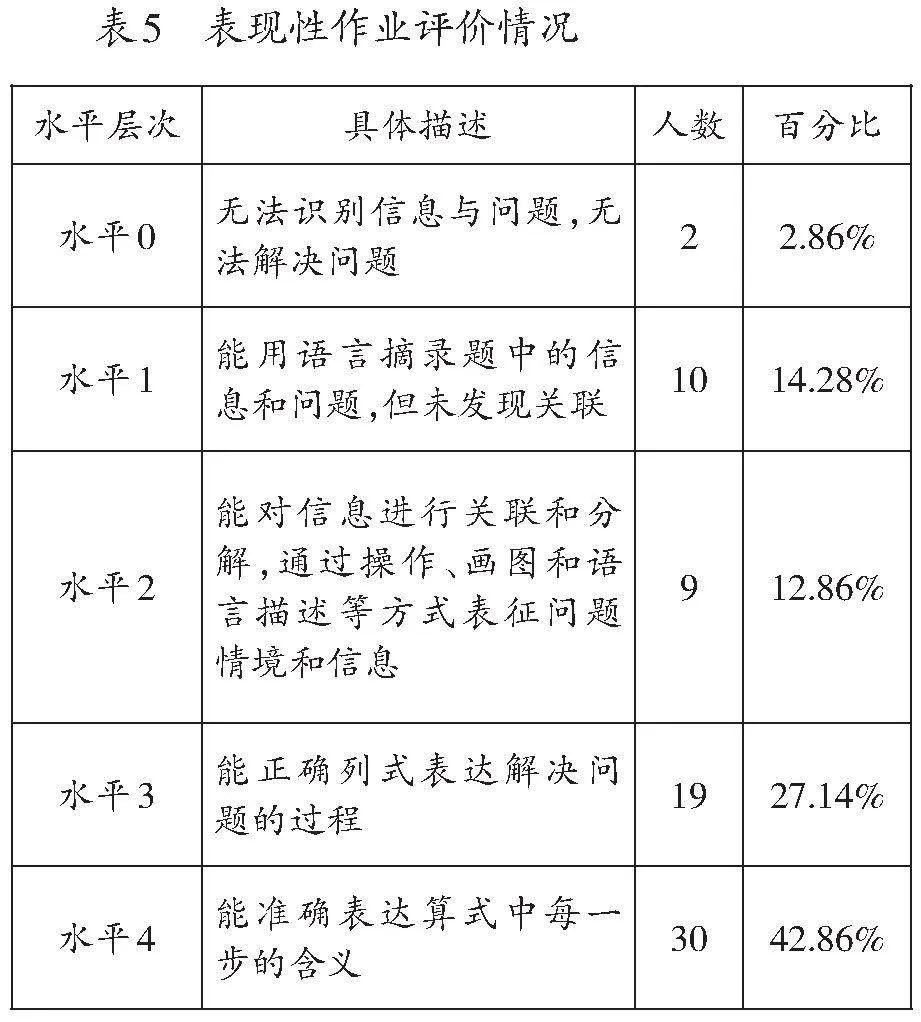
对表现性作业的评价，同样需要划分水平层次，以便深入观察学生的思维结构，揭示学生的潜在困惑，并据此提出切实可行的教学建议。对二年级70名同学完成表4中表现性作业的情况进行统计，具体结果如表5所示。

通过表现性作业评价情况，一方面可以评价学生模型意识的发展状况，另一方面也可以依据此情况进行作业的反馈与讲评。在讲评过程中，教师可先呈现水平1～水平2的作业，引导学生在对比中明确：仅仅摘录信息是不够的，还需对信息进行关联与分解才能有效解决问题。随后，教师可进一步呈现水平3的作业，通过讨论与对话，助力水平3的学生提升至水平4。

通过将这一指向模型意识的评价框架应用于教学实施的全过程，可全面评价学生的建模表现及模型意识的发展情况，并据此提出有针对性的教学建议，优化教师的教学策略，最终促进学生模型意识的形成与发展。

参考文献：

［1］曹培英，顾文.跨越断层，走出误区：小学数学深度学习教学研究［M］.上海：上海教育出版社，2022.

［2］章勤琼，陈肖颖.小学数学模型意识的内涵、表现与教学：兼论核心素养的表现性目标［J］.课程·教材·教法，2024，44（1）：106-113.

［3］范德沃尔，卡普，贝-威廉姆斯.美国中小学数学教师实践手册：第10版［M］.张晶，侯慧颖，施银燕，等译.上海：华东师范大学出版社，2023.

［4］王月芬.重构作业：课程视域下的单元作业［M］.北京：教育科学出版社，2021.