参数有界不确定下电磁分支电路阻尼优化研究

摘要：电磁分支电路阻尼器是一种轻量化振动控制手段。经典参数优化方法通常只适用于确定性参数模型，当系统参数发生变化时其抑振有效性可能会大大降低。考虑被控结构存在刚度有界不确定情况下，对串联型电阻-电感-电容电磁分支电路阻尼器进行最坏情况下的优化设计。采用一种改进型等峰优化设计代数方法，可以简洁地推导出分支电路电学参数最优值的近似解析表达式。最后，通过与经典等峰设计方法进行比较，验证了改进型参数优化设计在控制参数不确定性系统振幅的有效性。

关键词：电磁分支电路阻尼器参数有界不确定最坏情况最优化设计谐振分支电路

ResearchontheOptimizationofElectromagneticShuntDampingUnderUncertain-But-BoundedParameters

ZHOUShaoyiHUANGJungangCHENHuayinOUZijun

GuangzhouRailwayPolytechnic，Guangzhou，GuangdongProvince，511300China

Abstract：Electromagneticshuntdampingisalightweightapproachofvibrationcontrol.Classicparameteroptimizationmethodisusuallyapplicabletodeterministicparametermodels，possiblylosingitseffectivenesswhilethesystemparameterschange.Thearticleconsiderstheworst-caseoptimizationdesignofaseriesresistorinductorcapacitorelectromagneticshuntdampinginthepresenceofuncertain-but-boundedstiffnessinthecontrolledstructure.Animprovedmethodofequal-peakdesignis hereinadopted，withwhichonecouldconciselydeducttheapproximateanalyticalexpressionsofoptimalparametersoftheelectromagneticshunt.Finally，theeffectivenessofimprovedoptimaldesignincontrollingvibrationofuncertainsystemisvalidatedbycomparingwiththatofclassictuningstrategy.

KeyWords：Electromagneticshuntdamping;Uncertain-but-boundedparameter;Worst-caseoptimaldesign;Resonantshuntcircuit

在交通、机械、土木等众多工程领域中，可采用动力吸振器[1]来有效地限制主结构的机械振动。传统的动力吸振器是一种被动式减振装置，其由一个调谐质量块、弹簧元件和阻尼单元组成。动力吸振器最广泛采用的参数优化策略是等峰优化设计方法[2]，这种经验方法的形成是基于以下特殊现象，即无论吸振器阻尼水平如何变化，无阻尼主结构的频率响应曲线总是通过两个固定点。基于此，具有最优化参数的动力吸振器能够使得主系统频响曲线在两个固定点处的振动幅值相等且同时为频响曲线最高点。被动式动力吸振器的抑振性能可通过增大调谐质量、采用多个单自由度动力吸振器串联或并联在一起来增强。针对轻量化振动控制应用场景，电磁分支电路阻尼器[3]是传统动力吸振器的一种有效替代方式，可以有效解决质量和体积等物理限制条件。电磁分支电路阻尼器的核心元件是电磁换能器，它可实现系统机械能和电能之间的转换，从而可以通过与换能器外接的分支电路来消耗电能，进而减少系统的机械能。

ZHOUS等人[4]采用等峰优化方法推导了外接电容或电阻电容（RC）分支电路的最佳调谐参数。TANGX等人[5]系统地研究了串联或并联电阻电容分支电路的和参数优化问题，并推导出了参数的精确解表达式。PEIY等人[6]研究了耦合多个谐振分支电路的电磁分支电路阻尼器参数优化问题，并展示了其土木结构隔振的潜在应用前景。然而，上述研究都是基于确定性系统模型的假设，而在参数不确定性下对动力吸振器或电磁分支电路阻尼器进行优化设计研究仍鲜见报道。在实际工程应用中，由于测量不准确、制造公差和环境条件，结构参数或外部激励载荷可能存在参数不确定性。这些参数不确定性可由概率或非概率两种方式来进行描述。前一种方法是用由概率密度函数定义的高斯随机过程来表征参数不确定性。然而，当没有足够的实验数据来定义参数波动特性的概率密度函数时，这种方法无法提供可靠的准确性。在这种情况下，可以采用区间分析方式来定义参数不确定性，并假设参数在该区间内具有均匀的概率分布，称为参数有界不确定[7]。

本文采用串联型电阻-电容-电感（RLC）谐振电路的电磁分支电路阻尼器来控制单自由度无阻尼主结构的振动，研究主结构存在刚度有界不确定的情况下分支电路参数最优化问题。本文采用一种改进等峰优化方法，以更简洁有效地推导出分支电路的最优调谐参数。

1电磁分支电路阻尼器动力学模型

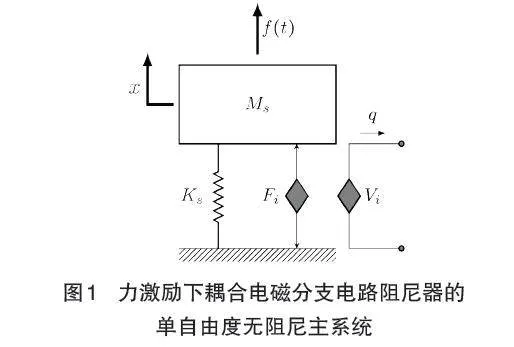
图1所示被控结构为单自由度质量-弹簧系统，控制其振动幅度的是由电磁换能器产生的反作用力（类似于传统动力吸振器产生的恢复力）。这个反作用力起到阻尼力的作用，与分支电路中电流大小成正比，即

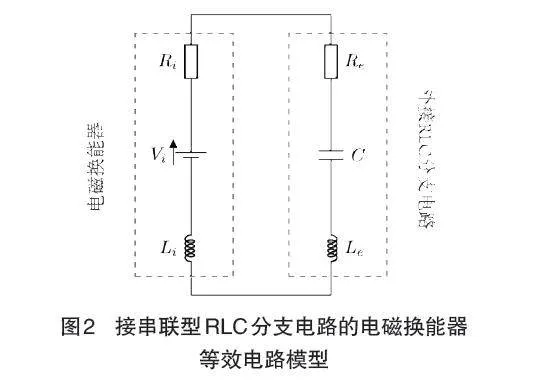
式（1）中，表示电磁换能器的机电耦合常数，是分支电路中的电荷，符号上点表示相对于时间的微分。图2为外接串联型RLC分支电路的电磁换能器的等效电路模型，其中和分别为电磁换能器的内电感和内电阻，为等效受速度控制电压源。现考虑主结构受到正弦力激励的情况，则图1所示机电耦合系统的运动方程可描述为

式（2）中，是等效质量，是机械刚度，表示分支电路电容值。此外，和分别代表分支电路中的总电阻和总电感。最后，下标指代实际的系统参数。

分别用和表示位移和外界激励力的复幅值，通过对式（2）进行拉普拉斯变换可获得主系统位移的频率响应函数。

式（3）中，为复变量（），为外部激励频率。通过分子和分母同时除以，并定义无量纲复变量为，主系统位移频率响应函数可变换为

下标表示主结构的名义系统参数，如和，而表示主系统的名义固有频率。

1.1确定性模型

在能量采集和振动控制领域，确定性模型被广泛用于预测系统的动力学响应。在本研究中，当假设主系统是确定性的，即系统参数中不存在不确定性时，有和，然后可以将先前的位移频响函数简化为

式（5）中，是由针对系统静位移进行归一化的无量纲主系统位移的拉普拉斯变换。其幅值平方大小可以表示为：

式（6）中，系统常数和无量纲参数定义如下：

式（7）中，表示主系统名义固有频率，是分支电路谐振频率，是电路阻尼比，表示电磁耦合系数。此外，表示无量纲外界激励频率，表示频率调谐比。待优化的分支电路参数为频率调谐比和电路阻尼比。

1.2有界不确定性模型

由于各种因素，如材料退化和环境变化，系统机械参数可能存在不确定性。因此，根据经典等峰优化方法调谐的吸振器可能由于系统参数的失谐而失去抑振能力，甚至可能出现加剧被控结构的振动情况。本文中主系统的机械刚度是有界不确定的，可以用这样一个区间变量来描述：

式（8）中，上标I代指区间变量，和分别表示区间变量的下界限值和上界限值。本项研究中刚度区间变量被认为是对称的，其中间值即为系统名义刚度，因此也可以表示为

式（9）中，表示刚度最大不确定度；则是一个随机变量，用于量化实际机械刚度与其名义值的偏差程度，其在整个区间内概率分布是均匀的。因此，主系统存在刚度有界不确定情况下，其位移频响曲线幅值平方的表达式可表述为

式（10）中，为中间变量，其他符号表达式分别为

因此，不确定系统的动力学响应由强迫频率、频率调谐比、电阻尼比和实际刚度不确定性控制，即。

1.3有界不确定性下参数最优化

针对系统参数有界不确定情况，本文采用一种改进型等峰优化方法进行参数优化，该方法旨在使得主系统在最差情况下所能达到的最左侧共振峰（即）与其在最右侧所能达到的共振峰（即）具有相同的幅值。该方法可通过以下公式来表示。

为节省篇幅，本文中分支电路优化参数推导过程予以省略。经分析，分支电路最优频率调谐比表达式为

式（14）中，。很容易证明，当系统刚度等于其名义刚度值（即）时，本文所求出的最优频率比及阻尼比值与文献中采用经典等峰优化方法得到的最优值完全一致，验证了本文所提出的刚度有界不确定情况下参数优化设计的准确性。

2数值仿真分析

本文中算例模型参数分别为：主系统等效质量，刚度，电磁换能器内电阻，内电感，电磁耦合系数。

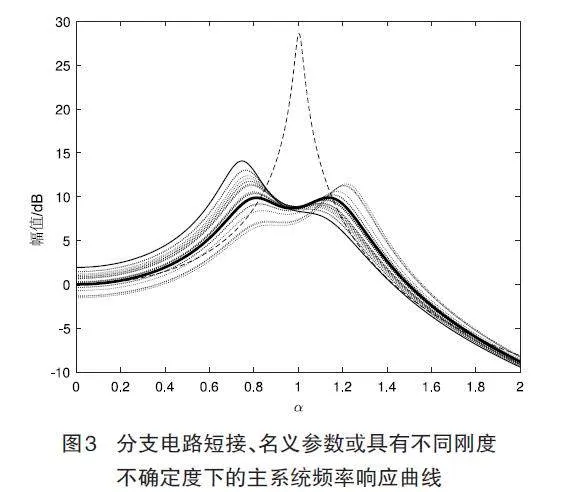
图3展示了耦合串联RLC分支电路阻尼器的主系统位移频率响应曲线。虚线表示阻尼器直接短接情况下具有名义参数的主系统动力学响应。粗实线对应名义参数情况下的最优设计动力学响应。20条圆点虚线则对应不同不确定度下的频率响应曲线（在[-β，+β]区间随机抽取20个刚度不确定度值），细实线代表最坏情况下的频响曲线。结果表明，与电磁换能器直接短接情况相比，采用经典等峰方法调谐的阻尼器在具有名义参数情况下可将主体结构的振动幅度降低18.7dB；而在考虑20%刚度不确定度的最坏情况下，仅可将振动幅度降低14.6dB。也就是说，由于失谐，机械系统的振动比名义参数情况下恶化60%，从而更加突出考虑参数不确定性下重新优化分支电路参数的重要性。

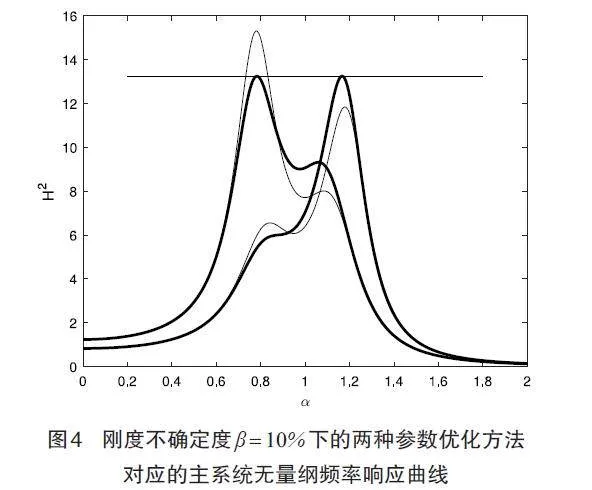
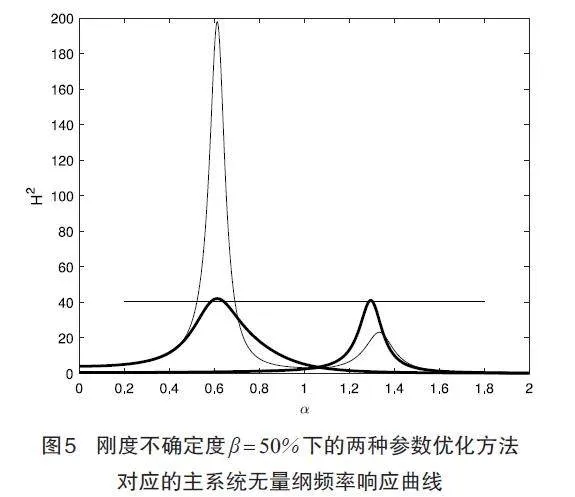
图4和图5分别展示了刚度最大不确定度和情况下采用不同优化设计方法下的耦合系统针对系统静位移进行归一化的无量纲位移频响曲线。细实线表示通过经典等峰方法调谐系统参数的振动响应，粗实线则对应改进型等峰优化方法。从图4和图5中均可以看到，无论最大不确定度大小如何，本文中采用的改进型等峰优化方法可以均衡主系统在两种最坏情况（最低和最高频率）下的振动幅值，并使最坏情况下的峰值最小化且基本等高。当最大不确定度为10%时，改进型等峰方法设计的分支电路阻尼器能比经典方法优化的阻尼器再降低13.5%的振幅；而当最大不确定度上升至50%时，改进型等峰方法的优势进一步得到体现，此时可比经典调谐方法再降低78.8%的振幅。

3结语

本文研究了考虑主结构刚度有界不确定情况下串联型RLC电磁分支电路阻尼器的参数优化问题，并采用一种改进型等峰优化代数方法，可以更简洁、有效地推导出分支电路参数最优值的解析公式。与经典的等峰优化方法相比，本文所采用的改进调谐方法可以在整个不确定度范围内更有效地控制主结构的机械振动。数值仿真结果表明，考虑最大不确定度达到50%的极端情况下时，相对于经典设计，改进参数优化设计可以进一步降低主结构在最坏情况高达78.8%的振幅。

参考文献

[1]张明华，杨国庆，杨毅青，等.内置动力吸振器的宽频减振车刀设计及试验[J].振动与冲击，2023，42（18）：338-344.

[2]杨晓彤，申永军，王俊锋.一种含放大机构、惯容和接地刚度的动力吸振器的参数优化[J].振动与冲击，2022，41（21）：308-315.

[3]ZHOUS，BAOB.Investigationonhigh‐orderresonantelectromagneticshuntdampersforvibrationcontrol：Methodologyandoptimumtuning[J].StructuralControlandHealthMonitoring，2022，29（11）：e3094.

[4]ZHOUS，JEAN-MISTRALC，CHESNES.Electromagneticshuntdampingwithnegativeimpedances：optimizationandanalysis[J].Journalofsoundandvibration，2019，445：188-203.

[5]TANGX，LIUY，CUIW，etal.AnalyticalsolutionstoH2andH∞optimizationsofresonantshuntedelectromagnetictunedmassdamperandvibrationenergyharvester[J].JournalofVibrationandAcoustics，2016，138（1）：011018.

[6]PEIY，LIUY，ZUOL.Multi-resonantelectromagneticshuntinbaseisolationforvibrationdampingandenergyharvesting[J].JournalofSoundandVibration，2019，423：1-17.

[7]杨振宝.具有有界不确定参数的FG-GPLRC板的强迫振动分析[D].广州：广州大学，2020.