借助大概念，在运算教学中促进学生思考

“分数乘法（三）”是北师大版教材五年级下册的内容，是在分数乘整数的基础上学习分数乘分数，这是“分数乘法”单元的重点和难点内容。学生虽然已经具备丰富的分数加减法及分数乘整数的经验，但考虑到分数乘法的抽象性和学生偏重于形象思维这一特点，本课需要借助大概念统整单元教学框架，利用面积模型探索算理，归纳算法，从而促进学生思考，体会运算的一致性，发展运算能力。

一、创设情境，提出问题，理解意义

师：同学们，你们知道庄子吗？他是我国古代著名的哲学家。这有一则与庄子有关的资料，同学们自己读一读吧。

出示资料，（如图1）学生自由阅读。

师：想一想，你同意“一尺之棰，日取其半，万世不竭”这个观点吗？谁来说一说自己的想法？

生1：我不同意，每天截一半，两天就截完了呀！

生2：我同意，因为第一天截去一半，还剩下一半；第二天还是截去一半，还剩下一半；可以一直截下去啊。

生1：我明白了，第二天截下去的是一半的一半，还剩下一半的一半，的确截不完。

师：同学们独立思考，交流讨论，弄清了这段话的道理，真好！原来，每次截“一半”会剩下“一半”，再继续截，仍会剩下“一半”，只不过这些“一半”不都是一样长的。我们用一张纸条表示这根木棍，那么每次取一半之后，剩下的部分占这张纸条的几分之几呢？

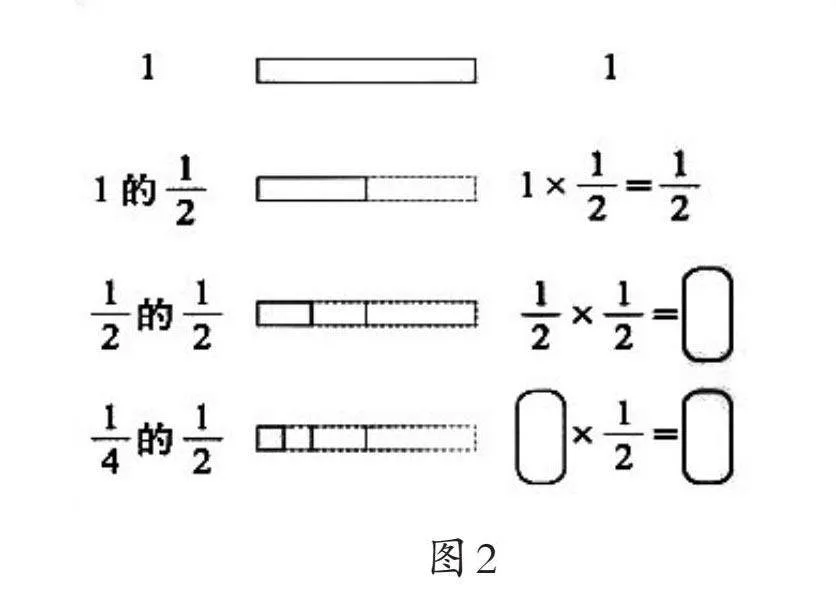
学生再次阅读资料，对应直观图，（如图2）理解每个算式的意思，完成填空，并解决上述问题。然后，请一名学生到黑板前分享。

生3：（手势配合）这是一张纸条，用1表示；第一天截去一半，剩下一半，是1的[12]，也就是1×[12]=[12]；第二天又截去剩下这一半的一半，结果剩下这张纸条一半的一半，是[12]的[12]，也就是[12]×[12]=[14]；第三天再截去剩下这[14]的一半，结果剩下这张纸条[14]的一半，是[14]的[12]，也就是[14]×[12]=[18]；依次类推……

师：在前两节课，我们已经学习了分数乘整数，这节继续学习分数乘法（三）——分数乘分数。［板书课题：分数乘法（三）——分数乘分数］

师：同学们都知道，学习有关运算的内容时，主要应弄清两点：一是运算的意义，二是运算方法。谁能结合图示再来说一说，这里的 [12]×[12]=[14]、[14]×[12]=[18]各表示什么意思？

生4：[12]×[12]=[14]表示[12]的[12]是[14]，[14]×[12]=[18]表示[14]的[12]是[18]。

生5：和上节课学过的3×[34]表示3的[34]是多少的意义一致，分数乘分数也是求一个数的几分之几是多少。

师：借助这个问题，我们知道了分数乘分数运算的意义。但是计算方法呢？

生：分母相乘，分子不变。

生：不对吧？应该是“分子相乘作分子，分母相乘作分母”。

生：这几个分数都是分数单位，你俩说得都对。

师：（顺势板书“分子相乘作分子，分母相乘作分母”）这种方法是否正确？背后又有什么道理呢？特殊的分数不具有一般性，并且这个结果我们是可以从图中看出来的。接下来，我们以[34]×[14]为例，重点研究分数乘分数的运算方法。

【设计意图】首先，通过在情境中阅读以及学生的辨析，理解“一尺之棰，日取其半，万世不竭”的意思，达成共识，体会其中精深而有趣的数学现象。接着再次阅读教材，在阅读中思考和理解直观图所蕴含的意义及算式所表达的意义，培养学生的数学阅读理解能力。最后，引出课题，初步理解分数乘分数的意义。

二、探索分享，明晰算理，总结算法

1.独立思考，想一想，说一说。

师：[34]×[14]表示什么？你想怎么计算呢？

学生独立思考，然后交流想法。

生1：[34]×[14]表示[34]的[14]是多少，可以先把一张纸平均分成4份，涂出其中的3份，就表示出了[34]。可是接下来，我不知道怎么做了。

师：先给你点个赞！能从解决上一个问题的方法中得到启示，想到用纸折一折、涂一涂，很好。而且，你们对分数的意义理解得很好，能轻松地找到[34]。那怎样表示[34]的[14]呢？

2.动手操作，折一折，涂一涂。

师：请同学们拿出一张长方形纸，先想一想怎样折，想清楚的同学动手做一做，然后在小组内说说你的操作过程。

学生思考后，动手操作。教师巡视，了解整体探索情况。

3.交流分享，看一看，说一说。

学生在小组内分享，初步了解不同的方法，教师巡视，同时帮助学习有困难的学生。

师：下面请想到不同方法的同学进行分享，如果有补充或质疑，请在汇报结束时提出来。

生1：我是这样做的，先把这张纸“十”字对折，平均分成4份，涂出其中的3份，表示[34]。再继续“十”字对折，把每1大份平均分成4小份，这样就把整张纸平均分成了16小份，再涂出涂色部分每1大份的[14]，即1小份，这样就涂出了3小份，占整张纸的[316]。（如图3）

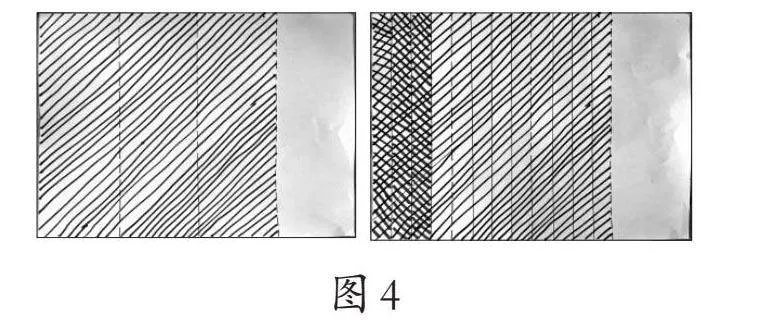
生2：我是这样做的，先把这张纸对折两次，平均分成4份，涂出其中的3份，表示[34]。再把涂色部分继续对折两次，把每1大份平均分成4小份，这样就把涂色部分平均分成了12小份，再涂出涂色部分的[14]，这样就涂出了3小份，占[316]。（如图4）

生3：（质疑）从你画的图上看，最后涂色的部分应该是[312]呀！（看着台上、台下同学都开始思考，他接着说）你把右边空白部分也得平均分成4份，这样总份数就是16份了，涂色部分就是整张纸的[316]。

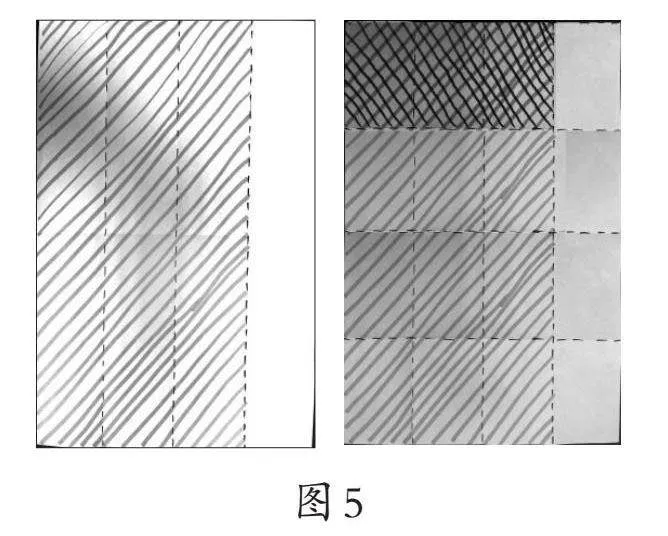
生4：我和生2第一次的分法相同，都是先把这张纸竖着对折两次，平均分成4份，涂出其中的3份，表示[34]。接下来，我换了一个方向，把这张纸横着对折两次，再次平均分成4份，涂出涂色部分的[14]，就是3小份。整张纸被平均分成了16小份，最后涂出的是整张纸的[316]。（如图5）

师：观摩了这几位同学的分享，你们有什么想法？这几种方法有什么联系吗？

生5：我发现他们都是分了两次，先平均分成4份，再平均分成4份，最后都是平均分成了16份。

生6：我喜欢第三种折法，换个方向折，能更清楚地表示计算过程，也更容易看出计算结果。

师：好的，那咱们一起再来折一折，思考两次折叠和两次涂色的作用是什么。

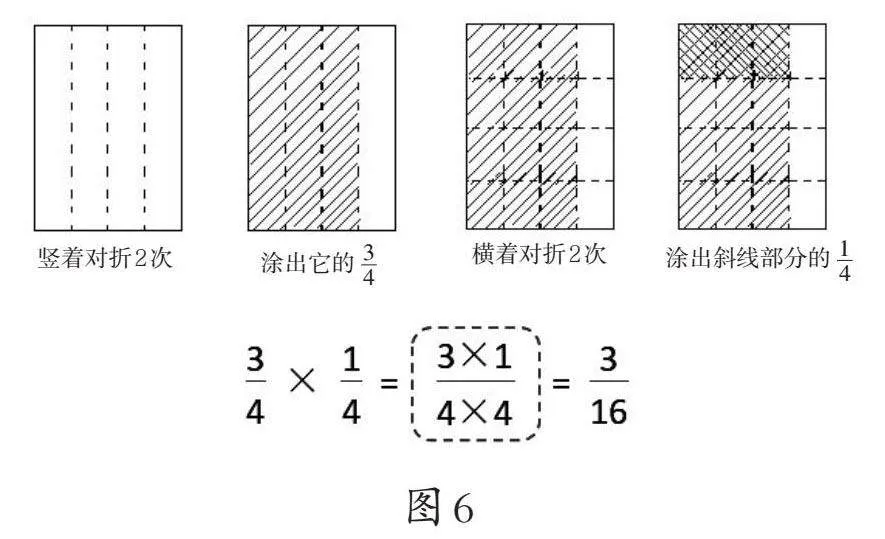
全体学生动手折一折，教师再次组织学生交流分享，并板贴记录折纸过程及计算过程。（如图6）

生7：我知道了，两次折叠得到的是新的分数单位，即确定分母；两次涂色得到的是新的分子。

生8：分数乘分数的计算方法就是分子乘分子、分母乘分母。

4.总结方法，沟通联系。

师：同学们得出的计算方法是否正确呢？需要验证一下。结合下面的题目（如图7）折一折、算一算、说一说吧。

学生可以先折再算，也可以先算再折，验证得出的计算方法。交流中完善算法：能约分的可以先约分。

师：想一想，分数乘整数的计算方法（分母不变，分子与整数相乘）与分数乘分数的计算方法有什么关系？

生1：其实，分数乘分数计算的道理与分数乘整数是一样的，都是先确定分数单位，然后乘个数，得出结果。

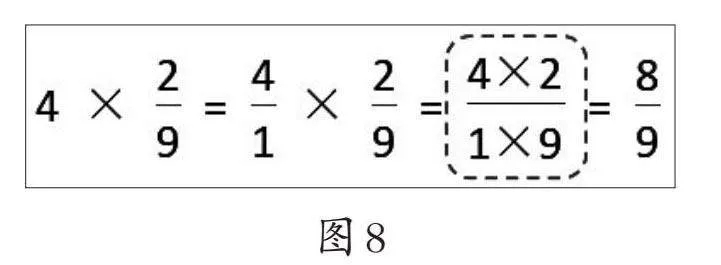
生2：整数就是分母是1的分数，例如4×[29]可以看成[41]×[29]，分母相乘还是9，分子相乘是8，因此结果就是[89]。（如图8）

生：我来总结。无论是整数、小数还是分数，在乘法运算时，都是先确定计数单位，然后乘个数，从而得出结果。

师：你真了不起！不但弄清楚了分数乘法的意义与运算方法，还发现了整个乘法运算的共同之处，给你点赞！

【设计意图】借助运算教学大概念，从乘法的意义与分数的意义出发，整体思考，贯通运算教学结构，明确了分数乘分数的意义。通过折纸活动，借助面积模型的直观，理解了“分子相乘、分母相乘”的运算方法，并与分数乘整数、小数乘法、整数乘法沟通联系，体会运算的一致性。

算法什么时机总结更合适呢？第一次执教时，我尊重教材的编排顺序，带领学生先借助折纸研究[34]×[14]，在大部分学生都有充分的体验后，水到渠成地进行运算方法的提炼和总结。学生很顺利地提出了“分子相乘作分子，分母相乘作分母”，但当问到“为什么要分子、分母分别相乘”时，几乎没有学生能答得出来。

本次执教时，我没有急着进行折纸探究，而是结合一名学生“提早”提出的方法，顺势板书“分子相乘作分子，分母相乘作分母”的计算方法。接下来完全放手，学生研究的方向更明确，思考时也有一定的“阶梯”，在分享交流时，学生也更易“数形结合”“指向本质”。

是不是所有的运算教学都要先提出方法，再进行算理的研究呢？事实上，方法提出的时机可以不同，只要是顺应学生的思维路径，顺势而为，根据学生实际情况来决定就好。如果学生先提出了，不能置之不理，那么接下来的任务就应该是弄清方法背后蕴含的算理；如果学生没有提出，那就结合折一折、涂一涂、算一算等活动让学生体会运算的道理，然后在此基础上总结计算方法。

（作者单位：黑龙江大庆市第六十九中学二部） J