变与不变：“平行四边形面积”教学的新探索

一、学前测试及分析

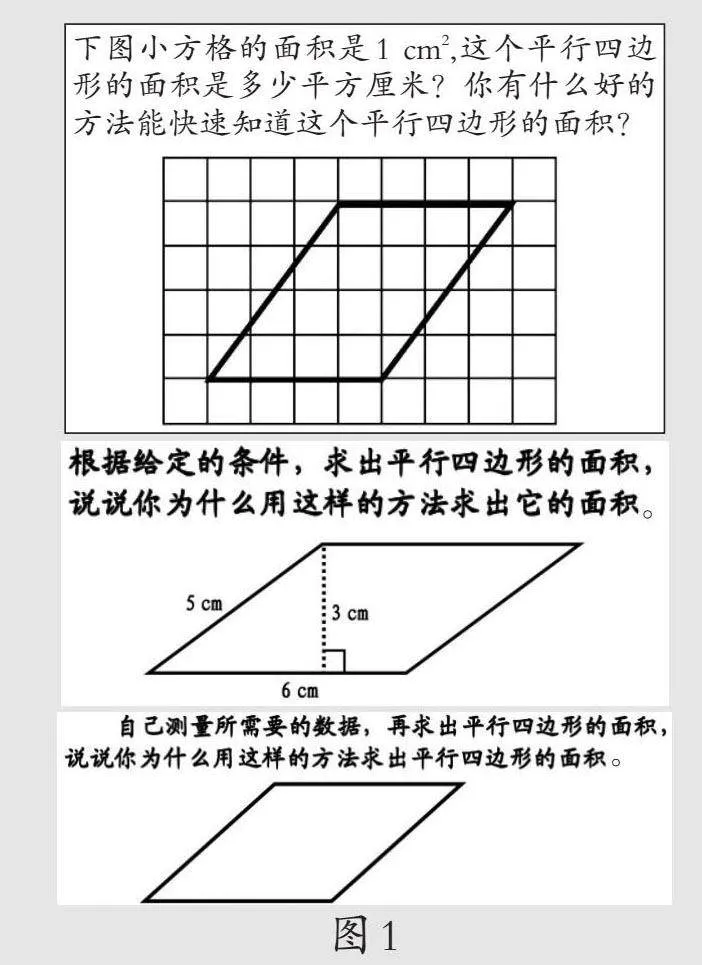
五年级学生在学习平行四边形面积之前基本掌握了平面图形的特征，明确了面积的意义，经历了长方形面积计算公式的推导过程，积累了一定的动手操作能力和推理意识。在推导过程中，基本掌握了通过数格子（1 cm2）等方法可以得出图形的面积。但之后一年多较少涉及面积知识，学生的基础怎样？他们对转化思想的理解力如何？有必要开展一个知识前测便于准确把握学情。笔者设计了3个题目（如图1），分别在城镇小学3个同质学生平行班进行调查，调查时间为教学此内容前10天，要求在5分钟内独立完成。调查结果如表1所示。

这3个班级的学生分别对不同要求、不同思维层次的题目进行解答，可以从一个侧面了解平行四边形面积前概念情况。从调查的结果看，大部分学生不借助方格图也能通过自己的测量求出平行四边形的面积（约占77.3%），且理由写得比较正确。在题1中可以发现，约83.7%的学生采用整体切割的方法进行拼组，明显区别于教材中“不满一格都按半格算”这样数一数的方法；而在题2、题3中，大部分学生也通过整体剪拼变成长方形然后求出平行四边形的面积。因此，笔者认为：一是教学时可以组织学生动手实践或借助方格图引导其自主探究平行四边形面积，再比较两种方法的相同点，从而渗透转化思想，感受形状变了而面积不变的本质。

二是根据学生基础较好的实际，可以把平行四边形的面积研究得更深入一些，进行周长变了面积不变、面积变了周长不变的练习，渗透“变中有不变”的辩证思想。

二、课堂教学实践

环节一：迁移已有经验，引发认知冲突。

课始，出示一个平行四边形，设疑：这是一个平行四边形，你已经知道了它的哪些知识？还想知道关于它的哪些知识？通过答疑，学生想研究平行四边形的周长和面积。于是，教师给定平行四边形的底边和邻边的长度分别是6 cm和5 cm，学生快速口答它的周长是22 cm。随后，猜测这个平行四边形的面积是多少。

生：平行四边形的面积是6×5=30（cm2）。

生：不对，这个5 cm不是它的高，要求出平行四边形的面积，需要知道高是多少。

师：如果这个高是4 cm，面积是多少呢？

生：6×4=24（cm2）。

针对两种不同的答案，组织学生采用方格图和其他学具进行验证。我们认为，这个环节一是可以调动学生已有的认识图形经验，自然地引出求平行四边形的周长和面积这两个知识点，引导学生用熟悉的方法进行计算，无形中促进图形间知识的迁移；二是在求平行四边形的面积时，学生有认知冲突，出现了“底边×邻边”和“底×高”两种方法，引发学生进一步思考；三是借助具象的平行四边形图和方格图，让学生经历由猜想到验证的过程，培养他们的动手操作能力和推理意识。

环节二：借助生成资源，推导面积计算公式。

根据课前调查的情况和提供的学具，学生一般会研究出两种不同的推导思路，可以对这两种方法进行对比与分析。在研究的基础上集中反馈。

反馈一：

生：平行四边形的面积是24 cm2。我是用数格子的方法，先数满格的，有18格，再把不满格的拼在一起，拼成6格，一共是24格，面积就是24 cm2。

生：我是这样数的，把左边多的这块拼到右边，然后数一数每行的格数，再数有几行，然后算一算，总共是24 cm2（如图2）。

然后让其他学生说说第二位同学在数的时候采用的方法，得出整体切割、平移、拼组的方法，采用“每行个数×行数=总个数”的方法来计算面积。

反馈二：

生：我是把这个平行四边形沿着高剪开，再把它拼成一个长6 cm、宽4 cm的长方形，长方形的面积是24 cm2，平行四边形的面积也就是24 cm2。

师：在这个剪拼的过程中你们发现了什么？

生：在剪拼的过程中，平行四边形变成了长方形，形状变了，但是面积不变。长方形的长就是平行四边形的底，宽就是平行四边形的高。

师：两种方法都验证了它的面积是24 cm2，也就是底的单位面积个数×高的单位面积个数，这就是平行四边形的面积。那数方格法和剪拼法这两种方法之间有联系吗？

生：它们都是将左边多出来的部分移到右边，把平行四边形剪拼成了一个长方形，但面积不变。这样，不仅数起来简单，计算起来也简单。

师：是的，这两种方法背后的道理是一样的，都用到了“转化”的方法。通过比较、沟通和联系，现在我们知道平行四边形的面积=底×高（如图3）。

随后，组织学生进行两个平行四边形面积的计算，在计算的过程中掌握字母公式和底与高相对应的知识点。

这一环节主要问题是在对比中发现整体数方格的方法与剪拼法本质上是一致的，都是基于对规则图形的度量，同时第一次让学生感受平行四边形面积计算公式推导过程中的“变与不变”。

环节三：利用框架演示，感知变与不变。

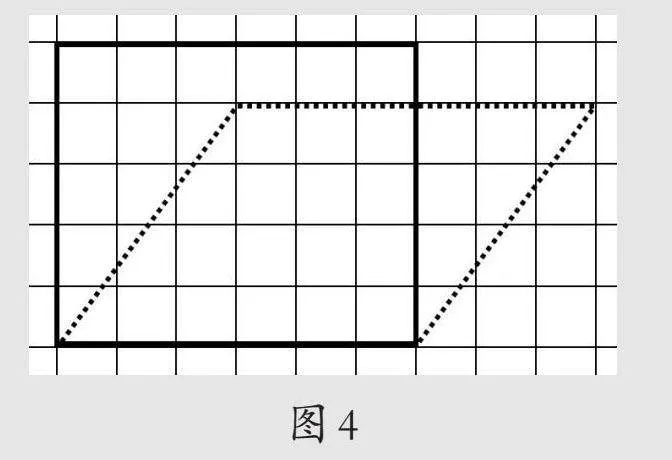
在课开始时，学生猜想出面积是6×5=30（cm2），他们的认知困惑在哪里？教学的生长点又在哪里？教师需要利用这一生成性资源进行拓展。接着设疑：想象一下面积是6×5=30（cm2），这是在计算怎样一个图形的面积？组织学生利用框架进行演示：将平行四边形拉成长方形（如图4）。

师：观察刚才的图形和现在的图形，你有什么发现？

生：我发现形状变了，由平行四边形变成了一个长方形。

生：我发现周长不变，面积发生了变化，面积比原来更大了。

师：如果这个图形的周长不变，面积会发生变化吗？为什么？

生：面积会发生变化，因为高一直在变。

师：在这个变化过程中，什么时候面积最大？什么时候又变小？你有什么想法？

生：当拉成长方形时面积最大，因为这个时候高等于长方形的宽，是最大的时候；再拉动时，面积又变小了，因为高变小了。

生：我觉得平行四边形的面积变化与高的变化密切相关。

这是第二次让学生感受“变与不变”的规律，也就是周长不变，面积发生变化，其本质是小学阶段平行四边形面积与邻边的长度没有直接联系，而与高有密切的关系。

随后，组织学生研究面积是24 cm2的平行四边形还会有怎样的形状，也就是等底等高的平行四边形（面积相等的图形）会有怎样的特征。设问：如果平行四边形的底是6 cm、高是4 cm、面积是24 cm2，还能画出其他的平行四边形吗？独立完成后鼓励学生上台展示所画的平行四边形。

师：这些平行四边形的面积是多少？你是怎么判断的？

生：面积都是24 cm2，因为它们都可以转化为长6 cm、宽4 cm的长方形。

生：这些平行四边形的底都是6 cm、高都是4 cm，底和高没有发生变化，所以它们的面积不变，还是24 cm2。

师：刚刚大家所画的平行四边形和老师一开始出示的平行四边形有什么关系？

生：它们面积不变，但形状变了，周长变了。

生：我发现底与邻边的夹角发生了变化，高不变，面积不变，周长变了。

师：像这样，底是6 cm、高是4 cm、面积是24 cm2的平行四边形有多少个？

生：有无数个。只要所画的平行四边形底是6 cm、高是4 cm，无论形状怎么变，夹角怎么变，它们的面积始终是24 cm2。

……

学生通过想象、观察和动手操作，深刻感悟到“面积不变，角度、周长变了”，渗透了“变与不变”的内涵，也为初中研究平行四边形面积与邻边的关系埋下了伏笔。

借助具象的框架演示，有利于减轻学生的认知负担，在有限的时间内使研究开展得更深入。活动紧紧围绕两条线开展：一条线是“周长不变、面积发生变化”，另一条线是“面积不变、周长发生变化”。这一过程中学生灵活运用转化思想，推导出平行四边形的面积计算公式，在“变”与“不变”中，加深了对知识的理解，把平行四边形的面积顺利纳入图形面积的整体结构中。

（作者单位：浙江桐庐县方埠小学） L