一种消除椒盐噪声的迭代自适应加权均值滤波

文章编号： 1006-9798（2024）03-0039-07； DOI： 10.13306/j.1006-9798.2024.03.006

摘要： 针对传统的均值滤波和多种中值滤波不能有效去除高密度椒盐噪声的不足，提出一种迭代自适应加权均值滤波算法。为了能够对图像外围的像素点进行滤波，沿四周进行图像扩展。根据椒盐噪声的极值特性，将像素点分为噪声点和信号点，噪声点采用多轮迭代，利用前次滤波的结果，求取滤波窗口非噪声点灰度值的加权均值，基于与窗口中心像素的空间距离计算加权系数；信号点保持原值。滤波窗口尺寸根据窗口内是否含有非噪声点自适应地由小变大。选用5种不同的算法在噪声密度20%～80%范围内进行仿真对比，验证算法的有效性。仿真结果表明，与其它4种算法相比，在低密度噪声时，该算法的峰值信噪比（Peak SignaltoNoise Ratio，PSNR）和结构相似性指数（Structural Similarity Index，SSIM）优势明显，在80%高密度噪声时仍然保持突出效果，PSNR值至少提高4.26 dB，验证了该算法对高密度椒盐噪声具有更好的滤波性能，很好地保持图像的纹理边缘和细节。

关键词： 椒盐噪声； 图像扩展； 均值滤波； 中值滤波； 迭代自适应加权均值滤波

中图分类号： TP3文献标识码： A

椒盐噪声是一种常见的固定值脉冲噪声，就像椒盐一样，被污染的像素变为最小灰度值或最大灰度值，图像中随机出现黑点（胡椒点）或白点（盐点）的像素。均值滤波（Mean Filtering， MF）是常见的图像滤波算法，它将每个像素的值替换为滤波窗口像素的平均值，很好地平滑高斯噪声，但对椒盐噪声的效果较差，容易损失图像的细节信息，使图像变模糊。标准中值滤波（Standard Median Filtering， SMF）[1]是去除椒盐噪声最常用的算法之一，该算法处理低密度噪声时滤波效果良好，但对于高密度噪声效果较差。为了解决降噪和保留细节的矛盾问题，许多学者提出改进的滤波算法。自适应中值滤波（Adaptive Median Filtering， AMF）[2-3]增加了对噪声点的判断，可动态改变滤波窗口的尺寸，在高密度椒盐噪声情况下，对图像细节保护能力有限，会残留一定的噪声。加权均值[4-5]、加权中值滤波[6]、方向中值滤波[7]、迭代中值滤波[8-11]、自适应模糊中值滤波（Adaptive Fuzzy Median Filtering， AFMF）[12-13]等算法也相继被提出。其中，AFMF采用极值法检测噪声，通过模糊规则对疑似噪声点是否为噪声进行模糊分类，噪声去除时，信号点保+0eilKZlOvzwRFDyjp1yyA==持原值输出，疑似噪声点采用模糊加权的中值滤波进行处理，相较于多种传统滤波方法，能更有效地去除椒盐噪声，保护图像细节。本文结合均值滤波和中值滤波，提出一种迭代自适应加权均值滤波（Iterative Adaptive Weighted Mean Filtering， IAWMF）算法，基于循环迭代思想，遍历图像的各个像素点，自适应调整滤波窗口尺寸，计算滤波窗口内非椒盐噪声像素灰度值的加权均值，替换中心点的噪声像素灰度值，在有效地滤除高密度椒盐噪声时，尽可能保持图像的细节信息。

1迭代自适应加权滤波算法原理

一幅含有噪声m×n的8位灰度图像U，uij为图像在（i，j）位置像素点的灰度值，0≤uij≤255，椒盐噪声像素的取值范围为0～255，0和255分别对应黑点与白点。

1.1噪声判断

为有效去除图像噪声，首先识别图像中的椒盐噪声，分别处理噪声和非噪声像素。判断椒盐噪声的方法较多，根据文献[11]和[14]的判断方法，如果像素在最小值0和最大值255之间，视为非噪声像素；如果像素灰度值为最小值0或最大值255，则视为椒盐像素。非噪声像素不处理，保持原像素值；椒盐像素由滤波算法处理。基于椒盐噪声的黑白点特性，不会漏判噪声像素，但存在噪声误判问题，对于高密度椒盐噪声污染图像，噪声误检对去噪效果的影响不大[14]。

针对含噪图像U，构建噪声标记矩阵F=[ fij]m×n，矩阵元素的取值fij为

fij=0，0＜uij＜2551，uij=0 oruij=255（1）

其中，fij=0时，uij为非噪声像素；fij=1时，uij为椒盐噪声。

1.2图像扩展

为了对图像外围的像素点进行滤波，将图像向四周扩展[15-16]，尺寸为m×n的原始图像U扩大为（m+2t）×（n+2t）的U-t，t∈1，2，…，minm，n，扩展方法如下：

1）以原始图像U的上边界为对称轴，将包含上边界的t×n部分的像素点向上反转，作为上边界扩展后的像素点；

2）以扩展后的图像下边界为对称轴，将包含下边界的t×n部分的像素点向下反转，作为下边界扩展后的像素点；

3）以扩展后的图像左边界为对称轴，将包含左边界的（m+2t）×t部分的像素点向左反转，作为左边界扩展后的像素点；

4）以扩展后的图像右边界为对称轴，将包含右边界的（m+2t）×t部分的像素点向右反转，作为右边界扩展后的像素点。

经过边界扩展后的图像U-t=u-rsm+2t×n+2t，u-rs表示在图像（r， s）位置上的像素

U-t=utt…ut1ut1ut2…utnutn…ut（n－t+1）u1t…u11u11u12…u1nu1n…u1（n－t+1）u1t…u11u11u12…u1nu1n…u1（n－t+1）u2t…u21610feee313f1165e58facaad1c5bd5d64de29ddfd98b50bab8f41dc0c600f0a1u21u22…u2nu2n…u2（n－t+1）u3t…u31u31u32…u3nu3n…u3（n－t+1）umt…um1um1um2…umnumn…um（n－t+1）umt…um1um1um2…umnumn…um（n－t+1）u（m－t+1）t…u（m－t+1）1u（m－t+1）1u（m－t+1）2…u（m－t+1）nu（m－t+1）n…u（m－t+1）（n－t+1）（m+2t）×（n+2t）（2）

原始图像U中的像素点uij对应扩展图像U-t中的像素点u-（i+t）（j+t），u-（i+t）（j+t）点对应的尺寸为2k+1的滤波窗口Ukij为

Ukij=u-（i+t－k）（j+t－k）…u-（i+t－k）（j+t+k）u-（i+t）（j+t）u-（i+t+k）（j+t－k）…u-（i+t+k）（j+t+k）（2k+1）×（2k+1）（3）

其中，k∈1，2，…，t。

1.3对噪声点进行滤波

对图像U检测出来的噪声点uij，以其为中心点，用滤波窗口的所有非噪声点的灰度值加权估计。根据窗口中的每个非噪声点urs与中心点uij的距离赋予相应的权值，距离近的像素与uij相关性强，相应权重大；距离远的像素与uij相关性弱，相应权重小。像素urs针对uij基于距离的加权系数w（urs，uij）为

w（urs，uij）=11+（r－i）2+（s－j）2（4）

设U︿kij为滤波窗口Ukij中非噪声点的像素的集合，噪声点uij的滤波输出u︿ij为

u︿ij=∑（r，s）∈U︿kijw（urs，uij）urs∑（r，s）∈U︿kijw（urs，uij）（5）

去噪所用的窗口大小直接影响去噪性能，小窗口的去噪有利于保留图形细节信息。但当噪声密度较高时，小窗口中可能不存在信号像素，无法估计噪声像素的灰度值，这时，必须增大窗口，以包含有用信号像素。对所有的噪声像素，先用3×3滤波窗口处理，如果不存在信号像素，则不处理；自适应增大滤波窗口尺寸，用5×5窗口处理，类似地，运用于7×7滤波窗口。设定最大的去噪滤波窗口尺寸为7×7，此时若还没有信号像素，则保持原来的噪声值。

经过一轮处理后，如果滤波去噪后输出的图像矩阵中还存在噪声点，则以此图像矩阵为基础进入下一轮滤波。

1.4算法步骤

步骤1： 构建含噪声图像矩阵U，设定最大迭代次数nummax，设num的初值为1、t的值为3；

步骤2： 如果迭代次数num大于nummax，则跳转至步骤10；否则，跳至步骤3；

步骤3： 构建U-t矩阵，遍历图像矩阵U，标记噪声点fij，如果fij=0，则跳至步骤3，继续遍历；如果fij=1，则跳至步骤4。遍历结束后，跳至步骤9；

步骤4： 令k=1，针对uij构建3×3滤波窗口矩阵Ukij，若存在非噪声像素，则跳至步骤8；否则，跳至步骤5；

步骤5： 令k=2，针对u&nbfiJmbyp3hEzR8uRsxtadeyGeS3F7lNoCqk4esvocJ2g=sp;ij构建5×5滤波窗口矩阵Ukij，若存在非噪声的像素，则跳至步骤8；否则，跳至步骤6；

步骤6： 令k=3，针对uij构建7×7滤波窗口矩阵Ukij，若存在非噪声的像素，则跳至步骤8；否则，跳至步骤7；

步骤7： 输出原像素值，跳至步骤3。如果到达最大滤波窗口仍没找到非噪声点，则暂不对其进行去噪处理，保持其原来的像素灰度值，将在下一轮循环中继续处理噪声点；

步骤8： 计算滤波窗口Ukij的非噪声像素的加权均值u︿ij，将uij用u︿ij替换，跳至步骤3；

步骤9： 遍历完所有的图像点uij后，num加1，并跳至步骤2。以滤波处理后的图像Y为基础，进行下一轮滤波；

步骤10： 输出最后的去噪图像Y。

后面仿真实验中，在椒盐噪声密度80%时，经过有限次迭代，滤掉绝大部分噪声。设置最大迭代次数nummax是为了防止噪声密度100%时，算法进入死循环。

算法流程如图1所示。

2仿真结果与分析

2.1去噪效果主观评价

为测试滤波性能，选取青岛卷烟厂电气控制柜内部线路的红外图像为研究对象，图像大小为512×512，灰度值8位。将均值滤波MF、标准中值滤波SMF、自适应中值滤波AMF、自适应模糊中值滤波AFMF及本文提出的迭代自适应加权均值滤波IAWMF 5种滤波算法在不同密度椒盐噪声的滤波效果进行比较，控制柜红外图像原图及加噪后的图像如图2所示。

各种滤波算法在低密度20%、高密度80%椒盐噪声下的去噪效果分别如图3和图4所示。均值滤波和标准中值滤波窗口尺寸为3×3，自适应滤波窗口最大尺寸为7×7，循环迭代次数为4。

由图3和图4可以看出，MF对噪声的适应能力很差，当噪声密度增加到80%时，滤波后的图像中存在明显的噪声残留，图像严重失真。SMF在高噪声密度下的去噪效果也较差，图像中的噪声残留较多。在高噪声密度下，AMF有一定的噪声残留，AFMF的滤波效果较好，而IAWMF的滤波效果最好，在滤波的同时有效地保护了图像细节。

2.2去噪效果客观评价

采用峰值信噪比PSNR和结构相似性指数SSIM 2种指标[17]评定各滤波算法的效果，即

PSNR（X，Y）=10×lg25521mn∑mi=1∑nj=1（xij－yij）2（6）

SSIM（X，Y）=2μXμY+c12σXY+c2μ2X+μ2Y+c1σ2X+σ2Y+c2（7）

其中，X为原图像；Y为处理后的图像；μX和μY分别表示X和Y的平均值；σX和σY分别表示X和Y的标准差；σXY为X和Y的协方差；c1=（k1L）2，c2=（k2L）2是确保分母不为零的常数；L=255为灰度值最大值，k1=0.01，k2=0.03为默认常数；PSNR和SSIM值越大，去噪效果越好。

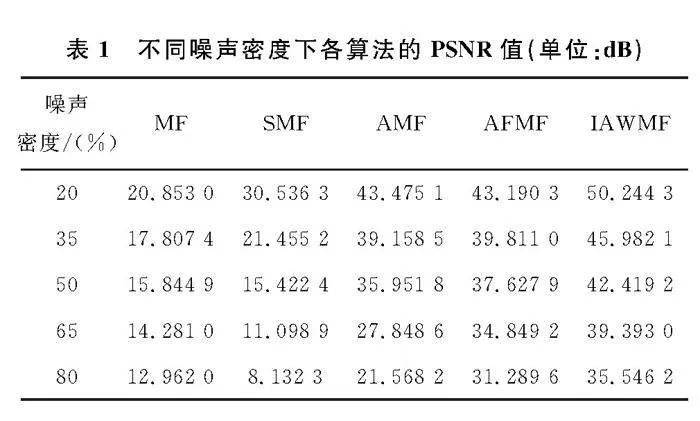
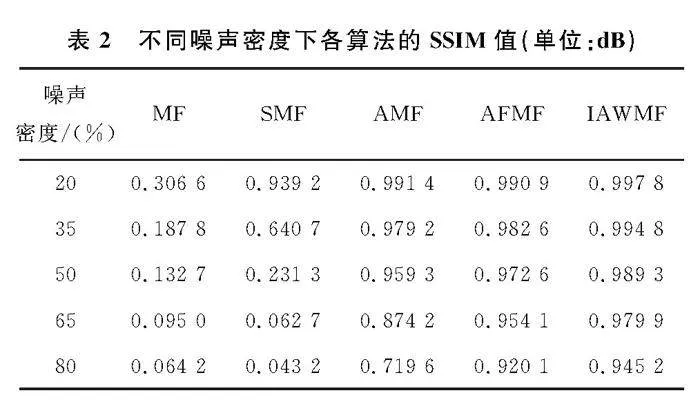
在椒盐噪声密度20%、35%、50%、65%和80%下，控制柜红外图像在不同噪声密度下5种滤波算法的PSNR值和SSIM值分别如表1和表2所示。

比较表1、表2中的数据，无论PSNR值还是SSIM值，MF和SMF算法的取值都偏低，在高密度噪声时更明显，去噪性能较差，这是由于2种算法都没有区分噪声像素和非噪声像素，损坏非噪声像素的缘故。比较表1中AMF、AFMF和IAWMF 3种滤波算法的PSNR值，在处理高密度噪声时AMF的取值最低，去噪效果差；处理低密度和高密度噪声时AFMF的取值较高，去噪效果较好；而IAWMF无论低密度还是高密度噪声取值都是最大的，PSNR值在噪声密度80％时为35.55 dB，高于AFMF算法4.26 dB，去噪效果最好。比较表2中AMF、AFMF和IAWMF 3种滤波算法的SSIM值，可得出同样的结论。

3结论

本文提出了一种迭代自适应加权均值滤波IAWMF算法。通过对图像边缘进行横向和纵向扩展，对图像边缘像素点进行滤波处理。IAWMF只对噪声点进行滤波，对非噪声点不做任何处理，避免传统滤波算法对非噪声点检测和替换带来细节信息丢失，对噪声点自适应调整滤波窗口尺寸，将窗口内非噪声像素值的加权平均作为中心像素滤波输出值，采用迭代循环处理结构，提升算法的去噪能力。与 MF、SMF、AMF、AFMF 4种滤波算法仿真分析比较，IAWMF不仅在低密度噪声优势明显，在高密度噪声时去噪效果也突出，控制柜红外图像细节清晰，滤波性能更优。

参考文献：

［1］岗萨雷斯. 数字图像处理[M]. 阮秋琦等， 译. 北京： 电子工业出版社， 2007.

［2］IBRAHIM H， KONG N S P. Simple adaptive median filter for the removal of impulse noise from highly corrupted image[J]， IEEE Transactions on Consumer Electronics， 2008， 54（4）： 1920-1927.

［3］SAGAR P， UPADHYAYA A， MISHRA S K， et al. A circular adaptive median filter for salt and pepper noise suppression from MRI images[J]. Journal of Scientific & Industrial Research， 2020， 79（10）： 941-944.

［4］韩涛， 孙科. 自适应中心加权的改进均值滤波算法[J]. 通信技术， 2019， 52（1）： 86-90.

［5］江巨浪， 章瀚， 朱柱， 等. 高密度椒盐噪声的多方向加权均值滤波[J]. 计算机工程与应用， 2016， 52（6）： 204-208.

［6］王松林， 蒋峥. 改进的自适应加权中值滤波算法[J]. 传感器与微系统， 2016， 35（11）： 128-131.

［7］陈健， 郑绍华. 基于方向中值的图像椒盐噪声检测算法[J]. 计算机应用， 2012， 32（10）： 2790-2792， 2797.

［8］马丽圆， 常锦才. 一种迭代的自适应中值滤波算法[J]. 计算机工程与软件， 2020， 41（9）： 69-71.

［9］兰霞， 刘欣鑫， 沈焕锋， 等. 一种消除高密度椒盐噪声的迭代中值滤波算法[J]. 武汉大学学报， 2017， 42（12）： 1731-1737.

［10］陈家益， 董梦艺， 战荫伟， 等. 中值检测的迭代中值滤波算法[J]. 现代电子技术， 2020， 43（7）： 70-77.

［11］王拓， 王洪雁， 裴炳南. 一种消除椒盐噪声的迭代自适应中值滤波算法[J]. 电光与控制， 2019， 26（2）： 23-27.

［12］TOH K K V， MAT ISA N A. Noise adaptive fuzzy switching median filter for salt and pepper noise reduction[J]. IEEE Signal Processing Letter， 2010， 17（3）： 281-284.

［13］万丰丰， 周国民， 周晓. 一种去除椒盐噪声的自适应模糊中值滤波算法[J]. 浙江大学学报（理学版）， 2019， 46（4）： 445-453.

［14］张成斌， 王开福. 基于形态开闭算子的高浓度椒盐噪声去除方法[J]. 计算机工程， 2015， 41（2）： 199-202.

［15］ENGINOGLU S， ERKAN U， MEMIS S. Pixel similaritybased adaptive riesz mean filter for saltandpepper noise removal[J]. Multimedia Tools and Applications， 2019（1）： 1-18.

［16］ERKAN U， ENGINOGLU S， THANH D N H， et al. adaptive frequency median filter for the salt and pepper denoising problem[J]. IET Image Processing， 2020， 14（7）： 1291-1302.

［17］陈家益， 战荫伟， 曹会英， 等. 邻域均值检测的迭代加权中值滤波算法[J]. 计算机应用研究， 2020， 37（6）： 1906-1915.

An Iterative Adaptive Weighted Mean Filter for Removing Salt and Pepper Noise

QIN Chenggang1， ZHANG Jian1， SHI Ganming1， ZHANG Xuege2， XIE Jingxin3， XU Shixu3

（1. China Tobacco Shandong Industrial Co.， Ltd. Qingdao Cigarette Factory， Qingdao 266101， China;

2. China Tobacco Shandong Industrial Co.， Ltd.， Jinan 250014， China;

3. School of Automation， Qingdao University， Qingdao 266071， China）

Abstract：

Aiming at the shortcomings of traditional mean filtering and multiple median filtering that cannot effectively remove highdensity salt and pepper noise， an iterative adaptive weighted mean filtering algorithm is proposed in this paper. In order to filter the peripheral pixels of the image， the image is first expanded along the surrounding areas. According to the extreme characteristics of salt and pepper noise， pixels are divided into noise points and signal points. For noisy pixels， multiple iterations are used to fully utilize the results of the previous filtering. The weighted average of the grayscale values of nonnoisy points in the filtering window is calculated， and the weighting coefficient is calculated based on the spatial distance from the center pixel of the window; the original values of nonnoise signal points is kept. The filtering window size adaptively increases from small to large based on whether there are nonnoise pixels in the window. In order to verify the effectiveness of the algorithm， five different algorithms are selected for simulation and comparison within the noise density range of 20% to 80%， and evaluation and analysis are conducted from both subjective and objective perspectives. The simulation results show that compared with the other four algorithms， this algorithm has significant advantages in peak signaltonoise ratio （PSNR） and structural similarity index （SSIM） under lowdensity noise， and still maintains prominent effects at 80% highdensity noise. The PSNR value is at least 4.26 dB higher than other methods. Visual observation also verifies that this algorithm has better filtering performance against highdensity salt and pepper noise， and well preserves the texture edges and details of the image.

Keywords：

salt and pepper noise; image extension; mean filtering; median filtering; iterative adaptive weighted mean filter

收稿日期： 2024-05-20； 修回日期： 2024-07-02

基金项目： 山东中烟工业有限责任公司科技基金资助项目（202201025）

第一作者： 秦承刚（1969-），男，本科，高级工程师，主要研究方向为应用电子技术。

通信作者： 徐世许（1965-），男，博士，教授，主要研究方向为工业自动化、图像处理。Email： xsxxsx65@163.com