电控减振器悬架NSGA-Ⅱ算法天地棚混合控制策略

文章编号： 1006-9798（2024）03-0078-08； DOI： 10.13306/j.1006-9798.2024.03.011

摘要： 针对具有电控减振器（Electronic Shock Absorber，ESA）的半主动悬架系统控制策略参数设定问题，即天地棚混合控制策略阻尼及分配系数设定，提出了基于非支配排序遗传（Nondominated Sorting Genetic AlgorithmsⅡ， NSGAⅡ）算法的天地棚混合控制策略。首先构建四分之一半主动悬架系统模型，搭建ESA正、逆模型，为解决天地棚混合控制策略中参数整定问题，通过NSGAⅡ算法进行优化，在MATLAB/Simulink环境下，分别开展典型随机路面与其叠加凸块路面工况下的仿真实验；针对适应度函数得到对应帕累托解集，对不同优化侧重点进行仿真实验，与无控制被动悬架进行对比分析，验证了本算法在一定程度上对汽车行驶平顺性改善。

关键词： 电控减振器； 半主动悬架； NSGAⅡ； 混合控制

中图分类号： U463.1文献标识码： A

悬架系统作为汽车底盘的重要组成部分之一，直接关系到车辆平顺性和操纵稳定性。传统被动悬架系统难以满足现阶段的性能需求，而主动悬架因耗能较高，成本昂贵等问题较难普及[1]。电控减振器（Electronic Shock Absorber，ESA）作为半主动悬架系统的部件之一，通过实时调节悬架阻尼适应不同驾驶条件，在各种路况下都能保持相对稳定。因此，有效设计并实现对电控减振器的控制具有十分重要的意义。国内外许多学者利用智能算法研究半主动悬架。基于萤火虫算法（Firefly Algorithm，FA）和粒子群算法（Particle Swarm Optimization，PSO）优化智能模糊逻辑的权重因子，结果表明FA算法在悬架动行程方面效果较优，PSO算法在车身垂向加速度方面效果更优[2]；采用遗传算法控制半主动悬架系统，改善了车辆的平顺性[3]；基于NSGAⅡ算法改进天棚及连续天棚的结果表明，连续天棚策略在乘坐舒适性方面更优，改进天棚策略在安全性方面表现良好[4]；基于NSGAⅡ算法优化模糊PID参数，并针对减速带工况及高频路面工况开展实验研究，验证了改进策略对乘坐舒适性有较好改善[5]；并联式惯容器弹簧阻尼（InerterSpringDamper，ISD）系统通过NSGAⅡ算法优化参数，对车辆行驶平顺性与操纵稳定性有一定改善[6]；运用改进遗传算法优化半挂牵引车悬架系统，车辆的平顺性及操纵稳定性得到有效改善[7]；应用NSGAⅡ优化响应面模型提升了车辆操纵稳定性[8]；NSGAⅡTLQR控制策略可改善车身加速度、悬架动行程及轮胎动载荷[9]；利用约束NSGAⅡ算法优化减振器结构参数，使车辆行驶平顺性得到提高[10]。目前，针对具有电控减振器的半主动悬架研究较少。基于此，本文以具有ESA的半主动悬架为主要研究对象，构建其正、逆模型，基于NSGAⅡ算法优化设计天地棚混合半主动悬架系统的控制策略，利用典型随机路面工况与其叠加凸块路面开展仿真实验。

1模型搭建

1.1四分之一悬架模型搭建

针对悬架系统动力特性研究，为简化问题，搭建二自由度的四分之一半主动悬架模型[11]如图1所示。整车系统模型参数为簧上质量ms=275 kg；簧下质量mt=40 kg；悬架刚度k=15 000 N/m；悬架固有阻尼cs=1 000 N·s/m；轮胎刚度kt=150 000 N/m。

根据牛顿第二定律，行驶动力学方程为

msz··s+cs（z·s－z·t）+k（zt－q）+F=0mtz··t－cs（z·s－z·t）－k（zs－zt）+kt（zt－q）=0（1）

其中，q为车轮路面激励输入，m；zs为簧上质量垂向位移，m；zt为簧下质量垂向位移，m；cs为悬架固有阻尼，N·s/m；z·s为簧上质量垂向速度，m/s；z·t为簧下质量垂向速度，m/s；z··s为簧上质量垂向加速度，m/s2；z··t为簧下质量垂向加速度，m/s2。选取状态变量x=zsz·sztz·tT，输出变量y=zs-ztz··szt-qT，输入量u=FqT。建立状态空间表达式为

x·=Ax+Buy=Cx+Du（2）

得到各变量与系数矩阵的具体形式为

A=0100－kms－csmskmscsms0001kmtcsmt－k+ktmt－csmtB=001ms000－1mtktmtC=10－10－kms－csmskmscsms1000D=001ms00－1（3）

通过电流驱动可改变ESA电磁阀开度，以实时改变阻尼系数，可变阻尼力F为

F=cf（z·s－z·t）（4）

其中，cf为ESA可调阻尼系数，N·s/m。

1.2路面模型搭建

以滤波白噪声路面激励及其叠加凸块路面激励分别作为路面输入[12]，即

q·1（t）=－2πn1uq1（t）+2πn0Gq（n0）uω（t）（5）

q2（t）=h01－cos2πuL（t－t0）t0≤t<t0+T0t<t0，t≥t0+T（6）

其中，q1、q2分别为滤波白噪声路面激励与凸块路面激励，m；n1为时间频率，Hz，n1=0.011 Hz；n0为标准空间频率，Hz，n0=0.1 Hz；Gq为路面不平度系数；ω（t）为单位高斯白噪声；u为车辆速度，m/s。L为凸块的宽度，m；h0为凸块截面垂直高度，m；t0为车轮开始接触凸块的时刻，s；T为车轮通过凸块的时间，s；t为时间，s。

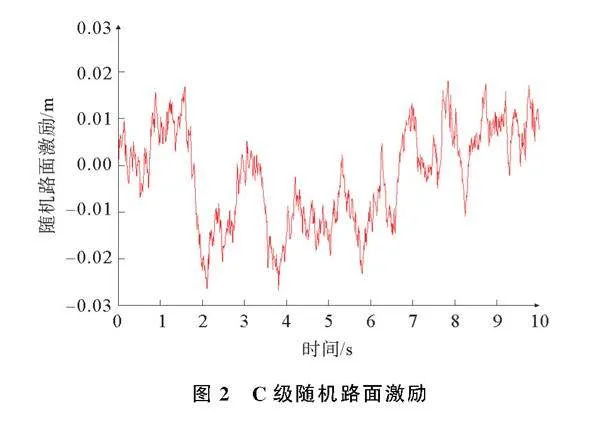
根据式（5）和式（6）所搭建的C级路面激励及凸块路面激励分别如图2和图3所示。

1.3ESA模型搭建

采用ESA作为半主动悬架的执行器，通过控制驱动电流改变阻尼系数，其输出阻尼力取决于减振器相对运动速度及驱动电流，ESA正、逆模型表示为

F=f（I，Δv）I=f（F，Δv）（7）

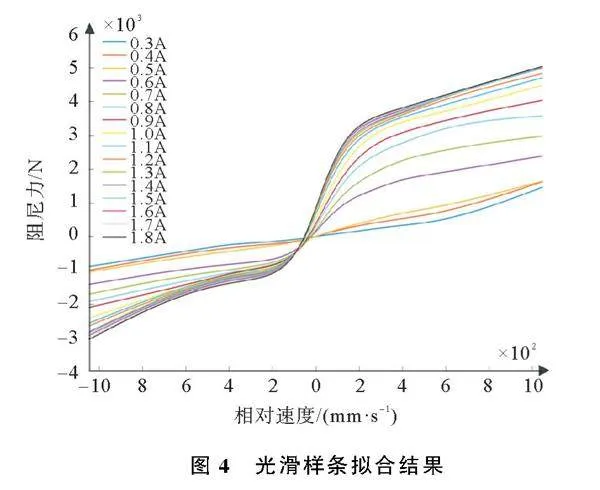
其中，F为减振器输出阻尼力，N；I为减振器驱动电流，A；Δv为悬架相对运动速度，m/s；根据减振器外特性实验数据，采用非参数查表插值模型[13]，ESA电磁阀存在失效保护模式，因此输入驱动电流范围为0.3～1.8 A，电流步长为0.1 A，拉伸压缩速度分别为0.052 m/s、0.131 m/s、0.262 m/s、0.524 m/s以及1.048 m/s[14]。通过光滑样条拟合减振器外特性实验数据，得到不同驱动电流下相对速度与阻尼力之间的关系，拟合原理表示为

RSS（f，λ）=∑Ni=1（yi－f（Ii，Δvi））2+λ∫（f″（Ii，Δvi））dt（8）

其中，yi为原始数据;λ为光滑拟合系数，λ越趋近于0，与原始数据重合度越高，反之趋近于∞拟合曲线越平滑。

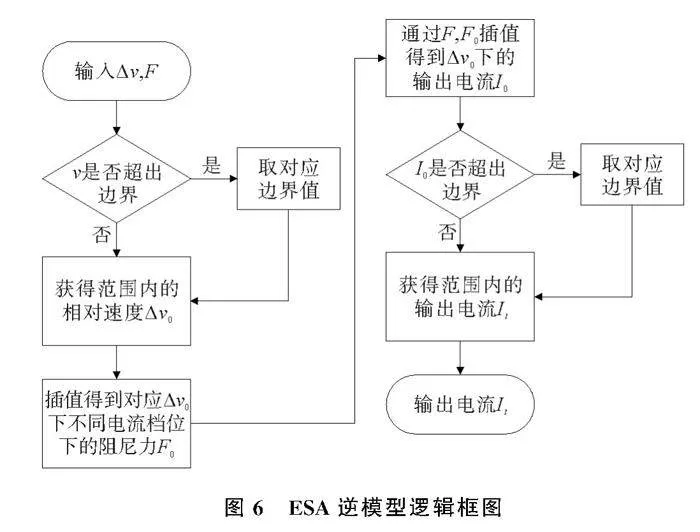
多次拟合后得到符合要求的拟合函数及曲线如图4所示，通过线性回归平滑处理，得到“电流阻尼力相对速度”MAP图如图5所示，通过MATLAB/Simulink中的Prelookup模块与Lookup Table模块插值查表，搭建ESA正、逆模型。正模型由逆模型输出电流及悬架相对运动速度插值得出对应阻尼力，建模流程相对简单。逆模型建模流程如图6所示，为避免策略输出电流过大损坏减振器，对输出电流设置边界值。

由图4与图5可知，根据示工数据所建立ESA逆模型较为准确。ESA逆模型逻辑框图由图6所示。

2控制策略构建

2.1NSGAⅡ算法

NSGAⅡ算法是一种基于帕累托最优概念的遗传算法[15]，通过对种群进行快速非支配排序、选择、交叉和变异，利用拥挤度计算和精英保留策略选择合适的个体，提高算法效率，能够在全局区域中快速获得多目标的优化搜索，避免陷入局部收敛。

NSGAⅡ算法是寻找帕累托最优解集，采用快速非支配性排序方式，依据个体的解对种群产生的优劣影响进行分层，种群中不受任何其他个体的解所支配的解集构成帕累托前沿，同一层次非支配解的多样性可使解均匀地分布在帕累托前沿。为达成此目标，采用计算拥挤距离的方式，除边界值被赋予无穷距离值之外，其余解被赋予与之相邻的两个解的函数值归一化后差值绝对值相同的距离值，总的拥挤距离为每个目标值的各个距离之和，即

L［i］dis=L［i］dis+L［i+1］n－L［i－1］nfmaxn－fminn（9）

其中，L[i]dis为第i个个体解的拥挤距离；L[i+1]n为第i+1个个体第n个目标函数值；fmax&nbsp;n、fminn分别为集合中第n个目标函数的最大值与最小值。

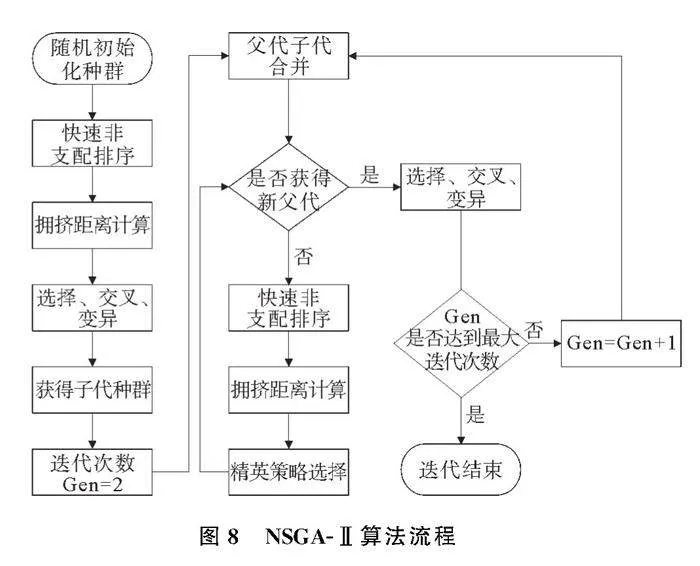
为避免在寻优过程中最优解被丢失，算法采用精英保留策略，执行过程如图7所示。假设初始个体数为N，通过交叉变异的到父代种群Gt和子代种群Ht，形成大小为2N的种群Rt。通过计算快速非支配排序及拥挤距离得到多个非支配集，按照非支配顺序对新的父本种群进行填充，若某一非支配集无法全部填充到新父本种群，则对其按照拥挤距离从大到小进行填充，直至得到新的父本种群Gt+1。NSGAⅡ算法流程如图8，基于此算法设计半主动悬架的天地棚混合控制策略。

2.2基于NSGAⅡ天地棚混合控制策略

天棚、地棚控制策略常应用于半主动悬架的控制，综合考虑行驶平顺性与操作稳定性，采用天地棚混合控制策略[16]为

FSG=λcskyz·s－（1－λ）cgroundz·tz·s（z·s－z·t）≥0&z·t（z·s－z·t）≤0－（1－λ）cgroundz·tz·s（z·s－z·t）<0&z·t（z·s－z·t）≤0λcskyz·sz·s（z·s－z·t）≥0&z·t（z·s－z·t）>00z·s（z·s－z·t）<0&z·t（z·s－z·t）>0（10）

其中，FSG为控制策略输出阻尼力，N；λ为天地棚比例调节参数，范围0～1；csky、cground分别为天棚阻尼系数和地棚阻尼系数，N·s/m。悬架的控制效果取决于天地棚阻尼系数及天地棚比例调节参数，针对不同的路面激励，悬架的振动特性也有所差别，故上述3个参数的选择决定控制策略的优劣。通过NSGAⅡ算法对3个参数进行遴选，设置适应度函数[17]为

minf=［f1，f2，f3］Τ；f1=RMS（z··s）RMS（z··sp）；f2=RMS（zs－zt）RMS（zsp－ztp）；f3=RMS（zt－q）RMS（ztp－q）（11）

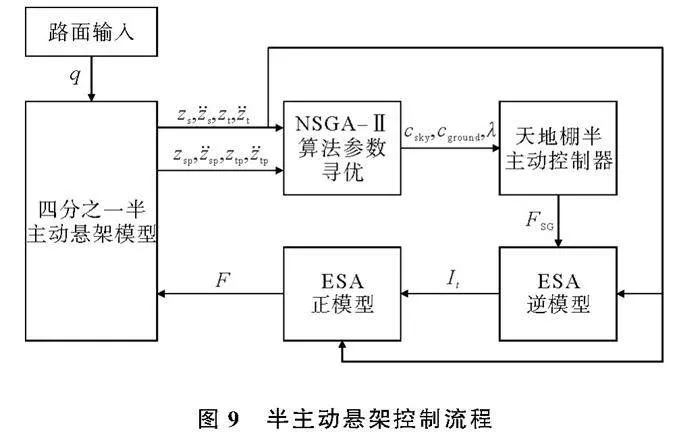
其中，RMS（·）为均方根值；z··sp为无控制被动悬架簧上质量垂向加速度，m/s2；zsp为无控制被动悬架簧上质量垂向位移，m；ztp为无控制被动悬架簧下质量垂向位移，m；q为路面激励，m。考虑实际ESA阻尼调节处于一定范围，在保证安全的前提下，兼顾车辆行驶平顺性，在迭代过程中对于天地棚阻尼系数设置取值范围。具体控制流程如图9所示，从半主动悬架模型中获取天地棚混合策略所需信号，利用NSGAⅡ算法遴选，获得满足控制需求的策略参数，通过天地棚半主动控制器将期望输出的阻尼力传递到ESA逆模型，由逆模型插值查表得到目标电流并输出到正模型，得到ESA产生的真实阻尼力。

3仿真结果

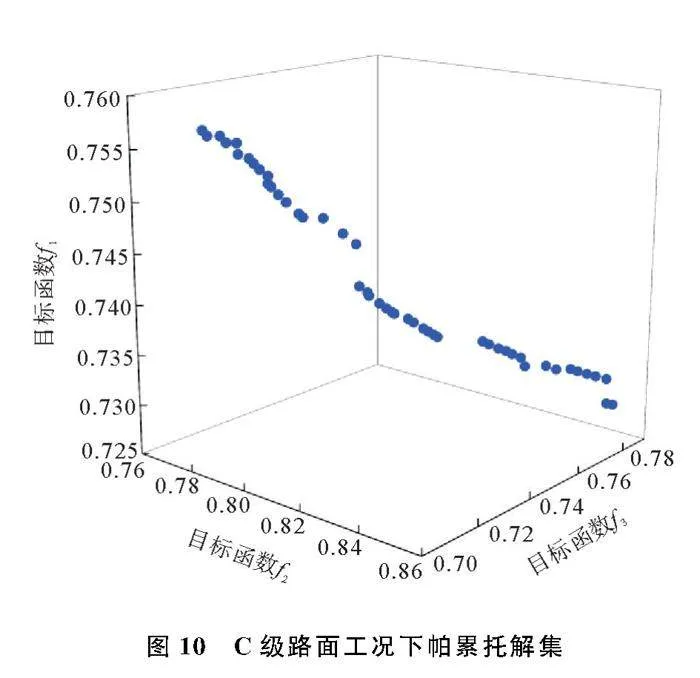
为研究基于NSGAⅡ优化的天地棚混合控制策略对具有ESA的半主动悬架系统的控制效果，将C级随机路面激励与其叠加凸块路面激励分别作为激励输入进行仿真验证。仿真车速均为40 km/h，设置NSGAⅡ算法参数，种群数量为50，交叉概率为0.7，变异概率为0.4，经过200次迭代得到上述2种工况下的帕累托最优解集。

3.1C级随机路面工况

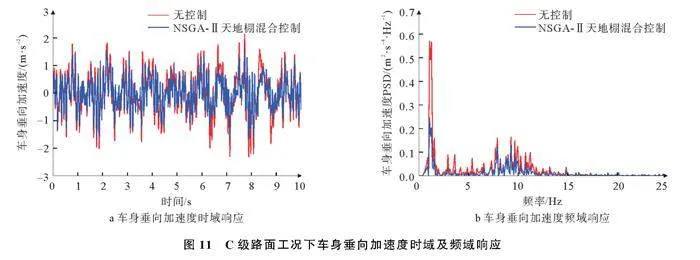
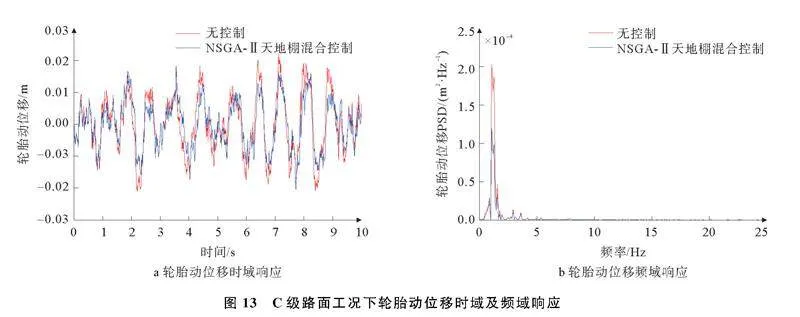
C级路面工况帕累托解集如图10，车身垂向加速度、悬架动行程、轮胎动位移时域及频域响应分别如图11～图13所示。

由图11～图13可以看出，与无控制相比，NSGAⅡ天地棚混合控制下车身垂向加速度在1.5 Hz附近与7～12 Hz之间幅值有一定程度减小，悬架动行程与轮胎动位移在1.5 Hz附近幅值均有不同程度减小，验证所设计控制策略在频域内有一定效果。

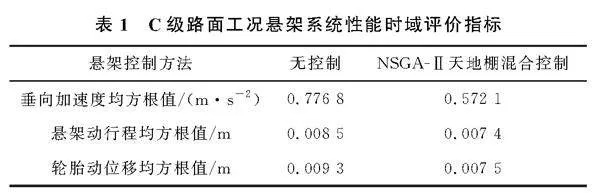
为能更加直观显示使所设计控制策略效果，采用簧上质量垂向加速度、悬架动行程、轮胎动位移作为评价指标，分别计算C级路面工况无控制与NSGAⅡ天地棚混合控制下的3个指标均方根值如表1所示。

根据表1，与无控制被动悬架相比，在C级路面工况下，引入NSGAⅡ天地棚混合算法后，车身垂向加速度均方根值降低26.35%，悬架动行程均方根值降低12.94%，轮胎动位移均方根值降低19.35%，行驶平顺性得到改善。

3.2叠加路面激励工况

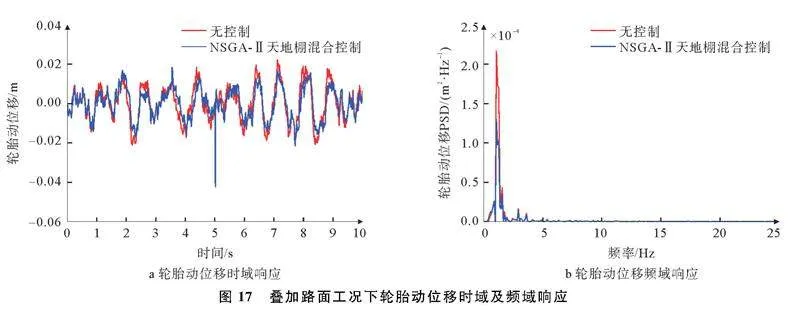
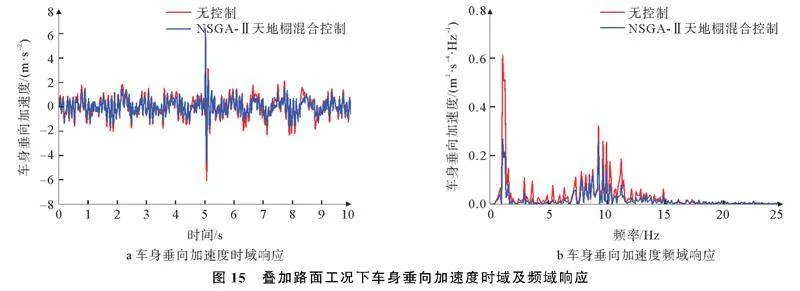
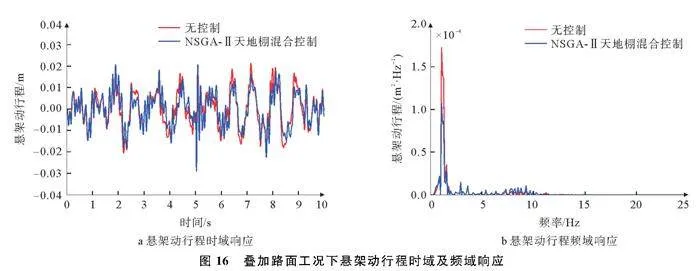
叠加路面工况帕累托解集如图14所示，车身垂向加速度、悬架动行程、轮胎动位移时域及频域响应图如图15～图17。

由图15～图17可知，与无控制相比，NSGAⅡ天地棚混合控制下车身垂向加速度在1.5 Hz附近与5～15 Hz之间幅值有一定程度减小，悬架动行程在1.5 Hz附近与7～10 Hz之间幅值均有不同程度减小，轮胎动位移在1.5～3 Hz之间幅值有一定程度减小，验证所设计控制策略在频域内有一定效果，证明应用算法的控制策略改善了悬架性能。

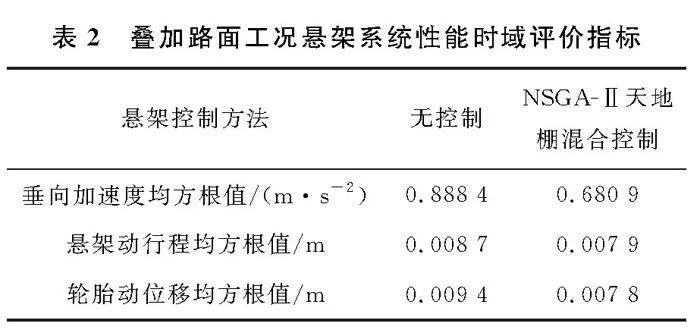
为能更加直观显示使所设计控制策略效果，采用簧上质量垂向加速度、悬架动行程、轮胎动位移作为评价指标，分别计算叠加路面工况无控制与NSGAⅡ天地棚混合控制下的3个指标均方根值，如表2所示。根据表2可得，与无控制被动悬架相比较，在叠加路面工况下，引入NSGAⅡ天地棚混合算法控制后车身垂向加速度均方根值降低23.35%，悬架动行程方根值降低9.19%，轮胎动位移均方根值降低17.02%，行驶平顺性得到改善。

4结论

通过利用MATLAB/Simulink建立了二自由度四分之一半主动悬架模型，搭建ESA正、逆模型和典型随机路面模型与叠加凸块路面模型，以半主动悬架的车身垂向加速度、悬架动行程、轮胎动位移作为性能指标，设计适应度函数，提出基于NSGAⅡ天地棚混合控制的半主动悬架控制策略。对NSGAⅡ算法中的种群数量、交叉概率、变异概率等参数进行选取，基于适应度函数对所提出控制策略参数进行遴选，优化天地棚混合控制策略的参数选取，在C级随机路面及叠加凸块路面进行迭代与仿真实验，得到对应工况下的帕累托解集，验证了NSGAⅡ天地棚混合控制策略改善车辆行驶平顺性。

参考文献：

［1］林长波， 王越， 许恩永， 等. 半主动悬架改进ADD控制策略研究[J]. 噪声与振动控制， 2023， 43（1）： 197-202.

［2］TALIB A H M， DARUS M Z I. Intelligent fuzzy logic with firefly algorithm and particle swarm optimization for semiactive suspension system using magnetorheological damper[J]. Journal of Vibration and Control， 2017， 23（3）： 501-514.

［3］SIMONE T， SERGIO M， et al. Batch reinforcement learning for semiactive suspension control[C]∥IEEE Control Applications. Russia： IEEE， 2009， 528-587.

［4］KHADR A， HOUIDI A， ROMDHANE L. Design and optimization of a semiactive suspension system for a twowheeled vehicle using a full multibody model[J].Proceedings of the Institution of Mechanical Engineers， Part K： Journal of Multibody Dynamics， 2017， 231（4）： 630-646.

［5］董轲建. 车辆半主动悬架控制策略及优化研究[D]. 重庆： 重庆交通大学， 2023.

［6］王丹. 车辆垂向振动系统惯容器悬挂参数研究[D]. 常州： 常州大学， 2023.

［7］赵向阳， 吴启斌. 基于改进遗传算法的半挂牵引车平顺性与操稳性协同优化[J]. 兰州理工大学学报， 2022， 48（2）： 61-66.

［8］苏伟伟， 晋民杰， 范英. 基于响应面法的悬架优化与操纵稳定性分析[J]. 大连交通大学学报， 2022， 43（4）： 55-59.

［9］杨程. 考虑响应时滞的磁流变半主动悬架最优控制研究[D]. 南昌： 华东交通大学， 2023.

［10］顾信忠， 李浩. 空气弹簧悬架系统减振器的优化设计[J]. 常熟理工学院学报， 2023， 37（5）： 93-100.

［11］李勇凯. 轮毂电机驱动电动汽车平顺性分析与控制研究[D]. 锦州： 辽宁工业大学， 2019.

［12］龙江启， 向锦涛， 俞平， 等. 适用于非线性主动悬架滑模控制的线性干扰观测器[J]. 吉林大学学报（工学版）， 2021， 51（4）： 1230-1240.

［13］张丽霞， 李宁斐， 梁冠群， 等.阻尼连续可调半主动悬架平滑天棚控制策略研究[J]. 噪声与振动控制， 2023， 43（2）： 169-173， 184.

［14］中国国家标准化管理委员会汽车简式减振器台架实验方法[S]. 中国标准化出版社， 1999.

［15］DEB K， AGRAWAL S， PRATAP A， et al. A fast and elitist multiobjective genetic algorithm： NSGAⅡ[J]. IEEE Transactions on Evolutionary Computation， 2002， 6（2）： 182-197.

［16］湛永全. MSAC路面不平度等级识别下的馈能悬架SHGH切换控制[D]. 秦皇岛： 燕山大学， 2023.

［17］张进秋， 黄大山， 姚军. 车辆悬架系统振动控制[M]. 北京： 国防工业出版社， 2020.

NSGAⅡ Algorithm Hybrid Control Strategy for Electronic Control Shock Absorber Suspension in Skyroof

HE Pu1， WEI Wenzhi2， SUN Jingzhe2， YAN Tianyi2

（1. XGM Co. Ltd.Shanghai B ranch， Shanghai 201799， China;

2. College of Mechanical and Electrical Engineering， Qingdao University， Qingdao 266071， China）

Abstract：

A hybrid skyhookgroundhook control strategy based on the Nondominated Sorting Genetic Algorithm Ⅱ （NSGAⅡ） is proposed to address the parameter setting issues in semiactive suspension systems with Electronic Shock Absorbers （ESA）. This includes setting the damping and distribution coefficients. A quartercar semiactive suspension system model is constructed， and ESA forward and inverse models are developed. The NSGAⅡ algorithm optimizes the parameter tuning problem in the hybrid skyhookgroundhook control strategy. Simulations are conducted in MATLAB/Simulink under typical random road conditions and random road with bump conditions. The Pareto front is obtained for the fitness function. Simulations are carried out with different optimization focuses. Comparative analysis with passive suspension without control demonstrates that the proposed algorithm improves ride comfort to some extent.

Keywords：

electronic shock absorber; semiactive suspension; NSGAⅡ; hybrid control

收稿日期： 2024-05-28； 修回日期： 2024-07-21

基金项目： 山东省自然科学基金面上资助项目（ZR2016EEM49）； 国家自然科学基金资助项目（51475248）

第一作者： 何浦（1976-），男，硕士，工程师，主要研究方向为负责电控减振器及主动悬架系统的开发与制造。

通信作者： 严天一（1970-），男，博士，教授，主要研究方向为车辆系统动力学及控制技术。Email： yan_7012@126.com