基于改进A*算法的AGV路径规划研究

文章编号： 1006-9798（2024）03-0013-07； DOI： 10.13306/j.1006-9798.2024.03.003

摘要： 针对传统A*算法在自动引导车（Automated Guided Vehicle，AGV）寻路时存在搜索路径规划时间长、搜索效率低和不考虑AGV运行体积等问题，提出以动态加权方式改进启发式估计函数中启发因子，根据路径实际情况选择加权值，筛选搜索邻域时节点，剔除必然使路径代价值升高的方向，以增加障碍物影响半径的方式，避免AGV导航过程中发生碰撞。仿真结果表明，相比于原始A*算法，改进后的A*算法路径节点搜索数量减少82%，时间减少81%，提高了路径规划效率，且考虑AGV运行的安全半径，保证了AGV运行的安全性，避免在实际导航时发生碰撞。

关键词： A*算法； 启发因子； 自动引导车； 路径规划

中图分类号： TP242.2文献标识码： A

路径规划是AGV的核心技术之一，在特定环境中寻找最优路径或多条路径，确保AGV稳定高效地运输货物[1-2]。目前AGV路径规划算法主要包括动态窗口法（Dynamic Window Approach， DWA）、迪杰斯特拉算法（Dijkstra）及A* 算法等[3]。A*算法因其高效性而被广泛应用，但也存在拐点冗杂、搜索效率低[4-6]等问题。对此，诸多学者进行优化改进。蔡梓丰等[7]通过实时阈值法和惩罚因子法，减少了不必要的搜索空间和冗余路径，显著提高了搜索和路径规划速度。加权曼哈顿距离引入转弯修正参数作为启发函数可优化管理遍历节点数，显著降低转弯频率，提升路径寻找效率和路径流畅性[8]。采用三领域与八领域混合搜索策略，有效缩短搜索时间、减少路径拐点数量[9]。吴晓岚等[10]提出了一种基于安全距离的Floyd删除算法，去除冗余路径点以减少路径长度。然而，上述研究大多集中在改善A*算法的搜索效率和路径质量，而对在动态环境下保证AGV运行体积安全性的考虑相对较少。为解决传统A*算法搜索路径计算量大和不考虑AGV运行体积的问题，本文提出一种改进A*算法，通过优化A*算法中启发式估计函数，采用动态加权方式改进其启发因子，根据路径实际情况设置加权值。同时，改进邻域关键节点的搜索方式，依据AGV起点和目标点的位置，对搜索方向进行筛选，为保证AGV路径规划的安全性，根据障碍物大小、AGV尺寸，设置障碍物安全半径。仿真实验验证了改进A*算法的路径规划效率及AGV运行的安全可靠性。

1传统A*算法

A*算法是一种启发式搜索算法[11]，是路径规划中的代表性算法，核心在于使用了启发式估计函数。启发式估计函数又称启发函数，通过估计起始节点经过节点n到达目标节点的代价值指导节点搜索方向。启发式估计函数公式为

f（n）=g（n）+h（n）（1）

其中，f（n）为实际代价值与代价估计值的总和；g（n）为起始节点到节点n到的实际代价值；h（n）是启发因子，用估计节点n到目标节点的代价估计值。

常见启发因子计算方式有切比雪夫距离、曼哈顿距离和欧几里得距离3种[12]。

1）切比雪夫距离表示当前和目标两节点之间坐标距离之差的最大值，即

h（n）=max（xn－x0，yn－y0）（2）

2）曼哈顿距离表示当前节点与目标节点在横轴和纵轴上的距离之和，即

h（n）=xn－x0+yn－y0（3）

3）欧几里得距离表示当前节点与目标节点的直线距离，即

h（n）=（xn－x0）2+（yn－y0）2（4）

A*算法节点选择示意图如图1所示，A*算法原理[13]是创建OPEN_LIST和CLOSE_LIST 2张表：将起始节点添加至CLOSE_LIST表中，将起始节点周围8个节点添加至OPEN_LIST表，计算每个节点的代价值f，将代价值最小的节点，即图中黄色节点，从OPEN_LIST表中移动到CLOSE_LIST表，并将代价值最小的节点作为新的起始节点，直到到达目标节点为止。

2基于改进A*算法的路径规划

传统A*算法原理简单，能够准确搜索到地图中最优路径，比较依赖启发函数，合适的启发函数有利于提高路径规划的性能，但传统A*算法未考虑空间约束，AGV导航风险系数增加，从而导致AGV受损。因此本文基于传统A*算法存在的问题进行改进。

2.1改进A*算法的启发函数

启发函数中预估代价值和实际代价值的大小会影响A*算法的路径搜索的效率和精度。当预估代价值小于实际代价值时，A*算法的节点搜索范围更广，搜索节点数量更多，能够保证生成最优路径，但搜索时间较长。反之，则搜索范围变小，搜索节点数量减少，路径规划时间短，但不能保证最优路径的生成[14]。为了权衡两者之间的关系，更加合理地实现路径规划算法，引入优化后的启发因子h（n），提出一种优化的启发因子距离公式。

本文优化距离以动态加权方式获取启发因子，根据路径实际情况选择加权值

h（n）=ω1×（xn－x0+yn－y0），xn－x0+yn－y0>λ，ω1≥1ω2×（xn－x0+yn－y0），xn－x0+yn－y0≤λ，0<ω2<1（5）

其中，x0和y0表示当前节点坐标；xn和yn表示目标节点坐标；λ表示阈值常数；ω1和ω2为权重。

规划路径时，既要考虑搜索速度又要考虑最优路径，此时需要使用式（5）动态加权的启发因子。以原本的启发因子h（n）为判断依据，当其高于阈值λ时，权重增大，算法搜索速度更快；当低于阈值λ时，权值降低，优先考虑最优路径。阈值根据计算机运算性能、地图尺寸等因素动态选择，权重值也根据设定地图的大小、复杂程度进行调节。

设置优化距离参数λ=18，ω1=3，ω2=0.8，在同一地图中，4种启发因子对比结果如图2所示，其中黑色线条为障碍物或边界，绿色圆点为开始位置，蓝色“x”符号为搜索节点，红色线条为路径规划结果，即最优路径。

由图2可以看出，使用4种启发因子规划的路径都能避过障碍物到达指定节点，与其他距离计算方法相比，本文优化距离搜索节点明显减少。与切比雪夫距离和欧几里得距离相比，本文优化距离的搜索路径转角更少，更符合实际情况。各启发因子路径搜索详细信息见表1。

由表1可以看出，使用本文优化距离的启发因子，搜索节点仅336个，路径规划时间为281.1 ms。仿真结果表明，本文采用的启发因子在保证路径准确的前提下，减少了路径搜索的时间消耗，显著提高了路径规划的效率。

2.2筛选搜索邻域关键节点

处于当前节点的AGV在地图上运动时，搜索相邻的8个节点，然后取其一作为目标节点进行运动[15]，当前节点运动图如图3所示。虽然从当前位置有8个方向可选择，但在有些地图中，部分方向不可能成为最优路径的一部分。起始位置及目标位置示意图如图4，图中绿色圆圈为起始位置，蓝色叉号为目标位置，处于当前节点的AGV，不需要搜索图3中相邻节点1、4、6，因为这3个节点一定会使代价值增大，因此可以对搜索邻域进行优化。

本文根据当前节点和终点的位置信息，采用参数化的方式选择可搜索方向，分类结果见表2。iCQB7ikPCT9yJ9Ow8lgtSlFu1hU/P7avagC/5W0v8/M=表中α为当前点与目标点的连线夹角，当前节点到相邻节点2的移动方向为0°。这种方法会舍弃8个方向中的3个方向，因为这3个方向的选点会使路径代价值升高，舍弃后可降低计算量，提高路径搜索的效率。

利用本文优化距离的启发因子，邻域搜索方法优化前后对路径搜索的节点如图5所示。相比于优化前，优化后的方法节点搜索数量明显减少，搜索节点数量为265，减少了21.1%，时间为192.1 ms，减少了31.7%。因此，优化后的邻域搜索算法提前避开代价值高的方向，减少节点搜索数量，提高路径搜索效率。

2.3设置障碍物影响半径

A*算法是以AGV中心坐标为基准进行路径规划，但在实际运行中需要考虑AGV的轮廓尺寸，本文

以AGV半径来增加障碍物影响半径，设定障碍物可影响范围公式为

R′o≥Ro+RAGV+d0（6）

其中，R′o为障碍物可影响半径；Ro为障碍物中心到边缘的半径；RAGV为AGV最大半径；d0为安全半径常数。

障碍物影响半径示意图如图6所示，虚线为搜索路径，Ro为障碍物实际半径，R′o为障碍物最小影响半径，RAGV为AGV最大半径，A、B、C表示AGV行驶路径上的节点。

A*算法以AGV中心为起始坐标进行路径规划，为了防止AGV和障碍物之间发生碰撞，基于相对距离原理，设置AGV运行半径，其实就是增加障碍物影响半径，因此将AGV最大半径加到障碍物实际半径上，保障AGV运行的安全，避免发生碰撞。

3路径规划实验

3.1仿真实验

3.1.1实验设计

为了验证改进A*算法在AGV全局路径规划中的有效性，使用A*算法、文献[8]算法、启发函数算法和改进算法分别在尺寸为20×20和50×50的栅格地图上进行仿真实验。在地图中按照复杂环境特征要求，设置了不同大小、形状及密集程度的障碍物，假设AGV运行的安全距离为1个栅格。

3.1.2实验结果与分析

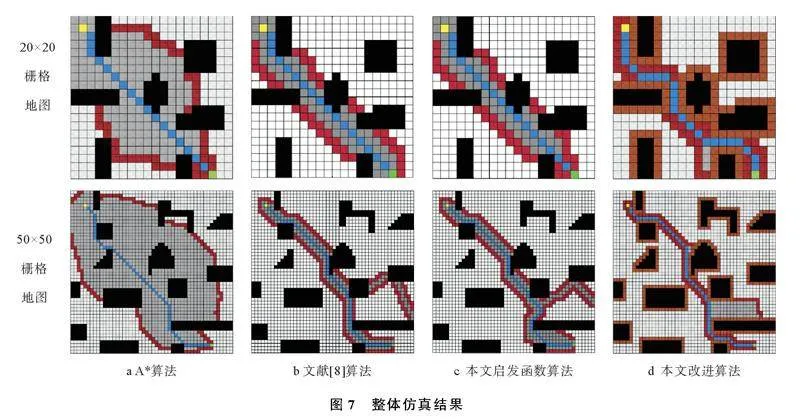
仿真图中黑色栅格为障碍物，白色栅格为可通行区域，黄色栅格为起始节点，绿色栅格为目标节点，灰色栅格为搜索完的CLOSE_LIST列表，红色栅格为待搜索的OPEN_LIST列表，棕色栅格为增加的障碍物影响半径。整体仿真结果如图7所示。

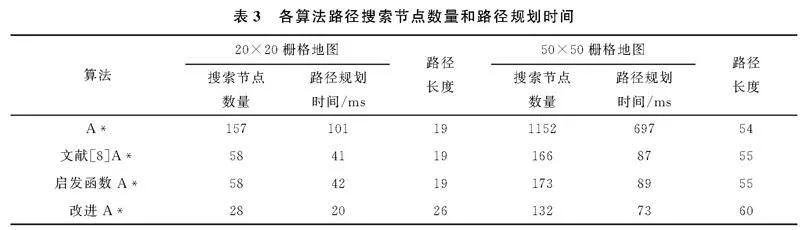
A*算法、文献[8]算法、启发函数算法和改进算法路径搜索节点数量、路径规划时间及路径长度见表3。

仿真结果表明，在20×20的栅格地图中，使用改进A*算法进行路径规划时，搜索节点仅为28个，路径规划时间为20 ms，相比于A*算法，搜索节点减少129个，时间减少81 ms，相比于文献[8]算法，搜索节点减少30个，时间减少21 ms。在50×50的栅格地图中，改进A*算法路径规划搜索节点仅为132个，路径规划时间为73 ms，相比于A*算法，搜索节点减少1 020个，时间减少606 ms，相比于文献[8]算法，搜索节点减少32个，时间减少14 ms。但改进A*算法规划路径长度增加，主要因为改进后增加了障碍物半径，导致AGV路程增加。综上所述，A*算法和改进A*算法均能在不同尺寸栅格地图下实现路径规划，改进A*算法搜索节点和时间明显减少，提高了路径规划效率，且考虑AGV运行的安全距离，避免在实际导航时发生碰撞。

3.2真实环境AGV导航实验

3.2.1实验设计

环境地图图像尺寸为440×550，采用46×58的栅格分割图像，每一格图像大小为9.6×4950828d64d2218b5d0d99bfb79d06849.5，实际运行环境大小为4.6 m×5.8 m，分割后每一个栅格表示真实环境大小为0.1 m×0.1 m。AGV在真实环境和栅格地图中位置如图8所示。

车间的工位发出调度AGV的需求，工位通过局域网和TCP传输协议将坐标位置信息传给上位机，上位机获取目标点在栅格地图中的位置（xb，yb），获取AGV在栅格地图中的坐标（36，52），再将其作为路径规划产生的第一个节点，目标点（xb，yb）为路径规划产生的最后一个节点。

3.2.2实验结果与分析

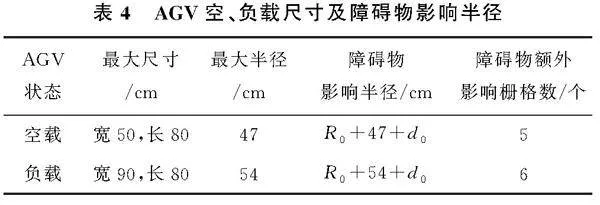
车间物流AGV在负载情况下，AGV尺寸会相应变换，分别针对AGV在空载和负载情况设置障碍物影响半径，并使用改进A*算法规划路径。AGV空、负载尺寸及障碍物影响半径见表4，其中，原障碍物影响半径为R0，设置安全半径常数d0=5 cm。

改进A*算法对空载AGV和负载AGV路径规划结果如图9所示。

路径规划仿真实验结果见表5，表中记录了使用改进A*算法，AGV在空载和负载情况下，路径规划搜索节点、规划时间、最优路径长度和AGV是否发生碰撞。

实验结果表明，基于改进A*算法的路径规划，空载和负载AGV均能实现路径的最优解，虽然不同状态下AGV路径导航的地图和起始点相同，但由于AGV负载时会导致AGV运行半径增加，增加的半径映射到障碍物上会加大障碍物影响半径，从而减少可运行区域，所以节点搜索数量、路径规划时间和最优路径长度都不同。综上，AGV在空载和负载情况下，改进A*算法均能规划出最优路径，且避免AGV与障碍物发生碰撞，实验结果符合路径规划的要求。

4结束语

本文针对AGV在真实地图下的导航，提出一种改进的A*算法，优化A*算法中启发式估计函数，采用动态加权方式改进启发因子，根据路径实际情况设置加权值。同时，改进邻域关键节点的搜索方式，依据AGV起点和目标点的位置，对搜索方向进行筛选，为保证AGV路径规划的安全性，根据障碍物大小、AGV尺寸，设置障碍物安全半径。经实验验证，相比于原始A*算法，改进A*算法节点搜索数量和时间明显减少，且保证了AGV运行的安全性，有效解决了传统A*算法搜索节点多、路径规划时间长和不考虑AGV运行体积的问题。但改进算法中的加权值需要根据地图大小和复杂程度动态调整，实际应用中可能存在一定困难，未来将进一步探索如何自适应确定加权值，提升算法的实用性和灵活性。

参考文献：

［1］WANG Z， HU X， Li X， et al．Overview of global path planning algorithms for Mobile Robots[J]．Computer Science， 2021， 48（10）： 19-29．

［2］李晓旭， 马兴录， 王先鹏． 移动机器人路径规划算法综述[J]． 计算机测量与控制， 2022， 30（7）： 9-19．

［3］ZHAO X， YE H， JIA W， et al． Survey on AGV path planning and obstacle avoidance algorithms[J]． Journal of Chinese Computer Systems， 2024， 45（3）： 529-541．

［4］陈骏， 沈琦琦． 自动导引车路径规划算法的研究综述[J]． 自动化与仪器仪表， 2023（9）： 8-15．

［5］陈晓冬， 王福威． 基于改进A～*算法的AGV路径规划[J]． 计算机系统应用， 2023， 32（3）： 180-185．

［6］张涌， 成海飞， 赵奉奎． 基于自适应A～*算法的自动驾驶车辆路径规划方法研究[J]． 重庆交通大学学报（自然科学版）， 2024， 43（2）： 115-121， 130．

［7］蔡梓丰， 张延生， 梁先樟， 等． 基于改进A～*算法的路径规划研究[J]． 现代信息科技， 2024， 8（10）： 51-55， 59．

［8］刘亚宁， 张东升． 基于改进A～*算法的AGV路径规划研究[J]． 信息与电脑（理论版）， 2023， 35（23）： 62-65．

［9］余震， 王栋， 王明天， 等． 基于改进A～*算法的AGV全局路径规划[J]． 武汉科技大学学报， 2024， 47（3）： 234-240．

［10］WU X L， ZHANG Q Y， BAI Z F， et al． A selfadaptive safe A* algorithm for AGV in largescale storage environment[J]． Intelligent Service Robotics， 2024， 17（2）： 221-235．

［11］王向宇． 基于改进A～*算法和动态窗口法的室内移动机器人路径规划研究[D]． 赣州： 江西理工大学， 2023．

［12］杨聿壬， 郭江宇， 董晓峰， 等． 基于改进A～*算法的安全路径规划[J]． 电脑知识与技术， 2024， 20（9）： 1-4， 11．

［13］宣仁虎． 基于改进A*算法和人工势场法智能小车路径规划研究[D]． 西安： 西安电子科技大学， 2020．

［14］武善平， 黄炎焱， 陈天德． 改进A～*算法的水面舰艇静态航路规划[J]． 计算机工程与应用， 2022， 58（23）： 307-315．

［15］赵晓， 王铮， 黄程侃， 等． 基于改进A*算法的移动机器人路径规划[J]． 机器人， 2018， 40（6）： 903-910．

Research on AGV Path Planning Based on Improved A* Algorithm

ZHANG Yameng， WANG Jun， FU Chaoxing

_{o5HoOkW+Mj3csPkGlYi8zA==}

（College of Mechanical and Electrical Engineering， Qingdao University， Qingdao 266071， China）

Abstract：

Aiming at the problems of long search path planning time，low search efficiency and lack of consideration of AGV running volume in the traditional A* algorithm in Automated Guided Vehicle pathfinding，the heuristic factor in the heuristic estimation function is improved by dynamic weighting method，and the weighting value is selected according to the actual path situation．It filters and searches the neighborhood time points，eliminates the direction that is certain to inevitably increase the path generation value，and increase the influence radius of obstacles to avoid collision during AGV navigation．Simulation results show that compared with the original A* algorithm，the number of nodes searching is reduced by 82% and the search time is reduced by 81%，which improves the path planning efficiency．Moreover，the improved A* algorithm considers the safety radius of AGV operation and ensures the safety of AGV operation．Avoid collisions during actual navigation．

Keywords：

A* algorithm； heuristic factor； automated guided vehicle； path planning

收稿日期： 2024-06-10； 修回日期： 2024-07-19

基金项目： 山东省自然科学基金资助项目（ZR2020QE183）

第一作者： 张亚萌（2001-），男，硕士研究生，主要研究方向为人工智能。

通信作者： 符朝兴（1967-），男，博士，副教授，主要研究方向为人工智能和机械振动。Email： cx_f@163.com