基于神经网络的激波抖振特征提取与始发预测

摘 要：激波抖振是一种由激波-边界层干扰引起的激波自激振荡现象，可能导致结构疲劳破坏，甚至引发飞行安全问题。激波抖振始发边界的准确预测对于运输类飞机的设计具有重要的工程意义。本文建立了一个融入定常流场中特征的神经网络（CFNN）模型，实现了对激波抖振始发迎角的准确预测。以 NACA0012 翼型为研究对象，利用卷积神经网络（CNN）模型提取抖振发生前后定常流场中的特征。随后，将提取的低维特征作为全连接神经网络（FNN）模型的隐含层，用以预测激波抖振的始发迎角。在较高马赫数的泛化预测中，CFNN模型预测的激波抖振始发迎角的平均相对误差，相较未融入特征的全连接神经网络（NN）模型，减小了约70%以上。研究结果表明，从定常流场中提取的低维特征能够辅助预测非定常激波抖振问题的始发迎角，提升神经网络模型的性能。

关键词：激波抖振； 定常流场； 特征提取； 边界预测； 卷积神经网络

中图分类号：V219 文献标识码：A DOI：10.19452/j.issn1007-5453.2024.07.005

基金项目： 航空科学基金（2019ZH053003）

激波抖振也称为跨声速抖振，是指在特定的马赫数和迎角组合下发生的激波自激振荡现象。这种现象会引起大幅的升力脉动，并影响飞行器的飞行品质、结构强度和疲劳寿命。因此，对于大型运输类飞机而言，巡航状态与抖振始发边界之间需要一定的裕量，准确识别抖振的始发迎角具有重要意义。

激波抖振是一种非定常、非线性的流动不稳定现象，目前存在着两种主流的激波抖振机理解释。1990年，Lee[1]提出了激波-边界层干扰反馈模型，认为激波处形成的压力波沿边界层向下游传播，在翼型尾缘处由“库塔条件”诱导产生的声波向上游传播，上游传播扰动和激波之间的相互作用形成了一个反馈回路，维持持续的激波运动。Crouch [2-3]从全局稳定性的角度开展了抖振问题的研究，认为激波抖振的产生是由流动全局不稳定性引起的，其特点是Hopf分岔导致的激波与分离边界层的相位锁定。因此，激波抖振的始发边界通常采用非定常方法进行判定。在风洞试验中，通过使用动态压力传感器测量非定常脉动压力或是利用高速纹影技术识别激波位置变化[4-5]，进以确定抖振始发边界，这种手段比较耗时且高昂，难以满足飞机外形优化过程中重复试验的需求a97db9f87286145fb0eea674938de7c6。此外，非定常雷诺平均纳维-斯托克斯方程（URANS）、分离涡模拟（DES）和大涡模拟（LES）等方法[6-9]相继用于激波抖振仿真研究，抖振始发边界可以通过分析压力系数的波动来判定。在这方面，URANS方法因其相对较高的计算效率而得到广泛采用，但这种方法对湍流模型、时间步长和网格密度等都比较敏感，模型需要确定合适的参数，依赖数值仿真经验。除了非定常手段，其余可行的思路是采用定常方法。在风洞试验中，将抖振始发与分离区扩展到后缘的马赫数或迎角联系起来，通过尾缘压力发散方法识别抖振始发。在基于雷诺平均纳维-斯托克斯（RANS）方程[10]进行数值模拟的结果中，激波运动导致升力曲线斜率减小、压力中心位置剧烈变化，被广泛接受作为激波抖振的始发判据。

目前，降阶模型（ROMs）[11-14]通过降低复杂流动系统的阶数，提取其显著特征，成功地建立了高效的非定常模型，成为开展激波抖振机理分析、控制率设计及优化等研究的一项重要手段。这些模型主要分为基于系统辨识方法和基于流场特征提取方法。在非定常气动力建模方面，大量的研究集中于系统辨识方法，而在研究全阶流场的动力学时，更适合采用模态分解技术，以提取主导模态并进行流场的重构和预测。然而，在涉及激波和分离效应的激波抖振问题上，该方法的建模精度较低，预测非线性系统仍然存在问题。

机器学习[15-20]可以对数据进行学习和分析，并拥有强大的非线性函数拟合能力。针对激波抖振涉及强烈的非线性现象，如激波运动和流动分离，该方法具有补充和替代的潜力，其计算成本更低，所需时间更短。Sabater等[17]在预测飞机表面压力分布的研究中证实了这一点，当激波和分离导致流动非线性时，在准确捕获跨声速流动中的激波强度或位置方面，神经网络模型优于高斯过程和本征正交分解结合插值技术的方法。2022年，李记超等[20]提出了一种基于物理的抖振分析数据驱动模型，其中添加了变翼型、马赫数、雷诺数与迎角的148860对二维翼型的训练数据，将压力和摩擦力分布作为输入层，其预测的激波抖振始发迎角的平均绝对误差为0.05°。根据以往的研究结果，纯数据驱动的端到端建模通常需要大量的带标签数据，这些模型在小样本条件下很难泛化到其他新类别。

综上所述，本文建立了一个融入定常流场中低维特征的神经网络（CFNN）模型，其中采用卷积神经网络（CNN）模型对定常流场进行卷积运算与下采样操作，降低数据的维度，提取流场中的特征，随后将提取的特征作为全连接神经网络（FNN）模型的隐含层，输出最不稳定模态的增长率，实现对激波抖振始发迎角的准确预测。

1 流场数据仿真与预处理

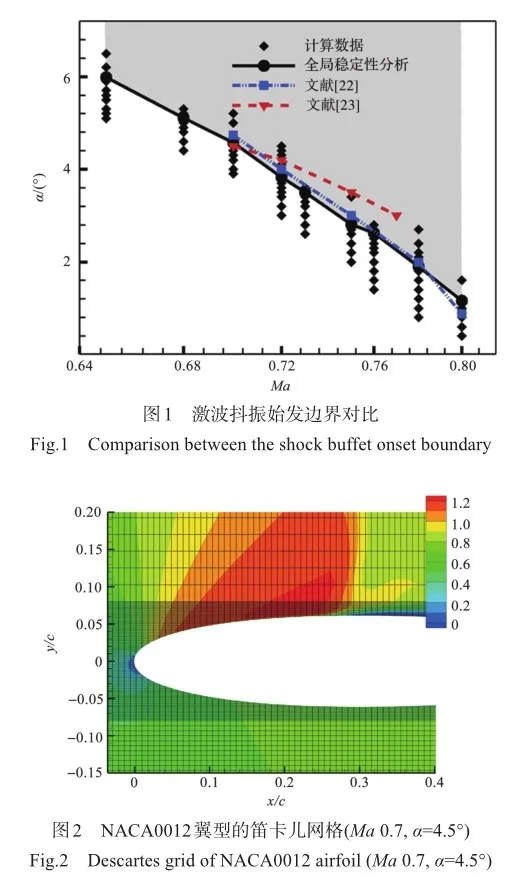
针对NACA0012翼型，本文采用了基于SpalartAllmaras（S-A）湍流模型的URANS求解器[21]开展数值模拟，对应的马赫数范围为0.65～0.80，雷诺数为3′106。高传强等[21]使用相同的计算流体力学（CFD）框架和流场网格验证了NACA0012翼型的激波抖振始发边界与气动力。本文从流动稳定性的角度[2-3]，通过对控制方程进行线性化处理，将对应的全局雅可比矩阵进行特征值分解，进以分析流场的稳定性，其中特征值的实部对应于扰动的增长率，当特征根的实部为正时，意味着流动是不稳定的，特征根的虚部对应于扰动的频率。研究使用了基于全局稳定性分析的求解器，与Doerffer等[22]试验结果和Soda等[23]仿真结果对比，抖振边界与试验结果相近，如图1所示。

根据卷积神经网络的数据格式要求，对弦长c=1的NACA0012翼型附近的混合非结构化网格流场进行数据预处理，将其线性插值转换为分辨率254×256的笛卡儿网格流场。为了保证插值处理后的近壁面流场的准确性，对贴近附面层的网格加密划分了128个单元，如图2所示。

2 激波抖振的特征提取

2.1 CNN模型

卷积神经网络是最早应用于图像处理和模式识别领域的一种深度学习算法，能够自动学习图像中的特征表示，具备强大的表达能力和泛化能力。目前该方法在流体力学领域[15-16，20]得到了广泛探索和研究，适用于多种任务。

本文的CNN模型的建立是基于开源的Python机器学习库Pytorch。每个来流参数下的空间坐标（X， Y）、X和Y方向的速度分量（U， V）与压力p的网格流场作为输入数据，将抖振是否发生作为目标约束，损失函数采用交叉熵误差，具体模型架构如图3所示。

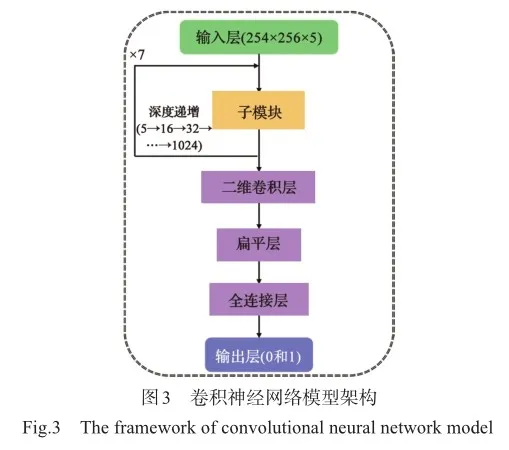
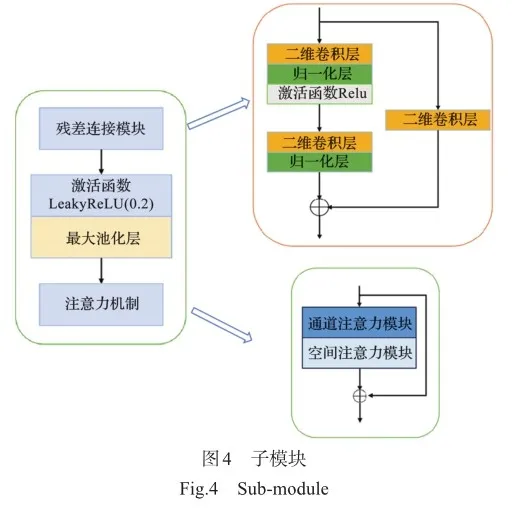
模型中的子模块为残差连接层、最大池化层（下采样操作）与注意力机制层的串联，如图4所示。残差连接避免了梯度消失和梯度爆炸的问题，而注意力机制增强了对关键特征的感知能力。同时通过多层子模块操作，可以学习不同尺度的特征，并降低输入流场数据的维度。在子模块中，二维卷积层的核尺寸为3′3、步幅与填充均为1′1，使用了2′2的最大池化操作，并进行1′1的填充。

此外，模型训练的迭代次数为 100，批量大小设置为 2，采用AdamW优化器以优化反向传播过程，初始学习率取0.001，学习率控制器采用ReduceLROnPlateau模块，衰减因子设置为0.5，根据模型性能自动调整学习率。

2.2 定常流场中特征提取

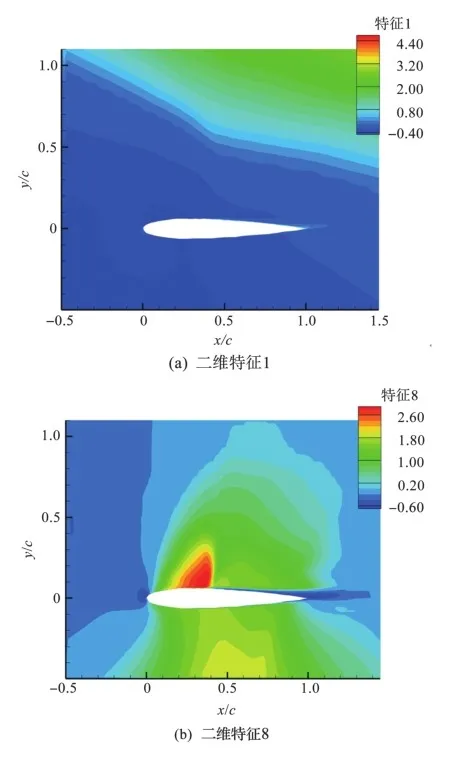
基于CNN模型开展定常流场中特征的提取，对于内插马赫数的激波抖振特征提取与始发迎角预测，将马赫数为0.70、0.76的样本作为训练集，预测马赫数为0.72和0.75的抖振状态。图5展示了定常流场（X， Y， U， V， P）进行第一层子模块操作（流场分辨率减少一半）后生成的部分特征云图，如特征8和特征10主要集中在激波或尾迹区域，而另一些特征（如特征1和特征12）则主要集中在采样边界区域。由此可见，采用CNN模型提取的特征，部分存在物理意义，也存在数值上的特征。

xi5T+AxJwA9WZQ5ApdfaFwMMxsKZTvYS/dite8e4S50=在CNN模型中进行扁平层操作后生成了4个一维特征，这些特征缩放1%倍后，与典型流场特征（如升力系数、增长率、激波位置（激波位置在流场中的最大横坐标）、分离起始位置（流动分离起始的最小横坐标））相比较，如图6所示。特征2与激波位置以及分离起始位置呈现相似的变化趋势。

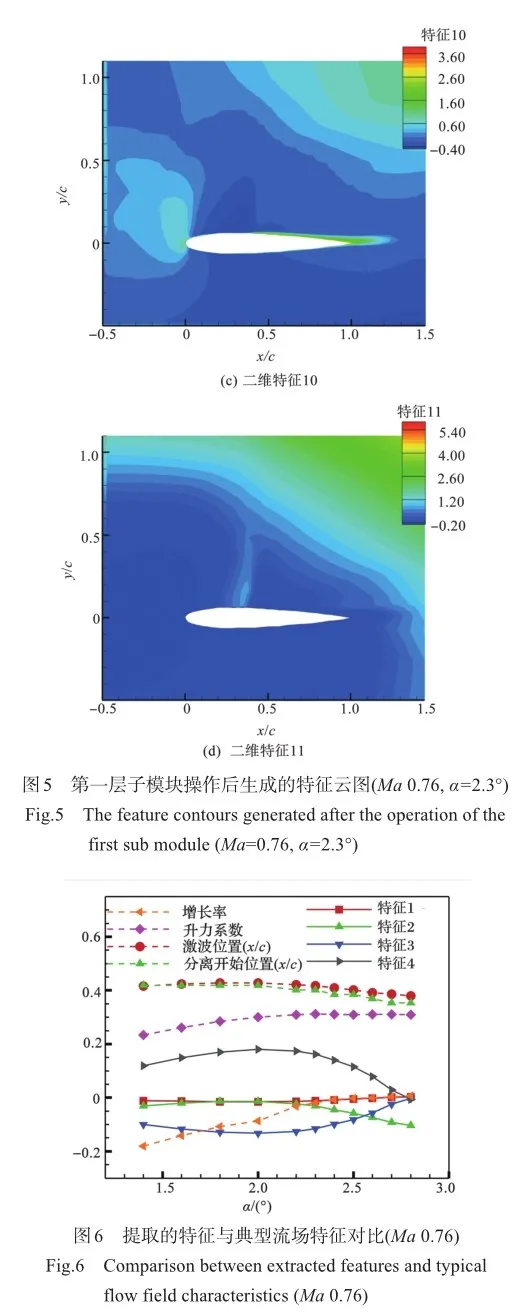
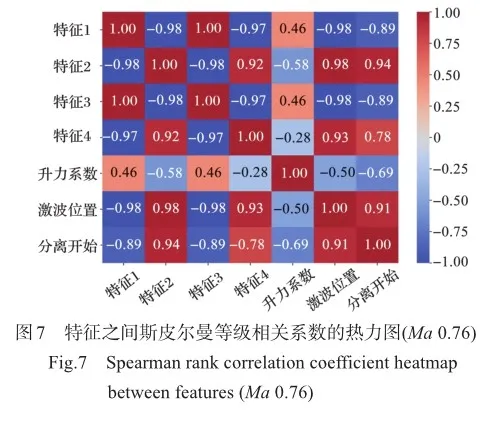
同时，斯皮尔曼相关系数可以有效衡量两个变量之间的单调关系，尤其适用于数据不满足正态分布、包含异常值或对等级顺序关系感兴趣的情况。在特征相关性分析中可知，提取的特征2与激波位置和分离起始位置之间存在较强的相关性，如图7所示。这些特征之间的单调关系显著，与二维的特征云图的分析结果一致。

3 激波抖振始发迎角预测

3.1 融入特征的FNN模型

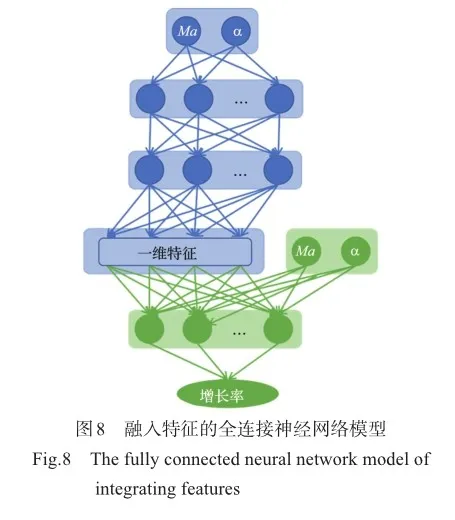
基于定常流场中提取的4个一维特征建立抖振始发迎角预测模型，将提取的特征添加在FNN模型的隐含层，其中输入层为马赫数、迎角，输出层为扰动的增长率，隐含层大小分别为[32，32]、[32]，如图8所示。

为了提高模型的预测精度，首先对输入数据进行了归一化（Min-Max Scaling）处理，以减少特征之间数值差异对模型的影响。然后选择了均方差误差作为损失函数，该损失函数包括了特征误差和增长率误差，从而更全面地评估模型的性能。此外，为了增强模型的非线性拟合能力，采用Leaky ReLU作为激活函数，在输入为负时选择了一个非零斜率为0.2。最后，为了优化反向传播过程，使用AdamW优化器，并设置学习率为0.01，引入ReduceLROnPlateau模块作为学习率控制器，并将衰减因子设置为0.9998。

3.2 抖振始发迎角预测结果

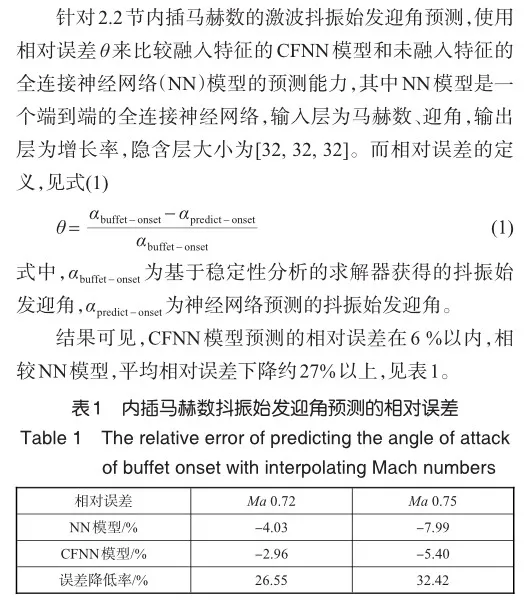
但是对于训练马赫数边界外的抖振始发迎角预测，两种模型均出现较大的预测误差。

3.3 抖振始发迎角外推泛化预测结果

由于实际应用中通常涉及小样本数据，并且激波抖振显著限制了跨声速飞行器的飞行性能边界。因此，提高模型对外插数据预测的准确性是研究的重点，如较高马赫数0.78和0.80。

针对不同马赫数的训练样本设计了一系列不同的算例，以评估CFNN模型在外推泛化方面的能力。同时为了增强数据对称性和模型预测精度，预测马赫数分别为0.78、0.80，另一边界的马赫数自0.68逐渐增大调整到0.73、0.75，与预测马赫数的样本设计保持一致，将这两个马赫数的样本以迎角递增排序，取序列前三的样本与这两个马赫数范围内的所有样本一同作为训练数据构成了训练集。对不同算例的CFNN模型与NN模型的预测结果进行了对比，如图9所示。

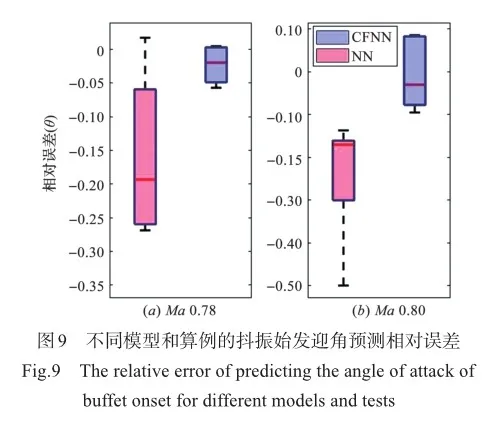
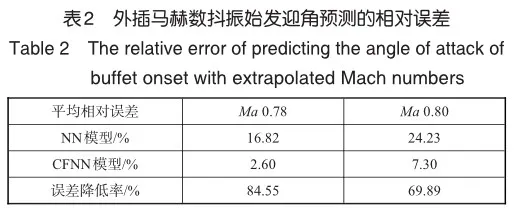
不同算例的平均相对误差，CFNN模型相较NN模型降低了约70%以上，见表2。本文方法通过将提取的定常流场中特征引入神经网络模型，能够更准确地预测抖振始发迎角，并提高模型的泛化性能。

4 结论

本文建立了一个融入定常流场中特征的神经网络（CFNN）模型，采用卷积神经网络模型提取流场中的低维特征，并开展了激波抖振始发迎角的预测。通过研究，可以得出以下结论：

（1）采用CNN模型提取了4个一维特征，其中提取的特征2与激波位置、分离起始位置的相关性较强。可见，通过多层卷积运算和下采样操作，从流场中提取出了部分物理信息。其余特征与物理特征的变化趋势相差较大，可能存在数值上的特征或冗余。

（2）针对CFNN模型， 其内插马赫数抖振始发迎角预测的相对误差在6%以内，相较于NN模型，降低了27%以上。而对于较高马赫数的外推预测，不同算例的抖振始发迎角预测的平均相对误差，CFNN模型相较NN模型降低了70%以上。

综上所述，定常流场中提取的低维特征有利于提高神经网络模型对激波抖振始发迎角预测的准确性与泛化能力。

参考文献

[1]Lee B H K. Oscillatory shock motion caused by transonic shock boundary layer interaction[J]. AIAA Journal， 1990， 28（5）： 942-944.

[2]Crouch J D， Garbaruk A， Magidov D， et al. Origin of transonic buffet on aerofoils[J]. Journal of Fluid Mechanics， 2009， 628： 357-369.

[3]Crouch J D， Garbaruk A， Magidov D. Predicting the onset of flow unsteadiness based on global instability [J]. Journal of Computational Physics， 2007， 224（2）： 924-940.

[4]Jacquin L， Molton P， Deck S， et al. Experimental study of shock oscillation over a transonic supercritical profile[J]. AIAA Journal， 2009， 47（9）：1985-1994.

[5]Hartmann A， Klaas M， Schr？der W. Time-resolved stereo PIV measurements of shock boundary layer interaction on a super‐critical airfoil[J]. Experiments in Fluids， 2012， 52（3）：591-604.

[6]Grossi F， Braza M， Hoarau Y. Prediction of transonic buffet by delayed detached-eddy simulation[J]. AIAA Journal， 2014， 52（10）： 2300-2312.

[7]Szubert D， Grossi F， Garcia A J， et al. Shock-vortex shear-layer interaction in the transonic flow around a supercritical airfoil at high Reynolds number in buffet conditions[J]. Journal of Fluids and Structures， 2015， 55：276-302.

[8]Fukushima Y， Kawai S. Wall-modeled large-eddy simulation of transonic airfoil buffet at high Reynolds number[J]. AIAA Journal， 2018， 56（6）： 2372-2388.

[9]Tahani M， Masdari M， Eivazi H， et al. Assessment of turbu‐lence models for transonic oscillating airfoil[J]. International Journal of Numerical Methods for Heat & Fluid Flow， 2017， 27（11）： 2603-2628.

[10]Chung I， Lee D， Reu T， et al. Prediction of transonic buffet onset for airfoils with separation bubble using steady approaches[J]. Journal of Aircraft， 2003， 40：795-797.

[11]Tang D， Kholodar D， Juang J N， et al. System identification and proper orthogonal decomposition method applied to unsteady aerodynamics[J]. AIAA Journal， 2001， 39（8）： 1569-1576.

[12]Kou Jiaqing， Zhang Weiwei. An improved criterion to select dominant modes from dynamic mode decomposition[J]. European Journal of Mechanics B-Fluids， 2017， 62： 109-129.

[13]Silva W. Identification of nonlinear aeroelastic systems based on the Volterra theory： progress and opportunities[J]. Nonlinear Dynamics， 2005， 39（1-2）： 25-62.

[14]Flinois T L B， Morgans A S. Feedback control of unstable flows： a direct modelling approach using the eigensystem realisation al‐gorithm[J]. Journal of Fluid Mechanics， 2016， 793： 41-78.

[15]Bhatnagar S， Afshar Y， Pan S W， et al. Prediction of aerodynamic flow fields using convolutional neural networks[J]. Computation‐al Mechanics， 2019， 64（2）：525-545.

[16]曹晓峰， 李鸿岩， 郭承鹏，等. 基于深度学习的二维翼型流场重构技术研究[J]. 航空科学技术， 2022， 33（7）： 106-112. Cao Xiaofeng， Li Hongyan， Guo Chengpeng， et al. Research on the reconstruction technology of two-dimensional airfoil flow field based on deep learning [J]. Aeronautical Science & Technology， 2022， 33（7）： 106-112. （in Chinese）

[17]Sabater C， Stürmer P， Bekemeyer P. Fast predictions of aircraft aerodynamics using Deep-Learning techniques[J].AIAA Jour‐nal， 2022， 60（9）：5249-5261.

[18]韩天依星， 皮思源， 胡姝瑶，等. 基于机器学习预测流场特征的网格生成技术研究进展[J]. 航空科学技术， 2022， 33 （7）： 30-45. Han Tianyixing， Pi Siyuan， Hu Shuyao， et al. Research prog‐ress on grid generation technology based on machine learning for predicting flow field characteristics [J]. Aeronautical Sci‐ence & Technology， 2022， 33 （7）： 30-45. （in Chinese）

[19]Wang Xu， Kou Jiaqing， Zhang Weiwei， et al. Incorporating physical models for dynamic stall prediction based on machine learning[J]. AIAA Journal， 2022， 60（7）： 4428-4439.

[20]Li Jichao， He Sicheng， Zhang Mengqi， et al. Physics-based da‐ta-driven buffet-onset constraint for aerodynamic shape optimi‐zation[J]. AIAA Journal， 2022， 60（8）： 4775-4788.

[21]Gao Chuanqiang， Zhang Weiwei， Ye Zhengyin. Numerical study on closed-loop control of transonic buffet suppression by trailing edge flap[J]. Computers & Fluids， 2016， 132： 32-45.

[22]Doerffer P， Hirsch C， Dussauge J P， et al. Unsteady effects of shock wave induced separation [M]. Berlin： Springer Science& Business Media， 2010.

[23]Soda A， Voss R. Analysis of transonic aerodynamic interfer‐ence in the wing-nacelle region for a generic transport aircraft[C]. International Forum on Aeroelasticity & Structural Dy‐namics.DLR， 2005.

Shock Buffet Feature Extraction and Onset Prediction Based on Neural Network

Ma Qiyue1， Gao Chuanqiang1， Sun Jian2

1. Northwestern Polytechnical University， Xi’an 710072， China

2. Beijing Institute of Astronautical Systems Engineering， Beijing 100076， China

Abstract： Shock buffet is a self-excited oscillation phenomenon caused by shock wave-boundary layer interference， which may lead to structural fatigue failure and even cause flight safety issues. The accurate prediction of shock buffet onset boundary is of great engineering significance for the design of transport aircr70a58aff8567aa10aed005d6422442695386c71b5b9fa358a4738004b30f9651aft. This paper establishes a Characteristics-integrated Fully connected Neural Network （CFNN） model that incorporates features from steady flow field， achieving accurate prediction of shock buffet onset angle of attack. Taking the NACA0012 airfoil as the research object， a Convolutional Neural Network （CNN） model extracts features from the steady flow field before and after the onset of the shock buffet. Subsequently， the extracted low dimensional features are used as hidden layers in the Fully connected Neural Network （FNN） model to predict the onset angle of attack of the shock buffet. In the generalization prediction of higher Mach numbers， the average relative error of the shock buffet onset angle of attack predicted by the CFNN model is reduced by more than 70% compared to the fully connected Neural Network （NN） model without incorporating features. The research results indicate that the low dimensional features extracted from the steady flow field can assist in predicting the onset angle of attack for unsteady shock buffet problems and improve the performance of neural network models.

Key Words： shock buffet； steady flow field； feature extraction； boundary prediction； CNN