基于信息熵的鲁棒稀疏子类判别分析

【摘 要】 线性判别分析（Linear discriminant analysis， LDA）作为一种有监督的降维方法，已经广泛应用于各个领域。然而，传统的LDA存在以下缺点：1）LDA假设数据是高斯分布和单一模态的；2）LDA对异常值和噪声十分敏感；3）LDA的判别投影方向对特征的可解释性低且对降维数较为敏感。为克服以上问题，提出了基于信息熵的鲁棒稀疏子类判别分析（Robust sparse subclass discriminant analysis based on information entropy， RSSDAIE）新方法。具体而言，对每个类别划分不同数量的子类后，重新定义类内散射矩阵和类间散射矩阵，使其更适应现实数据。另外，引入[21]范数、稀疏矩阵和正交重构矩阵以确保RSSDAIE具有更高的鲁棒性、更好的可解释性和更低的维度敏感性。同时采用交替方向乘子法对目标函数求解，避免类内散射矩阵不可逆的情形。在多个数据集上进行了对比实验，证明了RSSDAIE在数据适用类型、降低噪声影响、减少降维数影响等方面更有优越性，分类准确率更高。

【关键词】 类内多模态；信息熵；判别分析；[21]范数

Robust Sparse Subclass Discriminant Analysis

Based on Information Entropy

Yang Yuan， Zhou Yuejin*

（Anhui University of Science and Technology， Huainan 232001， China）

【Abstract】 Linear discriminant analysis （LDA）， as a supervised dimension reduction method， has been widely applied in various fields497e4863aa9b2a2daac2978870bc9e8dcbf55e148eab2993e7018902d2054591. However， traditional LDA has the following drawbacks： 1） LDA assumes that the data are Gaussian distributed and unimodal. 2） LDA is very sensitive to outlier and noise. 3） the discriminant projection direction of LDA has low interpretability of features and is sensitive to the number of dimension reduction. In this paper， a novel method called robust sparse subclass discriminant analysis based on information entropy（RSSDAIE） is proposed to solve the above problems. Specifically， to make RSSDAIE more consistent with real data， each class is divided into different subclasses， and the within-class and between-class scattering matrix are redefined. The [21] norm， a sparse matrix and orthogonal reconstruction matrix are also simultaneously introduced to ensure that RSSDAIE has more robustness and interpretability and reduces the dimensional sensitivity. The objective function is solved by the alternating direction multiplier method to avoid the irreversibility of the within-class scattering matrix. Extensive experiments on several datasets prove that RSSDAIE has more superior advantage in adapting to data types， reducing the effect of noise and dimensionality and has higher classification accuracy compared with other related methods.

【Key words】 within-class multimodality; information entropy; discriminant analysis; [21] norm

〔中图分类号〕 TP391.4 〔文献标识码〕 A 〔文章编号〕 1674 - 3229（2024）03 - 0042 - 11

0 引言

在数据的收集过程中数据的维度越来越高，特征工程的重要性日益增加。特征工程［1］是指在高维的数据中提取能代表数据的重要特征，其本质是对原始数据空间进行学习，研究一个低维子空间对原始数据进行表示，从而降低数据的特征个数、提高模型的效率和准确率。在众多方法中，降维［2］是特征工程的主要方法。降维将原数据空间投影到低维子空间，从而解决“维度祸根”问题，通过对降维后的数据进行处理，能够减少计算量、增强模型的效能。

根据是否利用标签信息，降维分为无监督降维方法和有监督降维方法。在无监督降维方法中，常见的有独立成分分析［3］、t分布随机邻居嵌入［4］、流形学习［5］等，其中最典型的是主成分分析（Principal component analysis， PCA）［6］。PCA降维保留数据集中方差贡献大的特征，随着维度的增加，特征的重要性依次递减。有监督降维方法的典型代表是线性判别分析（Linear discriminant analysis， LDA）［7］。LDA充分利用标签信息找到最具判别性的特征，其核心思想是找到一个投影矩阵使同一类别的数据更紧凑、不同类别的数据更分散，即最大化类间散射矩阵（between-class scattering matrix， [Sb]）和类内散射矩阵（with-class scattering matrix， [Sw]）的比值。由于LDA充分利用标签信息后提取的特征具有可判别性，这使得LDA的应用更为广泛。

在LDA的应用过程中，为提升其性能和效率研究者提出了许多相关的变体。Lu等［8］直接对[Sw]进行正则化处理，避免LDA目标函数求解时[Sw]不可逆的情形。Ye等［9］提出了广义不相关的线性判别分析，通过对LDA目标函数进行转换，将[Sb]和[Sw]的比率问题转化为非比率问题的等价形式。Zhang等［10］和Murthy等［11］对[Sb]和[Sw]进行了不同的函数映射，不仅解决了[Sw]不可逆的问题，还扩大了不同类别样本间的距离。虽然这些方法都解决了LDA中[Sw]不可逆的缺陷，但是针对数据的结构和方法的鲁棒性没有进行研究。

LDA的前提假设是数据为单模态的（每个类别中没有集群）并且符合高斯分布，但是在真实的应用数据中，数据往往是多模态的和非高斯分布的。Zhu等［12］提出了子类判别分析（Subclass discriminant analysis， SDA），对每个类别划分了子类后重新定义[Sb]和[Sw]。Gkalelis等［13］进一步提出了混合子类判别分析（Mixture subclass discriminant analysis， MSDA），只针对非高斯分布的类别考虑了子类。Wan等［14］提出了面向可分离性的子类判别分析（Separability oriented subclass discriminant analysis， SSDA）。SSDA通过平均欧式距离最小化为每个类找到最佳子类数量，从不同的层面重新定义了[Sb]和[Sw]。虽然这些方法都考虑了数据的多模态，但仍然无鲁棒性和可解释性。

LDA目标函数本质上是范数的平方，当数据有噪声和异常值时，LDA的投影方向会因异常值和噪声发生严重的偏移，使LDA的性能下降。Nie等［15］提出了[21]范数，对目标函数的[2]范数求和，减少异常值和噪声的影响。Oh等［16］对目标函数施加了[p]范数，可根据数据自身的特点选择不同的[p]值，从而减少异常值和噪声的影响。Liu等［17］对[21]范数增加了阈值，进一步降低了异常值和噪声对投影方向的影响。此外，LDA的投影矩阵是广义特征值分解中最大特征值对应的特征向量，投影矩阵没有稀疏性使得LDA的可解释性差。Clemmensen等［18］和Anzarmou等［19］提出学习一个稀疏判别子空间增加模型的可解释性。Wen等［20］对投影矩阵施加[21]范数并融入了PCA的正交重构思想，不仅提升了鲁棒性而且具有可解释性。Wang等［21］在此基础上考虑数据的局部流形结构提升模型的表现。Li等［22］通过对投影矩阵增加稀疏上界，用交替方向乘子法对目标函数求解并应用递归程序进行贪婪搜索寻找投影矩阵。

为了使模型适用性更广鲁棒性更高，本文提出了一种基于信息熵的鲁棒稀疏子类判别分析（Robust sparse subclass discriminant analysis based on information entropy， RSSDAIE）的新方法。首先，数据是多模态的，通过最小化子类数据分布的信息熵为每个类别寻找最佳子类数量，通过分层聚类方法划分子类。其次，重新定义了类内散射矩阵[Sw]和类间散射矩阵[Sb]。再次，在目标函数中融入PCA的正交重构思想并考虑鲁棒性和稀疏性。最后，通过构造增广拉格朗日函数，用交替方向乘子法对目标函数进行求解。

1 相关介绍

1.1 符号解释

给定数据集[Z=x1，y1，x2，y2，…，xN，yN]，其中[xl∈RD]表示第[l]个样本，[yl∈1，2，…，C]表示第[l]个类标签，[l=1，2，…，N]。[X=x1，x2，…，xN∈RD×N]为特征矩阵，[D]为样本的维度，[N]为样本总量。[x=1N∑Nl=1xl]表示总样本均值。设第[i]类样本中有[Ni]个样本数据，第[i]类的样本均值为[xi=1Ni∑Nih=1xhi]，其中[h=1，2，…，Ni]，[i=1，2，…，C]，[xhi]是第[i]类的第[h]个样本。对于多模态数据，假设[X]的第[i]类样本中有[Ki]个子类且第[i]类的第[j]个子类中有[Nij]个样本数据，第[i]类的第[j]个子类的样本均值为[xij=1Nij∑Nijm=1xmij]，其中[m=1，2，…，Nij]，[j=1，2，…，]

[Ki]，[xmij]是第[i]类的第[j]个子类的第[m]个样本。

1.2 线性判别分析 （LDA）

LDA［7］作为一种具有判别性的有监督降维方法，已经广泛应用于机器学习的各种领域。LDA目标是使数据的类间散射矩阵[Sb]和类内散射矩阵[Sw]的比值最大化，其中[Sb]描述了不同类别之间的分离性，[Sw]描述了同一类别之内的紧凑性。LDA使不同类别的样本距离最大化、同一类别的样本距离最小化，从而找到最佳的投影方向，其目标函数为：

[JW*=maxWtrWTSbWtrWTSwW] （1）

其中，[W∈RD×d]是LDA将原始高维数据投影到低维的投影矩阵，[d（d≤D）]是数据降维后的维数，[Sb]和[Sw]分别为：

[Sb=1Ni=1CNixi-xxi-xT]

[Sw=1Ni=1Ch=1Nixhi-xixhi-xiT]

Ye等［9］已经证明，式（1）等价于式（2）

[W*=argminWTW=IWTSw-λSbW] （2）

其中，[λ>0]是调节参数。

对于LDA目标函数，如果[Sw]可逆，最优解[W*=（w1，w2，…，wd）]为[SwW=λSbW]的前[d]个最小非零特征值对应的特征向量。在得到投影矩阵[W*]后，对任意样本数据[xl∈RD]，通过LDA降维后的样本数据为[xl=W*Txl∈Rd]，[l=1，2，…，N]。

2 基于信息熵的鲁棒稀疏子类判别分析（RSSDAIE）

LDA处理分析单模态数据，即每个类别中没有子类（集群）。但是在现实中，不同的采集方法、观察角度等都会使数据成为多模态的，即每个类中有多个子类。比如，一个人脸（即一个类别）可能呈现出正面视图的子类和侧面视图的子类或戴眼镜的子类和不戴眼镜的子类等。研究文献［23］表明，当数据存在多模态的情形时，同时最大化类间分离性与子类间分离性、最小化类内紧凑性与子类中的紧凑性，能够使模型的性能显著提升，所以本文研究假设数据是多模态的。

2.1 最佳子类数量的确定

对于最佳子类数量的确定，不同的方法有不同的确定标准。SDA基于近邻的聚类方法将每个2CxVo0BDZ3l8iCsSyr9RNA==类划分成不同的子类，用留一测试（leave-one-out-test， LOOT）和快速的稳定准则确定最佳子类数量。MSDA基于峰度和偏度的非高斯标准划分子类，同时也用留一测试和快速的稳定准则确定最佳子类数量。SSDA基于分层聚类方法划分子类，通过可分离性准则确定最佳子类数量。

分层聚类在给定子类数量[K]和数据集的情形下，对子类的划分是固定的，即分层聚类具有稳定性，所以本文仍采取分层聚类方法。对于最佳子类数量的确定，一个好的指标能够衡量子类之间的分离性和子类内部的紧凑性，本文采用基于信息熵的指标衡量。具体而言，如果一个子类的信息熵很低说明子类样本集中在某一个区域，则视为同一子类。如果一个子类的信息熵很高说明子类样本比较分散，则认为它们不是同一子类。该标准的公式定义如下：

[K*i=argminKi1KiEntropyKi] （3）

[EntropyKi=j=1Ki-NijNilog2NijNi] （4）

其中，[NijNi]是指第[i]类中第[j]个子类的样本数量占第[i]类的样本数量的比值。式（3）能够确保给定子类数量[Ki]后，第[i]类的平均信息熵最小。式（4）是第[i]类中每个子类的信息熵之和。每个类别的最佳子类数量[K*i]，[i=1，2，…，C]的详细确认方法如下。

输入：训练数据集[Z=x1，y1，x2，y2，…，xN，yN，]

最大子类数[Kmax]。

步骤1：令[i=1，2，…，C]，计算每个类的样本数据[Xi]和样本数量[Ni]。

步骤2：令[Ki=2，3，…，Kmax]，使用分层聚类算法获取子类。

步骤3：令j[=1，2，…，Ki]，计算子类的样本数据[Xij]和子类数量[Nij]。

步骤4：计算子类的信息熵之和

[EntropyKi=j=1Ki-NijNilog2NijNi]。

步骤5：计算[K*i=argminKi1KiEntropyKi]。

输出：最佳子类数量[K*=（K*1，K*2，…，K*C）]。

上面的步骤用信息熵为每个类找到了最佳子类数量后，用分层聚类方法对每个类划分了子类。值得注意的是，在每个类中寻找最佳子类数量时，[Ki]是从2到[Kmax]，因为本文的前提假设是数据为类内多模态。

2.2 类内散射矩阵和类间散射矩阵的定义

确定每个类的最佳子类数量[K*]后，基于多模态数据需要重新定义类内散射矩阵和类间散射矩阵。

对于类内散射矩阵，不仅要考虑每个类中样本的紧凑性，还要考虑每个子类中样本的紧凑性。一方面，用每个类别中的子类均值和该类别的均值差异衡量类层面的样本点分布，其公式为：

[Sw1=1Ni=1CNij=1K*ixij-xixij-xiT] （5）

另一方面，用每个子类样本点和该子类均值的差异衡量子类层面的样本点分布，其计算公式为：

[Sw2=i=1Cj=1K*im=1Nijxmij-xijxmij-xijT] （6）

本方法的类内散射矩阵为[Sw=Sw1+Sw2]。

对于类间散射矩阵，用每个子类均值和总均值的差异衡量，其公式为：

[Sb=1Ni=1CNij=1K*ixij-xxij-xT] （7）

由于RSSDAIE方法重新定义了类内散射矩阵和类间散射矩阵，结合LDA方法中的类内散射矩阵和类间散射矩阵，本文考虑3种不同的组合，即[（Sb，Sw）]、[（Sb，Sw）]和[（Sb，Sw）]。在接下来的分析过程中以[（Sb，Sw）]为例。

2.3 稀疏性和鲁棒性的考虑

LDA的投影矩阵W是特征值分解中非零特征值对应的特征向量，所以LDA降维后的特征数据可解释性低。另外，LDA对异常值和噪声十分敏感，导致在真实的数据中性能降低。为克服以上的问题，本文进一步对RSSDAIE增加稀疏性和鲁棒性。

首先，根据LDA目标函数的等价形式，RSSDAIE的目标函数为：

[W*=argminWTW=IWTSw-λSbW] （8）

其次，由于[2，1]范数具有行稀疏性，本文对投影矩阵[W]考虑[2，1]范数增加投影方向的可解释性，其目标函数变为：

[minWtrWTSw-λSbW+λ1W2，1] （9）

其中，[λ1]是平衡参数，[ 2，1]是[2，1]范数。

再次，由于PCA降维后的数据能保留主要的特征信息，利用PCA的思想在约束条件中增加正交重构矩阵，从而降低对维度数[d]的敏感性，其目标函数改进为：

[minW，PtrWTSw-λSbW+λ1W2，1 ]

[s.t. X=PWTX，PTP=I] （10）

式（10）的限制条件相当于通过正交重构矩阵[P∈RD×d]，使重构后的特征矩阵[X]尽可能保留主要的特征息。

最后，在真实的应用数据中存在大量的冗余信息和噪声，本文通过引入稀疏矩阵减少噪声带来的负面影响，因此目标函数改进为：

[minW，P，EtrWTSw-λSbW+λ1W2，1+λ2E1 ]

[s.t. X=PWTX+E，PTP=I] （11）

其中，[λ2]是平衡参数，稀疏矩阵[E]表示误差，用来弥补噪声所导致的负面影响，[ 1]是[1]范数。

2.4 目标函数求解

RSSDAIE的目标函数式（11）可以构建增广拉格朗日函数，然后采用交替方向乘子法对增广拉格朗日函数求解。式（11）的增广拉格朗日函数为：

[LW，P，E，Y=trWTSw-λSbW+λ1W2，1+λ2E1][+Y，X-PWTX-E+β2X-PWTX-E2][=trWTSw-λSbW+λ1W2，1+λ2E1][-12βY2+β2X-PWTX-E+Yβ2] （12）

其中，[Y]是拉格朗日乘子，[∙，∙]是矩阵的内积，[β]是惩罚系数，[ ]是范数。对于[W， P， E， Y]的求解采用交替方向乘子法，即将增广拉格朗日函数分解成若干个子问题，然后对每个子问题进行求解。

步骤1：固定[P， E， Y]，更新投影矩阵[W]。拉格朗日函数简化成：

[LW=trWTSw-λSbW+λ1W2，1][ +β2X-PWTX-E+Yβ2] （13）

令[M=X-E+Yβ]，[W2，1]的导数为[H=diag（w12，]

[w22，…，wd2）-1]。令[∂L（W）∂W=0]，则[W]的解为：

[W=2Sw-λSb+λ1H+βXXT-1βXMTP] （14）

步骤2：更新正交重构矩阵[P]。最小化目标函数为：

[minPTP=IM-PWTX2⇔maxPTP=ItrPTMXTW] （15）

式（15）是一个典型的正交普赛克问题［24］，可以通过奇异值分解求解。若[SVDMXTW=USVT]，则[P=UVT]。

步骤3：更新稀疏矩阵[E]。关于[E]的目标函数为：

[minEλ2E1+β2X-PWTX-E+Yβ2] （16）

在式（16）中，令[α=λ2β]，[E0=X-PWTX-E+Yβ]，对式（16）可以采用收缩算子求解［25］，即[E=shrink（E0，α）]。

步骤4：更新拉格朗日乘子[Y]和惩罚系数[β]。[Y]和[β]解分别为：

[Y=Y+βX-PWTX-E] （17）

[β=min ηβ， βmax] （18）

其中，[η]和[βmax]都是常数。

RSSDAIE算法的具体实现步骤如下所示。

步骤1：选择超参数 [W=0；E=0；Y=0；η=]

[1.01；][ βmax=105。]

步骤2：模型初始化

[P=arg minPtrPTSw-λSbP s.t. PTP=I]。

步骤3：更新迭代次数 [t←t+1]。

1.通过式（14）更新[W]

2.通过式（15）更新[P]

3.通过式（16）更新[E]

4.通过式（17）更新[Y]

5.通过式（18）更新[β]

直到达到最大迭代次数或者收敛时停止。

3 实验分析

为了评估RSSDAIE方法的性能，分别在4个UCI数据集和2个图片数据集上应用RSSDAIE进行降维，并与其他相关方法进行比较分析，包括SSDA-1［14］、SSDA-2［14］、SSDA-3［14］、RSLDA［20］、RLDA（ADMM）［22］和RSLDA（ADMM）［22］。在本文提出的RSSDAIE方法中，考虑3种组合，分别为[（Sb，Sw）]、[（Sb，Sw）]和[（Sb，Sw）]。3种组合的方法分别命名为RSSDAIE-1、RSSDAIE-2和RSSDAIE-3。

在实验设置中，RSSDAIE-1、RSSDAIE-2和RSSDAIE-3的最大子类数量[Kmax]在[{2， 3， 4， 5}]中选择，平衡参数[λ1]和[λ2]在[{10-4，10-3，10-2，10-1，1} ]中选择。SSDA-1，SSDA-2和SSDA-3中的最大子类数量[Kmax]在[{2， 3， 4， 5}]中选择。RSLDA中的平衡参数[λ1]和[λ2]在[{10-4，10-3，10-2，10-1，1}]中选择。RLDA（ADMM）的惩罚参数[ρ]和平衡参数[λ]在[{0.1， 0.5， 1， 5}]中选择。RSLDA（ADMM）中的[ρ]和[λ]在[{0.1， 0.5， 1， 5}]中选择，平衡参数[δ]在[{0.01， 0.05， 0.1， 0.5， 1}]中选择。各种参数选择的准则是使分类准确率达到最高。

对各个数据集，随机选择50%的样本作为训练集，其余数据作为测试集。用训练集为每种方法找到最佳投影矩阵[W*]，将[W*]应用在测试集中对数据进行降维，再用最近邻分类器对降维后的数据进行分类，以分类准确率作为评估标准。

3.1 UCI数据集分析

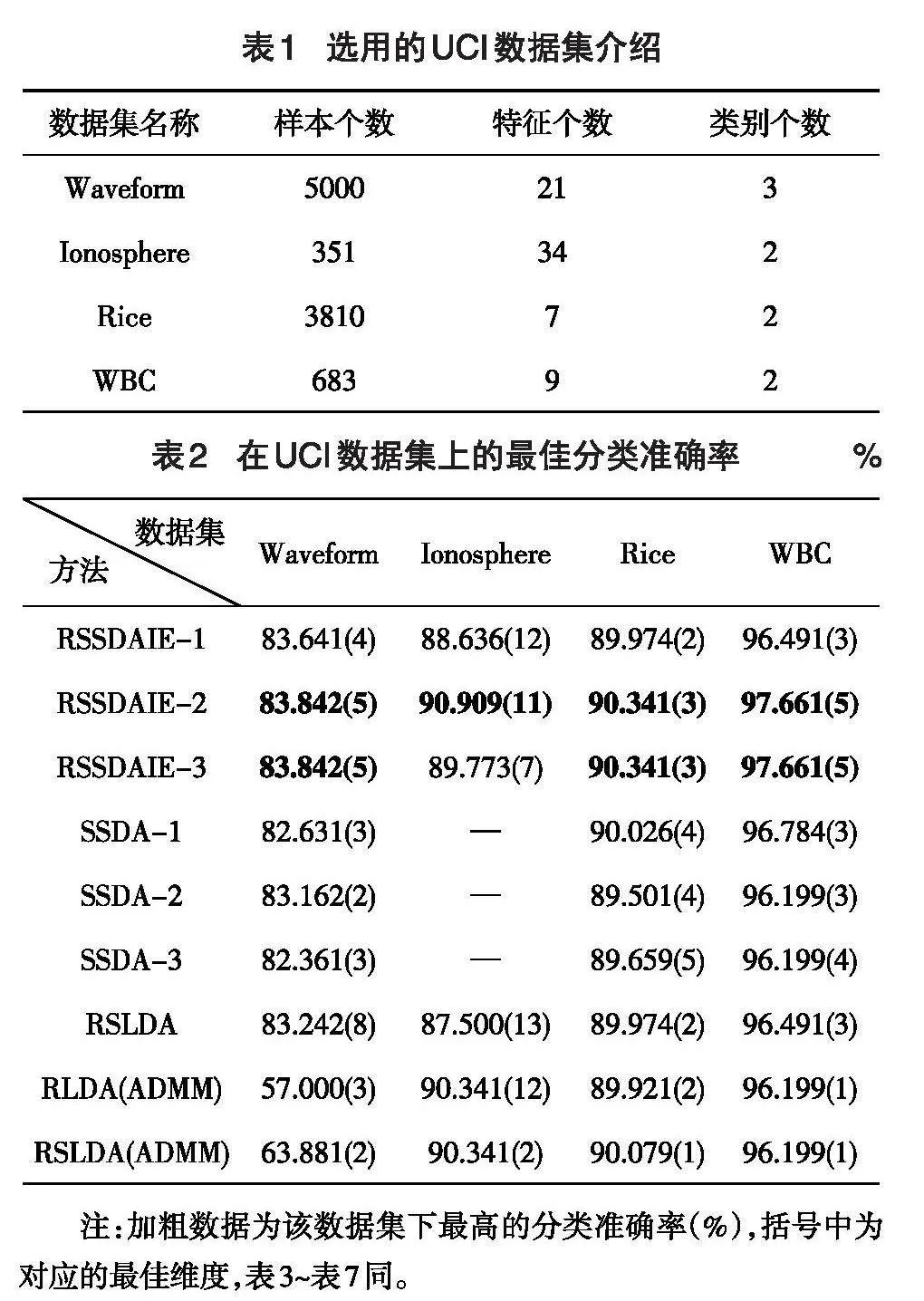
将RSSDAIE-1、RSSDAIE-2、RSSDAIE-3、SSDA-1、SSDA-2、SSDA-3、RSLDA、RLDA（ADMM）和RSLDA（ADMM）应用于UCI数据库中的真实数据集，并进行对比分析。UCI数据库是一个公开的、广泛使用的数据集合，由加州大学欧文分校的计算机科学系维护，从中选择4个数据集进行实验，基本信息如表1所示。

将RSSDAIE-1、RSSDAIE-2、RSSDAIE-3、SSDA-1、SSDA-2、SSDA-3、RSLDA、RLDA（ADMM）和RSLDA（ADMM）应用到表1的数据集中，各种方法的最佳分类准确率和对应的最佳维度如表2所示。

表1 选用的UCI数据集介绍

[数据集名称 样本个数 特征个数 类别个数 Waveform 5000 21 3 Ionosphere 351 34 2 Rice 3810 7 2 WBC 683 9 2 ]

表2 在UCI数据集上的最佳分类准确率 %

[

方法 Waveform Ionosphere Rice WBC RSSDAIE-1 83.641（4） 88.636（12） 89.974（2） 96.491（3） RSSDAIE-2 83.842（5） 90.909（11） 90.341（3） 97.661（5） RSSDAIE-3 83.842（5） 89.773（7） 90.341（3） 97.661（5） SSDA-1 82.631（3） — 90.026（4） 96.784（3） SSDA-2 83.162（2） — 89.501（4） 96.199（3） SSDA-3 82.361（3） — 89.659（5） 96.199（4） RSLDA 83.242（8） 87.500（13） 89.974（2） 96.491（3） RLDA（ADMM） 57.000（3） 90.341（12） 89.921（2） 96.199（1） RSLDA（ADMM） 63.881（2） 90.341（2） 90.079（1） 96.199（1） ][ 数据集]

注：加粗数据为该数据集下最高的分类准确率（%），括号中为对应的最佳维度，表3～表7同。

从表2可以观察到，与其他方法相比较，RSSDAIE-2和RSSDAIE-3的性能更好，两者的分类准确率几乎相同。RSSDAIE-1没有RSSDAIE-2和RSSDAIE-3的分类准确率高，在不同的数据集下它的排名都在中游。在Ionosphere数据集上，由于SSDA-1、SSDA-2和SSDA-3都存在类内散射矩阵不可逆的情形，因此无法运用这3种方法，本文用“—”代替。

为了验证本文方法是否具有更稳健的鲁棒性，在每个数据集的所有样本中，分别随机选择30%或60%的数据加入均值为0、方差为1的高斯噪声，再将RSSDAIE-1、RSSDAIE-2、RSSDAIE-3、SSDA-1、SSDA-2、SSDA-3、RSLDA、RLDA（ADMM）和RSLDA（ADMM）应用在受不同比例噪声污染的数据集中，最佳分类准确率的结果如表3和表4所示。

对比表3和表4，不同的噪声数据中几乎各种方法的分类准确率都降低，但RSSDAIE-2和RSSDAIE-3在多数情况下仍保持最高的分类准确率，RSSDAIE-1的分类准确率也较高。原因是提出的方法对投影矩阵增加了[21]范数并引入了稀疏矩阵以减少噪声的影响。值得注意的是，在表3的Rice数据集中RSLDA（ADMM）无最佳维度对应的最佳准确率，原因是RSLDA（ADMM）出现了不收敛的情形。另外，在表4的Rice数据中，虽然RSSDAIE-1、RSSDAIE-2和RSSDAIE-3的分类准确率一样，但RSSDAIE-1在降维数[d=5]时才能达到84.462%。

表3 具有 30%N （0， 1） 噪声的最佳分类准确率 %

[ 方法 Waveform Ionosphere Rice WBC RSSDAIE-1 78.761（8） 84.091（11） 86.667（5） 97.076（2） RSSDAIE-2 79.169（14） 86.364（13） 88.136（2） 98.246（1） RSSDAIE-3 79.169（14） 86.364（13） 88.136（2） 98.246（1） SSDA-1 77.563（4） 84.091（14） 86.667（2） 97.076（1） SSDA-2 76.821（7） 80.114（14） 86.614（4） 96.784（3） SSDA-3 77.523（7） 79.545（13） 86.457（5） 97.076（2） RSLDA 78.766（8） 83.523（9） 86.667（5） 97.076（2） RLDA（ADMM） 53.962（1） 83.523（5） 86.877（1） 97.076（1） RSLDA（ADMM） 54.165（2） 83.523（3） — 96.199（1） ][数据集]

表4 具有 60%N （0， 1） 噪声的最佳分类准确率 %

[

方法 Waveform Ionosphere Rice WBC RSSDAIE-1 74.768（19） 80.114（10） 84.462（5） 96.784（1） RSSDAIE-2 74.221（11） 82.955（12） 84.462（3） 98.246（3） RSSDAIE-3 74.221（11） 82.955（12） 84.462（3） 98.246（3） SSDA-1 71.801（3） 80.682（10） 83.570（2） 97.953（3） SSDA-2 71.283（3） 74.432（8） 84.199（2） 96.784（2） SSDA-3 71.486（6） 78.977（14） 83.517（2） 97.368（2） RSLDA 74.527（18） 80.114（10） 84.147（5） 96.784（1） RLDA（ADMM） 52.283（3） 76.705（5） 83.045（1） 95.906（1） RSLDA（ADMM） 52.123（2） 77.841（2） 83.675（2） 97.953（1） ][数据集]

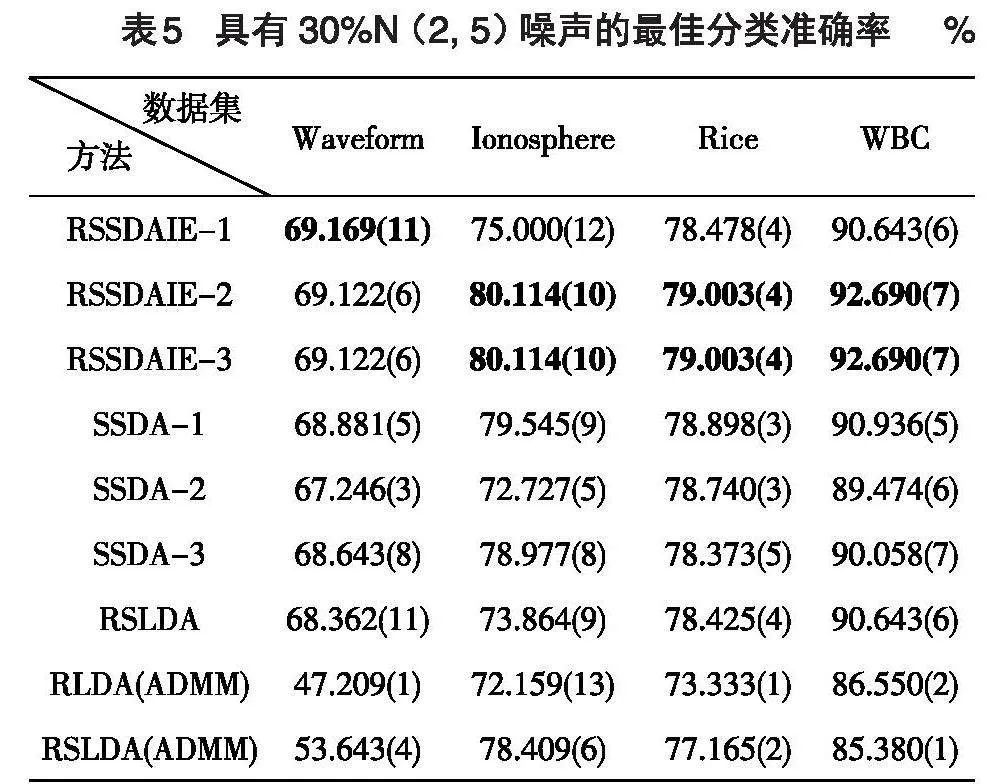
进一步分析不同强度的噪声对各种方法的影响，在4个数据集中分别随机地对所有样本选出30%的数据加入均值为2、方差为5的噪声。在高斯噪声中，均值越大说明噪声的平均水平越高，方差越大说明噪声的波动程度越大。各种方法在该污染数据中的表现如表5所示。

对比分析表3和表5，各数据集都有30%的数据被噪声污染，噪声污染强度越大，各种方法的性能下降越快，而RSSDAIE更具有稳定性。如在Ionosphere数据集上，RSSDAIE-2和RSSDAIE-3的分类准确率仍然保持在80%以上，但其他方法的分类准确率从80%以上跌到80%以下。可见噪声强度越大，本文的方法更具有鲁棒性，性能更加稳定。

表5 具有 30%N （2， 5） 噪声的最佳分类准确率 %

[ 方法 Waveform Ionosphere Rice WBC RSSDAIE-1 69.169（11） 75.000（12） 78.478（4） 90.643（6） RSSDAIE-2 69.122（6） 80.114（10） 79.003（4） 92.690（7） RSSDAIE-3 69.122（6） 80.114（10） 79.003（4） 92.690（7） SSDA-1 68.881（5） 79.545（9） 78.898（3） 90.936（5） SSDA-2 67.246（3） 72.727（5） 78.740（3） 89.474（6） SSDA-3 68.643（8） 78.977（8） 78.373（5） 90.058（7） RSLDA 68.362（11） 73.864（9） 78.425（4） 90.643（6） RLDA（ADMM） 47.209（1） 72.159（13） 73.333（1） 86.550（2） RSLDA（ADMM） 53.643（4） 78.409（6） 77.165（2） 85.380（1） ][数据集]

3.2 图片数据分析

将RSSDAIE的3种组合与SSDA-1、SSDA-2、SSDA-3、RSLDA、RLDA（ADMM）和RSLDA（ADMM）应用于复杂的图片数据中。RSSDAIE-1、RSSDAIE-2和RSSDAIE-3的参数[λ1]和[λ2]根据数据选择最佳数值。RSLDA的参数固定为[λ1=10-4，λ2=10-4]。RLDA（ADMM）的参数固定为[ρ=5]和[λ=0.5]。RSLDA（ADMM）的参数[ρ=5]，[λ=0.5]，[δ=0.1]。对图片数据集降维后的维度[d]在[{10， 20， 30， 40， 50， 60， 70，][ 80， 90，100}]中选择，其他参数与总设置保持一致。

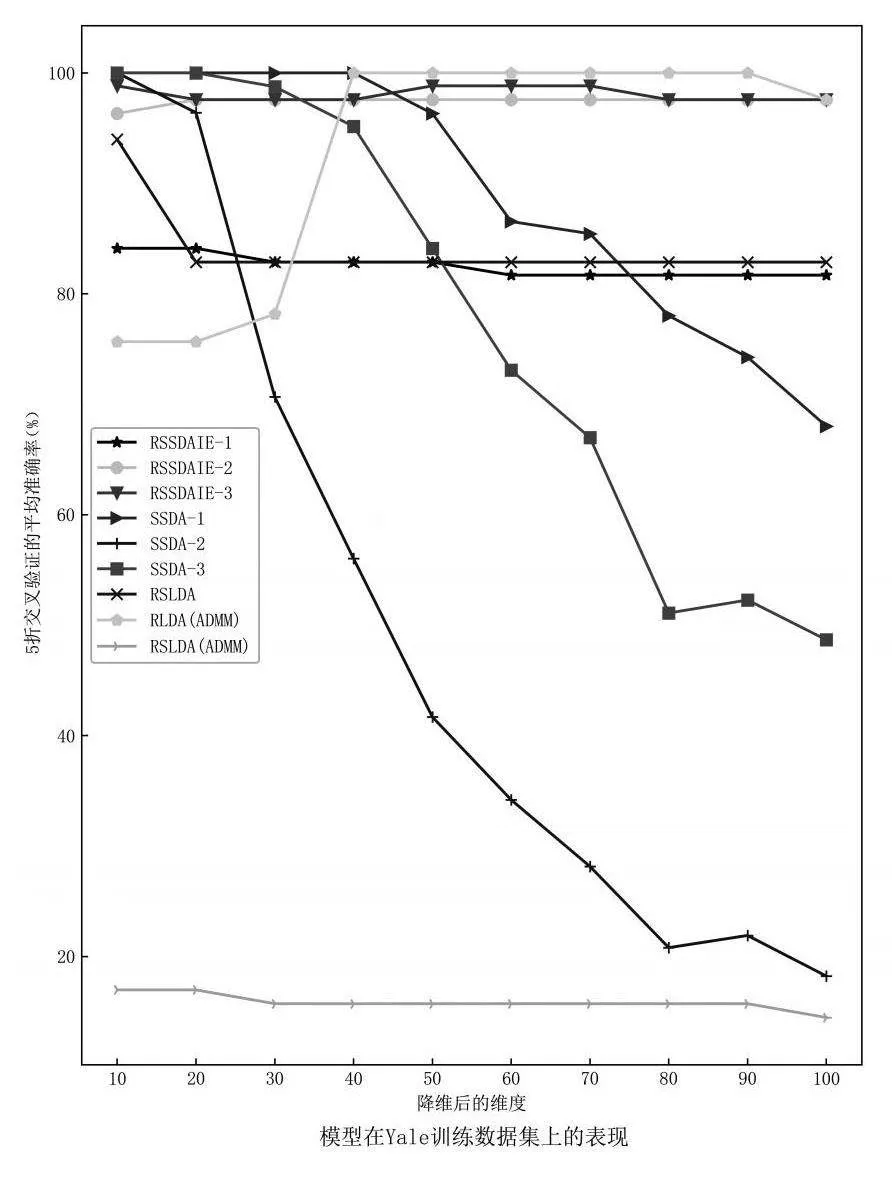
3.2.1 Yale数据集

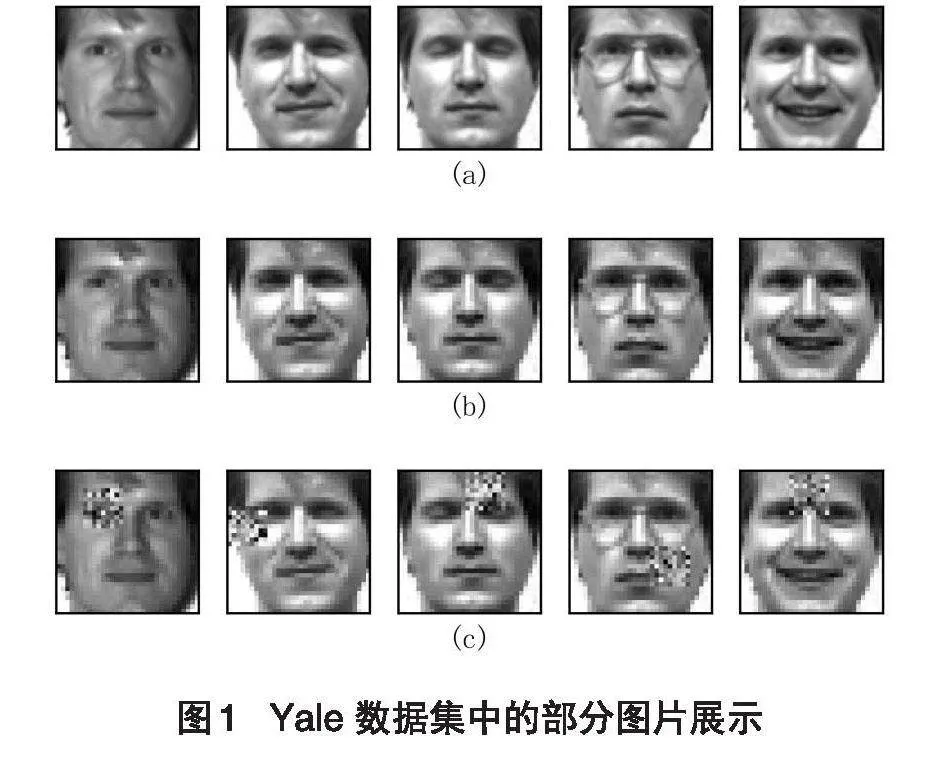
Yale人脸数据集由耶鲁大学创建，包含15个人，每个人在不同表情、姿态和光照下进行拍照，共165张图片，每张图片大小为[100*100]。图1（a）展示了Yale数据集的部分图片。在图1（a）中，图片全部来自于同一个人（同一个类别），有戴眼镜的照片和没戴眼镜的照片，数据可以被视为是多模态的。

图3 不同方法在Yale原数据上的表现2

3.2.2 Coil-100数据集

Coil-100数据集中有100个不同物体的360°旋转图片，每隔5°拍摄一张图片，每个物体都有72张不同角度的图片。Coil-100数据集共有7200张图片，每张图片的大小为[128*128]。根据Coil-100数据集的收集方式，在一定的角度区间可视为同一子类。和Yale数据集的处理方式一样，把Coil-100数据集中的每一张图片进行灰度化，图片大小重置为[32*32]，把图片矩阵转化为维度是1024的图片向量然后进行归一化，将该数据集称为Coil-100原数据集。

RSSDAIE-1、RSSDAIE-2和RSSDAIE-3的平衡参数[λ1]和[λ2]在[{10-4，10-3，10-2，10-1，1}]中进行选择，不同的[λ]值在Coil-100数据上对应的分类准确率如图4所示。通过观察图4，将RSSDAIE-1中的参数[λ1]和[λ2]固定为[10-4]，RSSDAIE-2和RSSDAIE-3的[λ1]和[λ2]固定为[10-2]。

在Coil-100原数据集中加入不同程度的高斯噪声，各种方法的表现如表7所示。

由表7可知，在Coil-100原数据集中，RSSDAIE-3的分类准确率最高，在[d=50]时准确率达到98.028%。RSSDAIE-1和RSSDAIE-2的表现仅次

图5 不同方法在 Coil-100 数据集上的表现

由图5可知，随着维数[d]不断增加，各种方法的分类准确率也不断增加，但增加到一定程度时，分类准确率增长趋于平缓，RSSDAIE-2和RSSDAIE-3在各个维度下都保持最高的分类准确率且分类准确率的极差最小，主要原因是在目标函数中加入了正交重构思想，重构的特征矩阵的主要信息集中在前面的维度中。另外，在Coil-100原数据集上，RSSDAIE-1与RSLDA在[d<80]时，分类准确率差距不大，但在[d≥80]后，RSSDAIE-1比RSLDA表现好。在加入30%N（2，5）噪声后，RSSDAIE-1与RSLDA的表现几乎没有差距。主要是因为RSSDAIE-1考虑的是[（Sb，Sw）]组合，两种算法仅有类间散射矩阵不同，故这两种方法性能相当。RSSDAIE-2和RSSDAIE-3对类内散射矩阵考虑了类层面和子类层面的紧凑性，更符合数据中多模态的特点，这两种方法的表现比其他方法好。

4 总结

本文主要研究了一种基于信息熵的鲁棒稀疏子类判别分析（RSSDAIE），该方法将子类多模态、PCA重构思想、[21]范数和稀疏表示集成到一个模型框架之中。首先，RSSDAIE基于分层聚类方法为每个类别划分不同的子类，通过最小化信息熵确定最佳子类个数。其次，RSSDAIE利用[21]范数的行稀疏性和鲁棒性约束投影矩阵，不仅可以让模型选择最具有判别性的投影方向、减少噪声的影响，而且投影方向更加具有可解释性。再次，RSSDAIE为了保留原特征矩阵中的主要信息，引入PCA的重构思想，给模型加入了一个正交约束项，保证了数据信息损失最小。RSSDAIE也通过引入稀疏误差项来提高对噪声的抵抗性，从而使模型更加具有鲁棒性。最后，RSSDAIE通过构建增广拉格朗日函数，采用交替方向乘子法对目标函数求解，使得模型的收敛速度快。在实验分析中，为了验证提出的RSSDAIE方法在不同散射矩阵下的性能，基于原LDA的类内散射矩阵和类间散射矩阵，以及本文定义的类内散射矩阵和类间散射矩阵，划分了3个不同的子方法，分别为RSSDAIE-1、RSSDAIE-2和RSSDAIE-3。在基础数据集和图片数据上的实验结果表明，本文提出的RSSDAIE-2和RSSDAIE-3的性能相似，比RSSDAIE-1好。RSSDAIE仍有很大的提升空间，在未来的工作中会着重于使RSSDAIE能自适应地为不同的数据集选择最合适的参数值从而提升模型的效率和准确率。

［参考文献］

［1］ Mahajan S， Pandit AK. Analysis of high dimensional data using feature selection models［J］. International Journal of Nanotechnology， 2023， 20（1）：116-128.

［2］ Jia WK， Sun ML， Lian J， et al. Feature dimensionality reduction： a review［J］. Complex and Intelligent Systems， 2022， 8（3）：2663-2693.

［3］ Hao ZY， Jin Y， Yang C. Study of engine noise based on independent component analysis［J］. 浙江大学学报（a卷英文版）， 2007， 8（5）：772-777.

［4］ Kimura M. Generalized t-SNE through the lens of information geometry［J］. IEEE Access， 2021， 9：129619-129625.

［5］ Gashler M， Ventura D， Martinez T. Manifold learning by graduated optimization［J］. IEEE Transactions on Systems， Man and Cybernetics Part B， Cybernetics， 2011， 41（6）：1458-1470.

［6］ Turk M， Pentland A. Eigenfaces for recognition［J］. Cognitive Neuroscience， 1991， 3（1）：71-86.

［7］ Fisher RA. The use of multiple measurements in taxonomic problems［J］. Annals of Eugenics， 1936， 7（2）：179-188.

［8］ Lu J， Plataniotis KN， Venetsanopoulos AN. Regularization studies of linear discriminant analysis in small sample size scenarios with application to face recognition［J］. Pattern Recognition Letters， 2005， 26（2）：181-191.

［9］ Ye J， Janardan R， Li Q， et al. Feature reduction via generalized uncorrelated linear discriminant analysis［J］. IEEE Transactions on Knowledge & Data Engineering， 2006， 18（10）：1312-1322.

［10］ Zhang TP， Fang B， Tang YY， et al. Generalized discriminant analysis： a matrix exponential approach［J］. IEEE Transactions on Systems， Man and Cybernetics Part B， Cybernetics， 2010， 40（1）：186- 197.

［11］ Murthy KR， Ghosh A. Noisy-free length discriminant analysis with cosine hyperbolic framework for dimensionality reduction［J］. Expert Systems With Applications， 2011， 81：88-107.

［12］Zhu Manli， Aleix M. Subclass discriminant analysis［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2006， 28（8）：1274-1286.

［13］ Gkalelis N， Mezaris V， Kompatsiaris I. Mixture subclass discriminant analysis［J］. IEEE Signal Processing Letters， 2011， 18（5）：319-322.

［14］ Wan H， Wang H， Guo GD， et al. Separability-oriented subclass discriminant analysis［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2018， 40（2）：409-422.

［15］ Nie F， Huang H， Cai X， et al. E icient and robust feature selection via joint[2，1]-norms minimization［A］. Advances in Neural Information Processing Systems 23： 24th Annual Conference on Neural Information Processing Systems 2010［C］. British Columbia， Canada： Curran Associates Inc， 2010， 23：1813-1821.

［16］ Oh JH， Kwak N. Generalization of linear discriminant analysis using p-norm［J］. Pattern Recognition Letters， 2013， 34（6）：679-685.

［17］ Liu JK， Xiong X， Ren PW， et al. Capped norm linear discriminant analysis and its applications［J］. Applied Intelligence， 2023， 53（15）：18488-18507.

［18］ Clemmensen L， Hastie T， Witten D， et al. Sparse discriminant analysis［J］. Technometrics， 2011， 53（4）：406-413.

［19］ Anzarmou Y， Mkhadri A， Oualkacha K. Sparse overlapped linear discriminant analysis［J］. Test， 2022， 32（1）：388-417.

［20］ Wen J， Fang XZ， Cui JR， et al. Robust sparse linear discriminant analysis［J］. IEEE Transactions on Circuits and Systems for Video Technology， 2019， 29（2）：390-403.

［21］ Wang JJ， Liu ZH， Zhang KB， et al. Robust sparse manifold discriminant analysis［J］. Multimedia Tools and Applications， 2022， 81（15）：20781-20796.

［22］ Li CN， Shao YH， Yin WT， et al. Robust and sparse linear discriminant analysis via an alternating direction method of multipliers［J］. IEEE Transactions on Neural Networks and Learning Systems， 2020， 31（3）：915-926.

［23］ Wan H， Wang H， Liu J， et al. Within-class multimodal classification［J］. Multimedia Tools and Applications， 2020， 79（39）：29327-29352.

［24］ JMFT Berge. Orthogonal procrustes rotation for two or more matrices［J］.Psychometrika， 1977， 42（2）：267-276.

［25］ Candes EJ， Li XD， Ma Y， et al. Robust principal component analysis［J］. Journal of the Acm， 2011， 58（3）：11-48.

责任编辑 孙 涧

［收稿日期］ 2024-03-20

［基金项目］ 深部煤矿采动响应与灾害防控国家重点实验室基金资助项目（SKLMRDPC22KF03）

［作者简介］ 杨源（1997- ），女，安徽理工大学数学与大数据学院硕士研究生，研究方向：数据处理和降维算法。

［通讯作者］ 周跃进（1977- ），男，博士，安徽理工大学数学与大数据学院教授，研究方向：统计机器学习和高维数据分析。