电涡流位移传感器的仿真分析与验证

【欢迎引用】 黄瑞， 张晓亮， 谢依文. 电涡流位移传感器的仿真分析与验证[J]. 汽车文摘，2024（XX）： X-XX.

【Cite this paper】 HUANG R， ZHANG X L， XIE Y W. Simulation analysis and verification of eddy current displacement sensor[J]. Automotive Digest （Chinese）， 2024（XX）： X-XX.

【摘要】为了研究基于印制电路板（PCB）设计的电涡流位移传感器结构参数对性能的影响，应用Ansys仿真软件，建立电涡流位移传感器模型，分析传感器的线圈激励频率、线圈与被测目标间隙等参数对系统等效阻抗以及感应电压的影响。根据优化模型制作传感器样机，搭建试验平台，将仿真结果与实测结果进行误差分析，试验结果表明，经优化后的系统在全量程范围内的误差达到±1.5%，验证了模型的准确性和可行性，对电涡流位移传感器的开发应用提供了理论依据。

关键词：电涡流感应；位移测量；Ansys；激励频率；PCB线圈

中图分类号：TP212 文献标志码：A DOI： 10.19822/j.cnki.1671-6329.20240013

Simulation Analysis and Verification of Eddy Current Displacement Sensor

Huang Rui，Zhang Xiaoliang，Xie Yiwen

（Schaeffler Intelligent Driving Technology （Changsha） Co.， Ltd.， 410000）

【Abstract】 In order to study the impact of structural parameters of eddy current displacement sensor based on Printed Circuit Board （PCB） design on performance， this paper utilizes Ansys simulation software to establish a model of the eddy current displacement sensor. It analyzes the influence of various parameters， including coil excitation frequency and the gap between the coil and the measured target， on the system’s equivalent impedance and induced voltage. Based on the optimized model， a sensor prototype is constructed， and an experimental platform is established. An error analysis is conducted to compare the simulation results with the measured results. The experimental results show that the error of the optimized system reaches ±1.5% in the full range， thereby verifying the accuracy and feasibility of the model. This study provides a theoretical foundation for the development and application of the eddy current displacement sensors.

Key words： Eddy current induce， Displacement sensor， Ansys， Excitation frequency， PCB coils

0 引言

基于印制电路板（Printed Circuit Board， PCB）设计的电涡流位移传感器具有灵敏度高、结构简单、输出阻抗小、抗干扰能力强及测量精度高等优势，在许多工业生产和控制领域得到广泛应用[1-2]。在电涡流传感器检测和应用前期，一般需要通过多次试验进行不断修正，且在更换不同的量程或者结构时，需要重新测试，延长了试制时间。对于高精度的应用设备，更可靠、更快速的分析方法才能满足其要求。

基于PCB设计的传感器厚度小、易于集成、安装方便。电涡流位移传感器由一个发射线圈（Tx线圈）和至少2个接收线圈（Rx-sin线圈和Rx-cos线圈）以及导电材料制成的被测目标和用于测量、解调和放大线圈信号的信号处理电路组成。当Tx线圈流过高频交变电流，在Rx线圈内部产生交变磁场H1，当没有移动元件存在时，感应电压相互抵消。当被测目标在线圈上移动时，则在被测目标体表面产生电涡流，根据Lenz定理，被测目标上的电涡流产生交变磁场H2，H2方向与H1方向相反，由于磁场H2的反作用使感应线圈中的电流大小和相位都发生了变化，即线圈的等效阻抗发生变化，用线圈等效阻抗的变化来反应被测目标的涡流效应，得到被测目标的位置与感应电压的关系[3-5]。由于等效阻抗的变化受线圈的激励频率、线圈与被测目标的间隙等影响；其次机械误差、加工精度等无法满足输出一致性要求，使其未能得到很好应用。本文基于Ansys建立传感器模型，对传感器系统进行等效电路分析，精确快速地得到被测目标与线圈结构参数的关系。可有效减少试验过程、缩短研制周期，为设计传感器提供理论支撑。

1 传感器建模分析

传感器线圈系统可以等效建模为变压器电路，为了简化，将通过交变电压源代替Tx线圈的振荡器作为驱动电路，Rx线圈中2组或多组线圈幅值一样，具有相位差，本文以2组Rx线圈为例，相位差为90°。Rx线圈和Rx线圈作为变压器原边，被测目标中的涡流电路看作副边，等效电路如图1所示。

图中UTX为激励电压源，R1和L1为激励线圈阻抗和电感，R2和L2为感应线圈阻抗和电感，R3和L3为被测目标物阻抗和电感，M12、M13、M23分别为Tx线圈与Rx线圈、Tx线圈与被测目标、Rx线圈与被测目标的互感系数，其中当传感器确定时，M为一个常数。根据基尔霍夫定律有[6]：

[UTX=I1R1+jωL1-I2jωM12-I3jωM13URX=I2R2+jωL2-I1jωM21-I3jωM230=I3R3+jωL3-I1jωM31-I3jωM32] （1）

式中：[UTX]为交变电压，URX为感应电压，I1为交变电流，I2、I3为感应电流，M为互感系数，L为电感值，R为电阻，[ω]为交变电流频率。

Tx线圈和Rx线圈互感系数很小，可以忽略不计，根据互感的互易定理有[7， 11]：

[M12=M21=0M13=M31M23=M32] （2）

由于Rx线圈作为电压测量的放大级输入，而放大级的输入具有高阻抗性，因此通过Rx线圈的电流几乎为0。且Rx线圈和Tx线圈之间的相互耦合为0，只需求出Tx线圈和被测目标之间的阻抗[8-11]，由式（1）和式（2）所得等效阻抗为：

[Z=UTXI1=R1+ω2M13∙R3R23+ω2∙L23+jωL1-ω2∙M213∙L3R23+ω2∙L23] （3）

得出线圈的等效电阻Req和等效电感Leq为：

[Req=R1+ω2M13R3R23+ω2L23Leq=L1-ω2M13L3R23+ω2L23] （4）

由式（3）、式（4）可知，等效阻抗主要受Tx线圈电阻R1、被测目标与线圈间的互感系数M13、被测目标电阻R3、以及被测目标感抗L3影响。

随着被测目标与Tx线圈间的间隙增大，M13发生变化，导致等效电阻Req和等效电感Leq变化，根据互感系数计算公式[12]得出M：

[M=K/L1∙L2] （5）

式中：K为耦合系数，与线圈和被测目标间的距离有关，距离越大，耦合系数K越小。当Tx线圈和Rx线圈参数一定时，线圈等效阻抗的实部与虚部都是关于耦合系数K的函数[12]。

根据式（3）、式（4），可以计算Rx线圈的感应电压：

[URX=M13∙I3-L1I1M23-L1∙I1I3∙UTX] （6）

在工作频率范围内，控制其他变量时，Tx线圈与被测目标间的互感系数为常数，URX与UTX建立线性关系。

PCB型电涡流传感器匝数一般较少，当在匝数为Ni的激励线圈中通入交变电流i时，Rx线圈中输出感应电动势为：

[e=-N0dφdt=-N0d（lNiiG）dt=-N0NiGldidt] （7）

式中：N0为感应线圈匝数，Ni为激励线圈匝数，l为线圈长度，G为气隙磁导率。

当被测目标在线圈上移动时，电感和电阻会发生变化，线圈的常用衡量参数品质因数Q为：

[Q=2πfLR=2πfL1-ω2M13L3R23+ω2L23R1+ω2M13R3R23+ω2L23] （8）

式中：Q为品质因数，在电涡流的作用下，线圈的阻抗的虚数部分和实数部分发生了变化，引起了Q值的变化。随着被测目标与线圈相对位置的变化，线圈的M值也随之变化，从而导致电感Leq、线圈阻抗Z以及品质因数Q的变化，激励线圈在高频工作，可以提高Q值，降低功耗，增大响应带宽。

在激励线圈中通入正弦交流信号eTX（t）为：

[eTXt=Umsinωt=Umsin2πft] （9）

式中：Um为激励信号幅值。当通入激励信号后，在2组Rx线圈中可获得同频率、不同相位的2组感应电压值。

[e1t=U1sinωte2t=U2cosωt] （10）

式中：U1、U2分别为2组Rx线圈感应电压幅值，而sinωt和cosωt是正交函数，将采集的幅值通过信号处理和位移解析方法，得到传感器的测量位移。

在建立涡流传感器几何模型前，根据模型的结构形状、尺寸以及工况条件的复杂性，需对模型进行结构形式的简化、变化和处理，简化处理后的模型如图2所示。

根据理论分析，传感器线圈匝数N、气隙磁导率G、频率f会改变Q值。Rx线圈和被测目标为传感器的感应部分，对线圈尺寸和匝数进行优化，使灵敏度最大化。减小模型中线圈的走线带来的分布电容、噪声，提高Rx线圈对称度，减小线圈带来的误差。

2 Ansys有限元法建模

Ansys Maxwell是一款低频电磁场仿真软件，使用高精度的有限元方法来解算稳态、频域和时变电磁场和电场，可有效地分析电涡流位移传感器的特性[13]。

在设置网格密度并划分网格时，需要考虑被测目标表面的趋肤效应[14]。其中，被测目标的趋肤深度公式为：

[δ=1μ0μrπσf] （11）

式中：δ为趋肤深度，μ0为真空磁导率，μr为相对磁导率，ƒ为线圈的激励频率，σ为被测导体的电导率。

由式（11）可知，信号频率、电导率和磁导率会影响被测目标的趋肤深度。基于PCB设计的线圈一般由铜线组成，设置被测目标材料为steel-1008，空气域的材料选择为空气，各个材料的电导率σ、相对介电常数μr以及相对磁导率G见表1。

在Ansys中软件中，选择涡流场，设置激励线圈匝数和感应线圈都为4匝，线圈激励为5 V的电压信号。在设定网格大小时应小于相应的趋肤深度值，而被测目标的趋肤深度越大，设定网格越小。选择线圈和被测目标的最大网格为1 mm，空气域为20 mm，此时结果收敛，网格划分如图3所示。

当高频交变电流通过被测物体时，横截面上电流密度不是均匀分布的，而是被测目标表面电流密度大，中心电流密度小，电流密度随被测目标的距离增加而减小，从表面至中心的变化规律为：

[JX=J0∙e-xπfμσ] （12）

式中：J0为被测目标表面的涡流密度，JX为至被测目标表面x深处的涡流密度，μr为被测导体相对磁导率，f为线圈的激励频率，σ为被测导体的电导率。涡流密度的不同代表在表层以下不同深度将以不同的程度改变被测目标的阻抗，表层以下所产生的信号幅值和表面上所产生的涡流不同。

3 仿真结果分析

根据式（11）、式（12），Tx线圈中激励频率对被测目标内部产生的涡流大小及涡流的趋肤深度呈几何倍数增大。感应电流密度越大，说明电涡流位移传感器灵敏度高，当激励振荡频率分别设为100 Hz、1 kHz、10 kHz、100 kHz、1 MHz、10 MHz时，被测目标在不同频率下的涡流密度如图6所示。

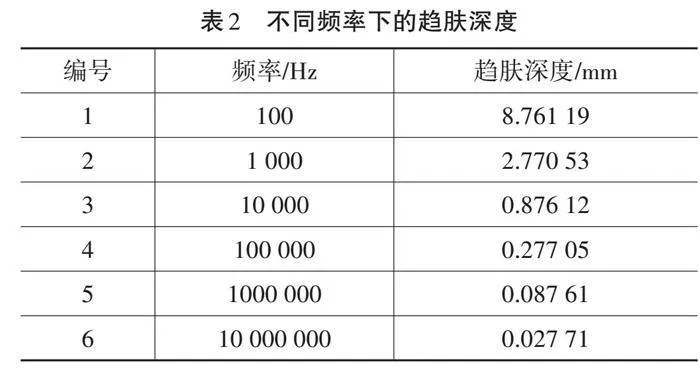
由式（11）可知，当被测目标固定时，电导率和磁导率为定值，趋肤深度只与频率有关，图4中涡流密度J随频率的增大而增大，涡流密度越大对应传感器灵敏度越高。在不同频率下的趋肤深度，如表2所示。

在涡流的作用下，感应线圈的电流幅值和相位发生相应变化，在不同位置得到相应的感应电压值。再经过后续电路采样处理得到线圈位置与感应电压的线性关系。为使线圈灵敏度高，频率应高于1 MHz才能满足高精度要求。

电涡流传感器在进行位移检测时，被测目标与线圈间的互感系数受被测目标与线圈间隙（设为gap）影响，为更精确得到传感器特征参数，选取在不同的线圈位置，即被测目标中心线对应位置分别为0 mm、30 mm、60 mm，由于线圈关于中点左右对称，只需要对左半部分进行仿真即可。被测目标在30 mm位置示意图见图5。

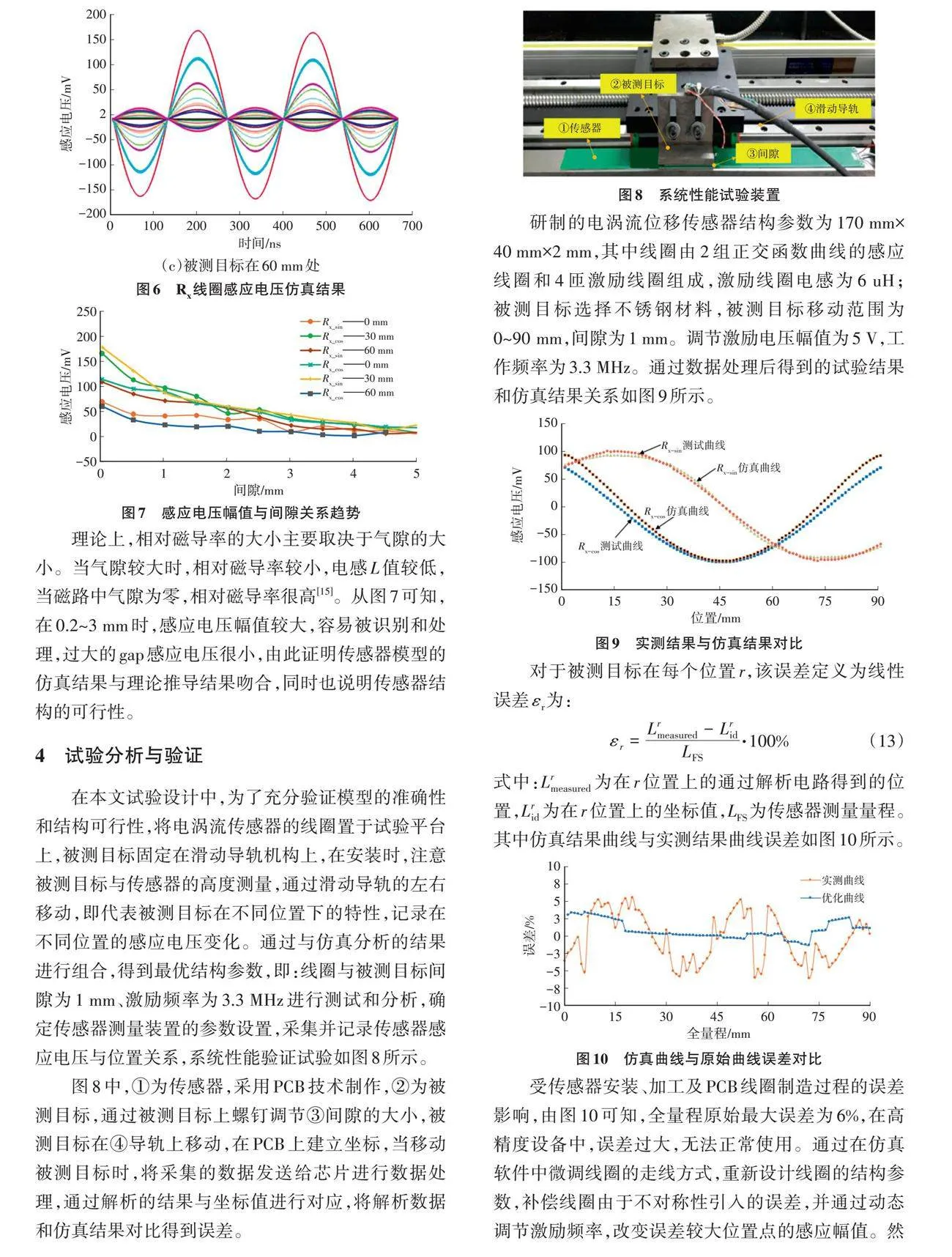
在仿真中，对间隙（gap）进行参数化扫描，gap范围为0.2～10 mm，设置仿真步长为0.1 mm，受线圈本身影响，当gap>10 mm下感应电压很小，几乎可以忽略不计。当在Tx线圈中通入式（9）的激励信号时，设幅值为5 V，频率为3.75 MHz，得到在0 mm、30 mm、60 mm下的Rx-sin和Rx-cos线圈的感应电压值（见图6）。

该正弦曲线符合式（9）、式（10）的理论推导。根据鉴幅工作原理，获取Rx线圈的感应正弦曲线的幅值，如图7所示。

理论上，相对磁导率的大小主要取决于气隙的大小。当气隙较大时，相对磁导率较小，电感L值较低，当磁路中气隙为零，相对磁导率很高[15]。从图7可知，在0.2～3 mm时，感应电压幅值较大，容易被识别和处理，过大的gap感应电压很小，由此证明传感器模型的仿真结果与理论推导结果吻合，同时也说明传感器结构的可行性。

4 试验分析与验证

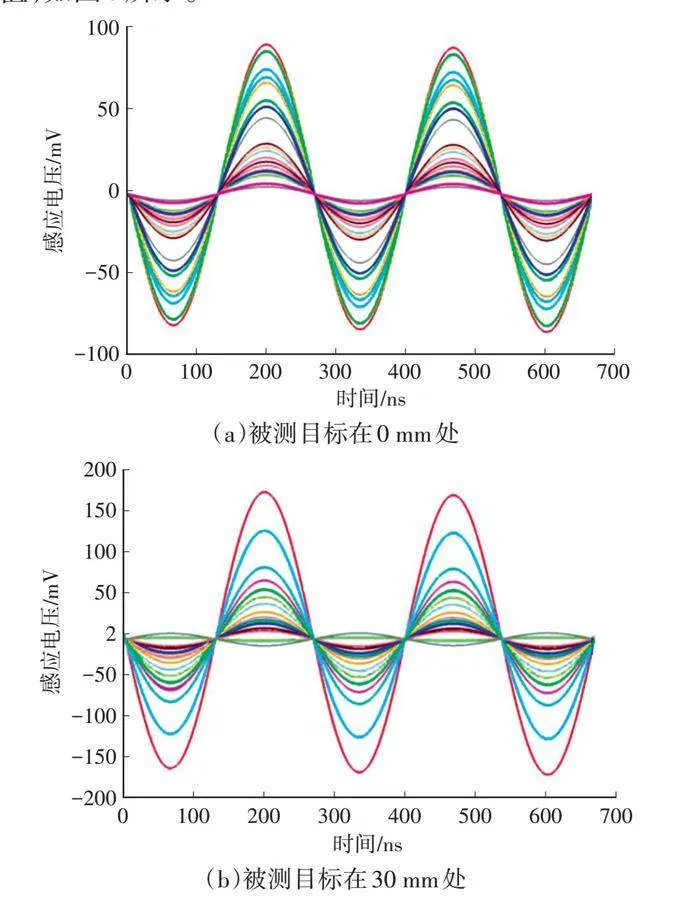
在本文试验设计中，为了充分验证模型的准确性和结构可行性，将电涡流传感器的线圈置于试验平台上，被测目标固定在滑动导轨机构上，在安装时，注意被测目标与传感器的高度测量，通过滑动导轨的左右移动，即代表被测目标在不同位置下的特性，记录在不同位置的感应电压变化。通过与仿真分析的结果进行组合，得到最优结构参数，即：线圈与被测目标间隙为1 mm、激励频率为3.3 MHz进行测试和分析，确定传感器测量装置的参数设置，采集并记录传感器感应电压与位置关系，系统性能验证试验如图8所示。

其中，①为传感器，采用PCB技术制作，②为被测目标，通过被测目标上螺钉调节③间隙的大小，被测目标在④导轨上移动，在PCB上建立坐标，当移动被测目标时，将采集的数据发送给芯片进行数据处理，通过解析的结果与坐标值进行对应，将解析数据和仿真结果对比得到误差。

研制的电涡流位移传感器结构参数为170 mm×40 mm×2 mm，其中线圈由2组正交函数曲线的感应线圈和4匝激励线圈组成，激励线圈电感为6 uH；被测目标选择不锈钢材料，被测目标移动范围为0～90 mm，间隙为1 mm。调节激励电压幅值为5 V，工作频率为3.3 MHz。通过数据处理后得到的试验结果和仿真结果关系如图9所示。

对于被测目标在每个位置r，该误差定义为线性误差εr为：

[εr=Lrmeasured-LridLFS]·100% （13）

式中：[Lrmeasured]为在r位置上的通过解析电路得到的位置，[Lrid]为在r位置上的坐标值，LFS为传感器测量量程。其中仿真结果曲线与实测结果曲线误差如图10所示。

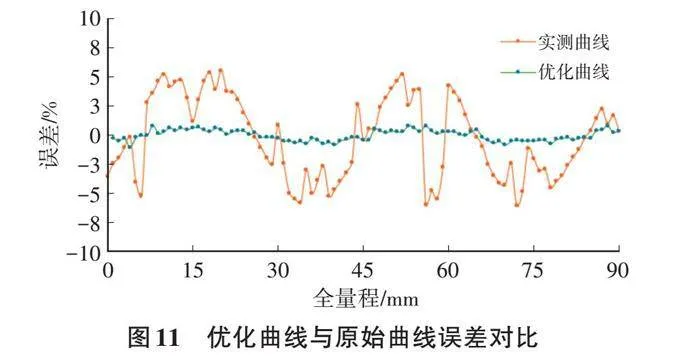
受传感器安装、加工及PCB线圈制造过程的误差影响，由图10可知，全量程原始最大误差为6%，在高精度设备中，误差过大，无法正常使用。通过在仿真软件中微调线圈的走线方式，重新设计线圈的结构参数，补偿线圈由于不对称性引入的误差，并通过动态调节激励频率，改变误差较大位置点的感应幅值。然后与仿真结果进行多点标定，消除固有误差，可以大幅度减小传感器测量误差。利用上面方法对传感器进行优化，优化后的误差最大为1.5%，对比优化前减小了3.5%。其中优化结果与原始实测结果误差如图11所示。

将优化后的参数重新接入相应的检测电路中可以得到性能理想的传感器，大幅减小了研制周期，提高了制造效率。

5 结束语

本文基于Ansys建立了电涡流位移传感器等效模型，根据电磁感应等理论分析不同参数对传感器的影响，验证了涡流位移传感器设计和分析的可行性。其次通过建立试验平台，测量传感器实际位移与仿真数据进行对比分析，得到误差曲线。最后给出多种方法解决受工艺因素影响带来的误差，优化了传感器结构参数，使得精度大幅度提高，大幅减小了研制周期，提高了制造效率，进而说明了基于Ansys有限元法对电涡流位移传感器的设计具有重要的指导意义。

参 考 文 献

[1] NURKOWSKI J， NOWAKOWSKI A. Inductive Sensor for Measuring Linear Displacement and Velocity—Version with Stationary Magnetic Core[J]. Measurement， 2023， 222（10）： 113675.

[2] 彭松. PCB型高精度电磁感应式直线位移传感器研究[D]. 重庆： 重庆理工大学， 2023.

[3] LIM H S， KIM C Y. ISO26262-Compliant Inductive Long-Stroke Linear-Position Sensors as an Alternative to Hall-Based Sensors for Automotive Applications [J]. Sensors， 2022， 23（1）： 245-245.

[4] ALEXANDER R D， GERALDG， SINA F. An Effective Method to Model and Simulate the Behavior of Inductive Angle Encoders[J]. Sensors， 2022， 22（20）： 7804-7804.

[5] ALDI H， MAURO P， GENTJAN Q， et al. Design Optimization of PCB-Based Rotary-InductivePosition Sensors[J]. Sensors， 2022， 22 （13）： 4683-4683.

[6] 李昌， 周松斌. 基于数字锁相放大器的电涡流位移传感器[J]. 电子器件， 2022， 45 （2）： 445-449.

[7] BRUNO B， LORENZO L， GAEL C. Hybrid Magnetic-Inductive Angular Sensor with 360° Range and Stray-Field Immunity[J]. Sensors， 2022， 22 （6）： 2153-2153.

[8] 孙志敬，刘欢，侯文峰.电涡流位移传感器在压缩机中的应用 [J]. 机床与液压， 2021， 49 （19）： 68-71.

[9] FERRAN P， CRISTIAN H， FERRAN M. Position Sensors for Industrial Applications Based on Electromagnetic Encoders[J]. Sensors， 2021， 21 （8）： 2738-2738.

[10] 杨坚， 张善猛， 曾励， 等. 基于ANSYS的电涡流位移传感器仿真分析[J]. 工程机械， 2021， 52 （3）： 40-44+8.

[11] 丁潇凡， 朱学忠. 用于电机位置检测的电涡流传感器电磁场仿真分析[J]. 电测与仪表， 2018， 55 （11）： 94-99.

[12] 姜敏. 电涡流位移传感器仿真方法研究和专用仿真软件开发[D]. 成都： 电子科技大学， 2016.

[13] 徐琳， 王恒， 黄祯， 等. 基于COMSOL有限元法的电涡流传感器仿真[J]. 排灌机械工程学报， 2015， 33 （12）： 1097-1104.

[14] MISRON N， YING Q L， FIRDAUS N R， et al. Effect of Inductive Coil Shape on Sensing Performance of Linear Displacement Sensor Using Thin Inductive Coil and Pattern Guide [J]. Sensors， 2011， 11 （11）： 10522-10533.

[15] 霍守锋， 程树森， 宋小鹏. 平面型线圈阵列电涡流传感器阻抗分析[J]. 冶金自动化， 2011， 35 （3）： 60-64.

（责任编辑 明慧）