螺栓预紧力对风力发电机组变桨轴承强度影响的研究











摘要:变桨轴承是风力发电机组的核心传动部件,为研究螺栓预紧力对其强度的影响,以某型风力发电机组三排滚柱回转支承为研究对象,通过有限元方法建立“轮毂-轴承-叶片”模型,利用梁单元模拟螺栓并施加预紧力,非线性弹簧单元模拟实体滚子,进行变桨轴承静力学仿真计算。对比不同螺栓预紧力下极限工况对三排滚柱回转支承套圈应力、位移、滚动体接触载荷分布规律的影响及螺栓自身强度。结果表明,减小螺栓预紧力时,轴承套圈油槽位置应力减小,滚动体接触载荷减小,套圈位移增大。考虑到轮毂侧的滚动体承载略大于叶片侧,实际装配过程中可适当增大内圈螺栓预紧力。
关键词:滚动轴承;变桨轴承;三排滚柱回转支承;风力发电机组;螺栓预紧力
中图分类号:TH123;TM315 文献标志码:A doi:10.3969/j.issn.1006-0316.2024.10.004
文章编号:1006-0316 (2024) 10-0029-08
Influence of Bolt Preload on Variable Pitch Bearing Strength of Wind Turbine
MENG Gaoqiang,LI Ruijun,LIU Deng,YAN Youzeng
( Wind Energy Institute, Mingyang Smart Energy Group Limited, Zhongshan 528400, China )
Abstract:Variable pitch bearing is the core transmission component of wind turbine. In order to study the influence of bolt preload on its strength, a three-row roller slewing support of a wind turbine was taken as the research object, and a "hub-bearing-blade" model was established by finite element method. The beam element was used to simulate the bolt, the preload force was applied, and the nonlinear spring element was used to simulate the solid roller. The static simulation of variable pitch bearing is carried out. The distribution law of stress and displacement, contact load of rolling element and bolt strength of three-row roller slewing bearing ring under different bolt preloading conditions were compared. The results show that the stress in the oil groove of bearing ring decreases, the contact load of rolling body decreases, and the displacement of ring increases. Considering that the bearing capacity of the roller on the hub side is slightly larger than that on the blade side, the pre-tightening force of the inner ring bolt can be appropriately increased during the actual assembly process.
Key words:rolling bearing;variable pitch bearing;three-row roller slewing bearing;wind turbine;bolt preload
变桨轴承是风电机组的核心传动部件之一,安装在风电机组叶片与轮毂之间,作用是通过调整风力发电机叶片的迎风角度来控制风轮的转速及风机的输出功率,从而确保风机在各种风速条件下都能高效、稳定地运行,提高风能利用率。变桨轴承的性能直接影响风机的使用寿命,如果其可靠性不好,容易导致风机因故障而停机或频繁更换零部件,从而增加安全风险和维护成本。因此,为确保变桨轴承的可靠性,国内外学者开展了相关研究。黄艺龙等[1]通过采用壳单元模拟滚子-滚道接触面的方法有效减少了大型三排滚柱式转盘轴承有限元计算分析的计算量。王存珠等[2]利用有限元方法研究不同螺栓预紧力对四点角接触球轴承载荷分布的影响,结果表明预紧力越大接触载荷分布越均匀。杨成奇[3]研究变桨轴承套圈载荷特性时考虑了刚性耦合区域对结构刚性的影响。Kania[4]采用正确载荷变形特性的桁架单元对滚动体与滚道的接触模型进行等效处理,分析了柔性套圈条件对滚动体接触载荷及滚道接触区域变形情况的影响。Daidié[5]采用非线性弹簧和实体耦合的方式模拟滚动体与套圈滚道间的接触,其中弹簧非线性刚度由Hertz接触理论确定。陈红涛[6]对变桨轴承进行了参数化设计,分析设计中参数变化对载荷及接触应力分布的影响,建立螺栓连接的有限元模型,研究了螺栓应力与预紧载荷之间的关系等。
目前对四点角接触球变桨轴承的研究较全面,但其尺寸大、沟道结构复杂,加工及装配难度大。随着风电机组不断扩容,要求变桨轴承具备更大的承载能力,大兆瓦机组大都采用三排滚柱变桨轴承,而相关研究相对较少。
三排滚柱回转支承径向滚动体及轴向滚动体能够承受较大的径向力、轴向力和倾覆力矩,其相较于四点角接触球轴承具有工作载荷高、运行速度低、重量轻等优点,但结构尺寸大、承载高、套圈易变形,刚性套圈假设具有局限性[7]。大型回转轴承运行工况复杂、测试困难且成本较高,故本文在球轴承研究的基础上,通过有限元方法研究不同螺栓预紧力下三排滚柱回转支承的承载能力、滚动体载荷分布规律及螺栓自身强度,为风力发电机组变桨轴承强度评估提供参考。
1 建立有限元模型
1.1 轴承模型
以某机型风力发电机组三排滚柱回转支承为例,其结构如图1所示,由双排轴向圆柱滚子及单排径向圆柱滚子、内圈、外圈、密封圈组成。轴向圆柱滚子承受轴向力和倾覆力矩,径向滚子承受径向载荷[1]。
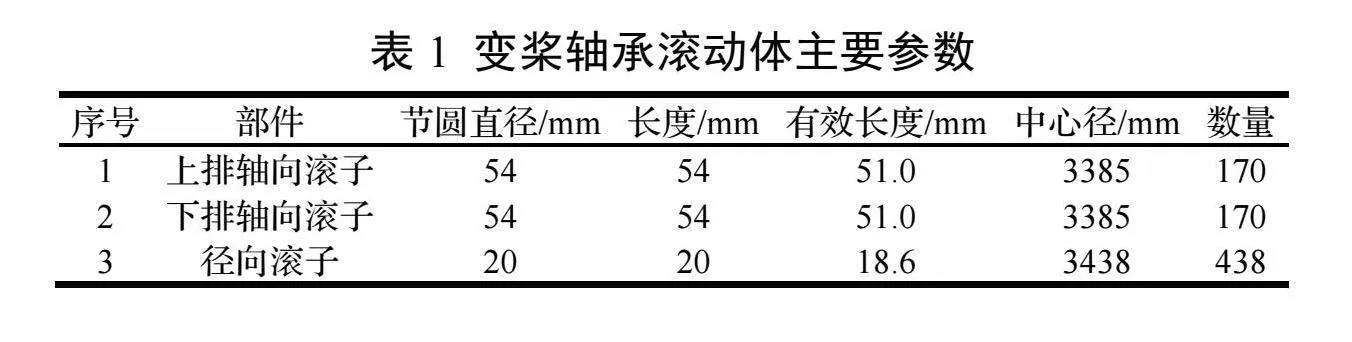
三排滚柱回转支承主要参数如表1所示。
变桨轴承在风电机组中的装配结构如图2所示,轴承外圈通过106个M42(双头螺柱)高强度螺栓[8]沿环向均布与轮毂相连,取拧紧系数为1.3,预紧力为694~902 kN;内圈通过128个M39(双头螺柱)高强度螺栓沿环向均布与叶片相连,取拧紧系数为1.2,预紧力为393.3~472 kN。
1.2 有限元模型
轴承整体有限元模型如图3所示。
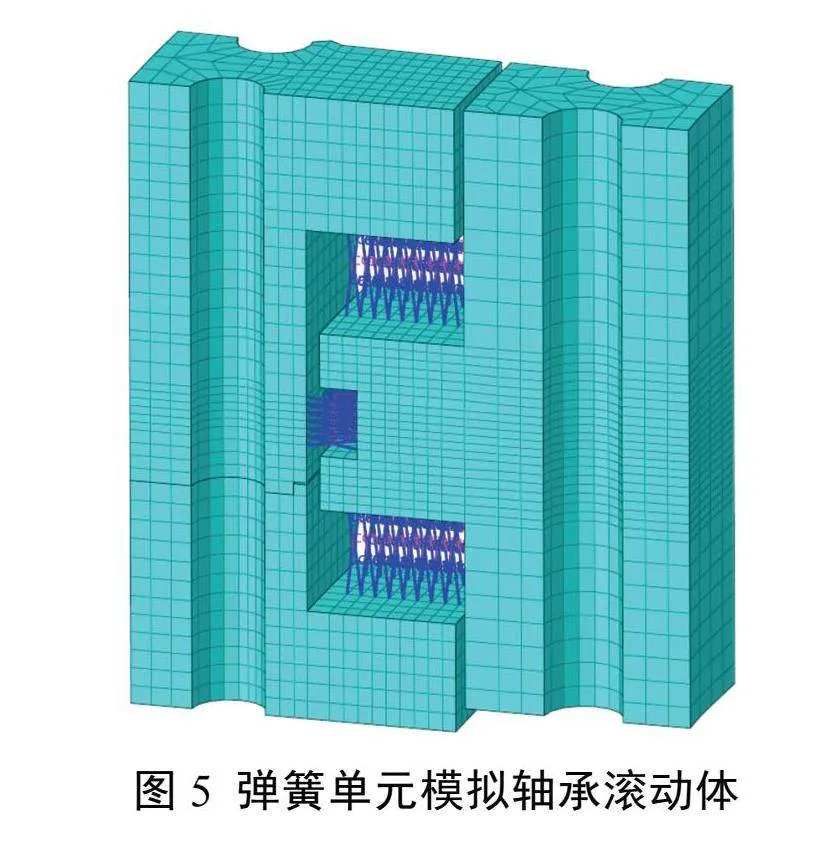
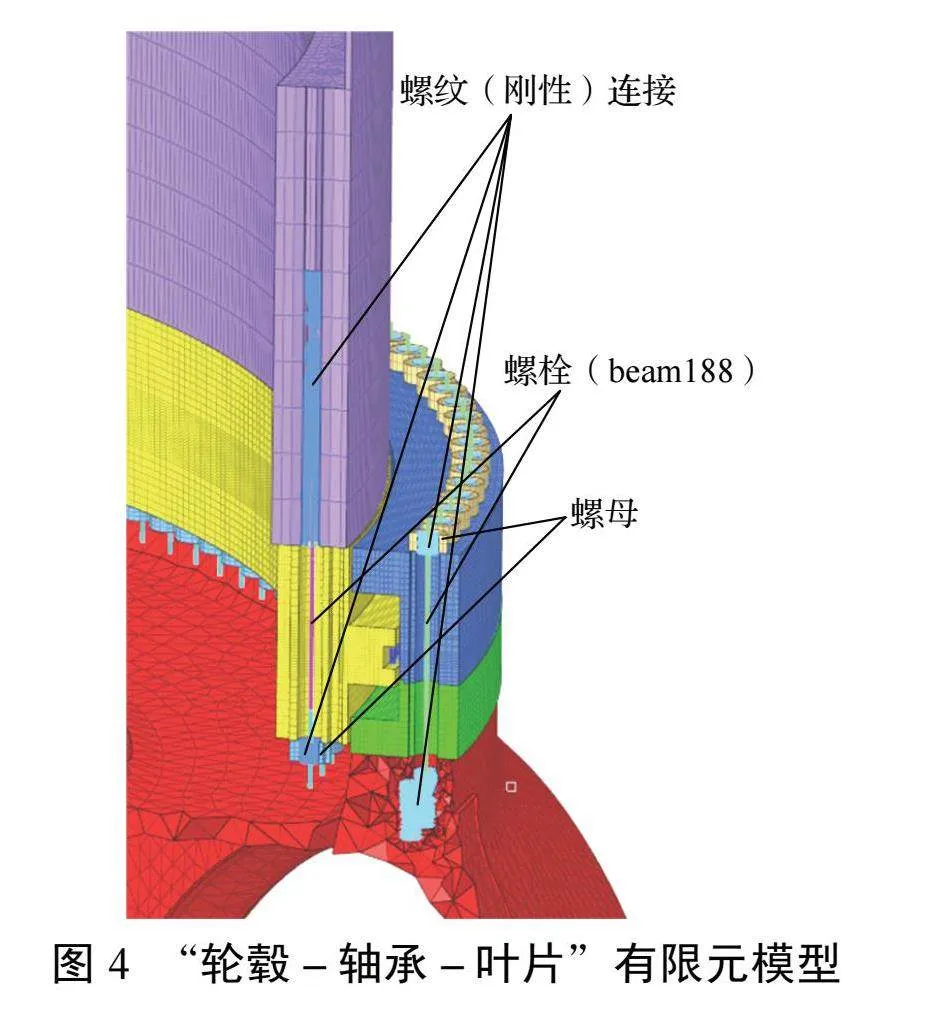
变桨轴承支撑刚度影响其承载能力,因此需要建立包含螺栓连接的“轮毂-轴承-叶片”整体有限元模型[9],如图4所示。变桨轴承套圈为关键部件,为保证求解精度,采用solid185单元低阶六面体结构化网格划分。由于风电机组上安装的三排滚柱回转支承结构尺寸大、滚柱数量多,非线性接触对数量庞大,受载后的接触状态在计算过程中不断更新迭代,为避免非线性接触计算引起的不收敛问题,采用非线性弹簧combin39单元[10]替代圆柱滚子的接触变形行为,再通过刚性连接将弹簧单元与轴承内外圈进行连接,如图5所示。采用梁单元beam188模拟变桨轴承内圈与叶片、外圈与轮毂连接的螺栓[11],并添加prets179单元施加预紧载荷[12],如图6所示,减少建立实体单元建模产生的计算量,进一步提高计算效率。
有限元建模中,滚子-滚道承受载荷时的接触区域和弹簧单元的力学性能通过载荷-变形关系确定。计算为:
(1)
(2)
(3)
式中: 为切片刚度; 为滚动体切片载荷; 为滚动体切片的变形; 为弹性常数; 为滚动体切片数量;k=1,2,3,分别表示径向、轴向下排、轴向上排滚动体;i为第i个滚动体;j为滚动体第j个切片; 为滚动体有效长度。
根据式(2)生成轴向滚子和径向滚子的载荷-变形曲线,其中变形量为负表示弹簧单元仅受压不受拉,用来模拟滚子实际受载状态。
为提高算精度,每个轴承滚子用多个弹簧进行模拟。轴向滚动体切片数为9,等效弹簧个数为9;径向滚动体切片数为7,等效弹簧个数为7个。利用式(1)~(3)得到滚动体载荷与变形关系如图7所示。
遵循经典Hertz接触原理[3],滚子-滚道接触区域近似为椭圆,为方便建模,将模拟接触区域简化成尺寸为 ×2b的矩形,计算为[1]:
(4)
(5)
式中: 为最大的接触载荷; 为等效弹性模型; 为滚子和滚道曲率半径之和; 、 分别为滚道和滚子的弹性模量; 、 分别为滚道和滚子的泊松比。
根据NREL公式[1]计算上下排滚子的最大接触载荷为:
(6)
(7)
式中: 和 分别为上排和下排滚子的最大接触载荷; 和 分别为上排和下排滚道的中心直径; 和 分别为上排和下排滚子的数量; 和M分别为滚子所受的轴向力和倾覆力矩。
计算得,上排和下排滚子的接触尺寸 ×2b均为51 mm×0.734 mm,最大接触载荷均为256 873 N。
1.3 材料及接触设置
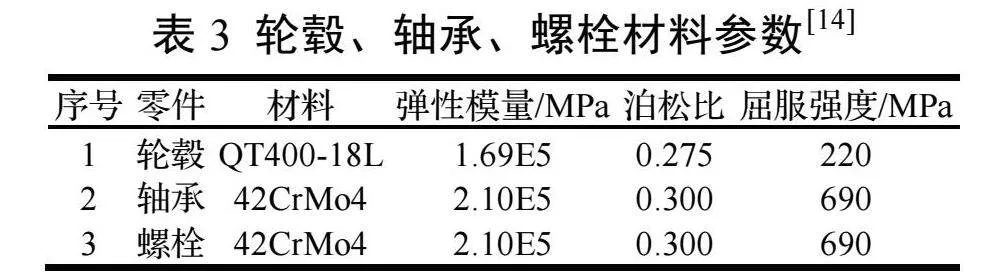
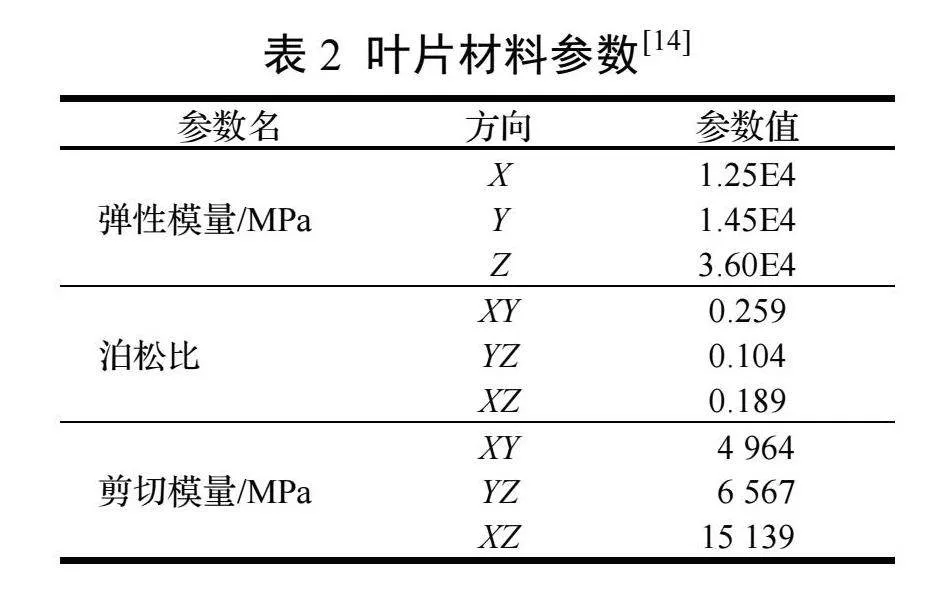
叶片材料性质为正交各向异性,其他部分均为各向同性,材料参数如表2、表3所示。
针对变桨轴承工作时各接触面间的情况,设置模型之间的相互作用关系。各零部件之间均为摩擦接触,在接触位置设置对应的摩擦系数[15],如表4所示[14]。
1.4 边界条件及载荷
风电机组轮毂与主轴配合,主轴安装于轴承座,轴承座安装于机座,机座通过塔筒与地面相连,故轮毂与主轴配合面设置为全约束,限制端面节点的全部自由度。
如图8所示,以叶根几何中心为原点建立局部坐标系,X轴指向轴承零位,Z轴沿轴线方向。在坐标原点建立一个质量单元MASS21,用reb3(柔性连接)将质量单元与叶片端面所有节点耦合,实现极限工况加载。
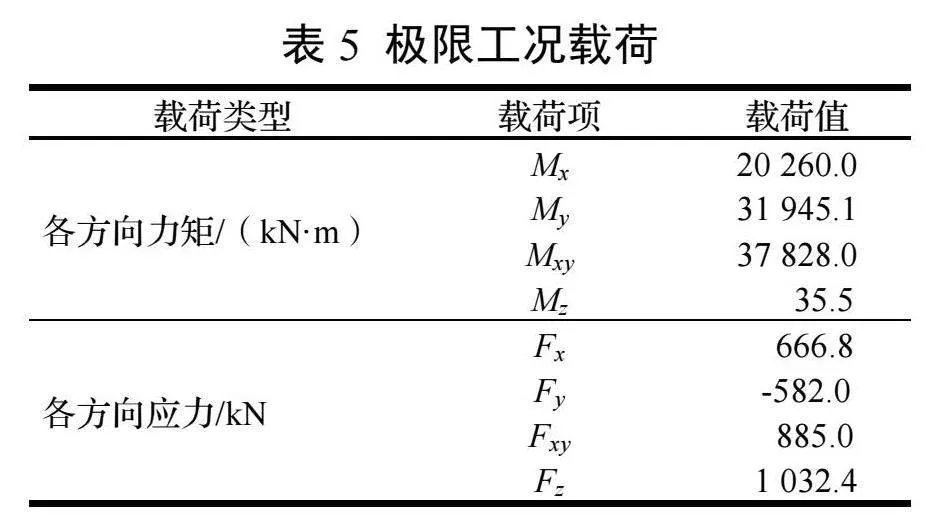
静强度研究极限工况下轴承套圈的载荷值如表5所示。可以看出,载荷Mz相对非常小,故不考虑轴承旋转,约束加载点Z方向的旋转自由度。
分别计算内外圈预紧力组合时的极限工况的静强度,螺栓预紧力范围和预紧力工况分别如表6、表7所示。
2 强度分析
强度分析研究内容包括:极限载荷作用下轴承套圈应力是否满足材料屈服强度;不同预紧工况对轴承套圈应力的影响;不同预紧工况对螺栓自身强度的影响;不同预紧工况作用下轴承滚动体接触载荷的变化。
2.1 套圈应力
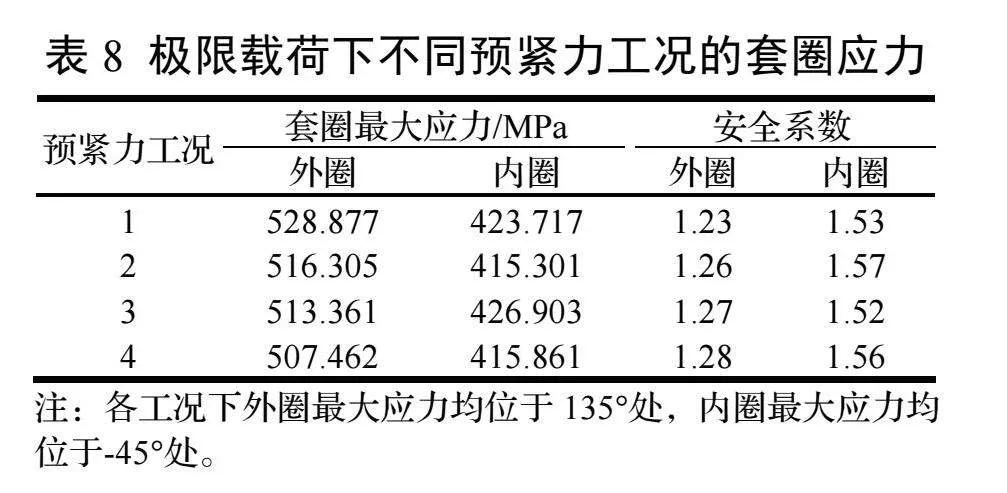
极限载荷作用下,不同螺栓预紧力工况计算的轴承套圈应力如表8所示。可以看出,预紧力工况1变桨轴承套圈应力较高,其外圈最大等效应力为528.877 MPa,位于135°叶片侧油槽处;内圈最大等效应力为423.717 MPa,位于-45°轮毂侧油槽处。强度均满足要求。轴承
套圈最大应力出现在外圈油槽位置,与轴承实际磨损位置相符。
2.2 套圈位移
极限载荷作用下,不同螺栓预紧力轴承套圈的位移如表9所示。可以看出,当螺栓预紧力增大时,内、外轴向位移减小,环向位移增大,此时表明螺栓预紧力增大,提高了结构的整体刚度。
2.3 螺栓应力
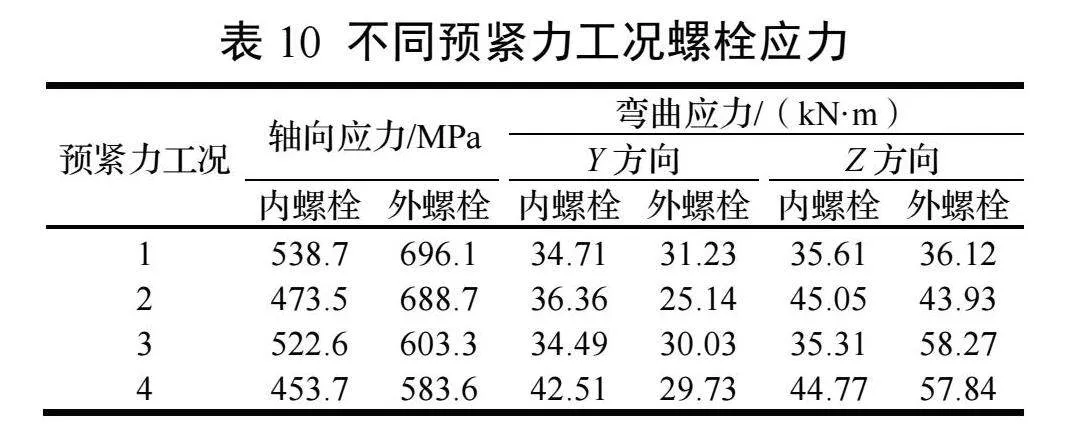
极限载荷作用下,不同预紧力工况的螺栓轴向应力、Y和Z方向(beam单元坐标)弯曲应力如表10所示。可以看出,当预紧力增大时,螺栓轴向应力增大,Y和Z方向弯曲应力减小。
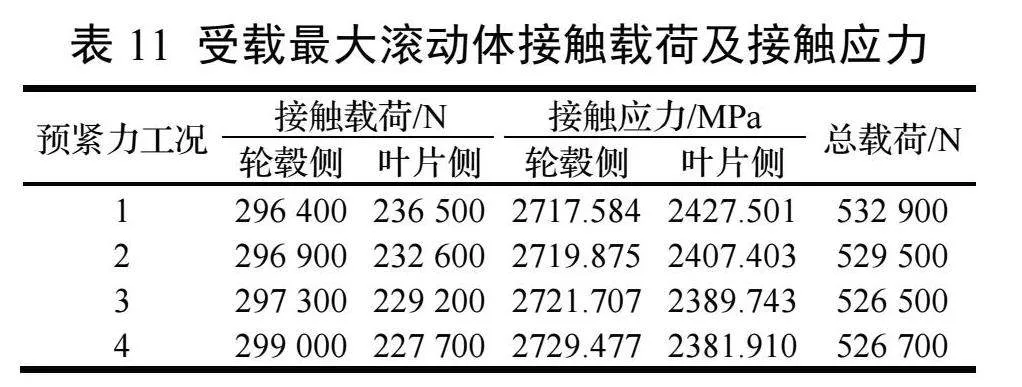
2.4 滚动体接触载荷及接触应力
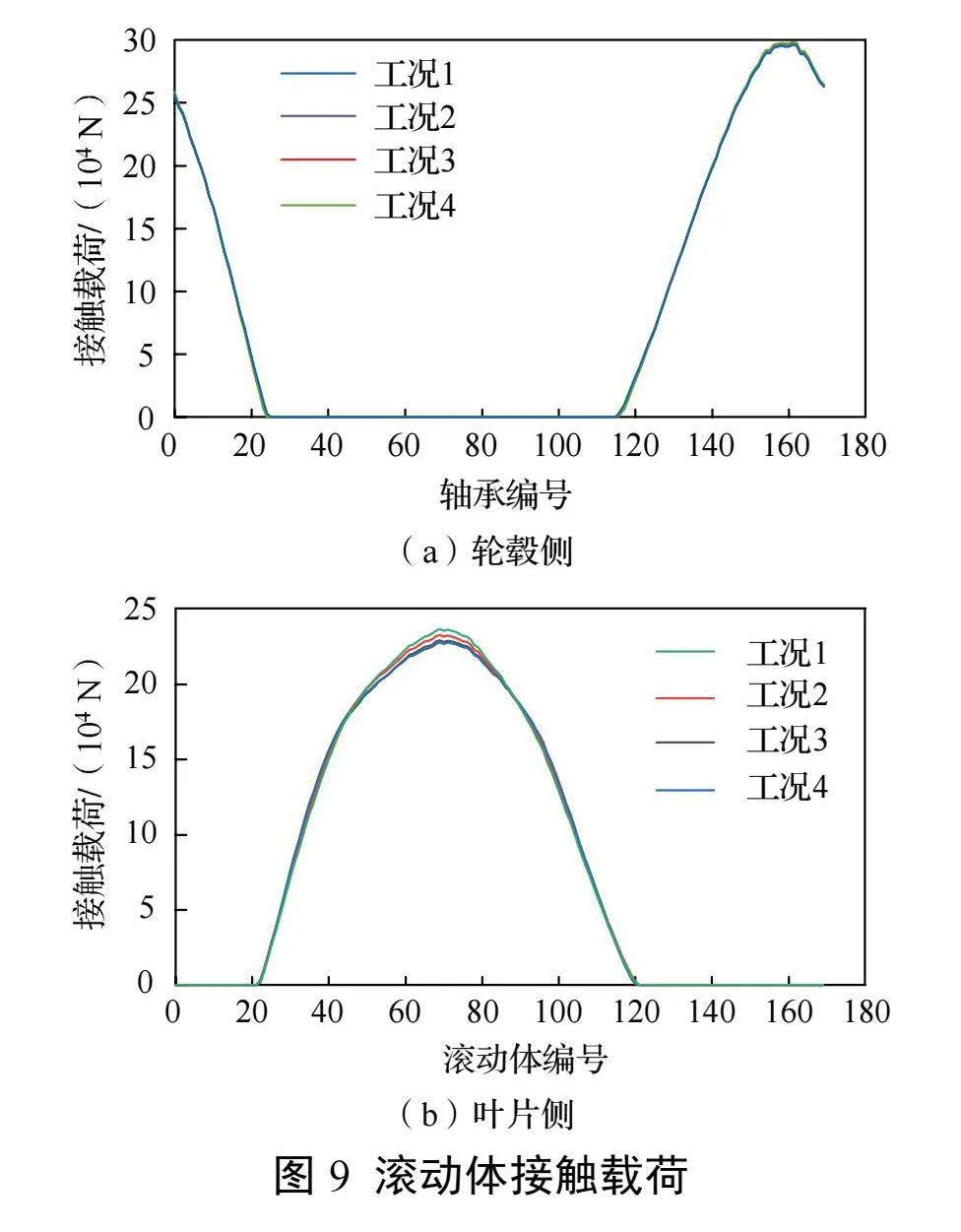
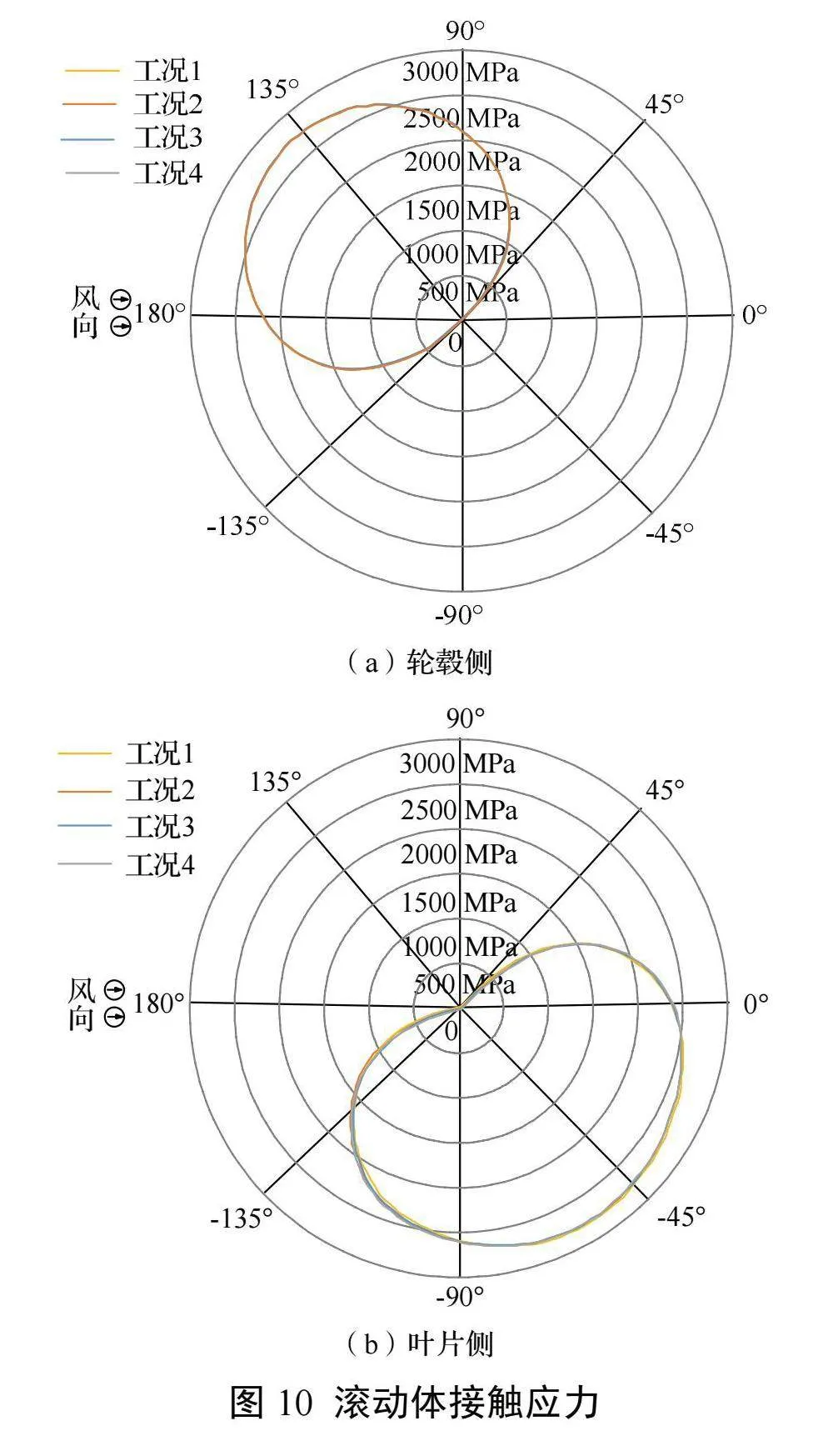
受载最大滚动体接触载荷及接触应力如表11、图9、图10所示,其中,不同预紧力工况下,轮毂侧受载最大滚动体均为162号滚子(滚子编号从变桨轴承坐标系0°位置起始),近叶片侧均为70号滚子。可以看出,螺栓预紧力的大小并未影响工作载荷时轴承的整体受力情况,仅影响滚动体载荷的数值。由于滚道内外圈参数相同,所以接触应力相同。相较理论计算,轮毂侧滚动体受载较大,叶片侧较小。
由有限元计算结果及相关理论分析可得:
(1)对比表9、表10,在内圈螺栓预紧力不变的情况下,随着外圈螺栓预紧力的增加,轴承外圈油槽的应力增大,轴向位移减小,环向位移增大;相反,内圈油槽的应力减小,轴向位移增大,环向位移减小。表明外圈螺栓预紧力使外圈结构刚性增强,由于油槽位于外圈结构尺寸突变位置,存在应力集中现象,因此随着外圈刚性增大,应力集中更明显。同时,内圈结构刚度相对变小,在同一载荷作用下,内圈结构变形增大,故内圈的轴向位移增大,环向位移减小。
(2)对比表9、表10外圈螺栓预紧力不变时,增大内圈螺栓预紧力,轴承内外套圈油槽位置应力增大,轴向位移增大,环向位移减小,有助于叶片载荷的传递。
(3)由表11可知,当内圈、外圈预紧力增大时,螺栓受载增大,轴向应力增大,结构刚度提高,受载后螺栓自身的弯曲应力减小。
(4)由表12可知,当螺栓预紧力减小时,轮毂侧滚动体受载增大,接触应力增大;叶片侧滚动体受载减小,接触应力减小。螺栓预紧力减小时,“轮毂-轴承-叶片”结构整体刚度减小,轴承承受更大的载荷。
(5)对比理论计算(表2)与有限元滚动体接触载荷(表12),结果基本一致。考虑结构变形轮毂侧滚动体载荷略大于叶片侧,由表12知,当螺栓预紧力增大时,轴承滚动体与套圈的初始过盈量增大,故滚动体受载增大。
3 结论
三排滚柱变桨轴承利用有限元方法进行计算的结果与NREL理论计算结果基本一致,验证了有限元模型的准确性。有限元方法相较于理论计算考虑了套圈变形。对比不同预紧工况可知,螺栓预紧力增大可提高结构刚度、减小受载后的变形,但增大螺栓预紧力使滚动体与套圈初始过盈量增大,滚动体受载增大;由受载情况可知,轮毂侧的滚动体受载略大于叶片侧,减小外圈螺栓预紧力或增大内圈预紧力可提高轴向滚动体受载的均匀性;增加螺栓预紧力时,螺栓应力增大、强度减弱。故在满足强度要求的前提下,应适当减少外圈螺栓预紧力,增大内圈螺栓预紧力。
参考文献:
[1]黄龙艺,傅航,王钰. 大型三排滚柱式转盘轴承的有限元计算分析[J]. 机械强度,2022,44(3):627-634.
[2]王存珠,陈观慈,李肖杰. 螺栓及其预紧力对大型转盘轴承接触载荷分布的影响[J]. 轴承,2016,33(1):24-27.
[3]杨成奇. 变桨轴承套圈载荷特性及疲劳寿命研究[D]. 大连:大连理工大学,2018:20-23.
[4]LUDWIK KANIA. Modeling of rollers in calculation of slewing bearing with the use of finite elements[J]. Mechanism and Machine Theory,2006(41):1359-1376.
[5]ALAIN DAIDIÉ,ZOUHAIR CHAIB,ANTOINE GHOSN. 3D Simplified Finite Elements Analysis of Load and Contact Angle in a Slewing Ball Bearings [J]. Journal of Mechanical Design,2008(26):1-8.
[6]陈红涛. 兆瓦级风力发电机组变桨轴承有限元分析[D]. 洛阳:河南科技大学,2012.
[7]张红伟,陈曙光,薛六涛,等. 大型变桨轴承的力学性能研究现状及展望[J]. 轴承,2017(7):59-62.
[8]中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会. 六角头螺栓:GB/T 5782-2016[S]. 北京:中国标准出版社,2016.
[9]ALAIN DAIDIÉ1,ZOUHAIR CHAIB,ZOUHAIR CHAIB. 3D Simplified Finite Elements Analysis of Load and Contact Angle in a Slewing Ball Bearing[J]. Journal of Mechanical Design,2008,130(8):082601-1-8.
[10]XIAO Bin,LI Biao,XIA Chunyan. Power flow method used to vibration transmission for two-stage vibration isolation system[J]. Jixie Gongcheng Xuebao,2011,47(5):106-113.
[11]HE Peiyu,WANG Yun. Effect of high-strength bolts and supporting structures on the carrying capacity of three-row roller slewing bearings[J]. Journal of mechanical engineering science,2021,235(11):2053-2064.
[12]陈晨,刘勇,李亚,等. 风力发电机变桨轴承强度分析及影响因素[J]. 轴承,2023(6):59-63.
[13]GAO XH,HUANG XD,WANG H. Effect of raceway geometry parameters on the carrying capability and the service life of a four-point-contact slewing bearing[J]. Journal of Mechanical Science and Technology,2010,24(10):2083-2089.
[14]国家市场监督管理总局,国家标准化管理委员会. 球墨铸铁件:GB/T 1348-2019[S]. 北京:中国标准出版社,2019.
[15]王委,陈捷,洪荣晶,等. 摩擦因数对单排球转盘轴承接触次表层的影响[J]. 轴承,2018,44(9):44-48.

