依托含参幂函数 基本类型妙应用

含参数的幂函数的应用问题，是幂函数最为重要的一个基本应用类型。如何快速切入并正确解决幂函数应用中的含参数问题，关键在于把握幂函数的基本概念、图像特征和基本性质。

一、活用概念

幂函数的概念是解决幂函数应用问题的一个基本切入点，特别是幂函数应用中的含参数问题，结合系数、常数项、指数、底数等几个不同要素，对标其概念，能够给问题的切入与应用创造条件。

点评：解决含参数的幂函数的应用问题，要从函数解析式的系数、常数项、指数、底数等几个不同要素进行分析与判断。

二、数形结合

幂函数的图像是解决幂函数应用问题的一个基本思维点。正确掌握幂函数的图像特征与基本性质，为进一步综合应用奠定基础。在实际解题时，要从“数”的抽象视角切入，合理利用“形”的直观形象解题，真正达到数形结合与巧妙应用。

例2 （多选题）现有4个幂函数的部分图像，如图1所示，则下列选项可能成立的是（ ）。

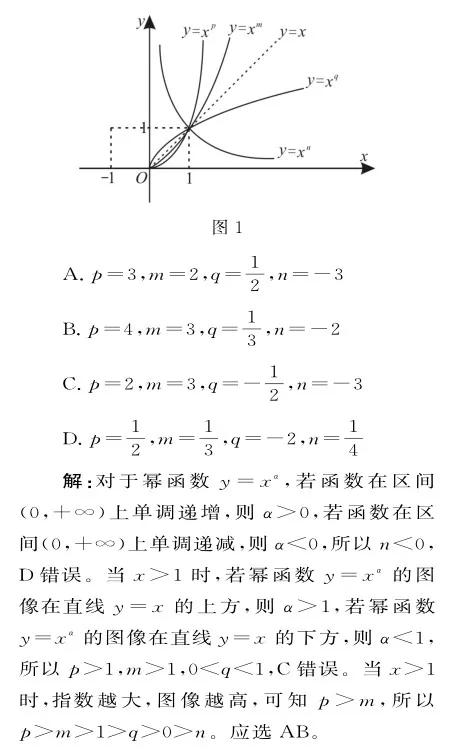
点评：解答本题的关键是利用幂函数的图像，挖掘隐含条件并利用分类讨论进行分析与验证。

三、分类讨论