依托分段函数场景 归纳基本题型应用

涉及分段函数的应用问题，一直是高考考查的热点与难点问题之一，也是高考试题中的一类常见题型。此类问题以分段函数为问题场景，借助相关知识加以合理交汇融合，常考常新，形式多样，变化多端。

由①②③可知，若f（ a）=3成立，则实数a= 1或a= 2。

点评：解决分段函数中的含参数问题的四个基本步骤：对参数的取值范围进行分类讨论；把参数代入到相应的不同解析式中；通过解方程来确定参数的值；检验所求的值是否在所讨论的范围内。

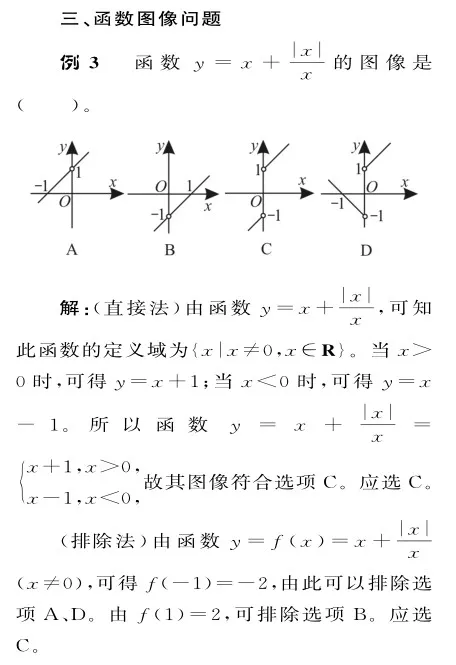
点评：判断分段函数图像的关键是结合各段上具体的函数解析式来确定相应的图像，也可以借助一些特殊点所对应的函数值，结合选项中函数的图像，借助排除法来判断。

四、与方程融合问题

例4 试讨论方程x2- 4 | x |+5-m=0的实根的个数。

解：由x2- 4 | x |+5-m=0，可得x2-4 | x | + 5 =m。

点评：求解分段函数与不等式的交汇问题，关键是利用分段函数的解析式，结合不等式的应用，使得分段函数与不等式的交汇问题顺利解决。

六、实际应用问题

例6 一列货运火车从某站出发，匀加速行驶一段时间后开始匀速行驶，过了一段时间，火车到达下一站停车，装完货以后，火车又匀加速行驶，一段时间后再次匀速行驶。下列图像可以近似地刻画出这列火车的速度变化情况的是（ ）。