面向振动信号分析方法的电力变压器故障检测分析

摘 要：针对变压器的故障诊断及定位方法，探讨了面向振动分析法的变压器故障诊断技术。该技术涉及铁心和绕组振动的原理，以及机械结构变化对频率集中度和振动稳定性的影响。通过互信息方法，实现了故障位置的精准定位。实验表明，振动分析法不仅能提供与传统方法相当或更优的检测精度，还具有非侵入式和实时的监测优势，是电力系统维护和故障预防的重要手段。

关键词：振动分析法 变压器 故障检测 振动测试系统

中图分类号：TM413

Analysis of Fault Detection of Power Transformer Based on Vibration Signal Analysis Method

LI Zhichao GE Hao ZHAO Xinyi XIANG Zimo SHI Yiying

State Grid Beijing Tongzhou Power Supply Company， Beijing City， 101100 China

Abstract： According to the fault diagnosis and positioning method of transformer， the transformer fault diagnosis technology based on Vibration Analysis method is discussed. The technique involves the principle of core and winding vibration， and the influence of mechanical structural changes on frequency concentration and vibration stability. Through the mutual information method， the precise positioning of the fault position has been achieved. The experiment shows that the Vibration Analysis method can not only provide a comparable or better detection accuracy than the traditional method， but also has the advantages of non-invasive and real-time monitoring， which is an important means of power system maintenance and fault prevention.

Key Words： Vibration Analysis method; Transformer; Fault detection; Vibration testing system

变压器在电力系统中至关重要，但长期运行易发生故障。传统故障检测需断电，影响供电且可能造成二次伤害。因此，发展无须断电的在线监测技术尤为必要。本研究通过分析变压器在正常运行与故障状态下的振动信号特征，探讨了基于振动分析法的变压器故障诊断技术，实现了对变压器潜在故障的早期预警及精准定位。

1 变压器振动的原理

铁心振动的主要成因在于硅钢片展现的磁致伸缩特性。若将电源电压为 ，单位为伏特（V），则可以推导出，铁心振动的加速度为：

式（1）中：为硅钢片沿轴向的尺寸，单位为mm；为硅钢片磁致伸缩率，单位为H/m；为磁场中的磁感应强度，单位为T；为硅钢片的横截面积，单位为mm2；为电源电压幅值，单位为V；-为铁心对应的绕组匝数，以匝数为单位。由此可知，铁心振动加速度与电源电压的关系成正比，即。

但考虑铁芯在实际运行中会受到磁滞效应和涡流效应的双重影响，导致磁致伸缩特性与磁感应强度之间呈现出一种复杂的非线性关系。因此，在表征振动信号时，可将100Hz作为基准频率，并适当引入少量整数倍的高频分量[1]。

2 变压器振动频率集中度与机械结构稳定性

正常工作的变压器振动信号稳定，但机械结构变动会导致其变化。振动分析法通过分析信号差异评估变压器状态。本研究采用实时信号分析与历史数据比对双维度方法。变压器振动源于铁心和绕组，基频为100 Hz，含高频成分，主要分布于1 000 Hz以下。本文分析此频段内振动分量。在典型条件下，基频成分占主导，高频成分较少，成分比例稳定，据此定义频率集中度指标。

式（2）中：表示频率为的振动谐波的幅值，单位为m/s²。

振动频率分量的比重可通过DFC来量化，特别是针对100 Hz成分的显著性。DFC计算实时，分析瞬时振动数据，不依赖长期历史记录。变压器机械稳态时，振动信号集中在100 Hz，DFC值趋近1。高频成分增多时，频率分布散乱，DFC值下降。实时监控DFC值可评估变压器工作状态。

3 变压器故障定位

根据变压器振动原理，本文利用互信息方法构建了一种框架，将变压器振动信号特征参数与影响变压器运行状态的因素联系起来，实现精准定位故障位置。互信息描述了一个变量在另一个变量已知时不确定性降低的程度，即两个变量间共享的信息量。互信息值越高，变量间相关性越强[3]。随机变量的不确定性可通过熵度量：

式（3）中，是随机变量取特定值的概率，已知随机变量，那么随机变量的条件熵为：

则随机变量和的互信息为：

绕组振动与电流平方直接相关，电流增大时，绕组振动增强。铁心振动与电压平方正相关，电压增加导致铁心振动加剧。变压器中，绕组振动、铁心振动及总振动间有关系。铁心异常时，振动。模式变化，整体振动水平调整[4]。为识别振动变化原因及定位故障，可采用互信息分析法计算电流、电压变化量与总振动变化量的互信息，判断原因并定位故障，定义故障关联度指标[4]：

式（6）中：为振动影响因素，包括电压和电流的变动；为振动信号特征参数变化量；FCD是振动影响因子与特征参数相关度的量化指标，用于评估相关性，其增加表示故障可能性增大。基于振动分析的变压器诊断方法优于传统技术，可实现在线实时监控和准确故障定位，但存在传感器安装和信号特征提取的难点。传感器布置需考虑设备结构和故障特征，缺乏统一标准。振动信号复杂，缺乏完备故障特征数据库，难以实现精确对应。

5 变压器故障检测实验

针对前述分析，本文提出基于振动信号分析的电力变压器故障检测方法。该方法通过振动信号特征分析，提出频率集中度和振动稳定性指标进行状态监测，并结合互信息方法实现故障诊断与定位。为验证本文方法的使用价值，本文与传统变压器绕组检测方法进行了对比。具体实验过程及结果如下。

5.1 故障概况

某变压器于2022年9月投入运行，额定容量240 MVA，额定电压1 100/ kV，额定频率50 Hz。2023年检修时采用传统检测技术未能判断原因，故采用本文设计的基于振动分析法的故障监测与诊断分析方法。

5.2 实验过程

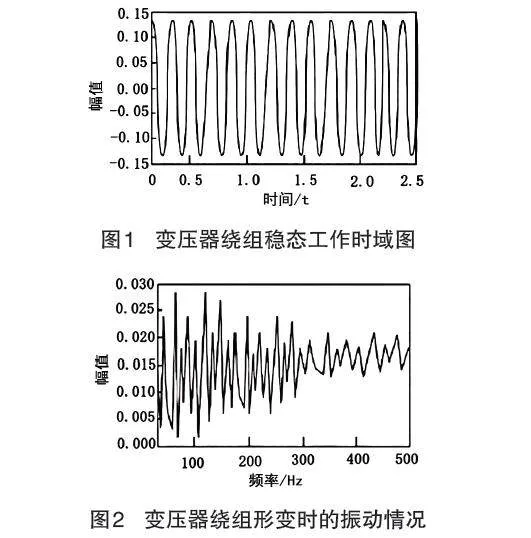
在实验开始前，需对变压器进行信号采集。鉴于实验室目前不具备直接获取变压器绕组信号的条件，对绕组形变引起的故障信号采集较为困难。本次研究引入了变压器绕组的等值电路参数（、、、、、、、），并利用这些参数进行变压器绕组状态的综合诊断分析。常规条件下，变压器绕组未变形的状态为饼状，一旦形变发生，各线圈将表现出不同程度和特征的形变。变压器绕组稳态工作时域波形如图1所示，波动范围在-0.15到+0.15之间，时间跨度为0～2.5 s，运行正常。但持续运行10 min后，如图2所示，出现不同频率振动。工作频率在0～100 Hz时，振动幅值为0.000～0.030；100～300 Hz时，振动幅值为0.005～0.025；300～500 Hz时，振动幅值为0.010～0.020。数据表明，0～300 Hz内振动幅值较高，可能存在严重运行问题，须检测维修。

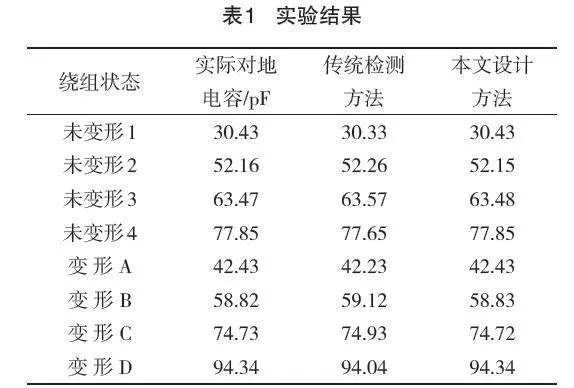
5.3 实验结果

依据上述实验条件，本文选定两种不同状态的变压器绕组：一为未变形状态，标记为未变形1-4；另一为变形状态，标记为变形A-D。考虑到变压器型号的差异，每种型号对应不同的绕组配置。本研究在确保各变压器对地电容相等的前提下，对比了传统绕组检测方法和本研究提出的基于振动分析的绕组检测方法在测量变压器对地电容方面的效果。相关的实验数据和分析结果详见表1。

从表2的实验结果来看，本文设计的基于振动分析的故障检测方法与传统方法相比，具有更高的一致性和精确度。对于未变形绕组，本文方法与实际对地电容值接近，误差极小，表明振动分析法能准确反映变压器绕组状态。对于变形绕组（变形A至D），本文方法同样匹配度高，误差范围小，证明该技术能准确诊断绕组异常变形。相较于传统方法，本文设计的振动分析在变形绕组检测中更为精确，可能因其更敏感于绕组变形引起的微小变化。

6 结语

通过振动信号的分析和实验验证，本研究展示了基于振动分析法的变压器故障诊断技术在准确性方面的优势。该技术能够在不中断变压器服务的情况下，有效地监测其运行状态，并及时识别出潜在的故障。与传统方法相比，本文提出的技术在不仅可以提供与传统方法相当或更优的检测精度，还能通过其非侵入式和实时的监测优势，成为电力系统维护和故障预防中的重要手段。

参考文献

[1] 赵若希.750kV高压并联电抗器的振动测试与故障分析[J].中国新技术新产品，2023（20）：58-60.

[2] 杨凯东.变压器绕组的振动信号检测方法分析[J].电子技术，2023，52（5）：304-306.

[3] 吴欣烨.面向振动信号多特征值的电力变压器故障检测方法分析[J].中国高新科技，2023（15）：85-87.

[4] 陈月，许秀英，梁春英，等.变压器故障诊断及分析方法[J].农机使用与维修，2023（8）：124-128.

[5] 李楠，马宏忠，崔佳嘉，等.电力变压器绕组振动声纹特性分析[J].应用声学，2022，41（5）：785-793.