理论运行速度与公路线形设计及评价方法研究

摘要 为保证公路运营期间的行车安全，该文研究了直线长度、平曲线半径、纵坡坡度等线形参数对运行速度的影响，明确了平直、平曲线、纵坡、弯坡组合路段划分原则和理论运行速度预测模型。最后，以某二级公路为研究对象，利用同一路段运行速度V85和设计速度V差值的绝对值ΔV来评价其线形安全，研究成果可供类似项目提供借鉴。

关键词 运行速度；影响因素；分段评价；预测模型；评价结果

中图分类号 U412 文献标识码 A 文章编号 2096-8949（2024）19-0031-03

0 引言

近年来，公路工程建设规模越来越大，安全性要求也越来越高，目前公路线形安全性评价大多是基于理论运行速度V85，即在气候、路况等外部条件比较理想的条件下，车辆第85%分位的行驶速度，其可能大于设计速度，也可能小于设计速度。然而很多设计人员在确定路线线形时重视指标的选择，而不重视安全性评价，容易引发交通安全事故，甚至造成一定的人员伤亡，因此进一步研究理论运行速度及线形评价方法具有重要的意义。

1 公路运行速度影响因素

从公路线形角度来看，影响运行速度的因素主要有直线长度、平曲线半径、纵坡坡度及弯坡组合等，具体阐述如下：

（1）直线的影响。

直线具有距离短、方向明确等优势，是公路设计时最常用的线形之一，直线过长或过短都会影响车辆的运行速度。德国学者经过多年研究，发现驾驶员在直线上连续行驶超过3 min时，内心会感觉单调、出现疲劳感，从而不自觉地超速行驶，而当直线长度过短时，驾驶员需频繁制动，降低车辆运行速度，以保证行车安全。

（2）平曲线半径的影响。

一般情况下，平曲线半径越大，车辆运行速度越快，但是平曲线半径对不同车型运行速度的影响程度不同。比如小客车的自重较轻，动力性能好，运行速度受平曲线半径影响大；而大货车的自重大，动力性能相对较差，运行速度受平曲线半径影响小。

（3）纵坡的影响。

纵坡对车辆运行速度的影响较大，且上坡段和下坡段的影响机理不同。在上坡路段，车辆会受到驱动力及空气、路面、惯性等产生的阻力，车辆运行可视作加速度大小固定的匀减速运动，力学方程可用式（1）表达[1]：

T=Rw+Rr+Rl （1）

式中：T——驱动力（kN）；Rw——空气阻力（kN）；Rr——路面阻力（kN）；Rl——惯性阻力（kN）。

在下坡路段，车辆在自身重力作用下，重力势能转化为动能，车辆运行速度会增加，且运行速度增加至一定值后会趋于稳定。比如小客车下坡滑行会稳定115 km/h左右，大货车下坡滑行会稳定在60～80 km/h。

（4）弯坡组合的影响

在部分山区路段，只能利用“平曲线+纵坡”的方案通过，车辆行驶时会同时受到曲线和纵坡的影响。如果在下坡时遇到曲线，尤其是小半径曲线，驾驶员会认为这是高危路段，会降低车辆运行时速；如果前方遇到上坡，且平曲线半径较大，车辆运行速度降低不明显。

2 公路线形评价流程及要点分析

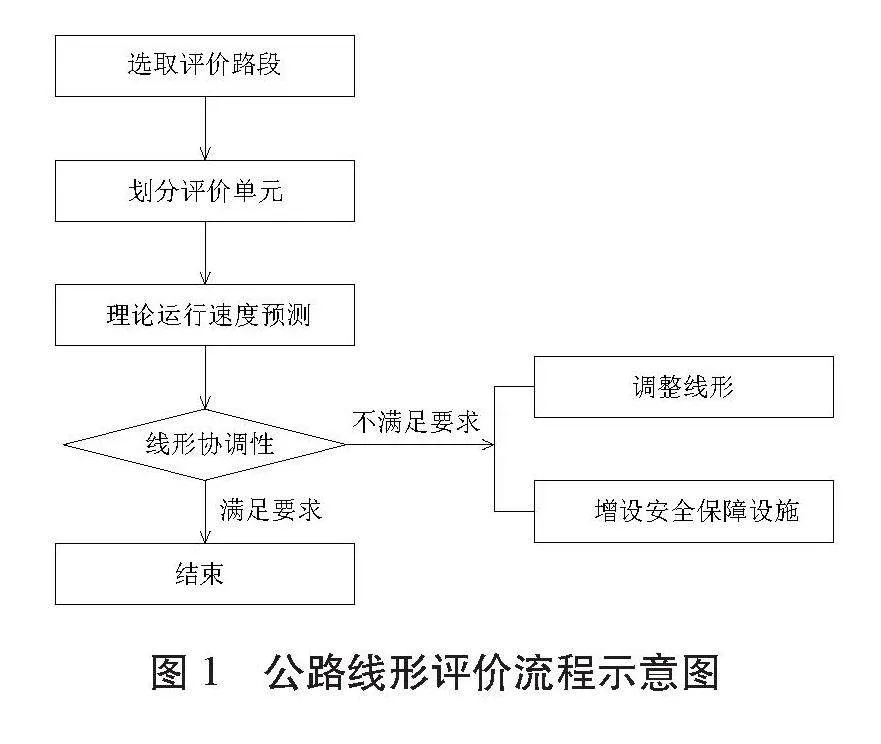
2.1 公路线形评价流程

公路线形是采用“分段评价”思想，即路线方案初步设计完成后，要先将待评价路段划分为若干个评价单元，对其运行速度进行预测，再根据《公路项目安全性评价规范》（JTG B05—2015）对运行速度协调性进行评价，具体评价流程如图1所示：

2.2 公路线形评价单元划分

由《公路项目安全性评价规范》（JTG B05—2015）可知，公路线形评价单位可依据圆曲线半径和纵坡，以低等级公路为例（二级公路、三级公路），具体划分原则如表1所示[2]：

此外，隧道路段是指驶入隧道洞口前200 m至驶出隧道洞口后100 m，互通立交的主线路段为减速车道的渐变段起点至加速车道渐变段终点。

2.3 理论运行速度预测

（1）预测步骤。

公路各个线形评价单元运行速度的预测步骤如下：首先，确定第1个线形评价单元起点的初始运行速度（一般取设计速度），并根据评价单元类型选择相应的运行速度预测模型，预测第1个线形评价单元终点的运行速度；其次，以第1个线形评价单元终点作为第2个线形评价单元的起点，利用运行速度预测模型预测第2个线形评价单元终点的运行速度；最后，不断重复上述步骤，直至预测出最后一个分析单元终点的运行速度。

（2）平直路段运行速度预测。

对于短平直路段，可认为其起点和终点的运行速度不变，对于平直路段，需综合考虑路段长度、车辆加速度、车辆期望速度等进行预测，见式（2）和式（3）[3]：

（2）

a=amin+（amax−amin）（1−vin ve ） （3）

式中：vout、vin——平直路段起点速度和终点速度（km/h）；a、amax、amin——分别为车辆加速度、最大加速度、最小加速度（m/s2）；ve——期望速度（km/h）。

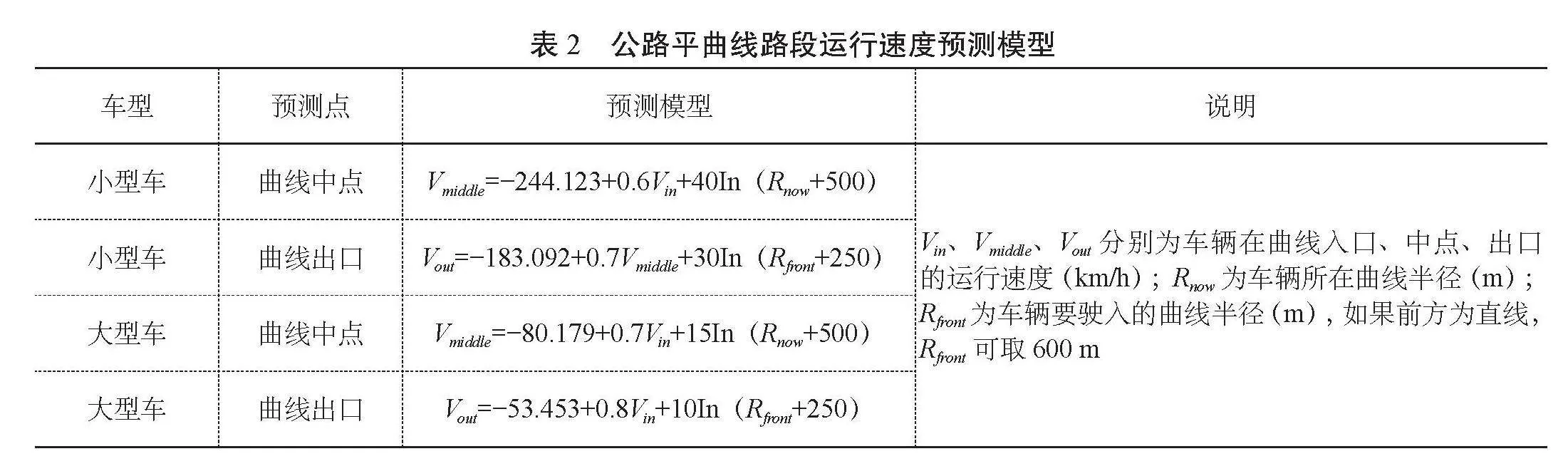
（3）平曲线路段运行速度预测。

由于车辆在平曲线路段的行驶轨迹是不断变化的，其运行速度预测时应从曲线中点分段，及分别预测曲线中点和曲线出口的运行速度，具体预测模型如表2所示：

（4）纵坡路段运行速度预测。

结合相关研究成果，车辆在上坡和下坡路段的运行速度应根据纵坡坡度进行折算[4]。

比如上坡路段，当纵坡坡度在3%～4%，小客车和大货车的运行速度应每1 000 m分别降低5 km/h、10 km/h直至最低运行速度；当纵坡坡度＞4%，小客车和大货车的运行速度应每1 000 m分别降低8 km/h、20 km/h直至最低运行速度。

比如下坡路段，当纵坡坡度在3%～4%，小客车和大货车的运行速度应每500 m分别增加10 km/h、7.5 km/h直至期望速度；当纵坡坡度>4%，小客车和大货车的运行速度应每500 m分别增加20 km/h、15 km/h直至期望速度。

（5）弯坡路段运行速度预测。

在弯坡组合路段，车辆运行速度同时受圆曲线、纵坡的影响，因此在预测运行速度时不仅要从曲线中点分段，还要区分上坡、下坡，具体预测模型如表3所示：

3 公路线形评价实例分析

（1）工程概况。

该文研究对象为省道公路，其路线全长32.6 km，起点和终点均与地方道路相接，总体走向为南北向，起讫桩号为K0+000～K32+600，设计洪水频率为1/50，设计等级为二级公路，双向两车道，设计速度为40 km/h，横断面宽度为8.5 m（0.75 m土路肩+3.5 m行车道+3.5 m行车道+0.75 m土路肩），横坡为2%。目前，路线初步设计方案基本确定，最小直线长度为200 m、最小圆曲线半径为220 m、最小纵坡为0.6%、最大纵坡为5.2%、最小坡长为150 m，为保证路线线形设计质量，拟基于上述运行速度预测方法评价路线协调性。

（2）线形评价标准。

该文利用同一路段运行速度V85和设计速度V差值的绝对值ΔV=|V85−V|来分析线形协调性。当ΔV<20 km/h，说明线形协调性好；当ΔV≥20 km/h，说明线形协调性不良[5]。

（3）线形评价结果。

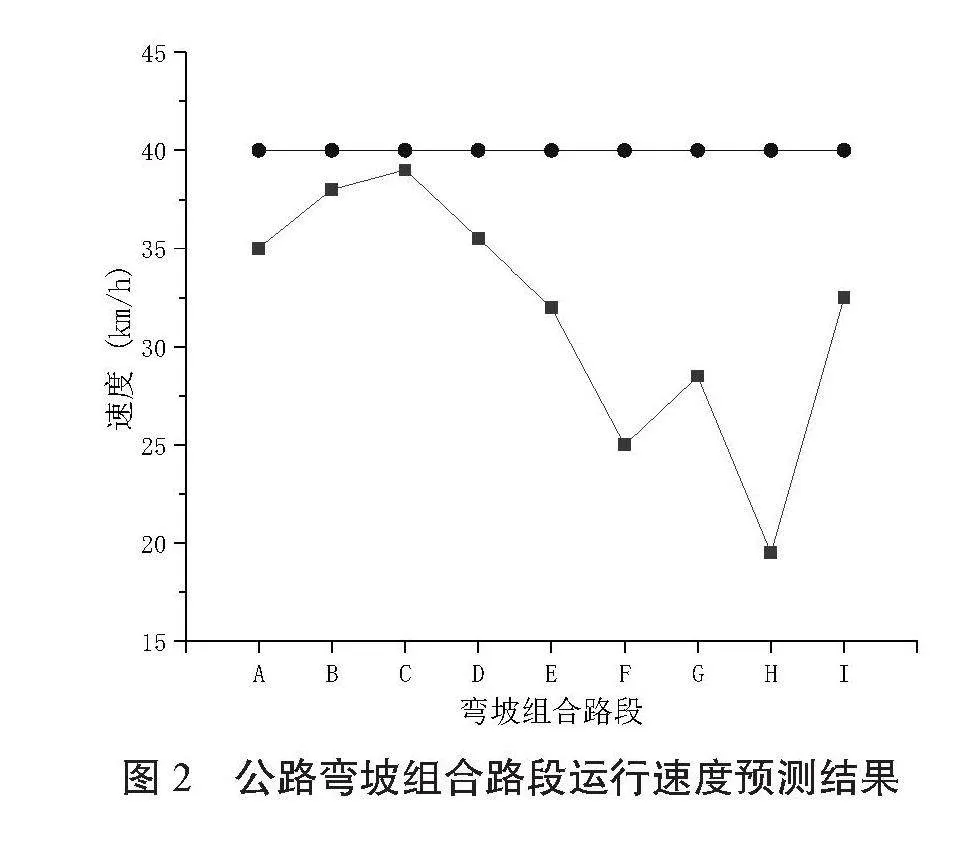
基于2.2节的原则，将该公路划分了40个评价单元，运行速度预测的数据量大，受限于篇幅，该文只针对危险性较大的弯坡路段开展分析。该公路沿线共有9处弯坡组合路段，分别编号为A～I，不同路段的运行速度预测结果如图2所示：

弯坡组合路段的运行速度均小于设计速度。经计算，得到A～I路段的ΔV分别为5.0 km/h、2.0 km/h、1.0 km/h、4.5 km/h、8.0 km/h、15.0 km/h、11.5 km/h、20.5 km/h、7.5 km/h。由此可知：除H路段外，其他路段的ΔV均小于20 km/h，则线形协调性好的路段占比为88.9%。对于线形协调性不良的路段，应调整线形，如布线条件受限，可增加安全保障设施，比如限速标志、危险标识、视线诱导设施等。

4 结论

该文主要分析了公路理论运行速度的影响因素、预测模型，并以某二级公路为研究对象开展案例分析，得到了以下几个结论：

（1）公路运行速度是V85可能大于或小于设计速度，受直线长度、圆曲线半径、纵坡等线形参数的影响较大。

（2）公路线形评价前，要先按圆曲线半径和纵坡将其划分为若干个平直、平曲线、纵坡、弯坡组合路段，并根据相应的预测模型来预测各个路段起点和终点的运行速度。

（3）公路线形协调性可用ΔV=|V85−V|评价，尽可能将ΔV控制在20 km/h内，否则应调整线形或增加安全保障设施。

参考文献

[1]伍华勇，贺阳.运行速度及其在公路路线设计中的应用分析[J].交通世界，2023（19）：79-82.

[2]王路.道路线形设计指标选用及安全评价研究[D].南京：东南大学，2017.

[3]李鑫磊.基于车辆行驶仿真的道路线形安全评价研究[D].济南：山东建筑大学，2016.

[4]龙立敦，符锌砂，秦涛.基于理论运行速度的公路设计线形安全性实时评价系统设计[J].中外公路，2015（5）：329-333.

[5]赵金凤.山区高速公路线形使用质量综合评价研究[D].广州：华南理工大学，2012.

收稿日期：2024-04-15

作者简介：王磊刚（1991—），男，本科，工程师，从事公路勘察设计工作。