基于PSO-BP模型的差速器装配密封质量预测

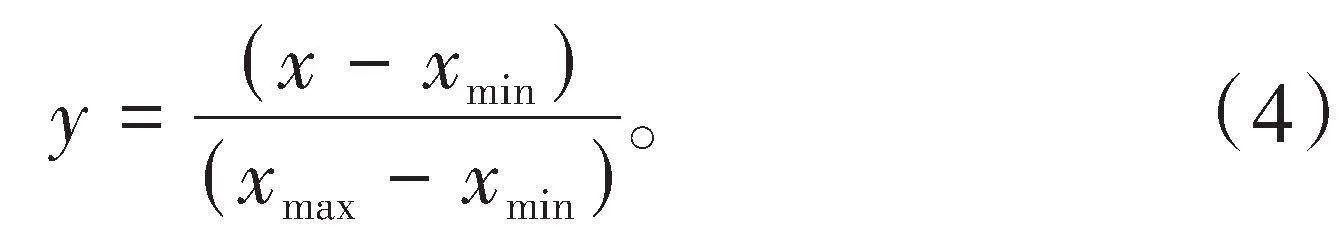
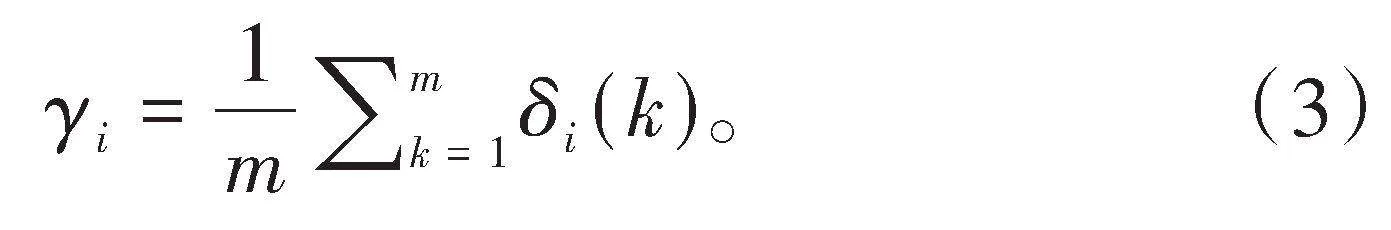
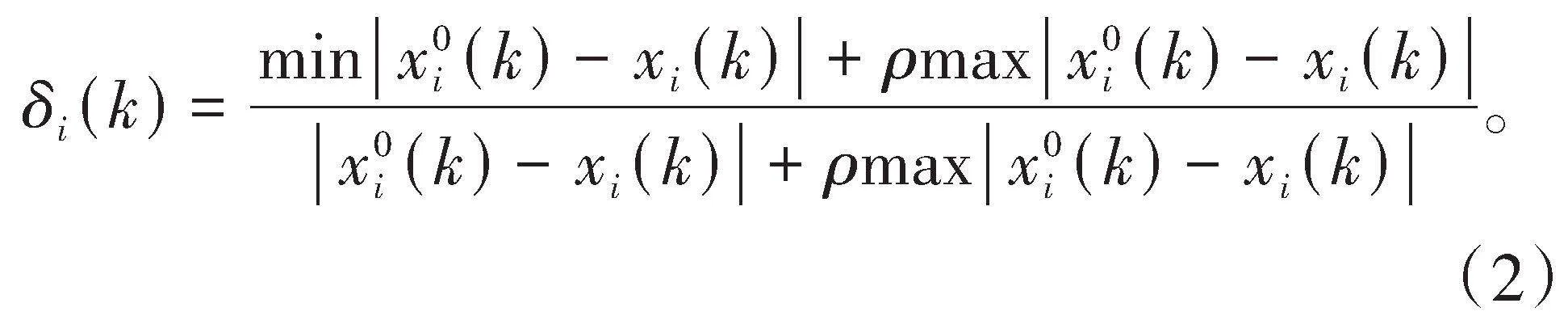
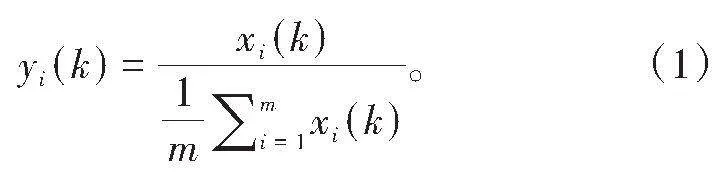
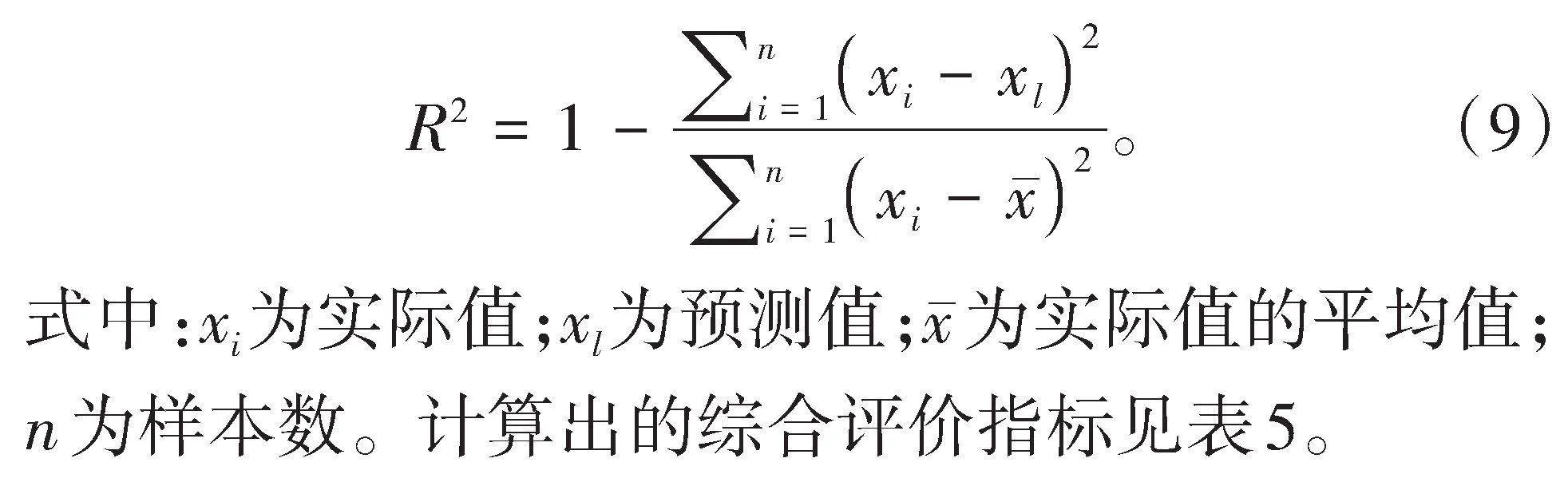
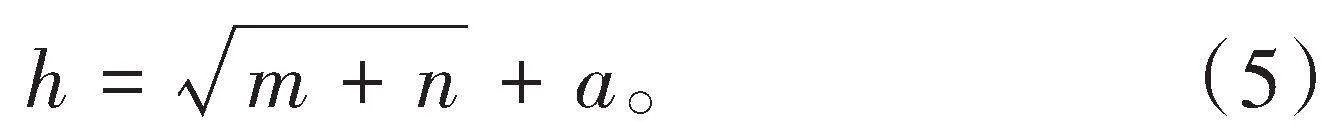
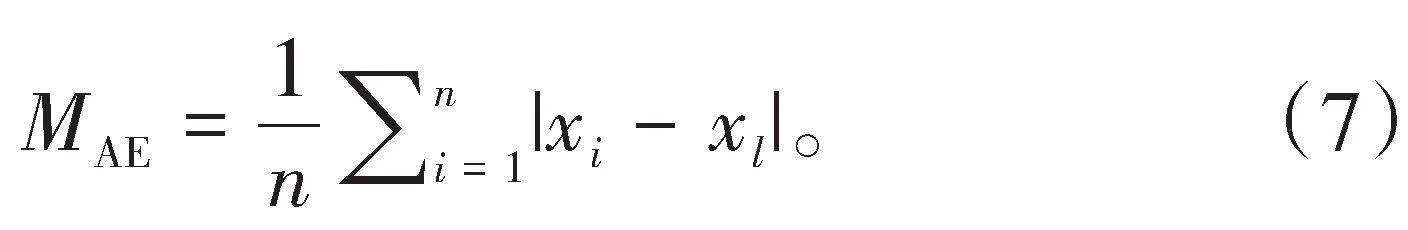
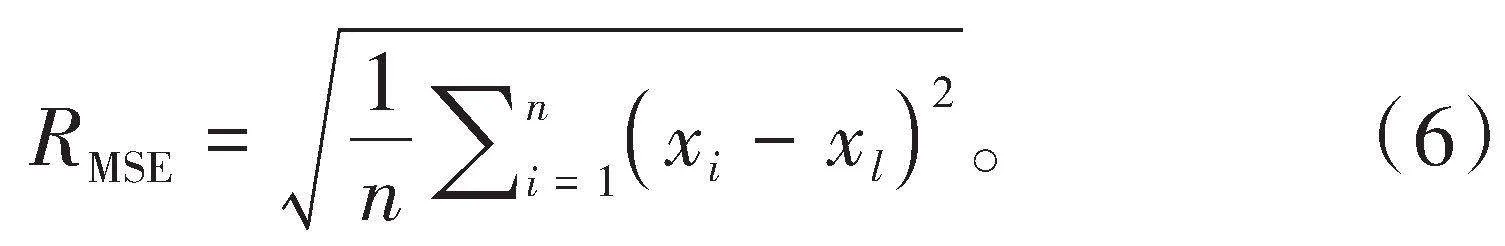
摘 要：为了对林业运材车差速器总成装配密封质量进行事前预测，提高其产品质量及装配合格率，提出一种灰色关联分析算法结合粒子群（PSO）优化BP神经网络的预测模型。将由灰色关联分析算法筛选出影响差速器总成密封质量的关键装配工艺参数作为输入变量，差速器总成泄漏值作为输出变量，创建基于粒子群（PSO）算法优化BP神经网络（PSO-BP）的预测模型，结果表明，由灰色关联分析简化后的PSO-BP预测方法得到的平均相对误差最小为1.18%。在此基础上，应用PyQt5 GUI库开发差速器总成泄漏值预测系统。研究结果可以为差速器总成密封质量预测提供理论依据。

关键词：运材车辆； 差速器； 密封质量； 灰色关联分析算法； 粒子群优化算法； 反向传播神经网络

中图分类号：TH161+.7 文献标识码：A DOI：10.7525/j.issn.1006-8023.2024.05.014

Research on Sealing Quality Prediction of Differential Assembly Based on PSO-BP model

Abstract： In order to predict the sealing quality of the differential assembly of forestry timber tranpsort vehicle trucks beforehand and improve the quality of its products and the assembly qualification rate， a prediction model based on grey correlation analysis algorithm combined with particle swarm （PSO） optimized BP neural network is proposed. The key assembly process parameters affecting the sealing quality of differential assembly screened out by the grey correlation analysis algorithm are taken as input variables， and the leakage value of differential assembly is taken as output variable to create a prediction model based on particle swarm algorithm optimized BP neural network， and the results show that the PSO-BP prediction method simplified by the grey correlation analysis obtains the smallest average relative error of 1.18%. On this basis， PyQt5 GUI library is applied to develop a differential assembly leakage value prediction system. The results of the study can provide a theoretical basis for the prediction of differential assembly sealing quality.

Keywords： Timber transport vehicle； differential； sealing quality； grey correlation algorithm； particle swarm optimization （PSO）； back propagation neural network （BP）

0 引言

林业生产对于维持生态平衡，提供可持续的木材资源以及促进社会经济发展具有至关重要的作用。林业运材车是林业生产的关键部分，其担负着全球90%以上短距离木材运输的重任［1］。这些车辆的差速器需要具有高耐用性以适应复杂地形和重负载，保证转弯时轮胎的内外转速不同，避免打滑和转向问题［2］。差速器的密封质量直接影响转弯安全性和传递效率，因此，通过预测其密封质量来采取控制措施，是提升作业工具性能和安全性的关键。

针对装配质量的预测方法，国内外学者已经进行了大量研究，方群霞等［3］使用粒子群优化算法结合反向传播神经网络模型，建立了一个预测模型来分析注塑工艺参数，结果表明，该模型能有效缩短模具生产周期。Wei等［4］通过开发粒子群（PSO）和BP神经网络（PSO-BP）模型解决中国东北冬季输油问题，结果表明，该模型在精度上优于传统BP模型，可以有效预测管道压降。方喜峰等［5］提出了一种基于粒子群和支持向量机（PSO-SVM）的模型，旨在提高船用柴油机装配质量的预测精度以及缩短预测时间。孟冠军等［6］应用量子粒子群优化算法与支持向量回归（QPSO-SVR）模型于生产过程，实现对装配质量的预测和事前控制。Hu等［7］提出了一种改进的PSO-BP混合预测模型以准确预测矩形管顶隧道比表沉降，证明该模型在学习能力和稳定性上表现优越，适用于广泛的沉降预测研究。陈资等［8］通过结合遗传算法和支持向量机（GA-SVM）来预测数控机床装配质量，与传统方法相比，证明了该模型的高实用价值。董海等［9］利用装配工艺状态空间模型进行废旧机床再制造质量预测，案例研究显示该方法显著提高了预测精度。Shen等［10］提出了一种基于PSO-BP算法，用于识别光纤复合材料结构的载荷位置，结果证明该方法比传统模型更准确，对复合材料健康监测具有重要应用价值。

上述研究为本研究提出的林业运材车差速器密封质量预测模型奠定了理论基础。本研究以灰色关联分析算法筛选出的关键装配工艺参数作为输入变量，泄漏值作为输出变量，建立基于BP神经网络的差速器密封质量预测模型，并利用粒子群算法的全局搜索能力对其进行优化以提高预测速度和精度；将训练完成的预测模型作为差速器密封质量预测系统的基础模型，实现对差速器密封质量的高效预测以及可视化展示。

1 因素分析及数据处理

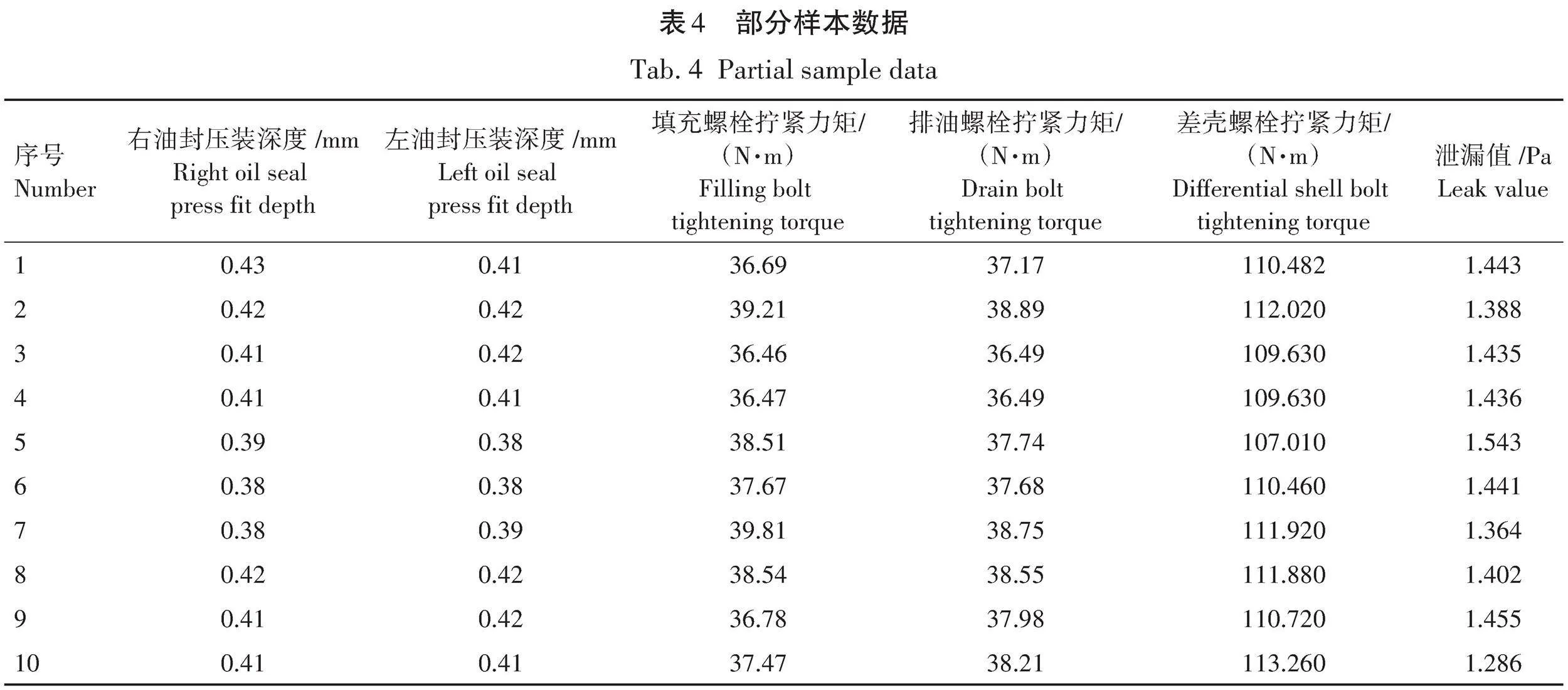
通过分析差速器的装配工艺，确定影响差速器总成密封质量的因素有零部件清洁度（总成杂质重量）、行星齿轮齿隙、油封压装深度以及其他部件的螺栓拧紧力矩等因素。泄漏值常被用来衡量差速器总成密封质量是否合格。分析差速器装配工艺可得到11个影响差速器总成密封质量，即影响总成泄漏值（X0）的装配工艺参数，见表1。通过对哈尔滨市某公司差速器装配线实地调研，对其装配工艺进行分析，得到这11种装配工艺参数对其密封质量有直接影响。

为了节省模型的预测时间以及提高模型预测精度，本研究使用灰色关联分析算法有效地排除一些灰色关联度较小的装配工艺参数，利用灰色关联度较大的装配工艺参数训练神经网络以达到简化BP神经网络模型的目的。

1）首先收集差速器生产线上的初始装配数据，通过哈尔滨市某公司的制造执行系统（MES）进行收集，见表2。

Note： The numbers 1 to 10 in the first column of the table represent the number of each data set.

2）无量纲化处理样本数据

为了排除由于上述11个装配工艺参数间的量纲不同以及数值数量级间的差异，有必要对其进行无量纲化，避免直接使用灰色关联分析算法分析原始数据导致的大数据序列覆盖小数据序列［11］。本研究利用均值法将原始数据进行无量纲处理，其中均值法（）见式（1）

式中：xi为样本初始数据，其中i=1，…，n；k=1，…， m。

3）计算各装配工艺参数的灰色关联系数

根据式（2）计算各装配工艺参数的灰色关联系数（）

式中：xi0为参考序列，即差速器总成泄漏值的均值化结果；xi为比较序列，即影响泄漏值因素的均值化结果；ρ为分辨系数，其取值范围为（0，1），本研究中取0.5。

4）计算关联度

根据式（3）计算比较序列与参考序列之间的关联度（）

将最终关联度结果进行展示，结果见表3。

由表3可知，各因素影响差速器总成泄漏值的关联程度为

X4>X3>X10>X9>X6>X7>X8>X5>X11>X1>X2

本研究选择前5项装配工艺参数（X4、X3、X10、X9、X6）作为影响差速器总成密封质量的关键工艺参数，并将其作为输入变量应用到PSO-BP预测模型中，以达到简化模型结构、提高预测精度的目的。

2 建立BP神经网络预测模型

2.1 BP神经网络

BP神经网络的核心是误差的反向传播过程，其基本思想是采用梯度下降法使误差沿梯度方向下降，经过不断的训练，反复更新神经网络隐藏层的权值和阈值［12］，直到网络的输出结果达到满意的误差精度或者趋近期望值，训练即告停止［13］。BP神经网络结构如图1所示。

BP神经网络训练步骤如下。

1）归一化。为处理数据单位不一致且数值范围相差极大的问题，采取数据归一化方法，将其映射到［0，1］范围内，确保在同一标准尺度进行比较和分析。如式（4）所示。

2）划分样本。选择100组数据作为样本，随机抽取80组样本数据训练BP神经网络，其余20组样本数据作为衡量BP神经网络预测能力的测试集。经由灰色关联分析算法筛选出的右油封压装深度、左油封压装深度、填充螺栓拧紧力矩、排油螺栓拧紧力矩和差壳螺栓拧紧力矩这5项关键装配工艺参数作为BP神经网络的输入，差速器总成泄漏值作为BP神经网络的输出。为进行对比验证，还需训练出不经由灰色关联分析算法简化的BP神经网络，即全部的装配工艺参数作为输入。部分简化后的样本数据见表4。

3）确定隐含层层数。BP神经网络由输入层、输出层、隐藏层组成，其中，输入层和输出层各为一层，而隐藏层可以有一个或多个，尽管多个隐藏层有助于降低训练误差和提升计算的准确性，但这也会导致模型训练时间显著增加，因此，本研究选择使用仅包含单个隐藏层的神经网络结构，隐藏层节点数可以根据式（5）确定［14］。

式中：h为隐藏层节点数；m为输入层个数；n为输出层个数；a为1～10的调节常数。

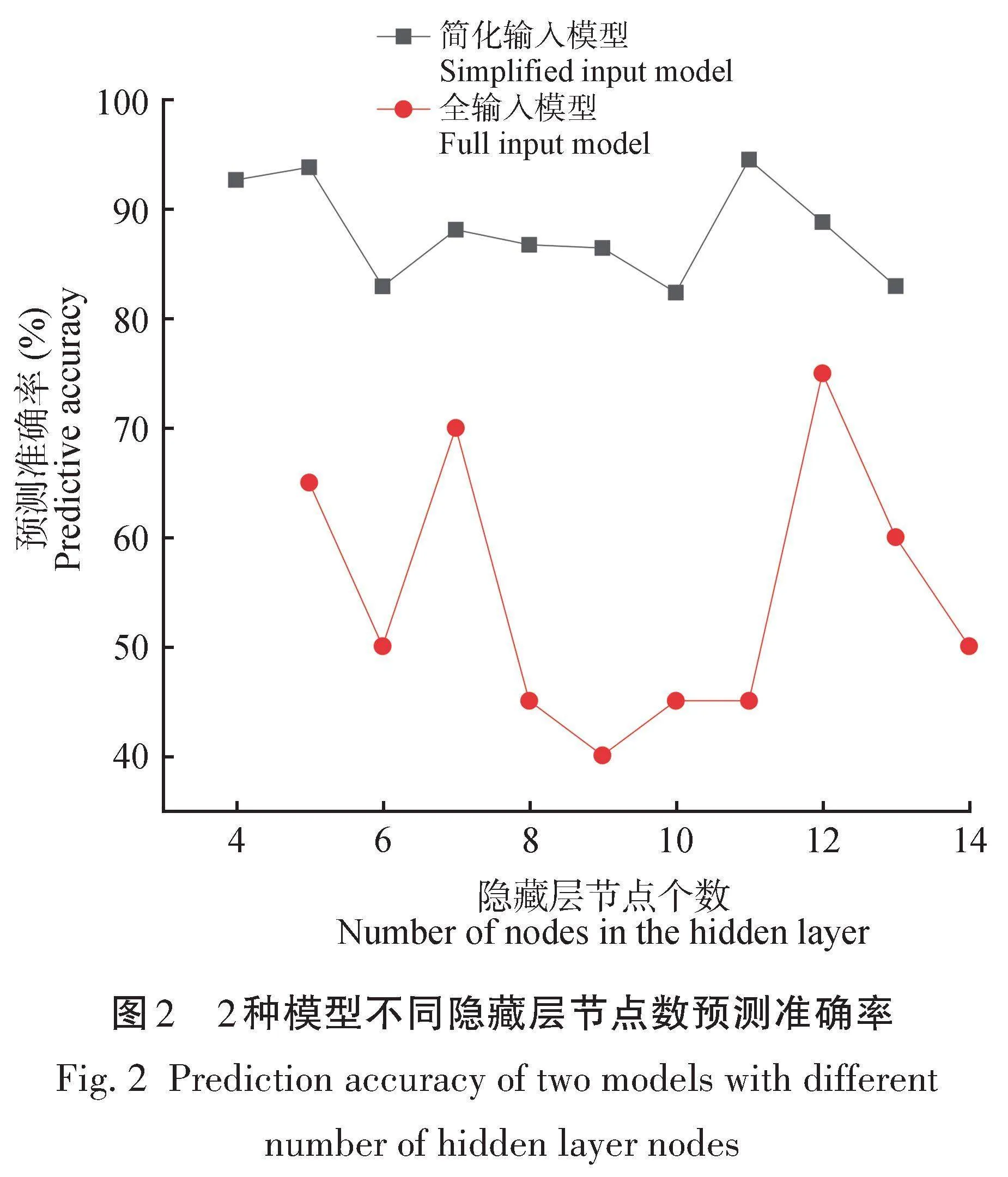
在简化模型中，输入层节点数为5，输出层节点数为1，隐藏层节点数应为4～13的整数；在全输入模型中，输入层节点数为11，输出层节点数为1，隐藏层节点数应为5～14的整数。为了确定最佳隐藏层节点数量，将可能的隐藏层节点数值分别输入到2个模型中，并比较预测结果的准确性。2种模型不同隐藏层节点数对应的预测准确率如图2所示。由图2可知，简化模型的隐藏层节点数取11，全输入模型隐藏层节点数取12时，BP神经网络的预测精度均最高，故确定2种模型的隐藏层节点数分别为11、12。

4）构建BP神经网络。设置训练次数为10 000，学习率为0.01，目标为10-6，运行软件为MATLAB R2022a。

5）训练BP神经网络。

2.2 BP神经网络结果分析

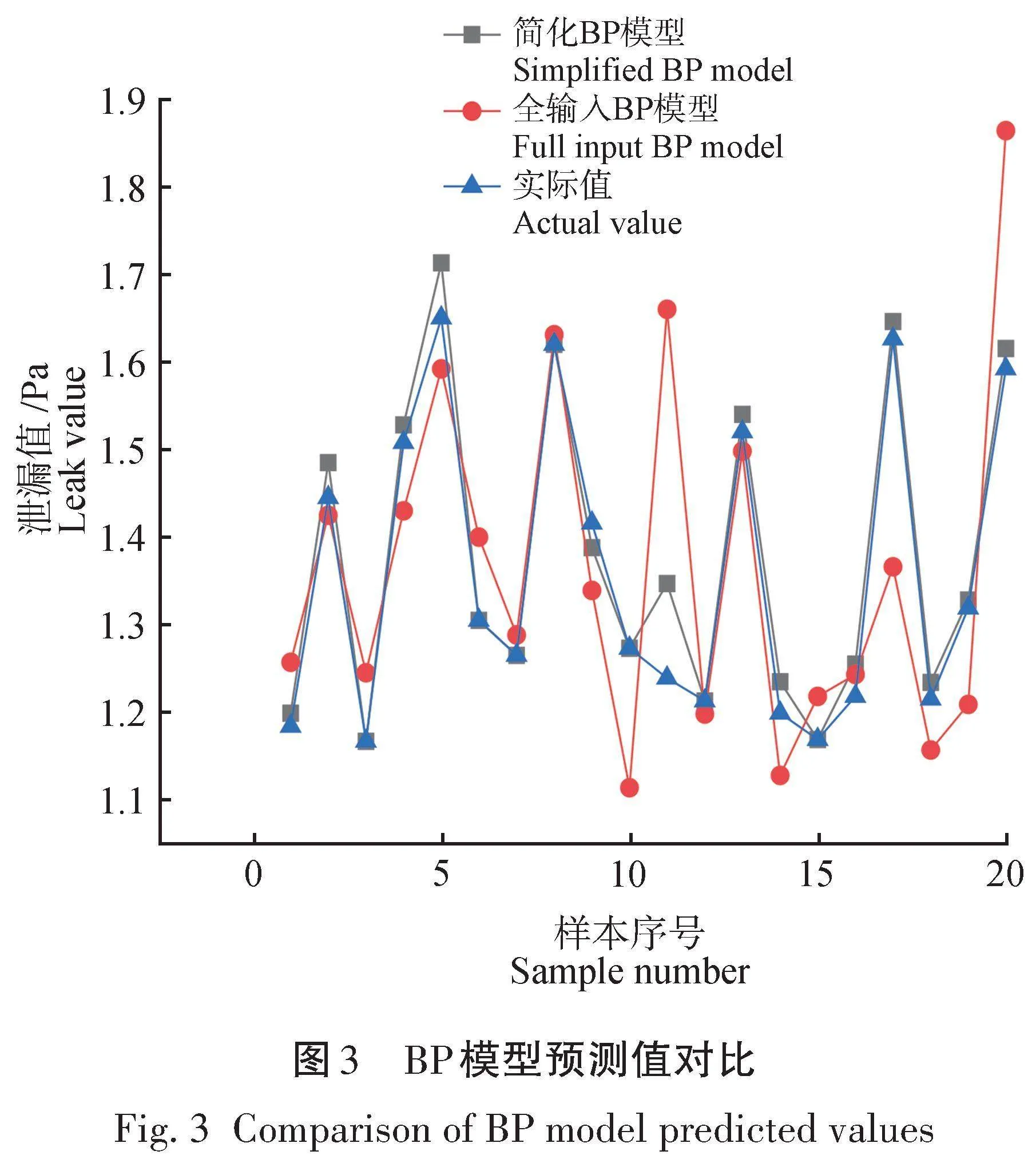
将其余20组数据输入到已经训练完成的BP神经网络中，得到预测值与实际值的对比结果，如图3所示。对预测模型进行综合评价，计算均方根误差（RMSE）、平均绝对误差（MAE）、平均绝对百分比误差（MAPE）、决定系数（R2）等评价指标。

1）均方根误差（RMSE，式中记为RMSE）。均方根误差代表预测值与实际值的偏差，其值越小，表示预测值与实际值之间的差异越小，模型预测精度越高［16］。计算公式为

2）平均绝对误差（MAE，式中记为MAE）。平均绝对误差通过计算实际值与预测值之间差的绝对值来评估模型的准确性。其计算公式为

3）平均绝对百分比误差（MAPE，式中记为MAPE）。其计算公式为

4）决定系数（R2）。决定系数用来评估模型的预测精度，即为描述预测值与实际值之间的相符程度，其值越接近1，表示模型预测效果越好［17］。其计算公式为

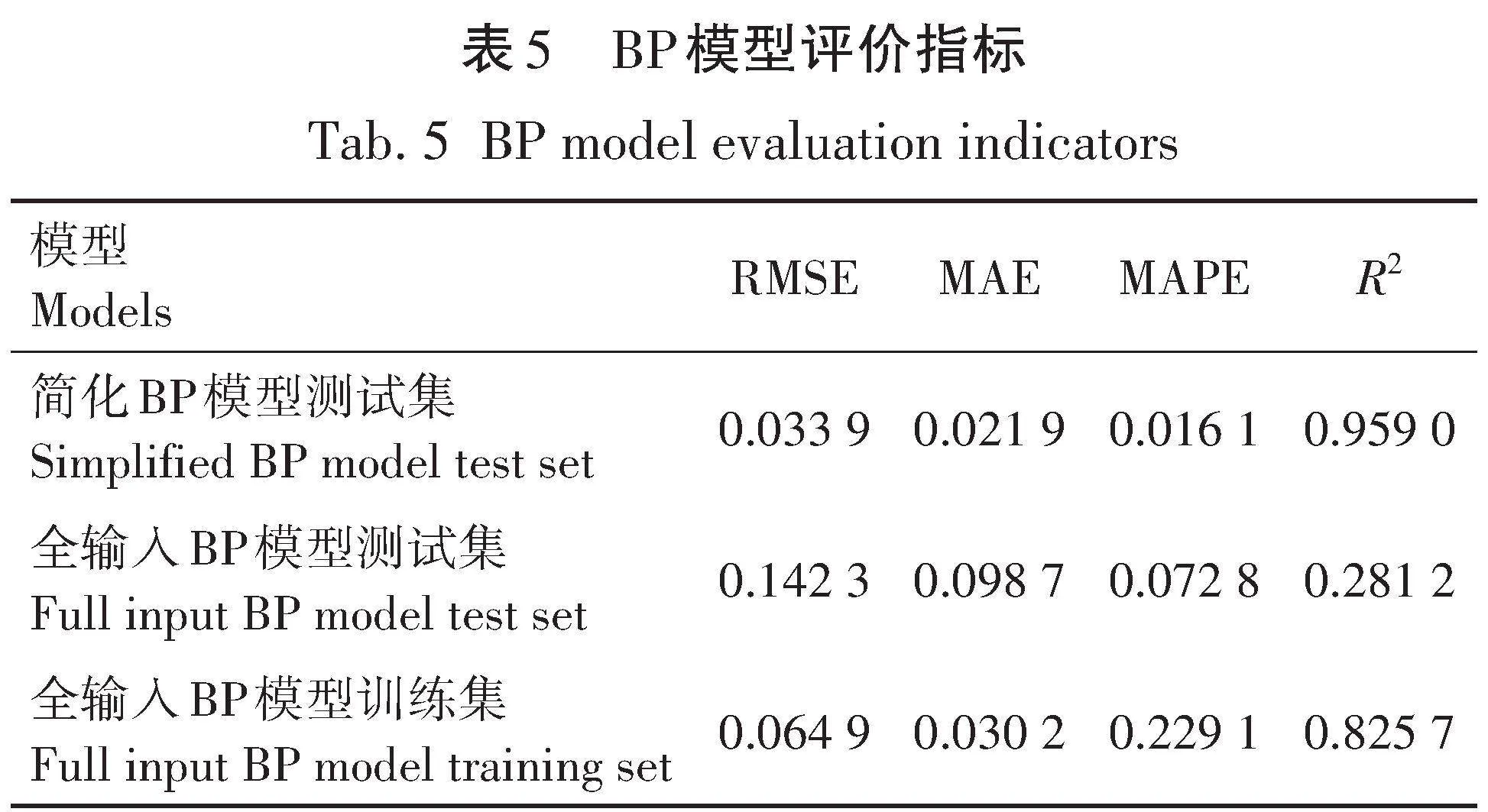
通过图3可直观地看出，简化BP模型的预测效果良好，且通过表5的评价指标对比，可以认为灰色关联分析算法简化BP神经网络的输入层结构可以有效提高模型的训练效率以及预测精度。另外，对比表5中全输入BP模型测试集和训练集的评价指标发现，训练集的性能远超过测试集，此时出现了过拟合问题，模型过度地记住了训练集中的噪声和随机性，以至于失去了泛化能力。为了解决此问题，可以使用粒子群算法优化BP神经网络的权重和偏置，使其更好地拟合训练数据，提高其泛化能力。

虽然BP神经网络具有出色的多维函数映射能力以及较强的分类能力［18］，但是传统的BP神经网络具有一定的局限性，因为BP神经网络的初始权值和阈值是随机产生的，所以其网络稳定性较差，对其进行优化可以提高网络性能［19］。因此，为了克服BP神经网络的局限性，本研究使用粒子群算法来优化BP神经网络。

3 建立PSO-BP神经网络预测模型

3.1 PSO-BP神经网络模型

PSO优化BP神经网络的原理为粒子群算法代替梯度下降法，将BP神经网络的预测误差函数作为适应度函数，粒子不断进行迭代更新以寻找最优位置，并不断更新优化BP神经网络的权值与阈值，当达到预定的迭代次数或误差满足一定条件时，算法终止，确定BP神经网络的最优权值和阈值［20］。其原理如图4所示。

在N维空间中，第i个粒子的位置表示为Xi=（x1，x2，…，xn），第i个粒子的飞行速度表示为Vi=（v1，v2，…，vn），并且每个粒子都有一个适应度值［22］，通过对历史时刻适应度值的比较，可以确定某时刻的个体极值（pbesti）以及群体极值（gbseti），每次迭代过程中，粒子通过个体极值和群体极值按照式（10）和式（11）更新自身的速度和位置［23］。当达到最小误差或最大迭代次数即停止搜索，得到BP神经网络的最优权值与阈值。

式中：r1和r2是在（0，1）之间均匀分布的随机数；c1和c2为学习因子，通常c1=c2=2；ω为惯性因子，其数值的大小决定了算法寻优能力的强弱［24］。

在PSO优化BP神经网络的建模流程中，设置迭代次数为40，种群规模为10，惯性因子ω为0.2，速度为［Vmin，Vmax］=［-1，1］，位置为［Xmin，Xmax］=［-4，4］。运行上述PSO优化BP算法，输出预测结果。

3.2 PSO-BP预测模型结果分析

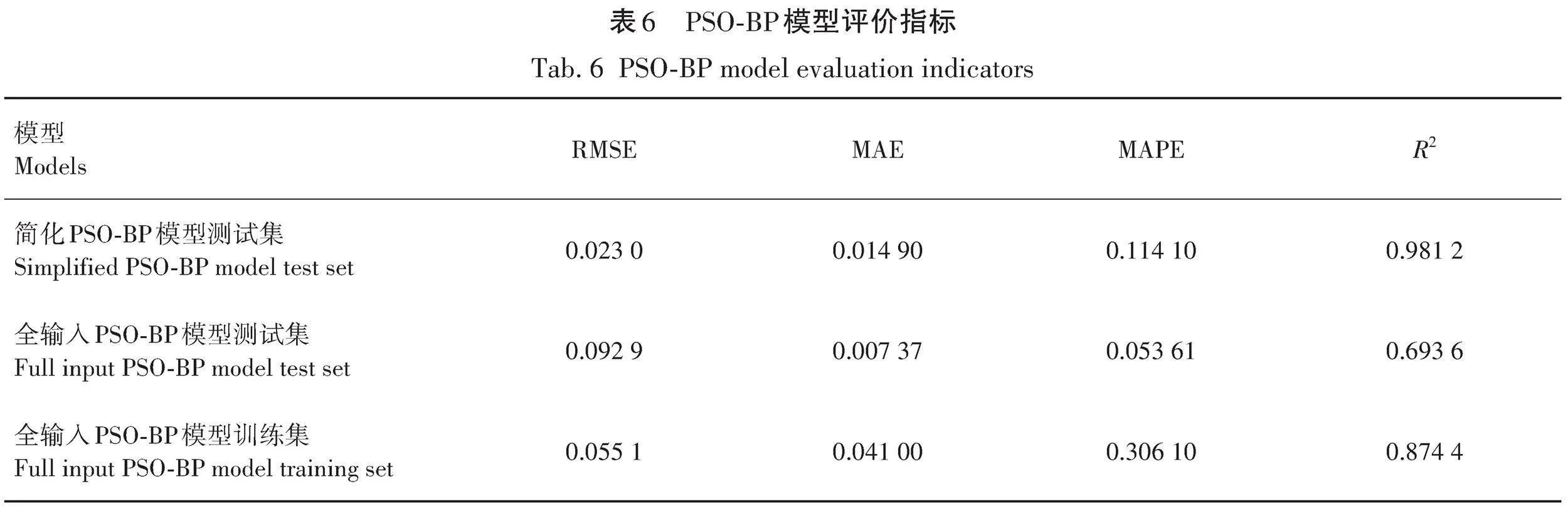
将PSO-BP神经网络进行训练，调用训练完成的PSO-BP神经网络分别对简化样本数据以及全输入样本数据进行预测。预测结果对比如图5所示，评价指标对比见表6。

由图5可以看出，相对于全输入PSO-BP模型，简化PSO-BP模型的预测值更接近实际值，再次验证了由灰色关联分析算法简化输入结构可以提高预测准确率。

3.3 对比验证

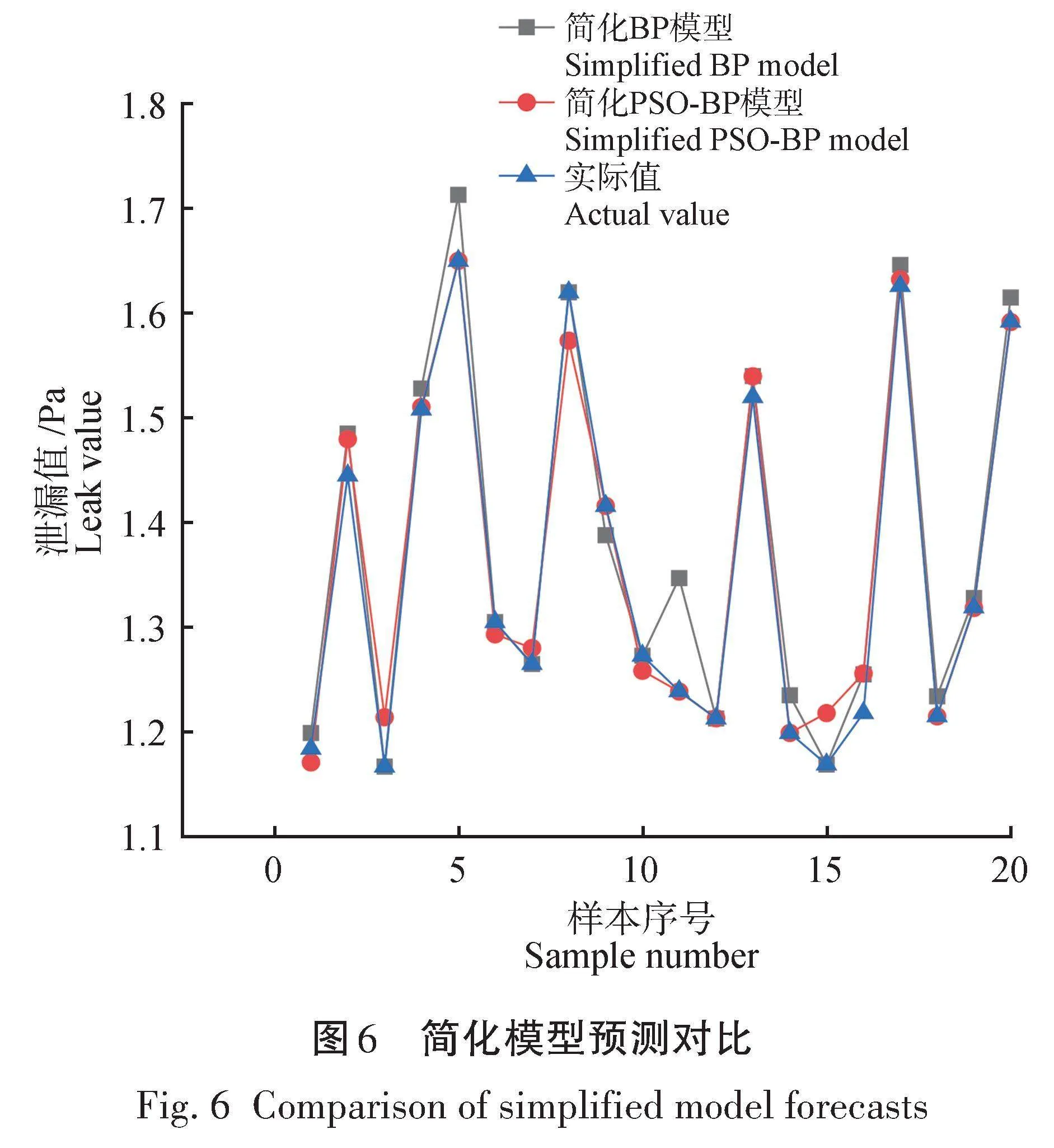
已经验证由灰色关联分析算法简化输入结构可以提高预测准确率，现对比简化后的BP模型以及PSO-BP模型的预测情况，如图6所示，2种简化模型的评价指标对比见表7。

图6中简化PSO-BP模型预测值相较于简化BP模型更接近实际值，并且根据表7中简化PSO-BP模型具有较小的平均相对误差以及均方根误差，决定系数R2最大且接近1，说明该模型拟合优度更高，预测值与实际值的符合程度更高，不会出现过大的偏差，证明PSO优化BP神经网络可以提高其预测精度，同时表7中运行时间的对比也证明了PSO可以提高BP神经网络的预测速度。针对前面提出的BP神经网络出现过拟合的问题，对比2种全输入模型训练集与测试集的评价指标，见表8，由表8发现，全输入PSO-BP模型中训练集与测试集的差距有所减小，由此证明使用粒子群算法优化BP神经网络可以提高其泛化能力。因此，基于其预测精度高、速度快、泛化能力强的特点，可以将PSO-BP神经网络预测模型应用于差速器密封质量预测系统。

4 基于PyQt5的差速器密封质量预测系统

为了对差速器密封质量进行预测并实现质量控制的前瞻性管理，开发一种基于粒子群优化算法和BP神经网络相结合的预测模型。该模型通过融合PSO算法的全局搜索能力与BP神经网络的非线性逼近优势，构建一个高效、准确的差速器密封质量预测系统。采用PyCharm作为主要集成开发环境，结合PyQt5 GUI库的强大功能，提供一个高度用户友好的图形用户界面，可以极大提升用户的操作体验和系统的实用性。其整体架构如图7所示。

差速器密封质量预测系统界面包括导入数据、开始预测和导出文件等多种功能性操作，以及数据可视化显示，实现时间显示、状态判别等多维信息反馈。通过导出文件功能可以在页面上预览相关汇总数据信息以及导出doc/docx文件，满足不同场景下的数据报告需求。该系统利用MES系统收集差速器装配过程中的质量特征数据，并将这些数据作为历史信息存储，通过网络将其传输到差速器密封质量预测系统中，以到达事前预测，提前干预的目的。系统运行实例如图8所示。

由图8系统页面展示的内容可以看出，该系统不仅能准确预测出差速器总成泄漏值，还可以基于历史数据实时分析结果判定质量状态，及时识别和标注异常情况。当系统检测到任何异常状态时，将通过明确的界面提示信息，警告操作人员进行必要的停机检查与维护，这一预警机制可以提升差速器装配的效率和产品质量，并显著减少生产过程中的停机时间和维护成本。

综上，该系统提供了一个实用、高效且用户友好的平台，为差速器装配生产线上的质量管理提供了强有力的支撑。该系统的实施能够为企业带来显著的经济效益以及提升生产效率，具有广泛的应用前景和深远的实际意义。

5 结论

从影响林业运材车差速器密封性能的装配因素出发，利用灰色关联分析算法系统地分析了影响运材车差速器总成密封质量的主要装配工艺参数，即右油封压装深度、左油封压装深度、填充螺栓拧紧力矩、排油螺栓拧紧力矩和差壳螺栓拧紧力矩，以此作为输入变量去训练PSO-BP预测模型。

1）为确定最优隐藏层节点数目，将范围内可能的数据带入到BP神经网络中进行训练，对预测准确率进行对比，确定简化BP神经网络的最佳隐藏层节点数为11，全输入BP神经网络的最佳隐藏层节点数为12。

2）将全部装配工艺数据以及经灰色关联分析算法简化后的数据分别训练BP神经网络，对比结果发现，BP神经网络的预测精度一般且出现过拟合现象，泛化能力一般。故使用粒子群算法优化BP神经网络。

3）对比BP神经网络预测模型以及PSO-BP预测模型，结果显示，PSO-BP预测模型的预测精度更高，泛化能力强，误差范围更小。因此可以将PSO-BP预测模型作为基础设计差速器密封质量预测系统。

4）基于PyQt5 GUI库设计差速器密封质量预测系统，该系统可以直观显示出导入、预测出的数据，状态正常与否，并对异常状态进行标注以达到预警作用。

综上，该模型可以较为精确地预测出差速器总成泄漏值，有利于直观显示出差速器总成密封质量合格与否。使用该预测模型可以实现对差速器装配过程的事前控制，为林业运材车辆的维护和管理提供科学依据，不仅提高了林业运材车差速器的维护效率，还为其他车辆差速器装配的质量控制提供了参考。

【参 考 文 献】

［1］ 唐志国.木材生产作业机械设备及汽车运材管理的探讨［J］.科技创新与应用，2013（15）：275.

TANG Z G.Discussion on the management of mechanical equipment and automobile timber transportation for timber production operations［J］.Technology Innovation and Application，2013（15）： 275.

［2］ 周玉甲.汽车差速器齿套冷锻工艺分析与优化［J］.锻压技术，2023，48（10）：24-30.

ZHOU Y J.Analysis and optimization on cold forging process for automotive differential gear sleeve［J］.Forging & Stamping Technology，2023，48（10）：24-30.

［3］ 方群霞，姜思佳，杨娟.基于PSO-BP神经网络优化的汽车斗框注塑成型优化［J］.塑料，2020，49（5）：129-134.

FANG Q X，JIANG S J，YANG J.Injection molding optimization of car bucket frame based on PSO-BP neural network［J］.Plastics，2020，49（5）：129-134.

［4］ WEI L X，ZHANG Y，JI L L，et al.Pressure drop prediction of crude oil pipeline basex6TBZeCPCUNPMNYk9clYtA==d on PSO-BP neural network［J］.Energies，2022，15（16）：5880.

［5］ 方喜峰，于超，章振，等.基于支持向量机的船用柴油机装配质量预测［J］.组合机床与自动化加工技术，2021（9）：62-66.

FANG X F，YU C，ZHANG Z，et al.Research on assembly quality prediction method of marine diesel engine based on support vector machine［J］.Modular Machine Tool & Automatic Manufacturing Technique，2021（9）：62-66.

［6］ 孟冠军，张磊，马存徽.基于孪生数据的产品装配过程质量预测模型［J］.组合机床与自动化加工技术，2022（3）：126-129.

MENG G J，ZHANG L，MA C H.Quality prediction model of product assembly process based on twin data［J］.Modular Machine Tool & Automatic Manufacturing Technique，2022（3）：126-129.

［7］ HU D，HU Y J，YI S，et al.Prediction method of surface settlement of rectangular pipe jacking tunnel based on improved PSO-BP neural network［J］.Scientific Reports，2023，13（1）：5512.

［8］ 陈资，陈春雨，张根保.基于GA-SVM的数控机床装配质量预测模型［J］.制造技术与机床，2021（9）： 97-100，106.

CHEN Z，CHEN C Y，ZHANG G B.Assembly quality prediction model of CNC machine tools based on GA-SVM［J］.Manufacturing Technology & Machine Tool，2021（9）：97-100，106.

［9］ 董海，黄佳慧.基于状态空间模型的废旧机床再制造装配过程质量预测［J］.组合机床与自动化加工技术，2020（11）：11-14，19.

DONG H，HUANG J H.Quality prediction of re-manufacturing and assembling process of waste machine tools based on state space model［J］.Modular Machine Tool & Automatic Manufacturing Technique，2020（11）：11-14，19.

［10］ SHEN L B，TIAN L P.A static load position identification method for optical fiber-composite structures based on particle swarm optimization-back propagation neural network algorithm［J］.MeasurWEm/Rmlteu/WSBQ2uIpkBWPLx/eozYIMfbZRlTDQqbk=ement and Control： Journal of the Institute of Measurement and Control，2023，56（3/4）：820-831.

［11］ 周康渠，张朝武，屈清，等.M型变速箱总成密封质量预测方法研究［J］.工业工程，2022，25（2）： 22-27，41.

ZHOU K Q，ZHANG C W，QU Q，et al.A research on the prediction method of sealing quality of M-type gearbox assembly［J］.Industrial Engineering Journal，2022，25（2）：22-27，41.

［12］ LU G Y，XU D，MENG Y.Dynamic evolution analysis of desertification images based on BP neural network［J］.Computational Intelligence and Neuroscience，2022，2022：5645535.

［13］ 万芯炜，王晶，杨辉，等.BP神经网络结合粒子群优化卡尔曼滤波的MEMS陀螺随机误差补偿方法［J］.兵工学报，2023，44（2）：556-565.

WAN X W，WANG J，YANG H，et al.A random error compensation method of MEMS gyroscope based on BP neural network combined with PSO-Optimized Kalman filter［J］.Acta Armamentarii，2023，44（2）：556-565.

［14］ 赵月悦.基于遗传算法优化神经网络的岩质陡坡桥梁桩基承载力预测方法［J］.自动化技术与应用，2022，41（10）：32-35.

ZHAO Y Y.Prediction method of bearing capacity of bridge pile foundation on steep rock slope based on neural network optimized by genetic algorithm［J］.Techniques of Automation and Applications，2022，41（10）：32-35.

［15］ 陈远玲，陈浩楠，王肖，等.基于PSO-BP的甘蔗联合收割机物流堵塞预测预警研究［J］.广西大学学报（自然科学版），2023，48（3）：662-673.

CHEN Y L，CHEN H N，WANG X，et al.Prediction and early warning research on logistics blockage of sugarcane combine based on PSO-BP［J］.Journal of Guangxi University（Natural Science Edition），2023，48（3）：662-673.

［16］ 顾春生，唐鑫，朱常坤，等.基于主成分分析法优化神经网络的滆湖组黏性土抗剪强度预测［J］.科学技术与工程，2023，23（28）：11980-11989.

GU C S，TANG X，ZHU C K，et al.Prediction of shear strength of cohesive soil in Gehu formation based on back propagation neural network optimized by principal component analysis［J］.Science Technology and Engineering，2023，23（28）：11980-11989.

［17］ 崔树银，汪昕杰.基于特征工程的集成学习短期光伏功率预测［J］.科学技术与工程，2022，22（2）：532-539.

CUI S Y，WANG X J.Short-term photovoltaic power prediction by ensemble learning based on feature engineering［J］.Science Technology and Engineering，2022，22（2）：532-539.

［18］ 向星宇，刘敬之，曲全磊，等.基于RF-PSO-BP的电能质量稳态指标预测［J］.电子设计工程，2023，31（22）：116-120.

XIANG X Y，LIU J Z，QU Q L，et al.Power quality steady state index prediction based on RF-PSO-BP［J］.Electronic Design Engineering，2023，31（22）：116-120.

［19］ 苏佳，杨泽超，易卿武，等.基于遗传算法优化BP神经网络的GNSS干扰源定位技术［J］.无线电工程，2024，54（5）：1175-1182.

SU J，YANG Z C，YI Q W，et al.GNSS interference source localization technology based on genetic algorithm optimized BP neural network［J］.Radio Engineering，2024，54（5）：1175-1182.

［20］ 常瑞莉.一种基于BP神经网络的移动通信网络故障检测方法［J］.自动化技术与应用，2023，42（6）：123-126.

CAHNG R L.Fault detection method of mobile communication network based on BP neural network［J］.Techniques of Automation and Applications，2023，42（6）：123-126.

［21］ 崔峰，王汉封，舒卓乐.基于PSO-BP神经网络的隧道内气动压力幅值预测［J］.中南大学学报（自然科学版），2023，54（9）：3752-3761.

CUI F，WNAG H F，SHU Z L.Prediction of aerodynamic pressure amplitude in tunnel based on PSO-BP neural network［J］.Journal of Central South University：Natural Science Edition，2023，54（9）：3752-3761.

［22］ 宋栓军，陈凯凯，张华威.基于APSO算法的双容水箱PID参数优化仿真［J］.计算机仿真，2018，35（8）：261-265.

SONG S J，CHEN K K，ZHANG H W.Optimization of PID control of liquid level control of double-tank based on improved particle swarm optimization algorithm［J］.Computer Simulation，2018，35（8）：261-265.

［23］ 黄志滨，陈桪.基于PSO-GA算法的无人机集群森林火灾探查方法［J］.计算机工程与应用，2023，59（9）：289-294.

HUANG Z B，CHEN X.UAV cluster forest fire detection method based on PSO-GA algorithm［J］.Computer Engineering and Applications，2023，59（9）：289-294.

［24］ 韩斌，吉坤，胡亚飞，等.ANN-PSO-GA模型在湿喷混凝土强度预测及配合比优化中的应用［J］.采矿与安全工程学报，2021，38（3）：584-591.

HAN B，JI K，HU Y F，et al.Application of ANN-PSO-GA model in UCS prediction and mix proportion optimization of wet shotcrete［J］.Journal of Mining & Safety Engineering，2021，38（3）：584-591.