北方森林乔木层碳储量的估计及空间分析

摘 要：利用遥感的方式对森林乔木层碳储量（Aboveground Biomass Carbon Stocks，ABGCS）以及乔木层碳储量的光饱和值进行精准估测，以期替代传统大面积调查的繁琐工序，为碳储量的估测提供参考和依据，提高森林可持续经营管理的效率。以2017年黑龙江省伊春市嘉荫县森林乔木层碳储量（ABGCS）作为研究对象，利用Landsat8 OLI遥感影像以及森林资源二类调查数据，构建参数模型多元逐步回归模型（Stepwise Multiple-Regression，SMR），非参数模型BP神经网络模型（BP neural network，BP-NN）、随机森林模型（Random Forest，RF）、支持向量回归模型（Support Vector Machine，SVR）对嘉荫县地区ABGCS进行估测和反演其空间分布情况。研究结果表明，非参数模型的估测精度明显高于参数模型，其中3种非参数模型（BP-NN、RF、SVR）相较于参数模型（SMR），拟合精度分别提高了25.0%、12.2%、7.3%；综合比较4种模型十折交叉验证的评价指标，分析得出模型性能优劣为BP-NN>RF>SVR>SMR，其中BP-NN模型拟合出最大的决定系数（R2为0.785）和最小的均方根误差（RMSE为3.572 t/hm2）、均方误差（MSE为12.757 t/hm2）、平均绝对误差（MAE为2.687 t/hm2）；从碳储量残差分段检验结果来看，4种模型均存在碳储量不同程度上高值低估和低值高估的情况，BP-NN模型在各碳储量分段的平均残差（ME）和相对平均残差（MRE）值均为最小，其泛化能力较强；利用立方项模型确定ABGCS的光饱和值为63.056 t/hm2，与BP-NN所预测的ABGCS光饱和值接近（64.232 t/hm2）。因此，BP-NN模型在估测嘉荫县ABGCS具有较为理想的效果，为森林碳储量动态监测及研究提供重要依据。

关键词：遥感； 森林乔木层碳储量； 光饱和值； BP神经网络模型； 立方项模型

中图分类号：S757.2 文献标识码：A DOI：10.7525/j.issn.1006-8023.2024.04.015

Estimation and Spatial Analysis of Carbon Storage in Tree Layers of Northern Forests

LIU Lei， JIA Weiwei*， ZHANG Xiaoyong， HE Jinyou， WU Simin， LU Shixin， LIANG Yuepeng

（College of Forest， Northeast Forestry University， Harbin 150040，China）

Abstract： Using remote sensing methods to accurately estimate aboveground biomass carbon stock （ABGCS） in forest canopy layers and light saturation value of carbon storage， aiming to replace the cumbersome procedures of traditional large-area surveys， providing references and basis for carbon storage estimation， and improving the efficiency of sustainable forest management. In this study， the ABGCS in Jiayin County， Yichun City， Heilongjiang Province in 2017 was selected as the research object. Landsat 8 OLI remote sensing images and forest resource two-class survey data were used to construct parameter models of stepwise multiple regression model （SMR）， non-parameter models of BP neural network model （BP-NN）， random forest model （RF）， support vector regression model （SVR） to estimate and reverse the spatial distribution of ABGCS in Jiayin County. The research results showed that the estimation accuracy of non-parameter models was significantly higher than that of parameter models. Among them， the fitting accuracy of the three non-parameter models （BP-NN， RF， SVR） was increased by 25.0%， 12.2%， and 7.3%， respectively， compared with the parameter model （SMR）. By comprehensive comparison of the evaluation indexes of the four models in ten-fold cross-validation， the performance of the models was analyzed： BP-NN>RF>SVR>SMR， among which the BP-NN model fitted the largest R2 （0.785） and the smallest RMSE （3.572 t/hm2）， MSE （12.757 t/hm2）， MAE （2.687 t/hm2）. From the perspective of carbon storage residual segmentation test results， all four models exhibited varying degrees of overestimation and underestimation of carbon storage. The BP-NN model had the smallest ME and MRE values in each carbon storage segment， indicating strong generalization ability. The light saturation value of ABGCS was determined to be 63.056 t/hm2 using a cubic model， which was close to the predicted ABGCS light saturation value by BP-NN （64.232 t/hm2）. Therefore， the BP-NN model has a relatively ideal effect in estimating ABGCS in Jiayin County， providing important basis for dynamic monitoring and research of forest carbon storage.

Keywords： Remote sensing； aboveground biomass carbon stock； light saturation value； backpropagation neural network model （BP-NN）； cubic mode

0 引言

森林生态系统在维护区域生态环境和全球碳平衡方面发挥着非常关键且不可替代的作用。森林生态系统作为动态碳库，其碳储量不仅受整个森林生态系统植被面积的影响，还受森林植被碳储量密度的质量，即单位面积森林碳储量的影响［1-2］。因此，对精准估测森林碳储量以及了解其空间分布的研究具有重要意义。然而，对森林碳储量估测的不确定性问题，以及如何精确量化森林碳储量，是一项重大挑战［3］。

研究森林碳储量，必须对其进行量化，国内外的很多学者已经就此问题给出了很多的方法，已有多种研究手段被用于估算局部、区域和世界范围的森林碳储量［4-5］。传统上，使用样地测量森林结构参数可以提供准确的信息，但需要大量的人力和物力。当森林结构复杂时，如热带森林，无法进行森林原位监测［6］。遥感估测碳储量相较于样地实测具有多项优势，包括成本较低、实时性高、高精度、非破坏性和适用于大规模动态监测等［7］。通过高分辨率遥感影像收集详细的植被信息，如植被指数和纹理特征等。这些数据通常用于参数或非参数估计方法，通过构建数学模型，结合遥感信息和地面调查数据，最终利用分析公式进行森林碳储量估算，随后可分析森林碳储量的空间分布和动态。与参数模型相比，非参数模型具有更强的数据拟合能力和更高的估测精度。然而，非参数模型对样本量的大小和代表性更为敏感，对于样本量较小的研究区来说，改进森林碳储量的估计效果有限［8-9］。基于遥感的森林碳储量估测常使用多种遥感估算经验模型。其中，一些主要的模型包括多元逐步回归模型、地理加权模型、支持向量回归模型、人工神经网络法和随机森林回归等［10］。

本研究具体目标如下。1）通过地面实测数据计算嘉荫县森林乔木层碳储量（Aboveground Biomass Carbon Stocks，ABGCS），通过处理Landsat 8 OLI遥感影像并提取相关遥感因子，进而筛选出与ABGCS显著相关的遥感因子；2）构建多元逐步回归模型（Stepwise Multiple-Regression，SMR）、BP神经网络模型（BP neural network，BP-NN）、随机森林模型（Random Forest，RF）和支持向量回归模型（Support Vector Machine，SVR），并对比分析模型对ABGCS的估测能力；3）利用立方项模型对森林乔木层碳储量的光饱和值进行估算，并利用最优回归模型的结果对所预测光饱和值进行检验；4）对嘉荫县地区ABGCS进行反演和空间分布的分析。

1 研究区概况

研究区位于黑龙江省伊春市嘉荫县，地处于小兴安岭北麓东段，地理坐标为48°8′30″～49°26′5″N， 129°9′45″～130°50′E。全区属于温带大陆性季风气候，年平均气温-1.5～-0.7 ℃。降水主要分布在夏季，年均降水量通常在400～600 mm。该地区地势较高，地理条件多为丘陵和山区。森林覆盖率达78.3%，森林地面积60.71 万hm2，森林资源主要包括落叶松林、针阔叶混交林和阔叶混交林。

2 数据与方法

2.1 数据来源及处理

2.1.1 样地数据

基于2017年嘉荫县13个经营林区的森林资源二类调查数据，包括海拔、植被类型、优势树种和各小班每公顷蓄积量等，剔除蓄积量为0 m3的小班，并去除非植被的小班。最终在SPSS 26中采用系统抽样的方法抽取984块小班。

2.1.2 森林乔木层碳储量（ABGCS）计算

以主要的优势树种（树种组）为对象，根据筛选出984块样地的每公顷蓄积量，进行森林生物量与碳储量的计算。目前，国际上对森林碳储量的估算方法通常采用生物量与生物碳含量的乘积。本研究采用了Fang等［11］提出的生物量转换因子连续函数法，以估计黑龙江省主要森林类型的生物量。公式为

B=aV+b。 （1）

C=B×C_c。 （2）

式中：B为某一树种单位面积生物量，mg/hm2；V为某一树种单位面积蓄积量，m3/hm2；a和b为蓄积量与生物量转换参数；C为碳储量，t/hm2；C_c为含碳系数。黑龙江省各类森林的生物量与蓄积量转换参数见表1［12］。使用国际上普遍采用的含碳系数0.5来估算森林碳储量［13］。

2.1.3 遥感影像数据获取及处理

为确保影像信息与地面调查信息尽可能一致，选用2017年7月获取的Landsat 8 OLI卫星影像数据（条带号116/26、117/26），该影像完整地覆盖了整个嘉荫县。

首先利用ENVI5.3软件，对原始影像进行辐射定标、大气校正和影像裁剪等处理。之后使用波段计算工具Bandmath提取所需的各种遥感因子，包括原始波段、植被指数、纹理特征和主成分分析等，部分重要遥感变量计算公式见表2。在本研究中，地形因子使用ArcGIS 10.8空间和统计分析扩展来提取，包括高程、起伏程度、粗糙程度、坡度和坡向等。最后将提取的地形因子和遥感因子在SPSS 26中进行标准化处理。

2.2 森林乔木层碳储量遥感模型

2.2.1 多元线性逐步回归模型（SMR）

利用SPSS 26，采用Pearson相关系数对特征变量（遥感因子、地形因子）与森林乔木层碳储量进行相关性分析。在此过程中，剔除相关性不显著的变量，选择P≤0.05且方差膨胀因子（Variance Inflation Factor，VIF）小于10的特征变量，排除特征变量间的多重共线性［14］。最后，通过多元逐步回归确定参与建模的自变量最佳组合，具体方程为

y=β_0+β_1 x_1+β_2 x_2+...+β_m x_m。 （3）

式中：y为单位面积森林乔木层碳储量，t/hm2；x_1，x_2，…，x_m为影响碳储量的自变量因子；β_1，β_2，…，β_m为相应的回归系数；β_0为残差项。

2.2.2 支持向量回归模型（SVR）

本研究中，SVR模型采用的是高斯核函数（Radial Basis Function，RBF）。对于SVR模型，最重要是对RBF核参数gamma（g）和惩罚系数cost（c）的选择，其大小直接影响了模型预测的准确度［15］。运用Python 3.11，根据研究目标，选用sklearn中的网格搜索和交叉验证函数GridSearchCV（CV），设置调优的参数范围，核参数（g）的范围是［0.001，0.01，0.1，1］，惩罚系数（c）的范围是［0.01，0.1，1，10］，其中交叉验证（CV）为10，以此来寻求最优的参数组合。

2.2.3 随机森林模型（RF）

随机森林是一种基于装袋（Bagging）的集成学习方法，其他使用决策树作为基本学习器，通过数据重采样（Bootstrap Aggregating）构建多个基学习 器并将其预测结果组合生成随机森林模型。预测结果为n棵决策树预测结果的平均值［16］。本研究使用R语言中的随机森林模型包进行装袋法估计。RF模型的构建涉及2个重要的超参数，决策树的数目（ntree，式中记为ntree）和随机抽取的决策树节点变量个数（mtry，式中记为mtry）。一般情况下，随机森林回归模型建议将mtry设置为总特征数量的1/3、ntree需要确保整体随机森林的误差趋于稳定即可［17］。在模型的构建过程中加入主成分分析，找到数据中最重要的特征或主成分，并将数据投影到这些主成分上，以实现数据降维。这有助于减少数据的复杂性，去除冗余信息，同时保留尽可能多的方差。

2.2.4 BP神经网络模型（BP-NN）

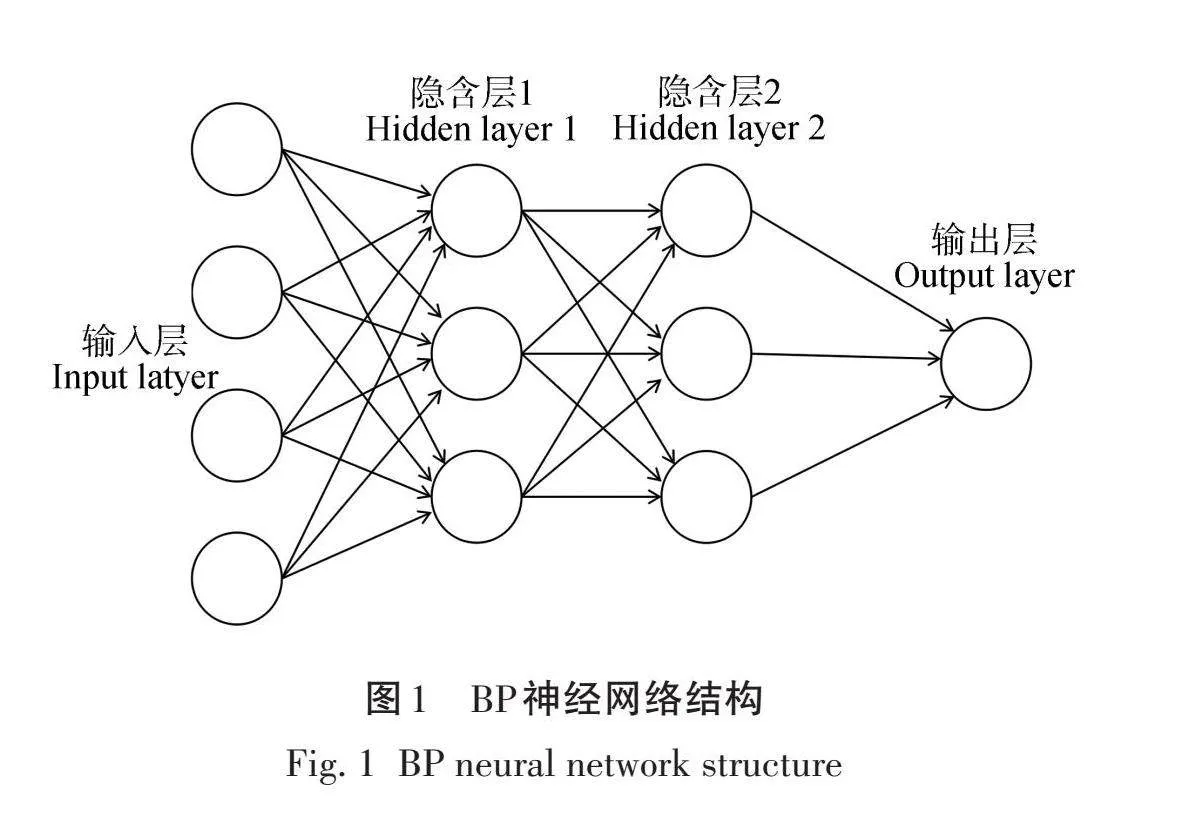
BP神经网络是一种多层神经网络，通常包含输入层、一个或多个隐含层和输出层，如图1所示。BP神经网络的核心特点是使用反向播算法来训练网络，以减小模型的预测误差。

要创建最佳BP神经网络模型，需要不断优化关键参数，包括网络结构（层数和隐含层节点数）、权值和阈值的初始化、最大训练迭代次数、学习率和学习速率等［18］。本研究采用含有2个隐含层的三层BP神经网络模型，输入层神经元的个数为通过相关性分析，并纳入多元逐步回归模型的特征因子个数，输出层神经元个数为1。为在确保模型精度的前提下，防止过拟合并提高模型的泛化能力，本研究选择尽可能减少隐含层神经元的数量［19］。基于经验式（4）确定隐含层神经元的范围［20］。双隐含层节点数配置使用嵌套循环来迭代所确定隐含层神经元范围之间所有整数的大小组合，通过比较R2大小，确定双隐含层节点的最优配置。最后，将最优的参数组合带入模型中，对ABGCS进行预测。

w=√（n+m）+a。 （4）

式中：w为隐含层神经元个数；n为输入层神经元个数；m为输出层神经元个数；a为1～10的常数。

2.3 模型评价与检验

2.3.1 模型评价

基于十折交叉验证的决定系数（R2）、均方根误差（RMSE，式中记为RMSE）、均方误差（MSE，式中记为MSE）和平均绝对误差（MAE，式中记为MAE）4种指标对模型的估测能力进行评价与检验，如式（5）—式（8）所示。

R^2=1-（∑_（i=1）^n▒（y_i-y ̂_i ）^2 ）/（∑_（i=1）^n▒（y_i-¯（y_i ））^2 ）。 （5）

R_MSE=√（（∑_（i=1）^n▒（y_i-y ̂_i ）^2 ）/n）。 （6）

M_SE=1/n ∑_（i=1）^n▒（y_i-y ̂_i ）^2 。 （7）

M_AE=1/n ∑_（i=1）^n▒|y_i-y ̂_i | 。 （8）

式中：y_i为实测值；¯（y_i ）为样本平均值；y ̂_i为估测值；n为样本容量；i为样本点。

2.3.2 残差分段检验

本研究采用“刀切法”残差检验，采用相对平均残差（MRE，式中记为MRE）、平均残差（ME，式中记为ME）2个度量标准对样本进行分段残差分析，如式（9）—式（10）所示。分别设置30～50、50～70、70～90 t/hm2 3个碳储量分段。通过分段残差检验，分析不同碳储量分段下不同模型之间的残差差异。

M_E=1/n ∑_（i=1）^n▒（y_i-y ̂_i ） 。 （9）

M_RE=1/n ∑_（i=1）^n▒〖（（y_i-y ̂_i）/y_i ）〗×100%。 （10）

2.4 碳储量光饱和点确定

通过选择与实测的乔木层碳储量相关性最高的波段，建立散点图，研究发现通常情况下，随着碳储量的增加，波段反射率呈降低趋势。然而，一旦碳储量达到一定水平，光谱反射率就不再发生显著变化。该水平值是通过光学遥感估算碳储量时的光饱和点。本研究采用参数估计方法探寻乔木层碳储量的光饱和点［21］。研究表明，二次项模型和立方项模型能够较好地拟合曲线方程，如式11所示，这有助于更准确地描述数据的非线性关系［21-22］。通过计算该函数的拐点值，以确定光学遥感估测ABGCS的光饱和点。

f（g）=x_n g^n+x_（n-1） g^（n-1）+x_（n-2） g^（n-2）+…+x_（^2 ） g^2+x_（^1 ） g+x_0 （a_n≠0）。 （11）

式中：f（g）为g模型拐点值；x_n为模型参数；非负整数n为模型的次数（本研究n取2和3）。

2.5 研究区森林乔木层碳储量反演

使用反距离加权空间插值法（Inverse Distance Weighted，IDW），对实测以及4种模型预测的嘉荫县森林乔木层碳储量的空间分布情况进行反演。由于森林的复杂性和内在的不确定性因素，运用统计学方法来探究研究区内样地之间的空间分布结构是一种必然趋势。通过ArcGIS10.8软件中的插值工具，对森林乔木层碳储量进行反演，绘制研究区域的地貌图，对不同地貌下的碳储量进行空间分析。

3 结果与分析

3.1 建模因子筛选结果

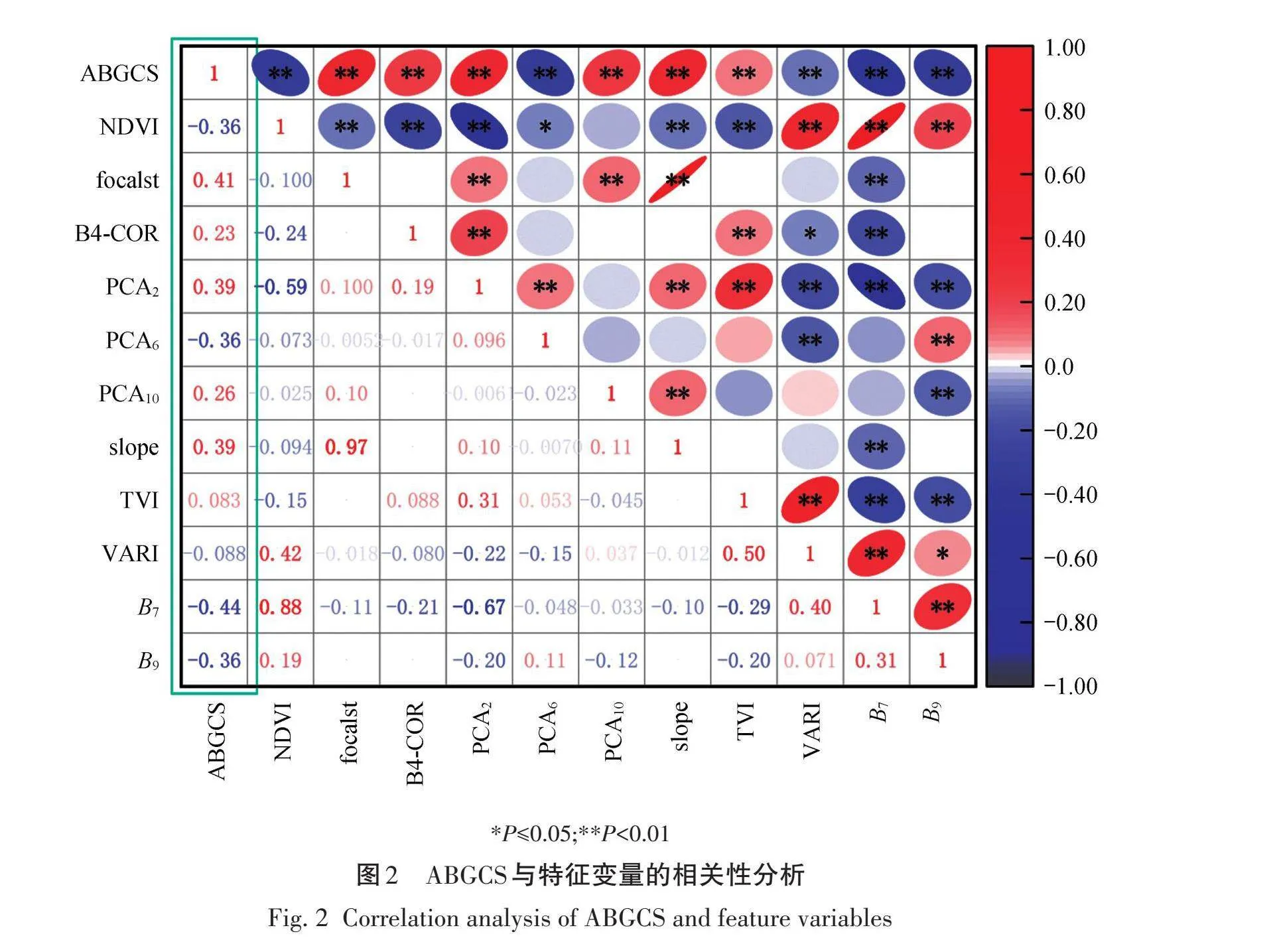
利用SPSS 26将特征变量进行标准化，采用逐步回归方法进行最优变量选择，最终选取植被指数因子3个（NDVI、TVI、VARI）、主成分分析因子3个（PCA2、PCA6、PCA10）、原始波段因子2个（B7、B9）、纹理特征因子1个（B4-COR）、地形因子2个（slope、focalst）共计11个特征变量，其在P<0.01水平上表现出极显著的相关性，如图2所示，其中，B7相关性最高，R=-0.44。

3.2 森林乔木层碳储量估测模型构建结果

3.2.1 多元线性逐步回归模型构建结果

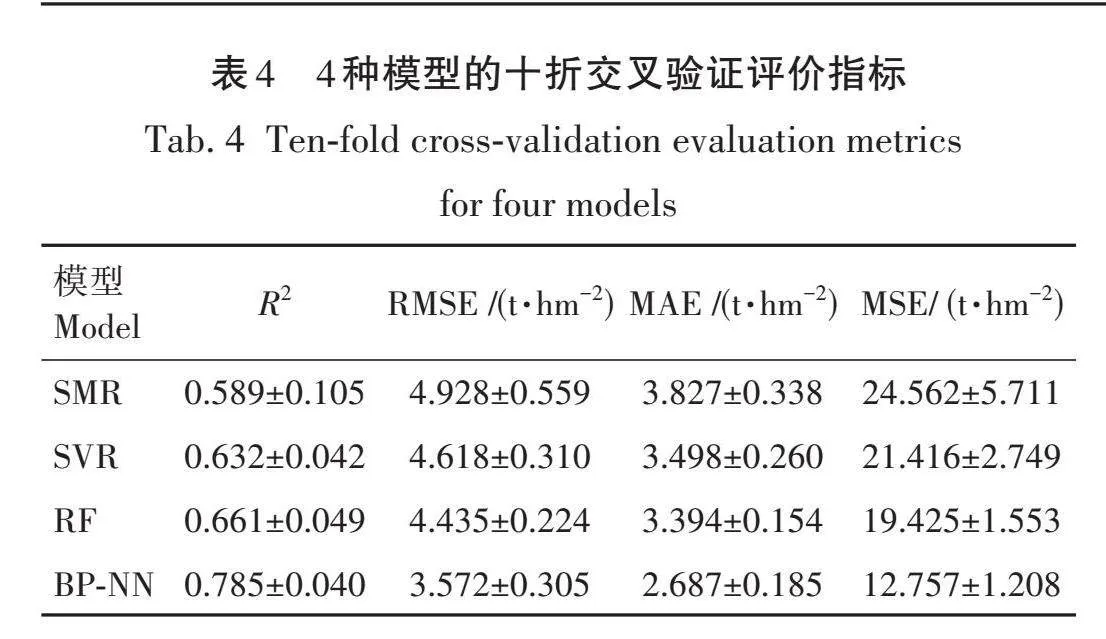
借助R语言构建多元线性逐步回归模型，引入程序包caret进行十折交叉验证，其拟合结果见表3。由表3可知，SMR模型能够解释嘉荫县森林乔木层碳储量的决定系数58.9%，RMSE、MSE和MAE的值相对较小，说明模型在预测上取得了一定的准确性，但仍有改进的空间。

3.2.2 支持向量回归模型构建结果

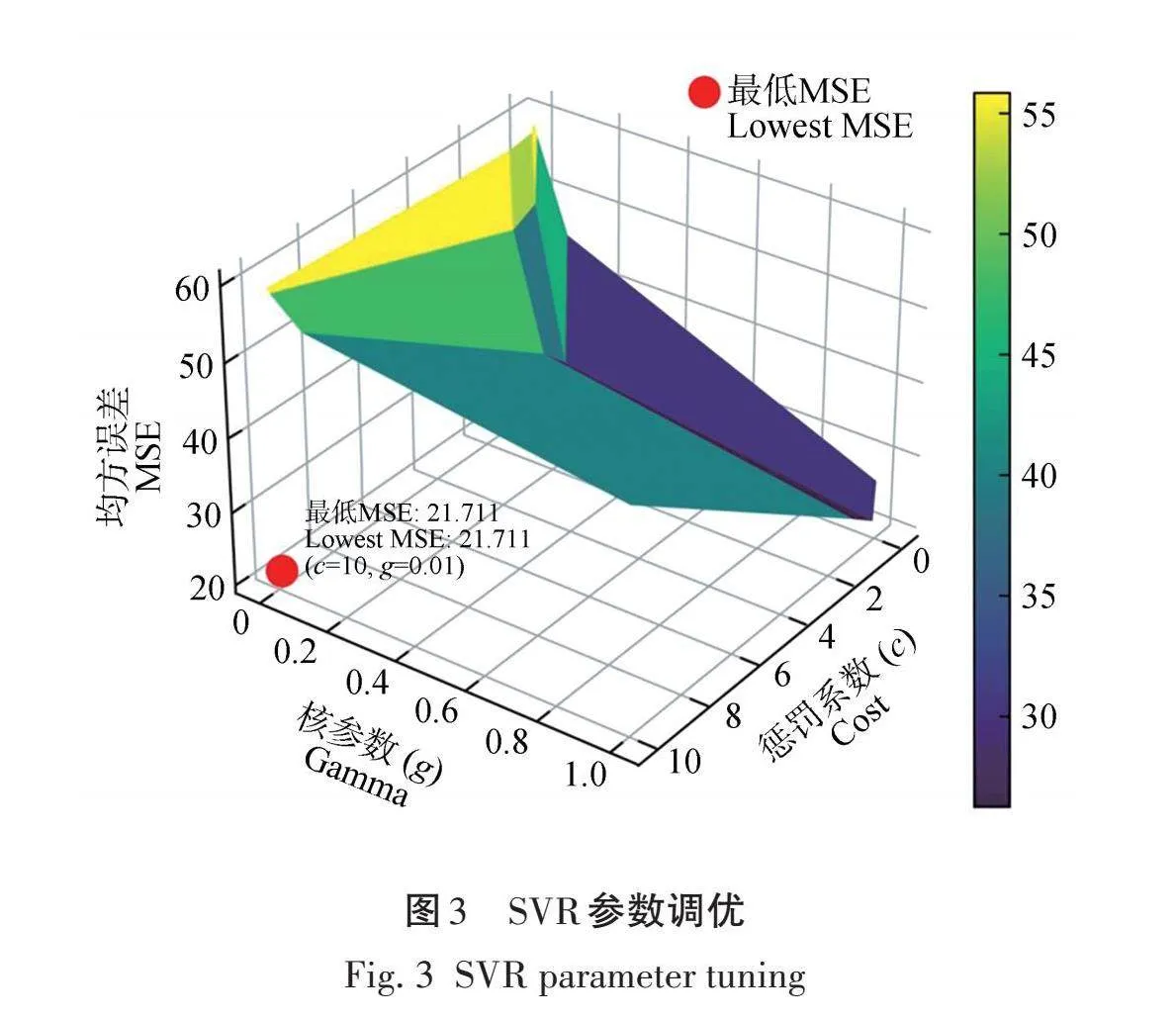
在SVR模型的构建过程中，通过十折交叉验证选择了最优参数组合为c=10和g=0.01，这些参数组合导致了最低的均方误差MSE=21.711，如图3所示。将最优的参数组合代入到模型中，十折交叉验证的结果为R2=0.632、RMSE=4.618 t/hm2、MAE=3.498 t/hm2、MSE=21.416 t/hm2，相较于SMR（R2=0.589）模型拟合精度提高了7.3%。需要注意的是，c=10，表示SVR模型倾向于更严格地拟合训练数据，可以解释模型更复杂，适应噪声更多。但这也意味着该模型对样本数据的泛化性能可能较差。

3.2.3 随机森林模型构建结果

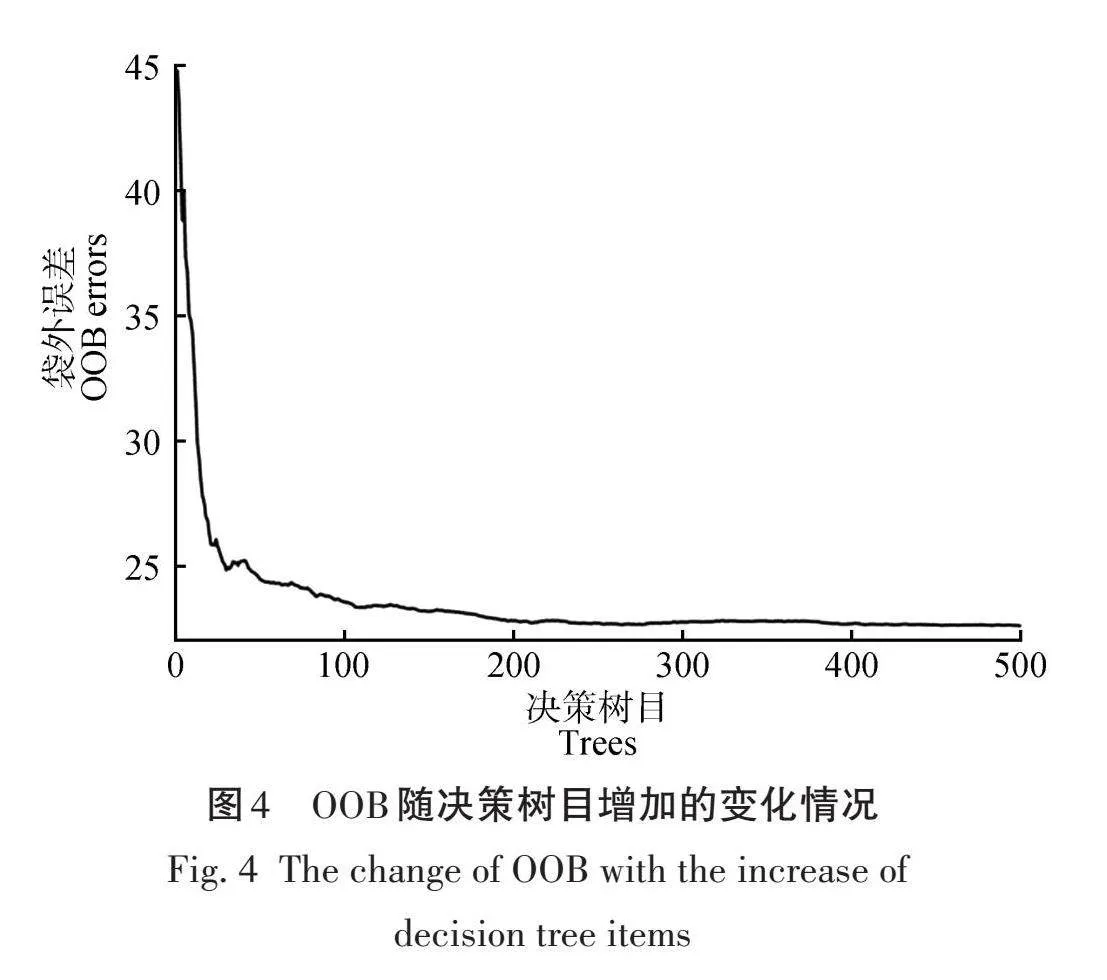
使用R语言中的随机森林包进行装袋法估计，首先确定决策树的数目。将参数中的决策树节点数设置为11（mtry=11），表示在该例中使用全部的特征变量，结果显示，随机森林模型函数默认估计500棵决策树，在每个节点均使用全部的11个变量，根据袋外观测值计算的袋外数据（Out of Band，OOB）为22.71；而准R2=0.659，使用plot画出袋外误差曲线图，如图4所示。由图4可知，随着决策树数目的增加，袋外误差呈现下降趋势，当决策数目大于300时，误差就趋于平稳，这时继续增大决策树数目，也不会使之下降。因此，决策树的数目大于300即可。

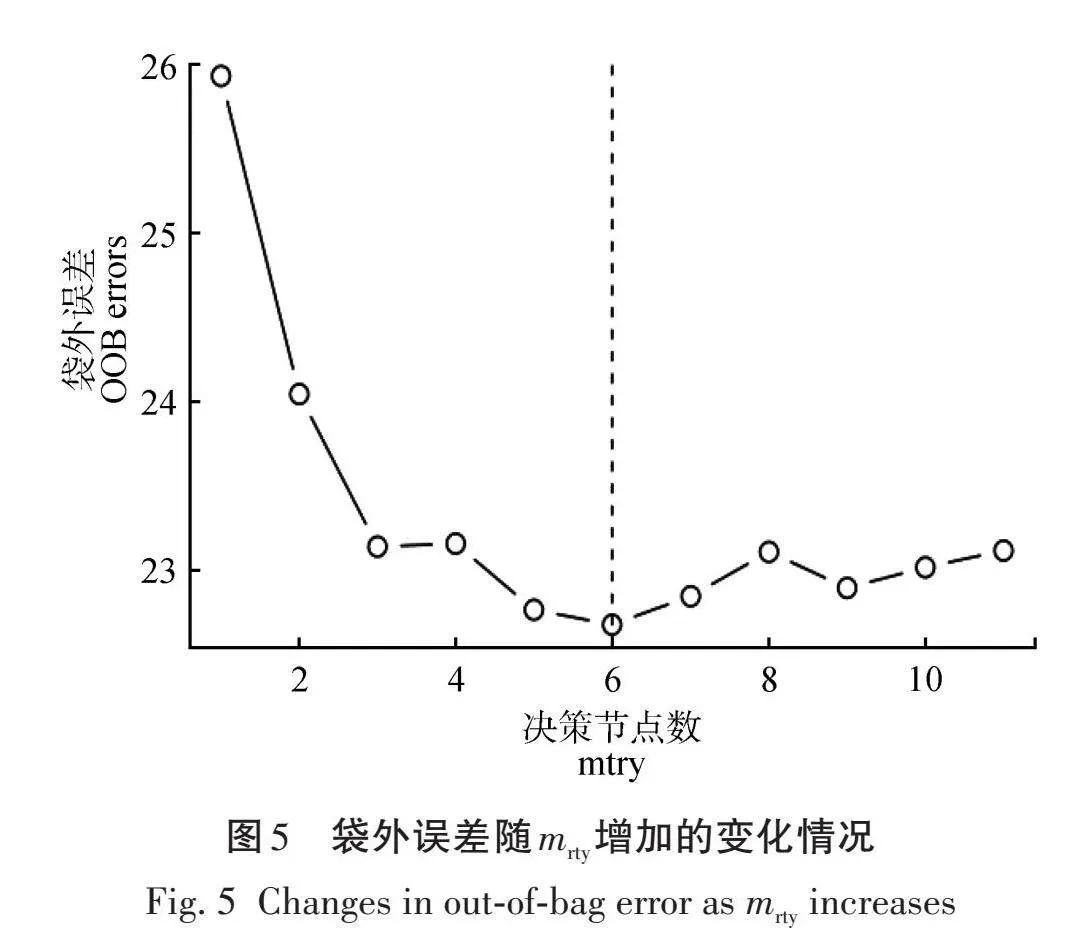
随机森林的另一个重要参数为每次用于节点分裂的变量个数（mtry），这可以通过最小化袋外误差（minMSEOOB）来确定，可用R包随机森林中的tuneRF函数，达到上述的目的，该函数需要设定参 数“step—Factor”表示随机选择变量个数的缩放倍 数，并不考虑mtry的所有可能取值。通过计算寻找 到使袋外误差最小的mtry=6，如图5所示，此时袋外误差为22.735。

将最佳参数（ntree=1 000，mtry=6）带入到随机森林模型当中，得到十折交叉验证的R2=0.661、RMSE=4.435 t/hm2、MAE=3.394 t/hm2、MSE=19.425 t/hm2，表示模型对数据的拟合效果较好，模型的预测较准确。在其模型的构建当中加入了对特征变量的主成分分析，如图6所示，B7在模型的构建当中起主导作用，VARI和TVI的贡献较低。

3.2.4 BP-NN模型构建结果

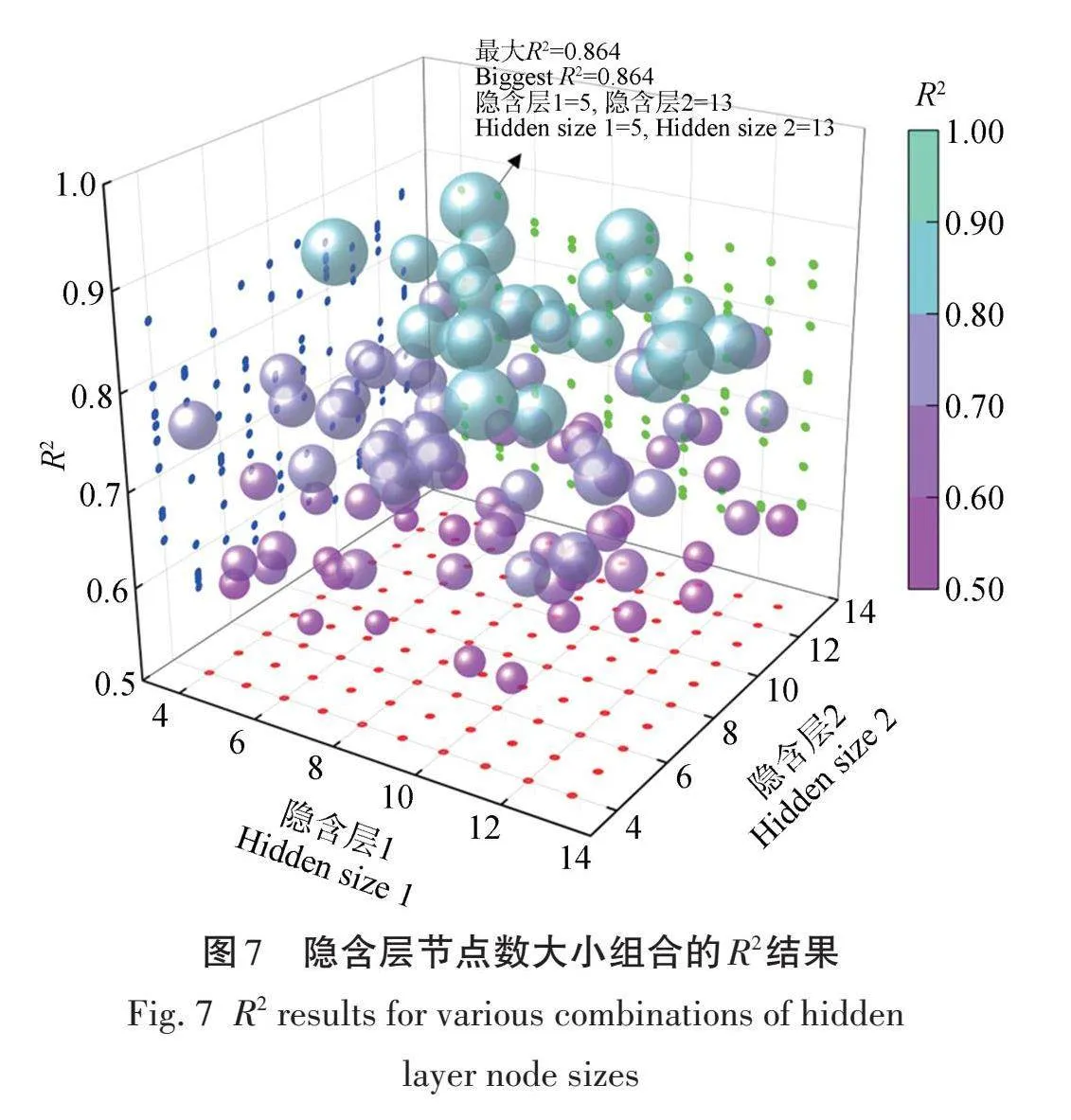
使用Matlab 2020软件创建BP神经网络模型。本研究选择了11个在P<0.01水平上极显著相关的特征因子作为输入层因子，输出层神经元的数量为1，基于经验式（4），得出隐含层中神经元数量的取值范围为4～13。通过嵌套循环来迭代4～13整数的所有可能隐含层节点数大小组合的R2结果，如图7所示。结果显示双隐含层最优的节点数组合为hidden_size1=5，hidden_size2=13，其决定系数R2=0.862，将试验得出最优的参数组合（hidden_size1=5，hidden_size2=13，最大迭代次数=1 000，目标精度=0.001，学习率=0.01）带入到BP神经网络模型中，得到十折交叉验证的R2=0.785，RMSE=3.572 t/hm2，MSE=2.687 t/hm2，MAE=12.757 t/hm2。

3.3 模型评价与检验

3.3.1 模型评价

通过比较4种模型的评估精度和预测效果发 现（表4），SMR模型的拟合效果以及估测能力都 相对较差，SVR、RF和BP-NN模型拟合效果均有提升。BP-NN模型具有最高的R2（0.785）和最小的RMSE（3.572 t/hm2）、MAE（2.687 t/hm2）、MSE（12.757 t/hm2）值，且模型的预测指标均优于其他3种回归模型。因此，BP-NN模型具有最佳的拟合和估测能力，其次是RF、SVR、SMR。

为进一步对模型拟合性能进行可视化分析，分别对4种模型的最佳估测结果绘制散点图如图8所示，分析发现4种模型的预测结果与实测值均表现出较为一致的拟合性，大多数散点在1∶1线附近集中分布；其中BP-NN模型的估测值与实际值更为接近，估测结果更能准确反映研究区森林乔木层生长的实际状况，可作为嘉荫县森林乔木层碳储量的最佳估测模型。

3.3.2 碳储量分段残差分析

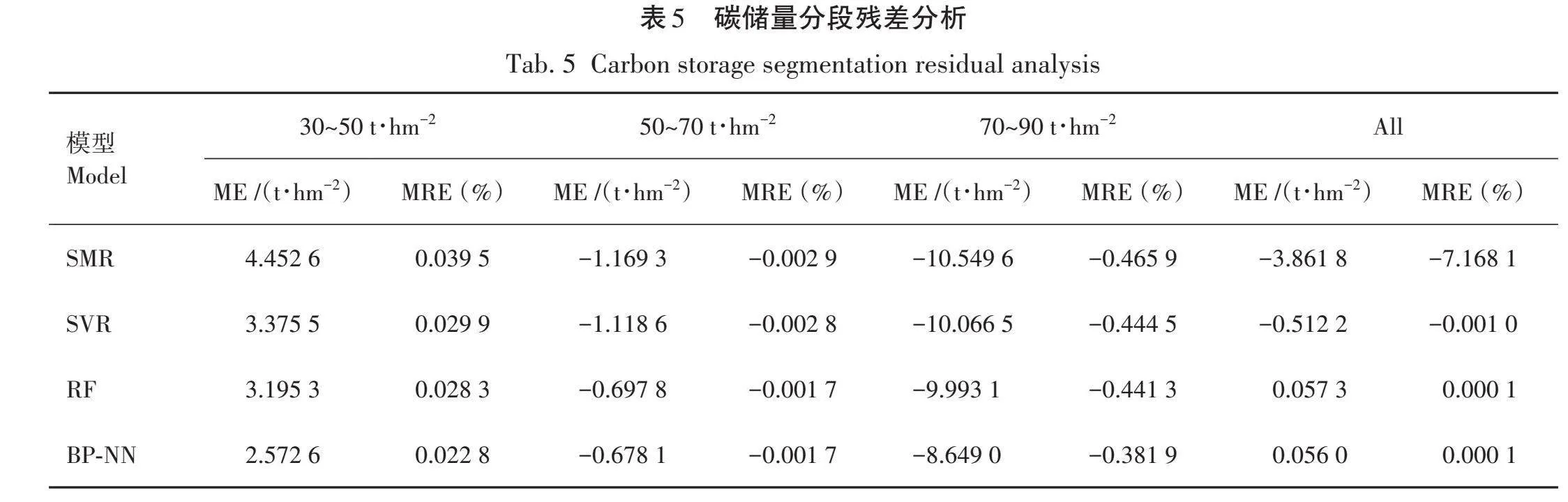
碳储量分段残差结果见表5，由表5可知，与其他3种回归模型相比，BP-NN模型具有较高的估计精度和相对较小的误差；从各碳储量分段看，这4种模型都存在ABGCS高值低估和低值高估的情况 （ME>0，表示高值低估；ME<0，表示低值高估），尤其在70～90 t/hm2分段中，SMR模型表现出最显著的低值高估（ME=-10.549 6，MRE=-0.465 9），且其他3种模型也表现出相对较大的ME、MRE，说明在高碳储量段4种模型的估测能力均显不足，但不能排除此分段样本量较少导致数值较大的因素；在30～50 t/hm2分段中，4种模型均表现出高值低估的情况；在各分段SVR、RF、BP-NN模型的ME和MRE远小于SMR模型，且BP-NN模型的ME和MRE均为最小，因此BP-NN模型具有较好的估测精度。

3.4 森林乔木层碳储量遥感估测光饱和点分析

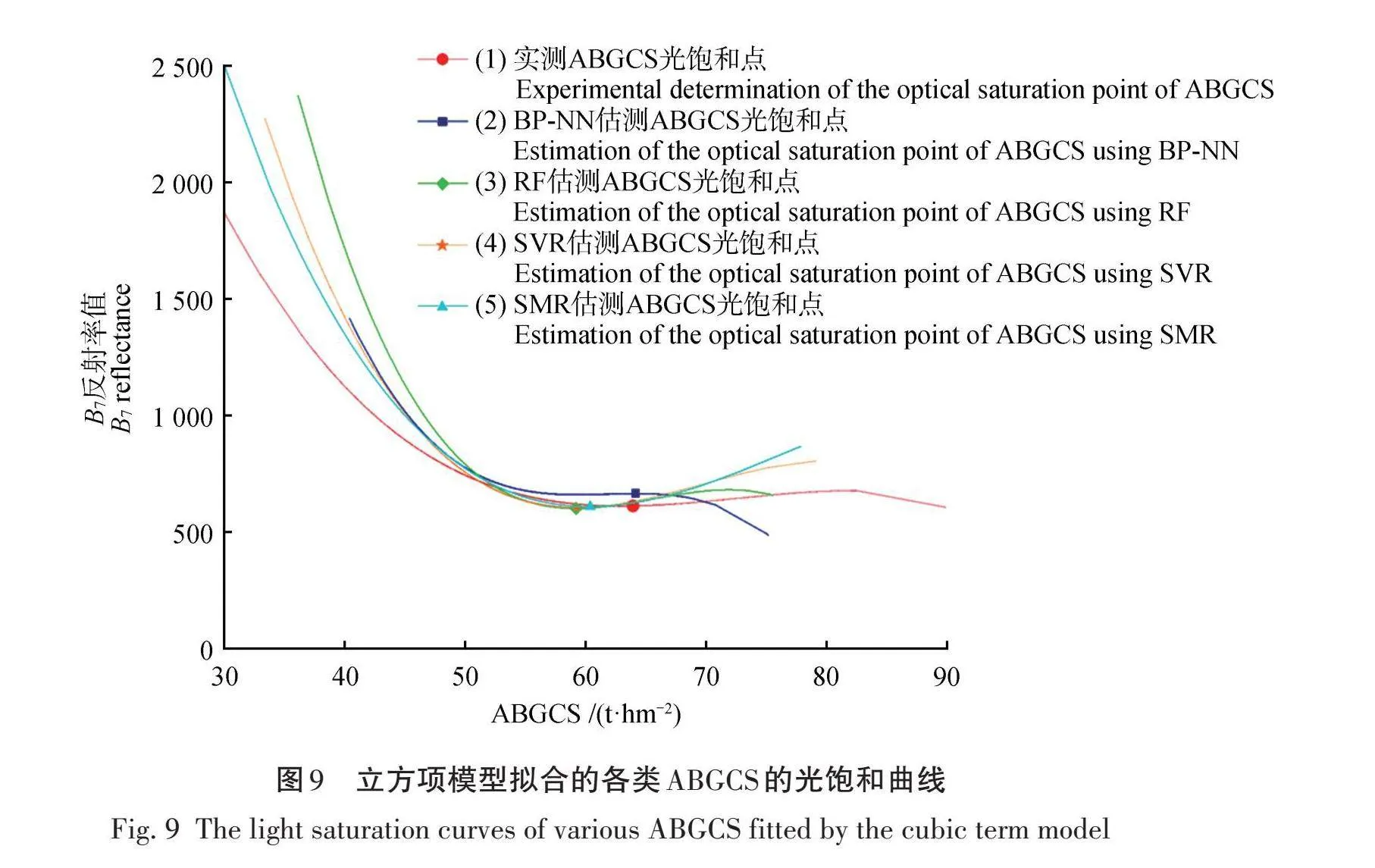
通过选择相关性最高的B7遥感变量，采用二次项和立方项函数拟合嘉荫县森林乔木层碳储量与B7反射率值的函数关系。拟合曲线的拐点对应的自变量值即为嘉荫县ABGCS估测的光饱和值，见表6。由表6可知，相较于二次项模型，立方项模型拟合出较高的R2（0.322），在极小的范围内较好地反映了B7光谱反射率值与ABGCS的关系。因此，以其对应的拐点作为嘉荫县ABGCS光饱和点，其值为63.056 t/hm2。

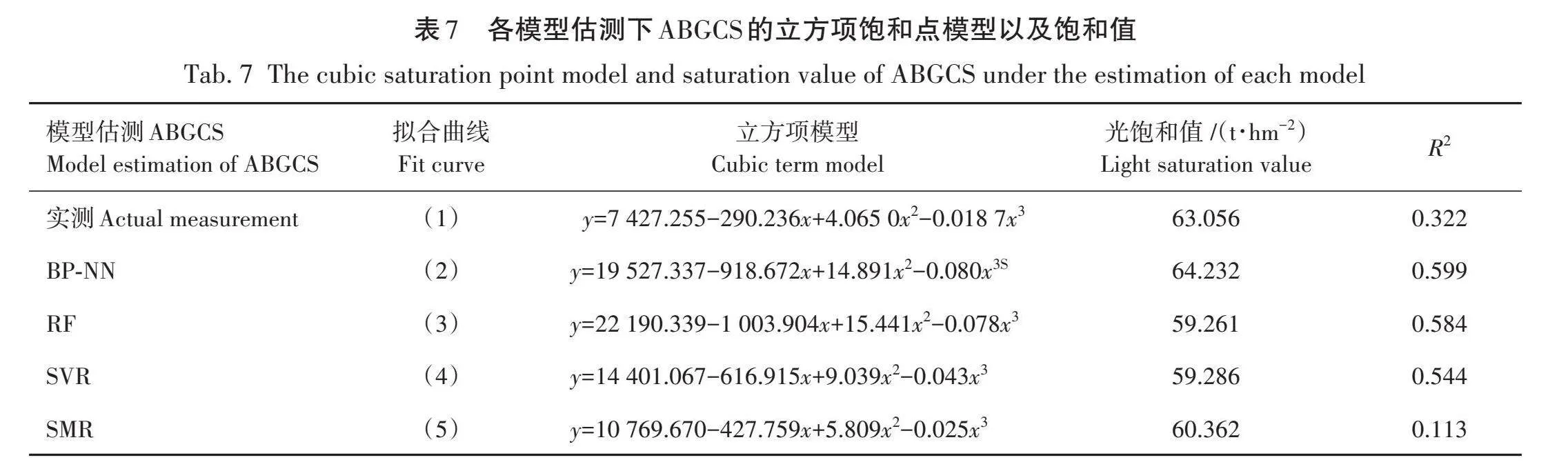
随后采用立方项函数求解4种模型估测的ABGCS与B7反射率值的函数关系，探寻4种模型估测结果的准确性，其立方项函数拟合的各类ABGCS光饱和曲线，如图9所示。结合表7可知，采用B7变量与BP-NN模型估测下的ABGCS进行立方项函数拟合时具有最高的R2（0.599），且估测的饱和值更接近实际饱和值，其值为64.232 t/hm2。进一步验证了BP-NN模型在估测嘉荫县ABGCS具有较为理想的效果。结合上述残差分析结果，在超出实测ABGCS光饱和点的范围内（70～90 t/hm2），4种模型均表现出相对较高的残差，说明光饱和点对遥感估测精度有着较大的限制。

3.5 森林乔木层碳储量反演

为探究伊春市嘉荫县森林乔木层碳储量的空间分布，利用DEM数据以及ArcGIS10.8软件进行坡向的地貌分布图的绘制，如图10所示，将4种模型（SMR、SVR、RF、BP-NN）估计以及实测的嘉荫县森林乔木层碳储量分布图与地貌分布图进行协同分析。结合图10（a）和表8，可以看出研究区域内阳坡面积所占比例最大为30.9%。由图10（b）可以得出，研究区内东南部的碳储量要高于西北部，这一现象的主要原因是由于西北部的年平均气温、降水量、日照时间要低于东南部，导致树木生长缓慢，进而影响碳储量。

位于不同坡向的平均碳储量存在一定差异，具体分布情况见表8。由表8可知，坡向对ABGCS及其空间分配有一定程度的影响。结果显示，不同坡向的森林乔木层碳储量由大到小分布为阳坡、半阳坡、平坡、阴坡、半阴坡。这说明阳坡相较于阴坡、平坡，具有更适合森林生长的光照、水分和温度等条件，使得阳坡的碳储存能力较强。由地理分布引起的地形差异对森林碳储量的空间分布有较大的影响，因此，在生态性建设与保护过程中，应更多关注对阳坡的经营与管护，因地制宜地制定经营管理措施。

4 讨论

4.1 遥感数据选择

自变量的选择对于基于遥感的森林乔木层碳储量估测模型尤为重要，利用逐步回归的方法从80个光谱变量中最终选取了NDVI、TVI、VARI、B4-COR、PCA2、PCA6、PCA10、B7、B9、slope、focalst作为建模变量。为研究森林碳储量的空间分布情况，选择了Landsat系列卫星的影像数据集，这些数据具有较早的记录并持续维护至今。然而，由于大气衰减、低信噪比、有限的年重访次数和相对较低的分辨率，与真实环境存在一定差距［23］，尤其在研究区域从局部扩展到更大范围时，影像质量下降可能导致更大的研究误差。为改进研究，后续观测和研究可以使用分辨率更高的卫星高光谱图像，以研究森林碳储量的空间分布规律。此外，融合多源遥感数据可以实现更好的效果［24］。同时，地面调查数据可以通过地基激光雷达和无人机激光雷达来采集，这不仅可以避免对森林生态系统的破坏，还可以提高观测数据的准确性和便捷性。

4.2 模型对比

在机器学习算法中，SVR模型可处理小样本机器学习问题，并且通过使用核函数来应对非线性问题，将数据映射到高维空间，从而捕捉复杂的关系。然而，需要仔细地超参数调优和数据预处理，以达到最佳性能。而面对较大的数据集时，SVR算法学习效率很低［25-26］；RF模型虽然训练可以高度并行化，能够处理高维度数据，对噪声和离群值相对鲁棒，但当类别不平衡问题严重时，随机森林可能倾向于预测出现频率较高的类别［27］。BP-NN模型具有较强的非线性映射能力和高度自学习自适应能力，也能够并行化处理数据，但也面临着训练时间长、容易过拟合等问题［28］。相较于RF、SVR、SMR构建的模型，BP-NN模型在本次验证过程中具有更高的预测精度和稳定性。机器学习中，样本数量不足会降低模型性能。通过十折交叉验证的结果显示，4种回归模型在不同的交叉验证折叠上表现稳定，说明试验所用的样本数量满足了机器学习算法模型的学习需求。在对SVR模型和BP-NN模型的构建过程中，均采用嵌套循环来迭代参数范围之间所有超参数的大小组合，考虑所有超参数搭配的可能性，进而确定最优的超参数组合，使模型获得最佳性能。其中，3种非参数模型（BP-NN、RF、SVR）相较于参数模型（SMR），拟合精度分别提高了33.3%、12.2%、7.3%，说明非参数模型比参数模型有更好的解释能力，泛化能力更强。

4.3 数据饱和

光谱影像受到多种因素的限制，包括光谱反射率、辐射分辨率以及空间分辨率等。这些限制使得光谱信息对碳储量的敏感度随着碳储量的增大而减小，从而导致数据饱和现象的出现［29］。单位面积碳储量的光饱和情况在许多森林碳储量估测研究中是不可避免的。多项研究已经发现，数据饱和是影响碳储量估测精度的重要原因之一。研究学者们大多以结合不同数据源，利用高光谱影像估测碳储量，以减少碳储量的饱和并提高估测精度［30］。因此，本研究采用了与ABGCS相关性最强的波段（B7），通过立方项模型对Landsat8 OLI影像进行了嘉荫县ABGCS光饱和值的定量研究。

5 结论

本研究中，利用Landsat8 OLI遥感影像及森林资源二类调查数据，选取地学参数及遥感参数能够很好地估测森林乔木层碳储量，为森林碳储量动态监测及研究提供重要数据。本研究通过构建多元逐步回归模型（SMR）、BP神经网络模型（BP-NN）、随机森林模型（RF）、支持向量机回归模型（SVR）对黑龙江省嘉荫县ABGCS估测和空间分布状况的量化研究，利用立方项函数模型估测ABGCS光饱和值，并通过模型预测结果分析立方项模型对ABGCS饱和值的估测能力。

1）通过构建4种回归模型对ABGCS估测以及空间分布分析结果来看BP-NN模型拟合精度最高（R2=0.785，RMSE=3.572 t/hm2，MSE=2.687 t/hm2，MAE=12.757 t/hm2），BP-NN模型能够提供更加准确、稳定的估测结果。

2）采用ABGCS与B7反射率值进行立方项式函数拟合，可用于估算嘉荫县森林乔木层碳储量光饱和点，其值为63.996 t/hm2。采用B7变量与BP-NN模型估测下的ABGCS进行立方项函数拟合时具有最高的R2（0.599），且估测的饱和值更接近实际饱和值，其值为64.232 t/hm2。进一步验证了BP-NN模型在估测嘉荫县ABGCS具有较为理想的效果。

3）BP-NN模型在各ABGCS分段上的ME和MRE均低于RF、SVR和SMR模型。在嘉荫县森林乔木层碳储量空间分布反演中，BP-NN模型的估测范围更为广泛。这有助于在一定程度上解决高值低估和低值高估的问题，进而提高了嘉荫县ABGCS的遥感估测精度和确定阈值的准确性。

【参 考 文 献】

［1］ 郑甲佳，黄松宇，贾昕，等.中国森林生态系统土壤呼吸温度敏感性空间变异特征及影响因素［J］.植物生态学报，2020，44（6）：687-698.

ZHENG J J，HUANG S Y，JIA X，et al.Spatial variation and controlling factors of temperature sensitivity of soil respiration in forest ecosystems across China［J］.Chinese Journal of Plant Ecology，2020，44（6）：687-698.

［2］ BALIMA L H，KOUAME F N，BAYEN P，et al.Influence of climate and forest attributes on aboveground carbon storage in Burkina Faso，West Africa［J］.Environmental Challenges，2021，4：100-123.

［3］ BONAN G B.Forests and climate change：forcings，feedbacks，and the climate benefits of forests［J］.Science，2008，320（5882）：1444-1449.

［4］ 舒洋，郭娇宇，周梅，等.基于IPCC法大兴安岭兴安落叶松人工林碳计量参数研究［J］.温带林业研究，2022，5（1）：30-35，47.

SHU Y，GUO J Y，ZHOU M，et al.Carbon measurement parameters of larch plantation in the Greater Xing′an Mountains based on IPCC method［J］.Research at Temperate Forestry，2022，5（1）：30-35，47.

［5］ 毛学刚，王静文，范文义.基于遥感与地统计的森林生物量时空变异分析［J］.北京林业大学学报，2016，38（2）：10-19.

MAO X G，WANG J W，FAN W Y.Spatiotemporal variation analysis of forest biomass based on remote sensing and ground statistics［J］.Journal of Beijing Forestry University，2016，38（2）：10-19.

［6］ 穆喜云.森林地上生物量遥感估测方法研究［D］.呼和浩特：内蒙古农业大学，2015.

MU X Y.Research on the remote sensing estimation method of forest aboveground biomass［D］.Hohhot：Inner Mongolia Agricultural University，2015.

［7］ 李德仁，王长委，胡月明，等.遥感技术估算森林生物量的研究进展［J］.武汉大学学报·信息科学版，2012，37（6）：631-635.

LI D R，WANG C W，HU Y M，et al.General review on remote sensing-based biomass estimation［J］.Geomatics and Information Science of Wuhan University，2012，37（6）：631-635.

［8］ OU G L，LV Y Y，XU H，et al.Improving forest aboveground biomass estimation of pinus densata forest in Yunnan of southwest China by spatial regression using Landsat 8 images［J］.Remote Sensing，2019，11（23）：2750.

［9］ CHEN Q，MCROBERTS R E，WANG C，et al.Forest aboveground biomass mapping and estimation across multiple spatial scales using model-based inference［J］.Remote Sensing of Environment，2016，184：350-360.

［10］ ZHAO P P，LU D S，WANG G X，et al.Examining spec-tral reflectance saturation in landsat imagery and corresponding solutions to improve forest aboveground biomass estimation［J］.Remote Sensing，2016，8（6）：469.

［11］ FANG J Y，CHEN A P，PENG C H，et al.Changes in forest biomass carbon storage in China between 1949 and 1998［J］.Science，2001，292（5525）：2320-2322.

［12］ ZHANG C H，JU W M，CHEN J M，et al.China′s forest biomass carbon sink based on seven inventories from 1973 to 2008［J］.Climatic Change，2013，118（3/4）：933-948.

［13］ 肖兴威.中国森林资源清查［M］.北京：中国林业出版社，2005.

XIAO X W.Forest resources inventory in China［M］.Beijing：China Forestry Press，2005.

［14］ TUIA D，VERRELST J，ALANSO L，et al.Multioutput support vector regression for remote sensing biophysical parameter estimation［J］.IEEE Geoscience and Remote Sensing Letters，2011，8（4）：804-808.

［15］ ZHAO Y，WANG K.Fast cross validation for regularized extreme learning machine［J］.Journal of Systems Engineering and Electronics，2014，25（5）：895-900.

［16］ DONG L J，LI X B，PENG K.Prediction of rockburst classification using random forest［J］.Transaction of Nonferrous Metals Society of China，2013，23（2）：472-477.

［17］ 林成德，彭国兰.随机森林在企业信用评估指标体系确定中的应用［J］.厦门大学学报（自然科学版），2007，46（2）：199-203.

LIN C D，PENG G L.Application of random forest on selecting evaluation index system for enterprise credit assessment［J］.Journal of Xiamen University：Natural Science Edition，2007，46（2）：199-203.

［18］ 李萍，曾令可，税安泽，等.基于MATLAB的BP神经网络预测系统的设计［J］.计算机应用与软件，2008，25（4）：149-150.

LI P，ZENG L K，SHUI A Z，et al.Design of the BP neural network prediction system based on MATLAB［J］.Computer Applications and Software，2008，25（4）：149-150.

［19］ 沈花玉，王兆霞，高成耀，等.BP神经网络隐含层单元数的确定［J］.天津理工大学学报，2008，24（5）：13-15.

SHEN H Y，WANG Z X，GAO C Y，et al.Determining the number of BP neural network hidden layer units［J］.Journal of Tianjin University of Technology，2008，24（5）：13-15.

［20］ 李振，陈香香，杨文府.BP人工神经网络算法的探究及其应用［J］.数字技术与应用，2016（2）：132-132.

LI Z，CHEN X X，YANG W F.BP artificial neural network algorithm exploration and its application［J］.Digital Technology and Application，2016（2）：132-132.

［21］ 赵盼盼.基于Landsat TM和ALOS PALSAR数据的森林地上生物量估测研究［D］.杭州：浙江农林大学，2016.

ZHAO P P.Forest aboveground biomass estimation study based on Landsat TM and ALOS PALSAR data［D］.Hangzhou：Zhejiang A & F University，2016.

［22］ 孙雪莲.基于Landsat 8-OLI的香格里拉高山松林生物量遥感估测模型研究［D］.昆明：西南林业大学，2016.

SUN X L.A remote sensing estimation model of Alpine pine forest based on Landsat8-OLI［D］.Kunming：Southwest Forestry University，2016.

［23］ ZHANG X，JIA W，SUN Y，et al.Simulation of spatial and temporal distribution of forest carbon stocks in long time series-based on remote sensing and deep learning［J］.Forests，2023，14（3）：483.

［24］ 王飞平，张加龙.基于碳卫星的森林碳储量估测研究综述［J］.世界林业研究，2022，35（6）：30-35.

WANG F P，ZHANG J L.Review of forest carbon reserve estimation study based on carbon satellite［J］.World Forestry Research，2022，35（6）：30-35.

［25］ DONG L H，ZHANG L J，LI F R.Developing two additive biomass equations for three coniferous plantation species in northeast China［J］.Forests，2016，7（7）：136.

［26］ 李紫荆，刘彦枫，冉娇，等.基于Landsat 8 OLI的云南元江流域森林生物量光学遥感估测及其饱和点分析［J］.西南林业大学学报（自然科学），2023，43（1）：126-136.

LI Z J，LIU Y F，RAN J，et al.Optical remote sensing estimation and saturation point analysis of forest biomass in Yuanjiang Basin，Yunnan Province Based on Landsat 8 OLI［J］.Journal of Southwest Forestry University：Natural Science，2023，43（1）：126-136.

［27］ 田惠玲，朱建华，何潇，等.基于随机森林模型的东北三省乔木林生物质碳储量预测［J］.林业科学，2022，58（4）：40-50.

TIAN H L，ZHU J H，HE X，et al.Prediction biomass carbon stock of arbor forest of three provinces in northeastern China based on random forest model［J］.Scientia Silvae Sinicae，2022，58（4）：40-50.

［28］ 范文义，张海玉，于颖，等.三种森林生物量估测模型的比较分析［J］.植物生态学报，2011，35（4）：402-410.

FAN W Y，ZHANG H Y，YU Y，et al.Comparison of three models of forest biomass estimation［J］.Journal of Plant Ecology，2011，35（4）：402-410.

［29］ WANG G X，ZHANG M Z，GERTNER G Z，et al.Uncertainties of mapping aboveground forest carbon due to plot locations using national forest inventory plot and remotely sensed data［J］.Scandinavian Journal of Forest Research，2011，26（4）：360-373.

［30］ FLEMING A L，WANG G X，MCROBERTS R E.Comparison of methods toward multi-scale forest carbon mapping and spatial uncertainty analysis：combining national forest inventory plot data and landsat TM images［J］.European Journal of Forest Research，2015，134（1）：125-137.