例谈逻辑思维的培养策略

几何证明题是初中数学的一种基础题型，更是一门展现学生思维的艺术。尽管一些人认为垂直、平行等几何概念与现实生活脱节，但实则不然。学生可以在几何证明题中掌握数学符号和基础知识，更能在证明过程中深度锤炼逻辑思维，增强发散性思维。当学生能熟练解答几何证明题，灵活运用所学，尤其是以多元视角解答同一问题时，其逻辑思维能力已处于较高水平，这种能力将自然体现于他们日常的生活决策与问题解决过程中。因而在教学实践中，教师应积极强化学生的逻辑思维训练，提升他们思维的灵活性，注重培养他们运用基础知识与技能解决实际问题的能力，从根本上增强学生的逻辑思维能力。笔者认为，通过几何证明题来培养学生的思维能力时，要注意以下几个方面。

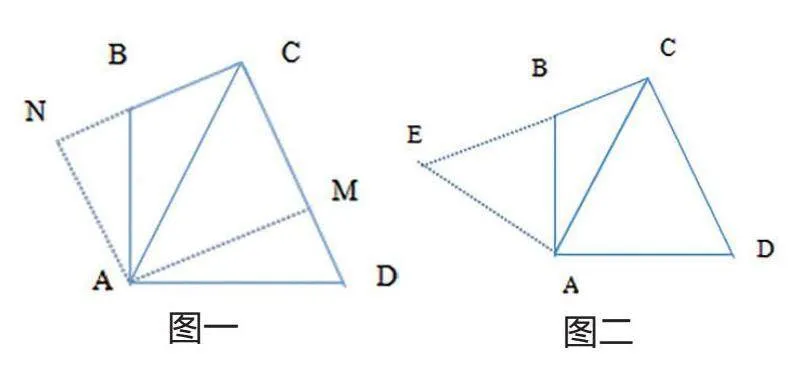
精选典型例题，创设问题情境，强化综合分析能力。问题是数学探索的起点，精选例题能激发学生兴趣，促使其主动思考。以七年级几何题为例，四边形ABCD中，条件为AB=AD， AB⊥AD，DC⊥BC， AC=6，求其面积。带领学生分析此题得出，关键在于将不规则四边形转化为规则图形。利用已知条件AB=AD，AB⊥AD， DC⊥BC，引导学生思考如何作辅助线。讨论后，指导学生过A点作BC、CD的垂线，形成正方形CNAM（如图一），进而通过证明△ABN与△ADM全等来求解面积。但对七年级学生而言，求对角线为6的正方形面积仍有较大难度，可启发他们继续转为求三角形面积（如图二），由A点出发作AC垂线，交CB延长线于点E，转化为等腰直角△EAC求解。此过程不仅能使学生巩固新知、复习旧识，还能促进他们逻辑思维与问题解决能力的发展，同时活跃课堂氛围，让学生享受思考的乐趣。

给予学生充分的思考时间，以培养其独立思考与逻辑思维能力。部分教师担心课堂时间有限，认为减少讲解时长会影响知识传授，实则不然。诚然，细致讲解或能即时见效，但学生自主思考所得的价值或许更高。如教授“旋转”的知识后，有这样一道题：点D在等边△ABC外，∠ADC=30°，AD=4，CD=3，求BD。此题初看有难度，但熟悉旋转题型的学生大多能独立思考并顺利解决。在教学中，笔者先讲解类似例题，随后将此题留给学生自行探索。经过约20分钟思考，几位学生终于成功解题，他们一个个面带微笑，眼神中闪烁着成就感。课上，他们分享了自己的思考，更多学生由此掌握了解题思路。一年过去，仍有学生在提及此题时感慨，这样的独立思考经历让他们得以享受思维的乐趣，增强了学习几何的信心与兴趣。

适时引导，激发学生的发散逻辑思维。教师的引导应聚焦于学生产生困惑之时，既非全盘提示，亦非放任自流。在解几何题时，首要任务是明确已知与所求，要引导学生从已知推向未知，当逻辑链条清晰时，问题自然就能解决。以一道矩形知识的复习题为例：矩形ABCD中，已知AB、AD长度及对角线交点O，P为AD上动点，PE、PF分别垂直AC、BD，求PE+PF之和。若学生讨论后仍无头绪，可启发其思考P点位置对PE+PF值无影响，故可取特殊点（如A或D）简化问题，转化为求直角三角形斜边上的高，从而得出答案。但需强调，上述方法只是帮助学生打开解题思路，一般更适用于选择、填空等不需要考查解题过程的题目，需根据题型灵活使用。进一步，引导学生探索P点不特殊时的解法。在学生的充分思考与讨论之后，可提示他们使用面积法：连接OP，利用三角形面积关系求解题目。同时，鼓励学生运用相似三角形知识，通过构建比例关系求解，拓宽解题思路。整个过程中，教师应密切关注学生的参与度，鼓励积极思维，通过一题多解的训练，增强学生思维的灵活性。备课时，应深入挖掘教材，构建知识网络，设计难度递进的题目，促进学生思维广度与深度的发展。

总之，答几何证明题犹如侦破案件，学生能在推理演绎中提升思维能力。部分教师应摒弃“几何知识无用”的偏见，积极拓展学生思维疆域，激发其主动思考，达成培养他们思维品质的目标。