利用集成剪枝和多目标优化算法的随机森林可解释增强模型

摘 要：随机森林模型是广泛应用于各个领域的经典黑盒模型，而黑盒模型的结构特征导致模型可解释性弱，需要借助可解释技术优化随机森林的可解释性，从而促进其在可靠性要求较高场景的应用与发展。研究构建了基于集成剪枝和多目标优化算法的规则提取模型，集成剪枝在解决树模型规则提取易陷入局部最优的问题上具有代表性，多目标优化在解决规则准确性和可解释性的平衡问题上有多个领域的应用。模型验证结果表明，所构建模型能够在不降低准确性的前提下优化模型的可解释性。本研究首次将集成剪枝技术与多目标优化算法相融合，增强了随机森林的可解释性，有助于推动该模型在可解释性要求较高领域的决策应用。

关键词：随机森林；可解释增强；集成剪枝；规则提取；多目标优化算法

中图分类号：TP391 文献标志码：A 文章编号：1001-3695（2024）10-010-2947-08

doi：10.19734/j.issn.1001-3695.2024.02.0047

Interpretability enhancement model of random forest using ensemble pruning and multi-objective evolutionary algorithm

Li Yang1， Liao Mengjie1， 2， Zhang Jian1， 2

（1.School of Economics & Management， Beijing Information S&T University， Beijing 100192， China; 2.Beijing Key Laboratory of Big Data Decision-making for Green Development， Beijing 100192， China）

Abstract：Random forest is a classic black-box model that is widely used in various fields. The structural characteristics of black-box models lead to weak model interpretability， which can be optimized with the help of interpretable techniques to promote the application and development of random forest in scenarios with high reliability requirements. This paper constructed a rule extraction model based on ensemble pruning and multi-objective evolutionary algorithm. Ensemble pruning is an effective method for solving the problem of extracting rules from tree models that tend to fall into local optima， and multi-objective evolutionary has several applications in balancing rule accuracy and interpretability. This paper found that it improved interpreta-bility without sacrificing accuracy. This study integrated ensemble pruning technique with a multi-objective evolutionary algorithm， which enhances the interpretability of random forests and helps promote the decision-making application of this model in areas with high interpretability requirements.

Key words：random forest; interpretability enhancement; ensemble pruning; rule extraction; multi-objective evolutionary algorithm

0 引言

人工智能是引领新时代产业革命和科技进步的重要驱动力，对人工智能可解释性的要求同样备受关注。2021年9月25日，我国国家新一代人工智能治理专业委员会发布的《新一代人工智能伦理规范》第12条规定，要在算法设计、实现、应用等环节，提升透明性、可解释性、可理解性；欧盟的《通用数据保护条例》（GDPR）提出了“解释权”的概念，即由算法作出的决定对用户产生影响，那么用户有权知晓这些决定的具体解释［1，2］。在管理决策领域，机器学习模型以其面向复杂场景的高精确度等优势广泛应用，但针对某些对模型存在透明度要求的行业，其黑盒模型结构特征制约了其发展，如医疗诊断、信用贷款风险评估、推荐系统等领域。而准确性与可解释性这两个特点往往难以在同一模型当中同时被满足，因此，如何提升准确性较高的黑盒模型的可解释性成为了近年来的研究热点［3］。而在管理决策领域，如何在不降低模型准确性的同时提升其可解释性，可以大大提升模型的可信度，对管理决策领域具有极为重要的现实意义。

可解释技术（explainable artificial intelligence， XAI）为机器学习模型的可解释性优化提供了可行方案，可为决策者提供文本化或可视化的解释模型［4］。其中有两种典型技术路线，其一为全局可解释，即从黑盒模型中训练一个结构透明的模型并对源模型进行替代；其二为局部可解释，旨在为个例预测结果提供解释，并分析关键因素对模型结果的影响，代表方法为SHAP、LIME［5，6］。其中，随机森林集成多棵决策树是对样本进行训练并预测的一种集成学习方法，在风险评价领域效果良好且具有较强的鲁棒性，特别是针对小规模结构化数据的评价问题表现出优于深度学习的性能［7］。而由于随机森林生成了大量的基决策树，且基决策树的推理逻辑不统一导致其独立的基决策树不具备解释价值，所以随机森林仍然被认为是一种不具备良好解释性的黑盒模型，限制了其面向可解释性要求高场景的应用范围［8］。

近年来，有学者从不同角度对随机森林模型的可解释优化进行研究。一类是使用构建单一决策树的方法将随机森林转变为可解释模型，并保持了原模型的准确性。文献［9］先提供了构建基于森林的树（forest-based tree，FBT）的方法，通过对模型的修剪和规则的合取操作，将源模型转换为一棵决策树。该方法在保持树模型性能的基础上为决策者解释了模型预测的过程。FBT方法忽略了每条规则的可解释性，为决策者的理解增加难度［10］。另一类是直接从集成树中提取规则。这类方法将树模型转换为大量的规则集，再使用贪婪或启发式算法从中寻找具有价值的规则子集。如Boruah等人［11］通过减少决策树提取的规则数量来提高决策支持系统的可理解性。该方法能够提取出最直接的规则供决策者理解模型，而挑战在于从庞大的解空间中找到性能最优的规则子集，避免搜寻算法陷入局部最优。

综上所述，将随机森林转换为规则集是随机森林可解释性增强的重要路径之一，而实现该转换主要面临两大问题：一是提取规则因数量过大而容易陷入局部最优，二是提取规则在准确性和可解释性上难以兼得。集成剪枝是解决输出容易陷入局部最优问题最具代表性的方法，其优势在于在保证随机森林性能不变或提升的基础上减小集成树的规模；而多目标优化对于提取规则的准确性和可解释性上的平衡问题在信用风险评估、医学检测等多个领域效果显著。因此，为更好地解决规则模型存在的问题，本研究将集成剪枝与多目标优化算法的优势相结合，利用集成剪枝减少随机森林中基树的数量，在提升随机森林模型性能的同时通过减小初始规则数量的方式提升模型搜索最优解的能力，再使用多目标优化算法得到准确性和可解释性均衡的优化规则集，最终实现随机森林的可解释性增强。

基于此，本研究建立基于剪枝随机森林的规则提取模型（pruned random forest-based rule extraction，PRFRE），提高提取优化规则集的稳定性，提供准确性和可解释性均优的决策规则集。该模型首先修剪训练好的随机森林模型，减少模型中决策树的数量，简化随机森林的复杂性。在集成剪枝方法的选择上，本研究列举各类分类器技术，并不影响后续规则的性能。随后，构建规则的准确性和可解释性指标，进行基于单个指标的候选规则集选择，进一步减少规则数量。最后，使用基于多目标优化算法（multi-objective evolutionary algorithm，MOEA），以规则的准确性和规则的可解释性为两个优化目标对候选规则集进行多轮迭代优化，最终得到优化规则集。本文首次将集成剪枝与多目标优化算法相融合，实现模型可解释性增强，且优化规则集可供决策者对原模型进行理解，或直接代替原模型进行智能决策。

1 相关研究综述

1.1 机器学习的可解释性研究

由于机器学习模型的预测性能与可解释性的互斥关系，机器学习模型的可解释性研究应运而生。可解释性通常与可理解性同时出现，两个用语的含义并不完全一致，区别在于可理解性在于原模型可直接为人类所理解，而可解释性是指构造新的透明模型作为人类与复杂机器学习模型的桥梁供人类理解［12］。文献［3］综合不同研究对可解释性的描述，将对机器学习模型的可解释性定义为使用清晰、简单的方式对不同背景的用户进行模型进行智能决策解释的方法。研究机器学习模型可解释性的意义不仅是为了帮助人类相信和理解复杂黑盒模型的决策机制，也是解决机器学习模型运用于各领域存在伦理问题的必然要求。目前许多机器学习模型会受到隐蔽的攻击，存在对不具有代表性群体的偏见和隐私泄露的情况，导致用户对所有机器学习模型可信度的降低［13］。

学界提出了不同的技术来应对提高机器学习模型可解释性的挑战。这些技术可以分为局部可解释技术和全局可解释技术。前一种技术旨在为个体预测提供易于理解的解释，而不必将模型机制解释为一个整体。经典的局部可解释技术是 LIME 和 SHAP，是以样本个体为研究对象预测学习可解释的局部模型。目前，如文献［14，15］所述，SHAP已应用于医疗诊断、信用贷款、情报挖掘等多个学科的可解释性研究中。全局可解释性是通过从给定的不透明模型生成可解释模型来实现的。在全局可解释性研究中，决策树、决策规则、最近邻模型和线性模型常被用作可解释模型的基础［5］。随机森林模型的可解释性属于全局可解释性研究，即通过对随机森林模型的处理形成新的透明模型来获得可解释性，具体介绍将在下一节展示。

1.2 随机森林的可解释性研究

近些年对于随机森林的可解释性研究，除通用的局部解释和可视化方法以外，主要分为集成剪枝和规则提取两种方法［8］。集成剪枝是指将随机森林模型的基决策树数量进行缩减以获取优秀的最小森林的方法。剪枝的目的在于在保持或提高原有随机森林模型精度的基础上，减小模型复杂度的同时带来存储空间和分类时间上的节省。此方法的前提是文献［16］发现集成树模型生成了大量的决策树，其中有许多树仅存在几个节点的不同，且空间划分的方式高度相似。该研究结果为随机森林剪枝方法提供了理论依据。目前已经提出的有效剪枝技术，主要分为基于优化的搜索、贪婪搜索、基于聚类的搜索和基于排序的搜索［17］。以上基于搜索的剪枝方法需要定义指标用于该指标的最大化或最小化子集。Mohammed等人［18］的研究提出了各类度量方式来排列随机集成剪枝器并证明了指标的稳定性和可靠性。然而，由于集成剪枝并没有对基决策树的内部结构进行加工，该方法更多被用于黑盒模型向透明模型转换的过渡步骤［7］。

基于规则提取的随机森林可解释性研究旨在通过提取从决策树根节点到叶节点的决策路径，生成规则集来提供模型全局解释能力。但由于原模型提取的规则数量众多且性能参差不齐，所以需要对规则进行额外的筛选操作。Mashayekhi等人［19］提出了一种RF+HC的规则提取方法，该方法从随机森林中用爬坡法寻找规则集，从而减少规则的数量并提高可理解性，该方法在UCI乳腺癌数据集上进行了评估。文献［20］为探究杰出学者对知识创新绩效的影响，构建三类学者群组并使用CART算法进行规则提取，发现潜在的决策规则。Wang等人［21］提出了一种基于堆积的前列腺癌诊断的可解释的选择性集合学习方法，并从树状集合中挖掘了诊断规则，同时考虑了准确性和可解释性，然而该文并没有对挖掘的规则进行优化。学者们通过教学法、启发式算法等多种思路在保证规则集相对于复杂模型保真度的同时也提高了可解释性，但由于初始规则数量太多，搜索优化规则集的结果存在不稳定的情况。

综上所述，规则提取方法在随机森林的可解释性研究中已取得一些进展，但从初始规则集到优化规则集的搜索方法仍有进一步优化空间。基于此，本研究将集成剪枝方法融入规则提取中，构建基于剪枝随机森林的规则提取模型，减小初始规则集的规模，提升输出规则集的准确性和可解释性。

2 模型构建方法

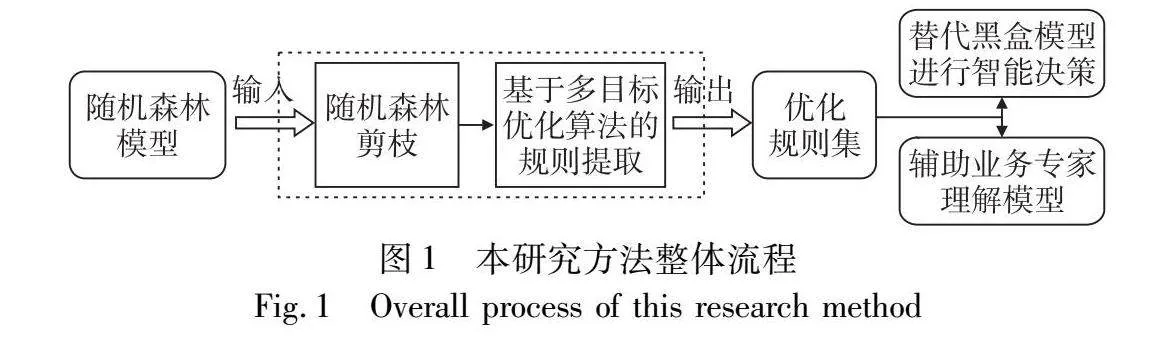
本章围绕具备黑盒模型的全局可解释性转换，构建了PRFRE模型，用于解释随机森林模型进行预测的逻辑。该模型包含两个阶段，第一阶段是随机森林剪枝，第二阶段是基于多目标优化的规则提取。PRFRE模型的算法流程如算法1所示。该模型主要包含两个部分，首先是随机森林剪枝，以及基于多目标优化的规则提取。图1为本研究方法的整体流程，该图清晰地显示了PRFRE模型从输入到输出的流程，经过预处理的数据输入至随机森林中进行训练。首先进行随机森林剪枝，对剪枝后的随机森林进行基于多目标优化算法的规则提取，包括基于单指标的规则筛选流程，最终得到优化规则集。在接下来的内容中，将对模型中的各个细节作详细介绍。

算法1 基于剪枝随机森林的规则提取（PRFRE）模型

输入：训练数据D，剪枝技术F，设置相关参数，即单棵决策树的最大深度、树的个数、初始种群的个数、初始激活元素个数、交叉概率、变异概率、进化次数。

输出：优化规则集Rule_opt。

1 使用训练数据D训练随机森林 Tree_rf

2 Tree_prf ← prune（F， Tree_rf） //对随机森林进行剪枝

3 Rule_inital ← Tree_prf//从剪枝随机森林中抽取规则

4 Rule_cand ← //创建候选规则集

5 for each rule in Rule_inital do

6 Rule_aim ← rule pre selection（Rule_inital， D） /*选取候选规则集*/

7 Rule_cand ← Rule_cand ∪ Rule_aim

8 end for

9 Rule_opt ← MOEA-based rule selection（Rule_cand， D） /*基于多目标优化的规则提取*/

2.1 随机森林剪枝

随机森林模型在训练中生成了大量的基决策树，这些决策树相互独立且性能参差不齐，一些性能较差的基决策树会影响对随机森林模型的解释。随机森林模型剪枝是通过提取部分模型中的基决策树，达到保持或提高集成树模型性能的同时减少模型复杂度的效果，提高下一步规则挖掘结果的表现。基于贪婪算法的修剪方法和基于排序的修剪方法是目前公认的探寻最优修剪效果的便捷方法［18］。首先是使用贪婪算法进行修剪，即指定性能指标（如AUC、ROC），以迭代形式将基决策树置于初始为空集的优化集合中，直至没有基决策树可提高优化集合的性能，最终得到的优化集合视为修剪后的输出。此类方法相较于其他方法拥有较少的超参数配置和较好的修剪效果，但容易出现局部最优。基于排序的修剪方法是先将基决策树按照某种规律进行排序，再根据排序结果进行启发式修剪。基于排序的修剪被证实具有效能和灵活性两个优势，即得到的子集最接近最优解，并且可以轻松调整排序策略来适应存储和计算上的限制［22～24］。本研究选取四种不同的修剪方法并设计实验评估性能，分别为DISC、MRMR、MDEP和AUC-贪婪方法。下面将对这些方法作详细介绍。

2.1.1 判别分类器剪枝

判别分类器剪枝（discriminant classifiers pruning， DISC）由Cao等人［22］于2018年提出。该方法提出两个假设来优化当前的基分类器Su－1：

假设1 对于被Su－1正确分类的样本，一个好的候选分类器应该对尽可能多的这样的样本作出同样的决定。

假设2 对于被Su－1错误分类的样本，一个好的候选分类器应该尽可能多地正确分类这些样本。

第一个假设将候选分类器与合成集成联系起来，而第二个假设表示候选分类器如何与目标相关。该方法集中于寻找最具判别性的分类器，该分类器相对于Su－1和Y。样本被分为两部分，{mis}表示Su－1错误分类的样本集合，{cor}表示Su－1正确分类的样本集合，合并后的分类器选择公式如下：

su=argmaxk［I（ψmisk;Ymis）+1u－1∑ψi∈Sn－1I（ψcork;ψcori）］（1）

其中：k∈Lu－1且Su=Su－1∪{Su}。第一项I（ψmisk;Ymis）是ψk根据Su－1的错误标记样本从真标签Y获得的互信息；第二项1u－1∑ψi∈Sn－1I（ψcork;ψcori）是ψk从Su－1的所有成员获得的与正确分类样本相关的平均互信息。

2.1.2 最大相关性和最小冗余度剪枝

最大相关性和最小冗余剪枝（maximum relevance & minimum redundancy pruning， MRMR）同样由Cao等人［22］于2018年提出。该算法的思路起源于用于减少特征选择问题中冗余的流行算法mRMR。该剪枝方法涉及两种关系：一种是候选类和组件类之间的关系，另一个是候选类和目标类之间的关系。候选类别表示要包括的第k个分类器的类别标签输出，而组件类别表示复合集成的类别标签输出。在剪枝集Dpr上估计得到的具有最高精准度的分类器被存储在S1中，作为待扩展的初始子集。下一个待识别的第k个分类器Su会根据以下公式选择：

su=argmaxk［I（ψk;Y）－1u－1∑ψi∈Su－1I（ψk;ψi）］（2）

其中：k∈Lu－1且Su=Su－1∪{Su}；I（m，n）是变量m和n的互信息；Y是目标类。被选择的分类器是与目标类I（ψk;Y）具有最大相关性的分类器，同时具有最小冗余度的Su－1，1u－1∑ψi∈Su－1I（ψk;ψi）。

2.1.3 边缘与多样性剪枝

基于边缘和多样性的集成修剪（margin and diversity based ensemble pruning， MDEP）由Guo等人［24］于2018年提出。该方法考虑了两个方面来更好地对分类器集进行重新排序：a）关注绝对边缘较小的示例；b）关注对集成具有较大多样性贡献的分类器。MDEP对分类器进行排序的公式如下：

MDEP（ψk）=∑i［αfm（xi）+（1－α）fd（ψk，xi）］

i|ψk（xi）=yi（3）

其中：α∈［0，1］表示样本的边缘和集合多样性之间的重要性平衡； fm（xi）和fd（ψk，xi）分别是xi的差额和ψk对xi多样性贡献的对数函数，具体公式如下：

fm（xi）=logv（i）yi－v（i）iM（4）

fd（ψk，xi）=logv（1）yiM（5）

其中：yi是从xi中获得最多票数的类别，且yi≠yi。MDEP的局限性是依赖于α的预定义值，该值控制着在关注正确预测硬样本的分类器和关注增加集成多样性的分类器之间的权衡。

2.1.4 AUC-贪婪剪枝

AUC贪婪方法添加提高AUC的基分类器，直到没有任何改进为止［9］。它遵循前向选择过程，从空的优化剪枝集合开始，迭代插入最大化 AUC 的决策树。

2.2 基于多目标优化的规则提取

经过随机森林修剪，剩余规则数量仍相对庞大，如需进一步提升模型可解释性，需要考虑通过进一步缩减规则集的规模。由于模型的准确性和可解释性相互制约，本研究使用多目标优化方法确立多个优化目标来搜索精确性和可解释性相平衡的规则集。在多目标优化中，NSGA-Ⅱ已经是公认具有优异表现的算法，可用于在Patero前沿上寻找精确性和可解释性表现均优的优化规则集［25］。由于传统的NSGA-Ⅱ算法较难在规模较大的解空间寻找最优解，本研究借鉴文献［10］在2021年的研究对NSGA-Ⅱ进行改进，即基于单个指标形成一个候选规则集，并在候选规则集的基础上进行染色体生成，最终得到Patero前沿上的优化规则集。具体方法如下：

2.2.1 规则的染色体表达

本研究将染色体以二进制变量编码形式来代表规则集和规则子集。在染色体的二进制表达形式中，每个元素都为二进制变量，当元素为1时，代表该染色体对应的知识中已被筛选模型选中；当元素为0时，代表该染色体对应的规则中未被筛选模型选中。

2.2.2 优化目标选择

根据以往研究，规则集的性能可从准确性和可解释性两个方向进行评估［10］。准确性代表规则集在预测时的准确程度，建立准确性优化目标QIDE的表达公式如下：

Identification（QIDE）=1－AUCsub（6）

其中：AUCsub表示该染色体对应的规则子集的预测性能，AUCsub计算为受试者工作特征 （ROC） 曲线下的面积。

可解释性表示为专家在认识规则和理解规则上涉及到的指标。规则集的可解释性表现越强，专家就更容易对知识的判别结果产生信任，从而实现机器学习有机融入决策过程。建立可解释性优化目标的表达公式如下：

Interpreability（QINT）=Num_feaoptNum_feacand×Num_ruleoptNum_rulecand（7）

其中：Num_feaopt和Num_feacand分别表示优化规则集中Ruleopt和候选规则集Rulecand中每条规则涉及到的平均特征数；Num_ruleopt和Num_rulecand分别是优化规则集和候选规则集Rulecand中的规则数量；Num_feaoptNum_feacand表示从特征数角度对优化规则子集的评估；Num_ruleoptNum_rulecand表示从规则数量角度评估优化规则子集。

2.2.3 基于单个指标的候选规则提取

由于初始的规则集数量庞大，很难直接提取出具备较高价值的规则集，所以需进行一次初步提取过程，得出候选规则集再进行下一步提取。本研究根据三个指标进行三次从高到低的排序，每次排序会对排名前φ的知识进行标记，其中φ为0到1之间的常数，代表进行标记的比例。三次标记完成后，只有一个标记和没有标记的知识会被去除，两个及以上标记的规则保留作为候选规则集。

2.2.4 初始种群选择

初始种群的选择会影响最终优化迭代帕累托最优解的速率和效果。NSGA-Ⅱ选取初代种群的方法是随机选择，本研究在此基础上基于预筛选的结果进行有指向性的随机选择。根据上一步，候选知识集将包含两次标记、三次标记两类。标记的次数越多，代表知识表现更全面，包含价值更高。因此，可对标记次数多的知识作优先选择，直至形成一条完整的染色体。若初始种群包含N条染色体，则完全随机生成N/2条染色体，另外的染色体将基于不同类别进行有偏好的随机选择。

2.2.5 规则集优化过程

本研究在候选规则集提取和初始种群选择的基础上进行规则子集的多次迭代。使用的NSGA-Ⅱ算法是经典的多目标优化算法，通过模仿生物的进化过程来实现染色体表现的进化，目前被广泛应用于多类优化问题。该算法通过非支配解排序、拥挤度计算和多次迭代进化得到帕累托最优解，并使用交叉、变异和精英选拔在每次进化中寻求更优秀的子代。

3 模型对比实验

信用贷款是一种根据借款人信誉发放的贷款，不需要借款方提供实质性或第三方担保。信用贷款的风险在于低门槛的设置增加借款方的违约行为风险，使得贷款银行蒙受巨大损失［26］。建立有效的信用贷款风险评估模型可以辅助决策者作出正确判断，进而降低违约行为对正常信用贷款的影响。信用贷款风险评估以二分类问题为主，传统的统计计量方法已不能满足贷款银行对高精确率的要求，而复杂的黑盒模型因缺乏可解释性而无法受到决策者的信任［27］。因此，在信用贷款风险评估领域推广基于机器学习的透明模型是关键研究方向。为验证本研究中PRFRE模型在解释随机森林的有效性，本研究选取金融领域信用欺诈风险场景作为实证研究的场景，选用三个信用贷款风险评估领域被广泛研究的公开数据集进行实验对比研究。数据集均为二分类数据集，用于区分样例是否存在信用风险，不存在风险的视为白样本，存在风险的视为黑样本。

3.1 数据集描述

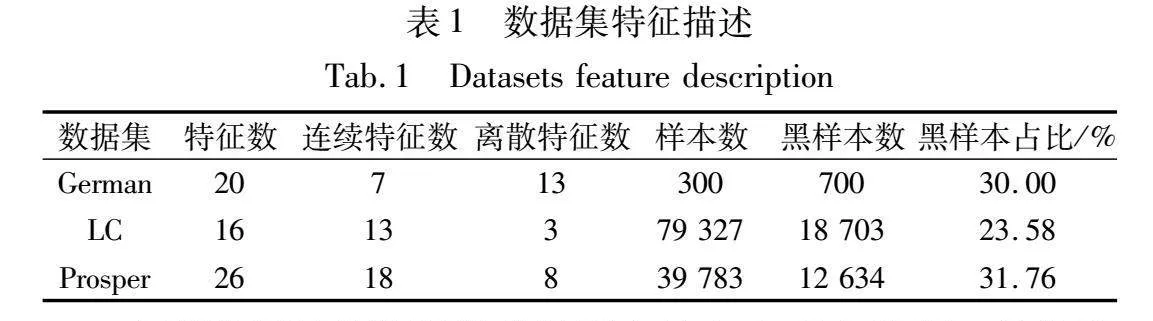
本研究共采用German、Lending Club（LC）以及Prosper三个数据集，均为信用风险评估领域的二分类数据集，具体特征如表1所示。German德国信贷数据集来源于机器学习领域权威的UCI数据库。LC数据集为美国最大的P2P在线贷款平台Lending Club中2017年的全部借款记录。Prosper数据集来源于美国知名在线贷款平台Prosper的2013年至2014年的借款记录。使用的三个数据集在信用风险评估领域研究中被广泛应用，具有一定的代表性［28］。

本研究使用的数据集预处理方法包含多个步骤。首先数据标签分为正常标签和风险标签，分别用0和1表示。其余相似的标签将并入这两类标签之一，不相似标签的样本将被消除。其次，将缺失率超过40%以上的特征和包含缺失值的样本进行删除。最后，为保证数据类别的均衡，本研究采取欠采样的方法进行处理。此外，本研究还对数据集进行归一化、编码等针对性处理，由于篇幅限制没有作详细说明。

本研究将数据分为训练集、测试集和验证集三个部分。其中训练集和测试集采用五折交叉验证测试方法来验证模型，以保证随机数据分区不影响实际评估结果；验证集从数据集中随机抽取且不参与交叉验证，用于后续实验测试规则性能。

3.2 模型评价指标与参数选取

信用风险分类可以有效地构建为二元分类问题来预测违约概率。因此，评估结果可以分为四个不同的类别：真阳性（TP）、假阳性（FP）、真阴性（TN）和假阴性（FN）。TP 指的是实际存在风险被准确分类的情况；FP 描述的是正常交易被错误地标记为存在风险的情况；TN 表示正常交易被正确识别的情况；FN 反映实际默认值被错误标记为正常交易的情况。

本研究采用机器学习领域常见的评估指标来评估模型预测和解释信用风险的有效性。根据方法部分的描述，评估解释模型的性能时需要考虑形成规则集的准确性和可解释性两个方面。在准确性评估方面，选择召回率（recall）和平衡F1分数（F1-score）指标来评估模型预测风险的能力，并采用精确率（Acc）和受试者工作特征 （ROC） 曲线下面积 （AUC） 等指标来衡量模型的整体性能。ROC曲线是通过对用于计算假阳性率（FPR）和真阳性率（TPR）的决策函数设置不同的阈值来获得的，并且使用梯形规则计算AUC。在可解释性评估方面，本研究将规则集的平均特征数、平均规则数量作为评估指标。精确率、召回率和F1分数指标定义如下：

precision=TPTP+FP（8）

recall=TNTP+FN（9）

F1=2×precision×recallprecision+recall（10）

经过参数调优测试，本研究提出模型的参数如表2所示。

3.3 实验结果分析

3.3.1 随机森林剪枝分析

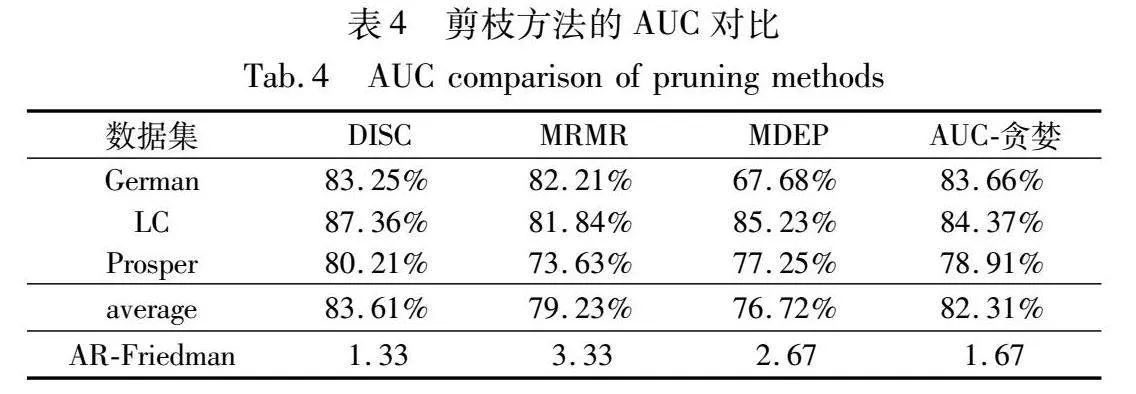
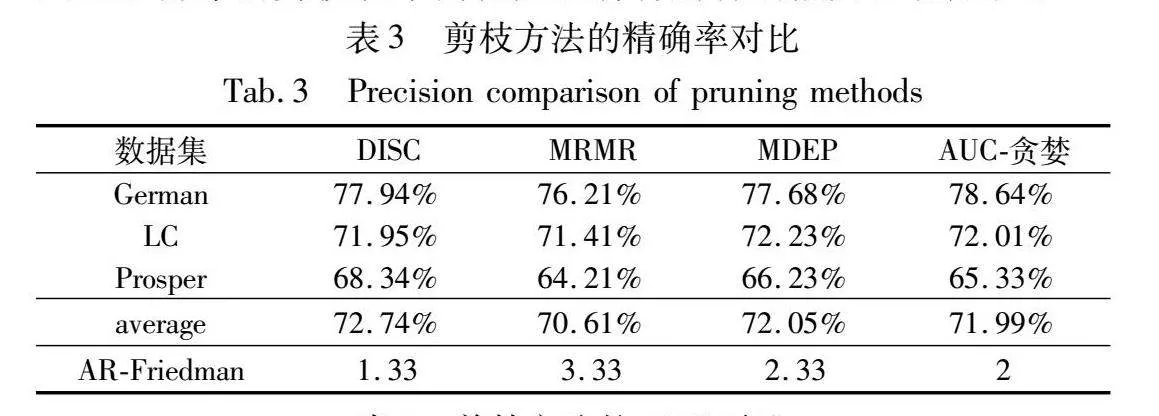
表3展示了本研究使用四种剪枝技术的精确率对比。如表所示，每个数据集均只有一种方法达到了最佳精度。在三个数据集中，German数据集使用AUC-贪婪方法达到了最优性能，LC数据集使用MDEP剪枝方法达到最优性能，Prosper数据集使用DISC方法达到了最优。为了区分出剪枝技术的性能，本研究进行Friedman检验的平均序值（AR-Friedman）并将结果展示在表3中的最后一行。测试结果表明，DISC 方法实现了最佳性能，MDEP方法其次，AUC-贪婪方法排列第三，而 MRMR 方法表现出最低的性能。表4展示了不同修剪方法的AUC 对比结果。同样，每个数据集均只有一种方法达到了最佳精度。Friedman检验排名最好的是DISC和AUC-贪婪方法，MDEP和MRMR方法排名靠后。综上所述，AUC-贪婪方法在小数据集上的表现突出，而DISC剪枝方法的综合表现较强，反映出基于排序的剪枝技术简化随机森林解释的能力和稳定性。

3.3.2 规则提取分析

为对比模型整体的性能，实验选取五种基于随机森林的规则提取方法作为参照，与本研究提出的模型进行对比，参照模型介绍如下：

a）RF+HC：利用随机森林（RF）形成树模型，结合爬山算法（HC）对高可解释性规则进行筛选，提取可解释性强的规则子集［19］。

b）RF+DHC：RF+HC方法的变体，不仅考虑到叶节点的规则，同时考虑到中间节点的规则，并且在选择最优子集时确定初始规则［29］。

c）Rulefit：结合树集成模型与线性模型形成规则，从决策树中创建规则，并使用原始特征与规则进行线性拟合，可处理分类任务［30］。

d）IRFRE：从随机森林中提取规则，并根据规则的精确度（Acc）、规则覆盖度、规则特征数和规则数量利用改进的NSGA-Ⅱ方法寻找最优解，得到帕累托最优前沿［31］。

e）TSREM：将规则提取分为局部规则提取和全局规则提取两个环节，其中局部规则提取对每个规则的性能进行对比并精简，全局规则提取考虑规则集的整体性能，以实现规则集的优化［10］。

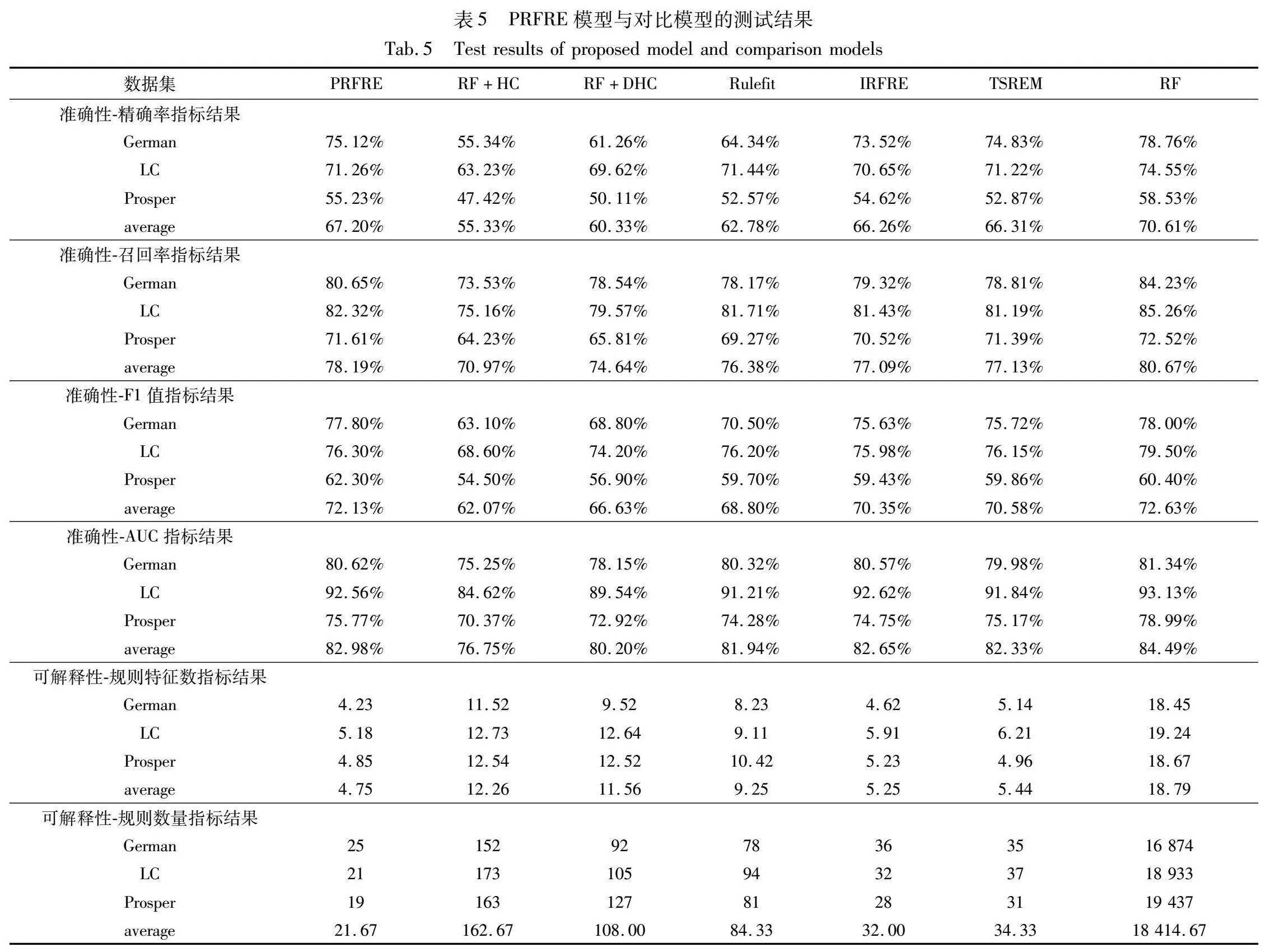
对于各类实验的参数设置，所有集成树模型的最大深度设置为10，生成决策树数量为100，确保实验的基础树模型保持一致。在RF+HC， RF+DHC， Rulefit， IRFRE， TSREM的设置上，令算法重复5次，每次2 000步，其余参数依照论文给出的最优设置进行配置。实验得出的结果如表5所示。

首先，从准确性上对实验结果展开分析。实验选取精确率、召回率、F1值和AUC作为模型在准确性上的性能评估指标，指标的含义和公式已在32节给出。根据表中的结果可得到以下结论：

a）精确率、召回率、F1值和AUC表现最优的多为随机森林模型，随机森林模型为规则提取的源模型，证明模型的可解释性会牺牲一定的模型准确性。

b）PRFRE模型在其他对比规则模型中的精确率、召回率、F1值和AUC均为最优的模型，且指标表现接近源模型，说明PRFRE模型能够最大程度还原源模型的准确性和预测能力。

其次，在可解释性上对实验结果进行分析。实验选取模型规则特征数、规则数量作为评估模型可解释性指标，具体含义已在文章的第2章给出。根据表5的结果可得到以下结论：

a）随机森林模型的可解释性指标表现远低于其他模型，平均规则特征数和平均规则数量已分别达到18.79和18 41467，明显不具备可解释性。

b）PRFRE模型在规则特征数和规则数量上表现均为最优，平均规则特征数和平均规则数量分别为4.75和21.67，具有极强的可解释性。

综上所述，随机森林模型虽然在准确性上具有一定优势，但可解释性上的缺陷导致其无法受到决策者信任，模型的应用领域受限；而PRFRE模型在尽可能保证源模型准确性的基础上极大地提升了模型可解释性，辅助决策者理解模型和制定措施。另外，实验模型的准确性和可解释性具有相互制约的效果，即模型的可解释性提升会牺牲部分模型的准确性。

3.3.3 参数设置分析

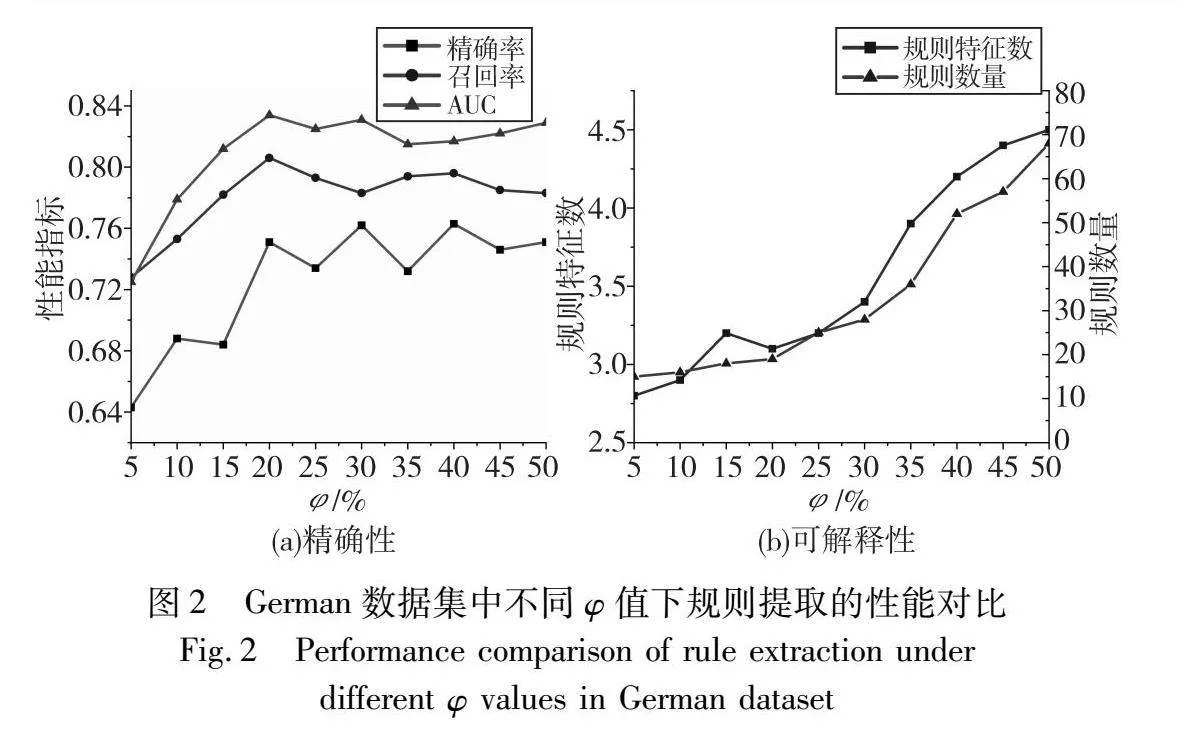
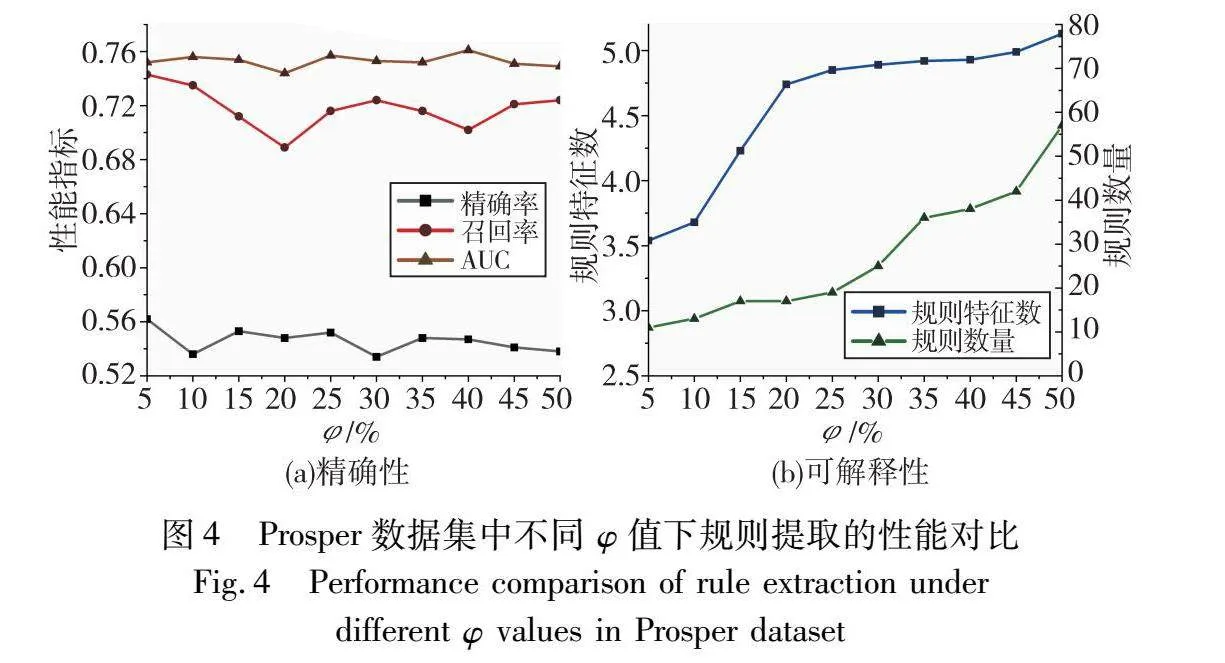
规则预筛选是通过对规则的每个指标的性能进行排名比较，去除不符合条件的规则后得到规则数量相对减少的候选规则，从而提高多目标优化对结果的收敛性和多样性。该实验用

于证明φ的不同取值对于PRFRE模型输出规则的性能影响，其中φ值为每个指标的选取阈值，φ的作用已在本文第2章进行介绍。三个数据集在不同φ值下的优化规则集的性能如图2～4所示。根据图中的对比分析可得出，φ值对规则集性能存在正面影响，图2可以清晰地显示φ值变化对于规则集精确性的影响；另外，图3和4的精确性部分体现出φ值对可解释性上的影响更为显著。这是因为φ值与规则数量和特征数正相关，φ值的变化影响优化问题的解空间，并间接影响通过规则提取时优化规则集的性能。在实际应用中，专家可根据对规则性能的偏好来确定φ的取值，若需要可识别能力与可理解能力较为均衡的规则，适合将φ值调整至20%～25%；若需要可识别能力或可理解能力在单方面指标表现优异的规则，则可将φ值设置为5%～10%。

3.3.4 模型输出与决策过程

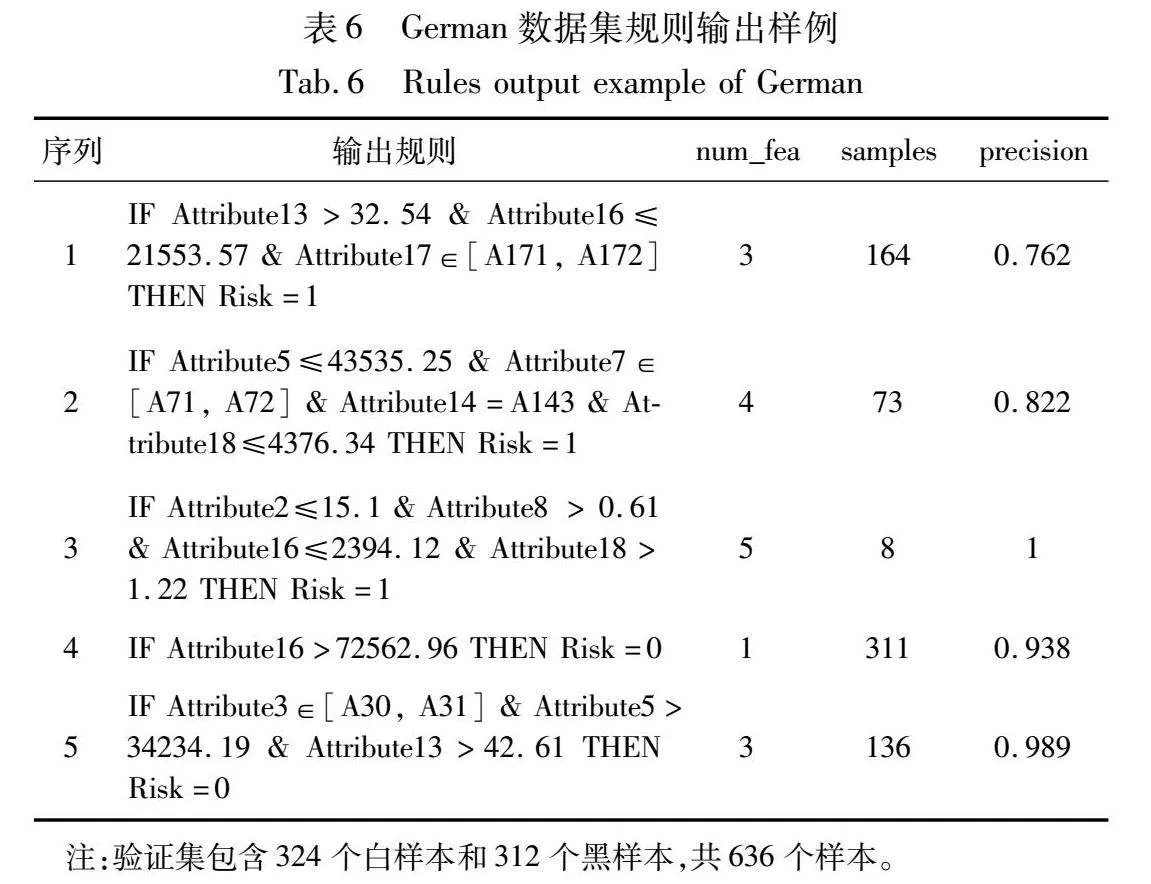
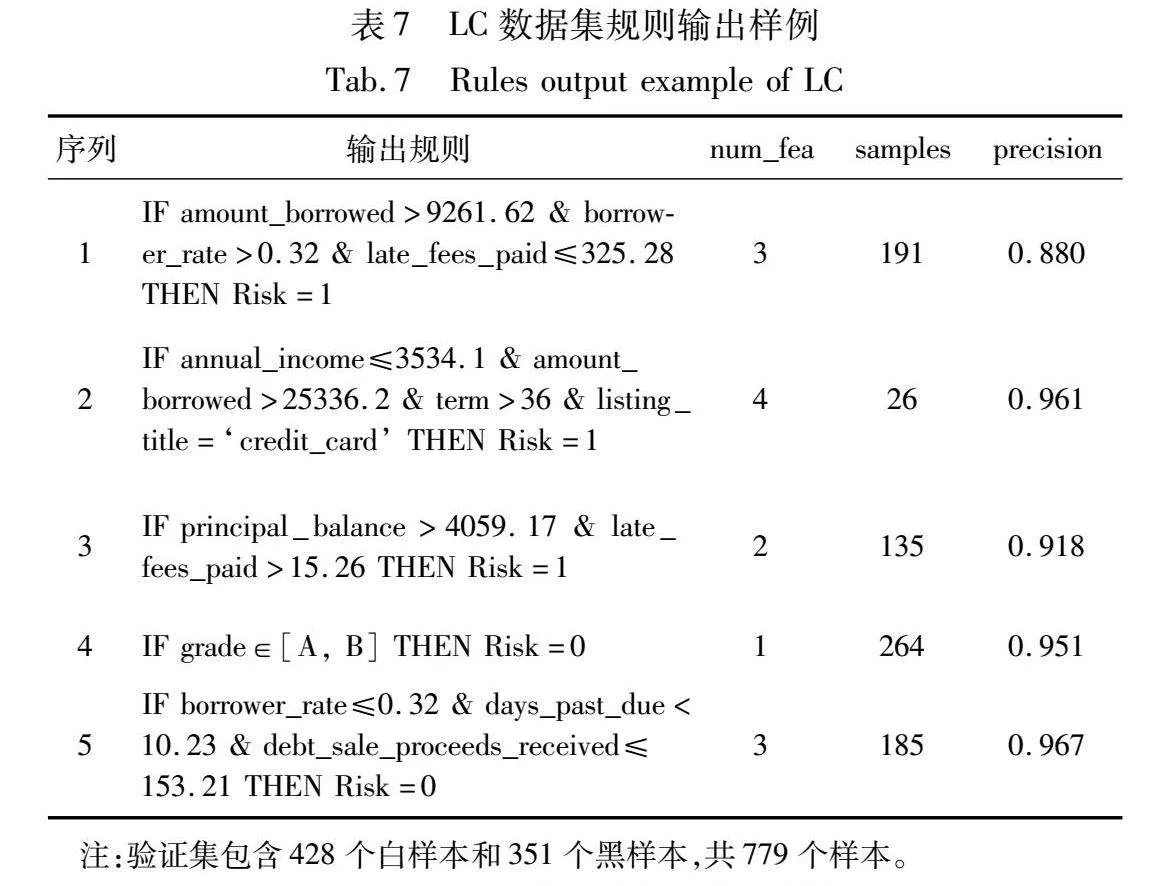
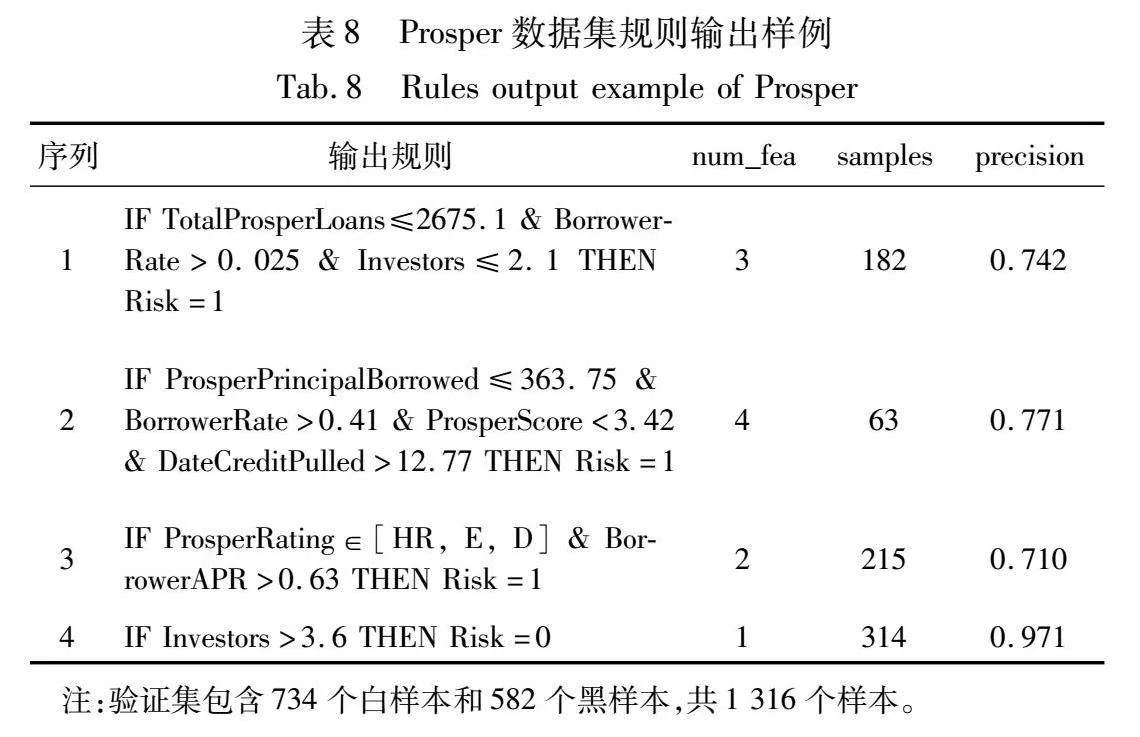
在实际场景中，模型输出规则既可以帮助决策者理解模型的推理逻辑，也可以代替不透明模型辅助决策者进行决策。为展现规则提取模型输出的结果及规则参与决策的过程，本节将展示从规则模型中提取的规则样例，以及介绍决策者根据规则进行决策的过程。生成规则的性能和有效性可以通过前面讨论的准确性和可解释性来验证。本研究在German、LC和Prosper数据集上随机提取一折实验结果并展示部分输出规则，结果如表6～8所示，其中num_fea代表规则特征数，samples为规则命中样本数，precision为规则精确率。为展示规则的性能，保留部分样本作为验证集对规则的性能进行评估，给出规则的特征数、命中的样本数和精确率信息。如表所示，规则的特征数较少，可供决策者快速提取可研究的特征交叉信息；精确率均保持在70%以上，保证了规则的高价值特性。

由表6～8所示，本研究模型输出规则将特征数控制在4个以内，以保证规则能够被人类所理解。有存在个别规则特征数较多的规则，例如表6中的第3条规则有5个特征且只命中了8个样本，但由于其具有极高的精确率，考虑到存在的特殊类型的贷款情况，故该规则被保留用于向决策者展示存在于贷款领域的小概率事件。有部分规则涉及的规则较少，命中的样本数较多，体现了单个特征的高重要性或交叉特征的强交互关系。

通过观察规则的特征出现频率和逻辑条件可以总结出贷款风险的部分规律。有多条规则均涉及到与借款利率相关的特征，且进一步观察发现高借款利率往往伴随着贷款风险的增加。这是因为借款利率越高，还款的金额就越大，越容易出现违约风险，符合贷款风险评估的逻辑。

当新的贷款交易对象出现时，可以将用户的数据特征与规则库内的规则特征进行条件匹配来判断哪些规则可以参与决策，并通过投票形式对用户风险分类进行结果输出，后续将实际调查结果反馈给规则库来对规则的表现进行更新。决策者可以根据规则表现，灵活调整规则库中激活的规则，特别是其在历史使用中的表现。

4 结束语

随机森林模型具有良好的灵活性、应用性以及卓越的预测性能表现，也可从树结构中提取IF-THEN形式的决策规则，然而原模型提取规则的数量众多且可解释性差，需要对规则作进一步处理以提高可解释性，从而加强实际场景中的应用效果。本研究提出了基于剪枝随机森林的规则提取模型（PRFRE），首先对训练好的随机森林模型进行集成剪枝，减少基决策树数量以提高提取规则的效果，再使用基于多目标优化的规则提取方法，从候选规则集中搜索具有高准确性和高可解释性的优化规则集。本研究使用信用风险评估领域具有代表性的三个数据集进行实验。首先对比了四个剪枝技术的效果，结果证明DISC剪枝方法和AUC-贪婪方法在对随机森林剪枝任务上表现优秀。为证明PRFRE模型的有效性，本研究选取四个规则提取模型进行对照实验，结果表明PRFRE模型输出规则在不降低准确性的基础上，大幅提升了可解释性。模型对比实验证明了PRFRE模型在提取准确性和可解释性均衡的优化规则集上的先进性。

随着可解释技术（XAI）发展，面向黑盒模型的规则提取研究使随机森林模型的可解释性优化成为可能，而现有针对随机森林模型的规则提取研究无法兼顾精确性与可解释性。本研究通过融合集成剪枝与多目标优化算法，解决了随机森林模型可解释性不强的问题。该方法适用于解决如金融欺诈检测、医疗诊断等领域中对模型的准确性和可解释性同时存在要求的二分类问题，对促进人机交互的发展具有重要意义。

本研究提出的PRFRE模型在训练效率和树集成模型选择上具有一定局限性，包括目前模型只适用于二分类数据集，应用领域局限于欺诈检测领域，且只可对基于随机生成的集成树模型进行规则提取。未来可以在以下两个方面进行下一步研究：一是将基于多目标优化算法的规则提取推广至其他基于顺序依赖的树集成模型中，如XGBoost算法；二是探究增量规则提取的方式，以提高规则提取在连续场景中的使用效果。

参考文献：

［1］刘艳红. 人工智能的可解释性与AI的法律责任问题研究 ［J］. 法制与社会发展， 2022， 28（1）： 78-91. （Liu Yanhong. On the explainability and legal liability of artificial intelligence ［J］. Law and Social Development， 2022， 28（1）： 78-91.）

［2］Saeed W， Omlin C. Explainable AI （XAI）： a systematic meta-survey of current challenges and future opportunities ［J］. Knowledge-Based Systems， 2023， 263： 110273.

［3］孔祥维， 唐鑫泽， 王子明. 人工智能决策可解释性的研究综述 ［J］. 系统工程理论与实践， 2021， 41（2）： 524-536. （Kong Xiangwei， Tang Xinze， Wang Ziming. A survey of explainable artificial intelligence decision ［J］. Systems Engineering-Theory & Practice， 2021， 41（2）： 524-536.）

［4］Czajkowski M， Jurczuk K， Kretowski M. Steering the interpretability of decision trees using lasso regression-an evolutionary perspective ［J］. Information Sciences， 2023， 638： 118944.

［5］Ribeiro M T， Singh S， Guestrin C. “Why should I trust you？”： explaining the predictions of any classifier ［C］// Proc of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM Press， 2016： 1135-1144.

［6］唐蕾， 牛园园， 王瑞杰， 等. 强化学习的可解释方法分类研究 ［J］. 计算机应用研究， 2024， 41（6）：1601-1609. （Tang Lei， Niu Yuanyuan， Wang Ruijie，et al. Classification study of interpretable methods for reinforcement learning ［J］. Application Research of Computers， 2024， 41（6）：1601-1609.）

［7］Khalifa F A， Abdelkader H M， Elsaid A H. An analysis of ensemble pruning methods under the explanation of random forest ［J］. Information Systems， 2024， 120： 102310.

［8］Aria M， Cuccurullo C， Gnasso A. A comparison among interpretative proposals for random forests ［J］. Machine Learning with Applications， 2021， 6： 100094.

［9］Sagi O， Rokach L. Approximating XGBoost with an interpretable decision tree ［J］. Information Sciences， 2021， 572： 522-542.

［10］Dong Lu’an， Ye Xin， Yang Guangfei. Two-stage rule extraction method based on tree ensemble model for interpretable loan evaluation ［J］. Information Sciences， 2021， 573： 46-64.

［11］Boruah A N， Biswas S K， Bandyopadhyay S. Rule extraction from decision tree： transparent expert system of rules ［J］. Concurrency and Computation： Practice and Experience， 2022， 34（15）： e6935.

［12］Ghafari S M， Tjortjis C. A survey on association rules mining using heuristics ［J］. WIREs Data Mining and Knowledge Discovery， 2019， 9（4）：e1307.

［13］Li Bo， Qi Peng， Liu Bo，et al. Trustworthy AI： from principles to practices ［J］. ACM Computing Surveys， 2023， 55（9）： 1-46.

［14］左明月. 基于集成学习和SHAP优化的个人信贷违约可解释预测模型 ［D］. 济南：山东大学， 2023. （Zuo Mingyue. Interpretable prediction model of personal credit default based on ensemble learning and SHAP optimization ［D］. Jinan：Shandong University， 2023.）

［15］马亚雪， 王嘉杰， 巴志超， 等. 颠覆性技术的后向科学引文知识特征识别研究——以基因工程领域为例 ［J］. 图书情报工作， 2024， 68（1）： 116-126. （Ma Yaxue， Wang Jiajie， Ba Zhichao，et al. Research on the knowledge feature identification of disruptive technologies from its backward scientific citations： taking the field of genetic engineering as an example ［J］. Library and Information Service， 2024， 68（1）： 116-126.）

［16］Chipman H A， George E I， McCulloch R E. Making sense of a forest of trees ［J］. Computing Science and Statistics， 1998： 84-92.

［17］Mohammed A M， Onieva E， Woz＇niak M. Selective ensemble of classifiers trained on selective samples ［J］. Neurocomputing， 2022， 482： 197-211.

［18］Mohammed A M， Onieva E， Woz＇niak M，et al. An analysis of heuristic metrics for classifier ensemble pruning based on ordered aggregation ［J］. Pattern Recognition， 2022， 124： 108493.

［19］Mashayekhi M， Gras R. Rule extraction from random forest： the RF+HC methods ［C］// Proc of the 28th Canadian Conference on Artificial Intelligence. Cham： Springer， 2015： 223-237.

［20］李海林， 廖杨月， 李军伟， 等. 高校杰出学者知识创新绩效的影响因素研究 ［J］. 科研管理， 2022， 43（3）： 63-71. （Li Hailin， Liao Yangyue， Li Junwei，et al. A study of the influence factors of knowledge innovation performance of distinguished scholars in colleges and universities ［J］. Science Research Management， 2022， 43（3）： 63-71.）

［21］Wang Yuyan， Wang Dujuan， Geng Na，et al. Stacking-based ensemble learning of decision trees for interpretable prostate cancer detection ［J］. Applied Soft Computing， 2019， 77： 188-204.

［22］Cao Jingjing， Li Wenfeng， Ma Congcong，et al. Optimizing multi-sensor deployment via ensemble pruning for wearable activity recognition ［J］. Information Fusion， 2018， 41： 68-79.

［23］Martínez-Muoz G， Hernández-Lobato D， Suárez A. An analysis of ensemble pruning techniques based on ordered aggregation ［J］. IEEE Trans on Pattern Analysis and Machine Intelligence， 2009， 31（2）： 245-259.

［24］Guo Huaping， Liu Hongbing， Li Ran，et al. Margin & diversity based ordering ensemble pruning ［J］. Neurocomputing， 2018， 275： 237-246.

［25］Deb K， Pratap A， Agarwal S，et al. A fast and elitist multiobjective genetic algorithm： NSGA-Ⅱ ［J］. IEEE Trans on Evolutionary Computation， 2002， 6（2）： 182-197.

［26］迟国泰， 王珊珊. 基于XGBoost的中国上市公司违约风险预测模型 ［J］. 系统管理学报， 2024，33（3）：735-754. （Chi Guotai， Wang Shanshan. Default risk prediction model for Chinese listed companies based on XGBoost ［J］. Journal of Systems & Management， 2024，33（3）：735-754.）

［27］贾颖， 赵峰， 李博， 等. 贝叶斯优化的XGBoost信用风险评估模型 ［J］. 计算机工程与应用， 2023， 59（20）： 283-294. （Jia Ying， Zhao Feng， Li Bo，et al. XGBoost optimized by Bayesian optimization for credit scoring ［J］. Computer Engineering and Applications， 2023， 59（20）： 283-294.）

［28］Hilal W， Gadsden S A， Yawney J. Financial fraud： a review of anomaly detection techniques and recent advances ［J］. Expert Systems with Applications， 2022， 193： 116429.

［29］Mashayekhi M， Gras R. Rule extraction from decision trees ensembles： new algorithms based on heuristic search and sparse group Lasso methods ［J］. International Journal of Information Technology & Decision Making， 2017， 16（06）： 1707-1727.

［30］Friedman J H， Popescu B E. Predictive learning via rule ensembles ［J］. The Annals of Applied Statistics， 2008， 2（3）： 916-954.

［31］Wang Sutong， Wang Yuyan， Wang Dujuan，et al. An improved random forest-based rule extraction method for breast cancer diagnosis ［J］. Applied Soft Computing， 2020， 86： 105941.