以数学为主导的多学科融合教学促进计算思维培养：实施框架与课例开发

【摘 要】 STEAM理念与计算思维融合教学（STEAM+CT）已成为K12阶段培养计算思维的重要方式.在5E教学模式指导下，提出数学为主导的STEAM+CT教学实施框架，旨在提高学习者的计算思维能力.在该教学实施框架下，开发了“探索分形几何奥秘”课例.课例能够将不同学科知识建立有机衔接，教学过程能有效指向计算思维核心能力的培养，这为未来STEAM+CT教学提供新路径.

【关键词】 数学；计算思维；STEAM；分形几何

1 引言

过去二十年，随着信息化社会的发展与数字技术的快速变革，人们的生产生活乃至思维方式都发生了巨大改变.在此背景下，社会对人才培养提出新的要求，计算思维（Computational Thinking，简称CT）引起各国的高度关注.美国数字承诺教育技术中心认为计算思维是21世纪学生参与科技社会的必备技能，并要求教育者为学生提供参与计算实践的机会［1］.2022年欧盟委员会发布《义务教育计算思维研究》报告，指出奥地利、法国等在内的25个欧洲国家已经将计算思维纳入现行法定义务教育课程［2］.在欧洲以外，澳大利亚、新加坡等国也制定了相关政策，将计算思维引入K12教育以提升学生计算思维能力.如今，计算思维在我国也引起了重视.高中信息技术课程标准（2017年版）以及义务教育信息科技课程标准（2022年版）都已将计算思维列入学科核心素养.

STEAM教育是以多学科整合的方式培养学生科学、技术、工程、艺术与数学素养的一种技术教育，其有利于学生运用跨学科的思维解决现实问题.而计算思维与包括数学、科学和人文社科在内的所有学科都相关［3］，这与STEAM理念相契合.随着计算思维逐渐被认为是STEAM问题解决的关键技能，教育者开始通过多学科融合教学的形式将计算思维融入学校课程.但已有教学往往是以技术或工程学科作为课题开展，较少有以数学为主导的教学.我国《普通高中数学课程标准（2017版）》在论及课程内容时强调要加强数学学科与其他学科的联系，让学生认识数学模型在科学、工程技术诸多领域的作用.《义务教育数学课程标准（2022年版）》首次提倡在综合与实践领域落实跨学科活动，并在论及核心素养内涵时首次提到计算思维一词.可见，我国数学课程改革正朝着与其他学科融合以促进学生具备21世纪公民基本技能的方向发展.因此，如何以数学学科为主导实行多学科融合教学，以此提升学生计算思维能力，将成为未来国内计算思维研究的发展方向，具有重要的理论与实践价值.2 理论视角：国内外研究综述

2.1 计算思维与STEAM教育

2006年卡内基梅隆大学周以真教授提出计算思维是一种运用计算机科学基本概念来解决问题、设计系统和理解人类行为的方式，是面向所有人的一项普适技能［3］.此后学者就计算思维展开广泛的研究与讨论.美国国际教育技术协会和计算机科学教师协会指出计算思维是一个问题解决的过程［4］.英国计算课程工作小组认为计算思维是一种涉及逻辑推理的认知思维过程并指出计算思维与所有学科中涉及的思维技能都相关［2］.尽管学者尚未就计算思维的定义达成一致，但不难看出计算思维是一种思维方式，其内在价值是问题解决.计算思维是一种兼具科学、数学等多学科思维的分析思维，是能够将STEAM教育中不同学科思维互补融合的综合性思维［5］.由于学生课业负担较重，在K12阶段专门开设计算思维培养课程是难实现的，因此教育研究者从计算思维与STEAM教育内在的一致性出发，将计算思维融入STEAM教育，形成面向计算思维培养的多学科融合教学（STEAM+CT）.融入计算思维的STEAM教育不仅能够促进学生对不同学科内容的学习，同时也是提升学生计算思维能力的有效方式.可见，STEAM教育在计算思维培养中应用的优势为计算思维在基础课程中的落实提供了路径.

2.2 数学与STEAM+CT教育

如今STEAM教育呈现出不公平的学科代表性，尤其是数学学科往往仅作为操作性学科来辅助计算，并未实现真正意义上的融入［6］.数学已经被公认为是科学、技术等学科的基础，能用数学思维分析现实问题理应成为STEAM教育所追求的目标.纵观如今在STEAM+CT教育理论下开发的课例，数学更是处于与技术、工程等学科不平等的位置.如今越来越多学者开始关注数学与计算思维之间的关联，并意识到数学思维与计算思维在问题解决、建模、数据分析以及统计概率四个方面具有共同的思维模式［7］.同时实证研究表明，将计算思维引入数学课堂能够有效提高学生的问题解决能力，并为数学内容的学习提供有利的支持［8］，促进数学核心素养的提升.从问题解决角度来看，尽管数学思维与计算思维有所差异，但它们更多体现了某种一致性.PISA项目组在《PISA2022数学框架》中融入了计算思维教育评估的内容，用于评估数学学科中学生的计算思维能力.国内也有不少学者强调将计算思维纳入数学教育的重要性［9-10］.可见在数智时代，将计算思维融入数学素养将会是未来发展的必然趋势，因此有必要重视数学这一基础学科在STEAM+CT教育中的作用.

3 实施框架：以数学为主导的STEAM+CT教学

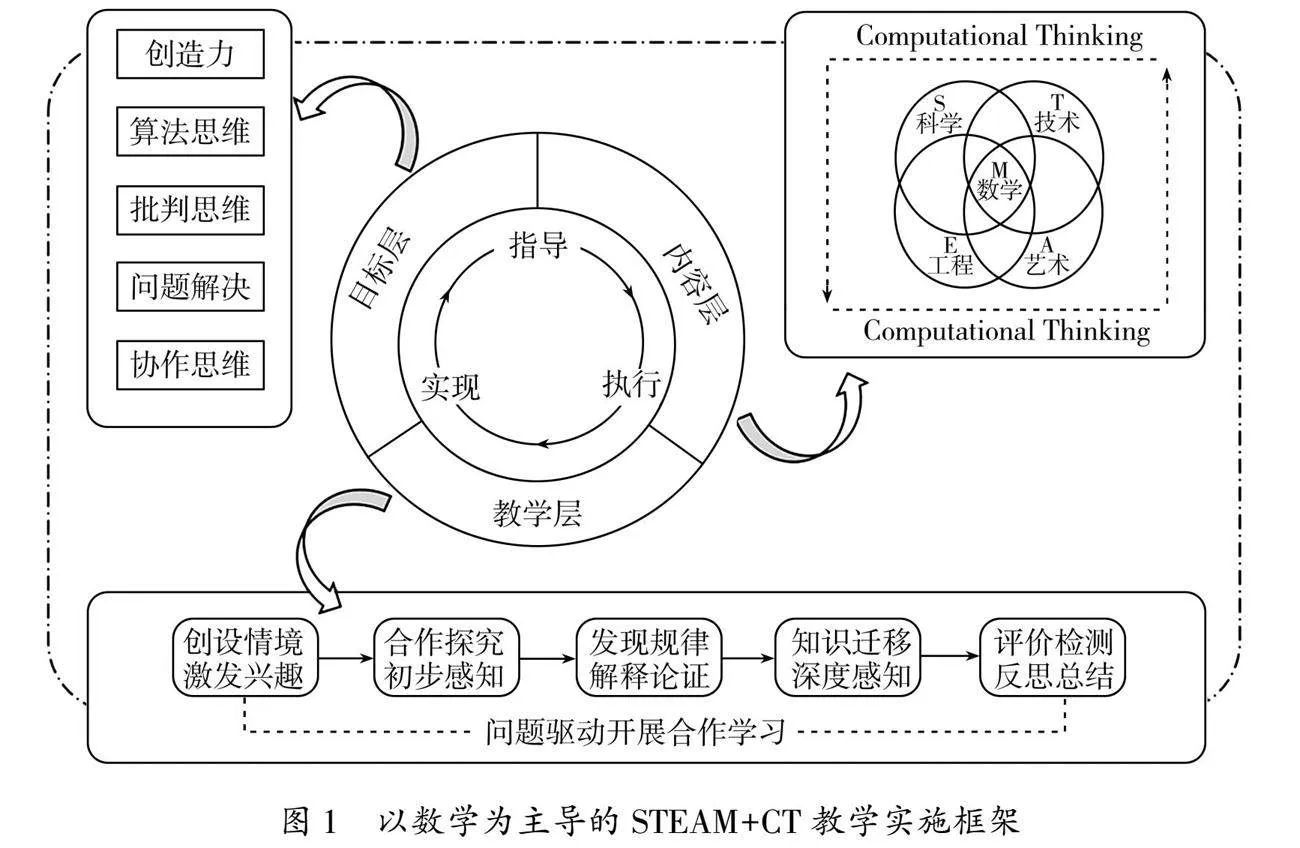
以数学为主导的STEAM+CT教学，是指由教师或团队在数学课程中选择适合内容作为教学的中心，运用数学、科学、技术等多学科知识，以提升学生计算思维为目标而开展的教学.5E教学模式是基于建构主义的探究式教学模式，它包括参与、探究、解释、迁移与评价五个教学环节，如今已成为STEAM教育的主流模式.本研究在梳理国内外相关文献的基础上，参照5E教学模式总结出以数学为主导的STEAM+CT教学的实施框架（图1）.

3.1 目标层：指向计算思维核心能力培养

本研究以Korkmaz［11］等提出的计算思维五大核心技能作为教学培养目标.其中，创造力是指产生新思想、发现和创造新事物的能力.算法思维包含理解、建立、优化与应用算法的一系列逻辑步骤.批判思维是决定行为的反思性思维，通过批判性思考对多种方案进行合理地判断与决策.问题解决能力是制定解决方案、实现计划方案的能力，并在解决某一特定情境的问题后，能将解决方案迁移到另一个相似情境中去.协作思维是通过交流合作最大化个人和他人学习成果的能力.

3.2 内容层：基于数学学科的内容选取

目标层指导下内容的选取需以数学为核心，从数学与其他学科的关联处入手，实现各门学科知识的有机融合.数学教材无论是在正文处还是在例题、专栏处都呈现了大量跨学科素材，这些素材来源于自然科学、工程技术等学科，这为以数学为主导的STEAM+CT教学开展提供了有力支持.在内容选取上，教师还可以主动和不同学科教师之间进行学科交流，通过跨学科教研活动寻找教学立足点.

3.3 教学层：立足5E教学模式开展合作学习

合作学习是STEAM+CT教学中常用的教学活动，且被证实能够有效提高学生计算思维能力.故本教学实施框架将合作学习作为主要活动方式.在5E教学模式指导下，教学流程分五步：第一，创设情境，激发兴趣.通过创设真实情境，激发学生的探究兴趣.第二，合作探究，初步感知.在教师的指导下，让学生分组尝试自主探究，初步感知学习内容.第三，发现规律，解释论证.学生将小组自主探究后发现的规律予以说明，师生合作交流共同探讨规律背后的知识原理.第四，知识迁移，深度感知.学生通过合作深度感知学习内容，尝试将所学知识迁移到其他领域.第五，评价检测，反思总结.通过学习反思等教学策略，深化知识理解.通过多样化的评价方式，检测课堂教学目标的实现情况.

4 课例开发：探索分形几何奥秘

人教A版、沪教版等高中数学新教材在数列章节均呈现了科赫雪花曲线、 谢尔宾斯基三角形等多个分形图形.本案例以数学分形图形的探究为主线，带领学生观察自然界中的分形，感知分形在各门学科中的应用.本课例预设分配2个课时，数学教师在熟悉所需的其他学科知识基础上，可独自展开本课教学.本课也可由多位老师共同协作展开教学.

4.1 能力目标与学科内容分析

能力目标以计算思维为核心，发展计算思维的同时提升数学核心素养.包括培养创造力，通过动手创造分形艺术品提升设计与创新能力；培养算法思维，通过自定义函数以及一系列循环、分支结构的编程语句，实现分形图形的绘制，以此提升直观想象核心素养；培养批判思维，在数学推理和分析过程中判断方法的正误，通过比较实现方法优化等，以此提升逻辑推理、数学运算等核心素养；培养问题解决能力，用数学知识探讨分析图形性质，以此提升数学抽象等核心素养；培养协作思维，通过小组成员的协调分工、合作交流共同完成课堂学习任务.

学习内容包括STEAM多学科内容.数学主要了解分形几何，通过数列与极限的知识探究科赫雪花、谢尔宾斯基三角形等分形图形；科学主要感知大自然与人体中的分形结构，例如细胞繁殖分裂过程中的分形等；技术学习Python编程知识，包括递归算法、Turtle绘图库等；工程了解程序开发的一般流程，包括开发环境选择、功能模块设计等；艺术鉴赏分形美术作品，感知分形魅力.

4.2 学习者分析

本课可设置在数列章节学习之后，授课对象为高二学生.在核心素养发展上，学生经过高中内容的学习，各门学科的核心素养与思维能力都得到发展.在先验知识掌握上，学生已学习本堂课所需的必需知识，如数学的数列知识、信息技术的算法与Python程序语言等.

4.3 教学活动设计

在以数学为主导的STEAM+CT教学实施框架指导下开展本课的教学.各教学环节涉及的学科内容及对应培养的计算思维核心能力如图2所示.

4.3.1 创设情境，激发兴趣

师生活动：教师呈现大自然中的分形图，引导学生观察图片中物体的共同特点，随后简要介绍分形结构：分形结构依照某种固定的规则，不断延伸或不断细化下去得到的图像，将与最初的图像高度相似.

问题1：大自然中存在着大量的分形结构.而我们的人体其实也是分形的杰作，你们能发现人体中的分形结构吗？

师生活动：教师让学生相互讨论，思考人体中的分形结构.以细胞分裂为例，通过视频呈现细胞有丝分裂五个时期的过程图示.不难看出经过一个细胞周期形成的两个子细胞中遗传物质与母细胞完全相同.母细胞包含与其自身相似的子细胞的全部信息，这就是分形结构.教师指出分形结构的背后蕴含着大量数学知识，并带领学生共同探讨.

设计意图 通过自然界事物中分形的展示，给学生带来视觉冲击，让学生直观感受到分形的艺术之美.通过细胞分裂揭示人体内的分形奥秘，进一步激发学生的学习动机.

4.3.2 合作探究，初步感知

问题2：科赫雪花是一种典型的分形图形，它由瑞典数学家科赫首次提出.我们就从科赫雪花出发走进分形几何的大门.请观察科赫雪花的图案，思考我们如何操作可以得到雪花图形？

师生活动：教师引导学生明确科赫雪花的形成过程：第一步，绘制一个等边三角形；第二步，对等边三角形每条边三等分处理，并以中间的一条线段为底边向外作等边三角形；第三步，对新得到的三角形重复第二步操作，无限多次重复操作便可得到雪花曲线.

任务1：小组合作编写雪花曲线绘制程序.

师生活动：科赫雪花形成过程中需对已经三等分的线段再次进行三等分操作，这与计算机中的递归算法相似.教师向学生讲解递归算法：递归算法是一种通过重复将问题分解为同类的子问题从而解决问题的方法，其特征在于直接或间接调用“自身”.随后教师向学生详细介绍Python绘图模块Turtle以及常见绘图函数.在教师指导下，各小组进行代码块设计、工程文件创建，并完成代码编写.

问题3：从多次迭代后的雪花曲线中，大家能发现什么特征？

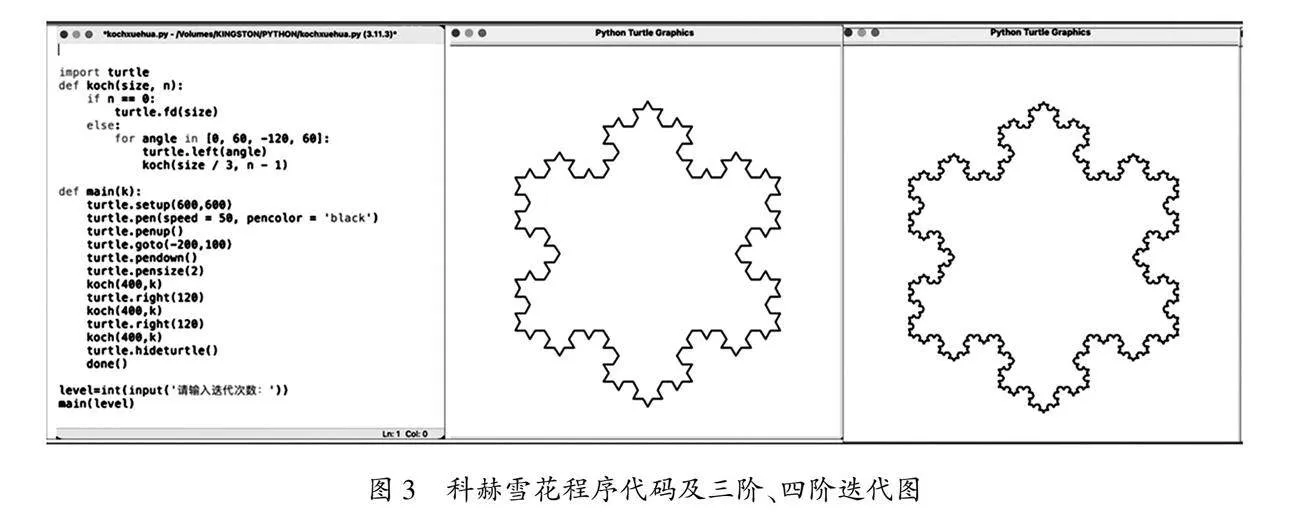
师生活动：教师展示学生编写的程序代码（图3）.通过多次迭代操作，引导学生直观感知科赫雪花曲线面积有限但周长无限的特点.

设计意图 该环节指向学生算法与协作思维的培养，通过技术、工程等学科的融入，增添学生的课堂参与度.学生不仅拓展了多学科的知识，更重要的是通过编制的程序能直观发现雪花曲线的特征.

4.3.3 发现规律，解释论证

问题4：如何用数学方法证明科赫雪花面积有限但周长无限的特点？

师生活动：教师和学生统一数据对雪花曲线进行定量分析：原三角形边长为a，周长为l，面积为s.让学生合作填写表1，尝试用数列知识得出雪花曲线周长和面积的通项公式，并用极限思想加以证明.

问题5：1967年，法国数学家曼德勃罗提出“英国海岸线有多长”的问题，并指出英国海岸线根本没有准确长度.你能否用刚刚探究雪花曲线得到的结论来支持这个说法？

师生活动：教师呈现海岸线图，并让学生小组讨论分析曼德勃罗说法背后的理由.事实上，由于海岸线极不规则，倘若用单位为千米的工具测量，那么几米到几百米的弯曲就可能被忽略不计；但改用单位为米的工具测量，则上述被忽略不计的弯曲可被计入，但仍然有几厘米到几十厘米的弯曲可能被忽略.可见，随着计量单位的不断缩小，海岸线测量值会不断变大.

问题6：分形为何有这种奇怪的特性，究竟何为分形？

师生活动：教师播放分形几何诞生的视频：分形几何由曼德勃罗首次提出，它是以非规则几何形态为研究对象的几何学.其基本思想是客观事物的局部与整体在形态、时间、空间等方面具有相似性.现实生活中广泛存在不规则形状和现象，因此分形几何已经成为重要的数学模型.

设计意图 数学需要严谨论证，通过数列知识与极限思想让学生对分形图形特征加以证明，在过程中学生数学运算、逻辑推理素养得到提升.通过小组合作探讨海岸线长度问题，有效地培养学生的问题解决能力.通过分形几何的介绍，让学生意识到分形几何比欧氏几何有更广泛的现实应用需求，从而提升批判思维能力.

4.3.4 知识迁移，深度感知

问题7：大自然中的分形以及科赫雪花曲线都让我们看到了分形的艺术之美.那在艺术家眼里，分形是否能够带来创作的灵感呢？

师生活动：教师呈现关于分形的美术作品，如《富士山景》《富春山居图》等.教师介绍这些作品中呈现的分形美，让学生鉴赏这些艺术作品.分形简单的自相似性，往往能够带给艺术作品精美的有序结构，让作品充满动态平衡，体现出数学中无穷的和谐.随后教师呈现装饰物上的分形纹理（图4）.

问题8：装饰物中出现了另一个典型的分形图形——谢尔宾斯基三角形，它与中国古代数学的杨辉三角形密切相关.当我们把杨辉三角中的奇数位标黑就能得到谢尔宾斯基三角形（图5左），你能发现这个三角形哪些特征？

师生活动：结合刚刚雪花曲线的分析方式，让学生思考谢尔宾斯基三角形的构造过程，并用数列的知识表示黑色部分的周长与面积.

问题9：如果是连接三边的垂足点，则可以得到谢尔宾斯基踏板三角形（图5右）.从数学角度看，你又能发现它有什么性质？

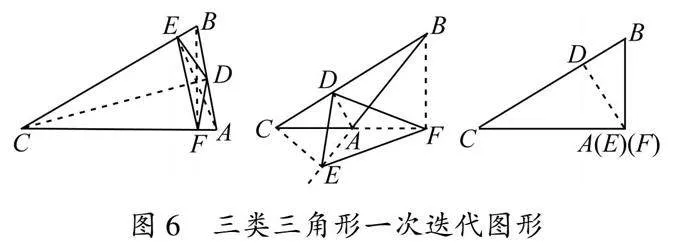
师生活动：教师引导学生对原三角形进行分类，从一次迭代出发，观察踏板三角形的性质（图6）.以锐角三角形为例，学生合作讨论可以得到原三角形和外围三个小三角形相似的结论.教师继续引导学生探究其他三角形是否具有同样性质.如果有，那么继续迭代下去，相似三角形的总个数是否可以用数列表示.

设计意图 通过介绍分形在艺术中的应用，在增添本堂课趣味的同时让学生感知到分形几何的魅力.由艺术引出谢尔宾斯基三角形，在探究雪花曲线后让学生自主探究谢尔宾斯基三角形，有利于提升知识迁移能力.

4.3.5 评价检测，反思总结

任务2：经过多个分形图形的学习，请小组合作完成一个分形艺术作品.

问题10：通过这堂课，你学到了什么？课后你还想对分形深入了解什么内容？

师生活动：教师指导学生合作完成艺术作品.可以引导学生从数学的角度加以设计，例如勾股树的分形.各小组分别上台展示作品，并阐述设计理念及作品中的分形元素.由学生本人、同学、教师对学生学习过程中任务或作品的完成情况进行多方面的量化及质性评估.最后师生共同回顾本次课的学习内容.

设计意图 学生合作完成分形艺术作品的过程中能有效培养学生创造力与协作能力.通过课堂反思总结，深化学生对分形的理解，同时激发进一步探索分形的兴趣.

5 结语

党的二十大报告中首次写入“推进教育现代化”，并明确要求着力提升师生数字化素养和能力.在此背景下，培养学生与数智时代相匹配的素养已成为新时代教育的重要议题.STEAM教育与计算思维的融合为计算思维融入基础学科教育提供了可行路径.数学与诸多学科均有联系，且与计算思维内涵具有高度一致性.以数学为主导的STEAM+CT教学能够将不同学科建立有机衔接，教学过程能够有效指向计算思维核心能力的培养.这不仅回应了计算思维融入中小学教育的时代号召，同时回应了数学课程倡导跨学科教学的现实需求.本研究提出的教学实施框架为STEAM+CT教学提供新路径，以期实现STEAM+CT教学和数学课程之间的协同增益.未来需要进一步丰富这一路径的内涵与形式，为STEAM+CT教学提供借鉴.

参考文献

［1］Mills K， Coenraad M， Ruiz P， et al. Computational thinking for an inclusive world： a resource for educators to learn and lead［R］. Digital Promise， 2021.

［2］Bocconi S， Chioccariello A， Kampylis P， et al. Reviewing Computational Thinking in Compulsory Education［R］. Joint Research Centre （Seville site）， 2022.

［3］Wing J M. Computational thinking［J］. Communications of the ACM， 2006， 49（03）： 33-35.

［4］CSTA & ISTE. Operational Definition of Computational Thinking for K-12 Education. ［DB/OL］.［2012-04-15］. http：//csta.acm.org/Curriculum/sub/CurrFiles/CompThinkingFlyer.pdf.

［5］王罗那，王建磐.人工智能时代需要关注的新素养：计算思维［J］.比较教育研究，2021，43（03）：24-30+38.

［6］胡焱，蒋秋.数学教育与STEM（STEAM）教育的融合：机遇与挑战——基于数学教育与STEM（STEAM）教育国际学术研讨会［J］.数学教育学报，2019，28（06）：92-94.

［7］Shute V J， Sun C， Asbell-Clarke J. Demystifying computational thinking［J］. Educational research review， 2017， 22： 142-158.

［8］Costa E J F， Campos L M R S， Guerrero D D S. Computational thinking in mathematics education： A joint approach to encourage problem-solving ability［C］//2017 IEEE Frontiers in Education Conference （FIE）. IEEE， 2017： 1-8.

［9］蔡金法，徐斌艳.也论数学核心素养及其构建［J］.全球教育展望，2016，45（11）：3-12.

［10］刘锦，曹一鸣.计算思维对中学数学课程改革的启示［J］.数学通报，2021，60（10）：13-15+42.

［11］Korkmaz ， akir R， zden M Y. A validity and reliability study of the computational thinking scales （CTS）［J］. Computers in human behavior， 2017， 72： 558-569.

作者简介

刘宁晖（1999—），男，浙江宁波人，浙江师范大学硕士研究生; 主要研究方向为数学学科教学.

朱哲（1979—），男，浙江绍兴人，教育学博士，浙江师范大学副教授，硕士生导师;主要研究方向为数学课程与教学论、数学史与数学教育研究.