运用乘法分配律进行简算

同学们，乘法分配律能帮助我们进行简便运算，提高运算速度。乘法分配律就是当相加的两个数与一个数相乘时，可以把这两个数分别与这个数相乘，再把两个积相加，所得的结果不变。用字母表示是（a+b）×c=a×c+b×c。有时我们可能会遇到相减的两个数与一个数相乘的情况，性质类似，用字母表示为（a-b）×c=a×c-b×c。

不过，只记住用字母表示的乘法分配律还不够，还得会根据算式的特点进行灵活运用。而运用乘法分配律的关键是“凑整”。下面我们就结合实例一起来看看如何运用乘法分配律进行简算吧。

1.直接运用计算

遇到（a+b）×c或（a-b）×c的情况时，如果a×c和b×c都比较简便，就可以直接用a×c+b×c或a×c-b×c计算。如：

2.逆向运用计算

遇到a×c+b×c或a×c-b×c的情况时，如果（a+b）或者（a-b）是一个整十、整百的数，就可以用（a+b）×c或（a-b）×c来计算。如：

3.拆加、拆减后运D39FGAi4m9aZ9HX+kyQibg==用计算

两个数相乘，把其中一个接近整十、整百的数改写成整十、整百的数与一个数相加或相减，再运用乘法分配律进行计算。

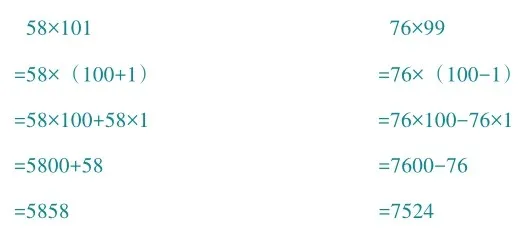
4.变式后逆用计算

有些算式表面上看不符合逆向运用公式计算的标准形式，但经过变式后，就能逆用公式进行简算了。

5.转化后运用（逆用）计算

有些算式表面上看虽然不能用乘法分配律简算，但根据算式中数的特点，可以转化为能用乘法分配律简算的标准形式（或逆向运用的标准形式）进行计算。