基于SLSTM模型的公路货运智能预测研究

摘要 针对公路货运预测问题，提出一种季节预处理技术，并结合长短期记忆网络模型（long-short term memory，LSTM）构建SLSTM智能预测模型。以江西省季度公路货运量和货运周转量为例，与持续模型、灰色模型、自回归模型、LSTM模型相比，提出的SLSTM模型能够有效降低预测误差约40.2%～74.4%，旨在为公路交通规划提供一定参考。

关键词 公路货运；深度学习；季节预处理；智能预测

中图分类号 U491 文献标识码 A 文章编号 2096-8949（2024）18-0001-03

0 引言

公路货运预测是指在市场调研基础之上预测未来一段时间公路货运量和货运周转量的变化情况，它不仅有利于企业发挥市场作用、助力企业制定经营目标和决策、强化企业管理、提升企业经济效益，而且是公路交通基础设施建设的基础，对于交通运输规划管理具有重要指导意义。

张晓延等[1]采用灰色模型（grey model，GM）针对港口的货运量进行了预测，并分析了运河效益。常志宏等[2]利用皮尔逊相关系数分析了公路货运量的影响因素，构建各影响因素与公路货运量之间的非线性回归预测模型。张婷[3]采用指数平滑法预测了西安市地铁客运量的市场份额。张楠等[4]利用回归模型和弹性系数法，建立了货运量和GDP之间的关系，以实现京杭运河货运量的预测。类似地，王寅生[5]建立了铁路客货运量与GDP的三次多项式关系式，基于此预测未来的客货运量。秦孝敏[6]和李逸飞等[7]分别探讨了川渝东出铁路货运量和苏州北站客运量的预测情况。马周等[8]先利用GM模型预测客货运量，然后基于弹性系数法建立客货运量与GDP之间的预测解析式，最后对二者取平均。随着人工智能算法的发展，大量学者利用深度学习算法开展了深度学习智能预测研究[9]。康家明[10]先利用灰色预测模型进行初步预测，然后引入长短期记忆网络模型（long-short term memory，LSTM）预测残差序列，由此构建了组合预测方法，相比单一模型通常具有更佳的预测性能。

综上，已有研究大多是针对年度客货运量，鲜有研究分析客货运量的季度特征并展开预测。该文针对公路货运预测问题，提出了一种季节预处理技术，然后结合归一化处理和LSTM模型，构建了SLSTM组合预测模型，可为公路交通规划提供及时指导。

1 理论方法

1.1 公路货运智能预测流程

该文提出的公路货运SLSTM智能预测模型主要包括3步：

（1）统计季度公路货运量和货运周转量，引入季节预处理技术，考虑季节周期特征和整体发展趋势，针对各季度分别建立线性模型，然后进行去均值、归一化处理，得到预处理序列。

（2）针对预处理序列建立LSTM模型，确定模型的超参数，并进行序列智能预测。

（3）将预处理序列的智能预测结果反算得到季度公路货运量和货运周转量的预测值。

1.2 季节预处理技术

1.3 LSTM模型

1.4 误差评估指标

2 江西省公路货运量和货运周转量预测

2.1 统计数据分析

该文以2019年1季度～2024年1季度的江西省公路货运量和货运周转量为例，绘制其季度趋势如图1所示。数据的前18组为训练集，用于建立预测模型，后3组为测试集，用于验证预测模型的精度。

2.2 预测模型定义

为全面评估预测模型的性能，将其与持续模型（persistence model，PM）、GM模型、自回归模型（autoregressive，AR）、LSTM模型进行对比。

2.3 公路货运量预测分析

2.3.1 预测结果

各模型季度公路货运量预测结果如图2所示。可以发现，GM和LSTM均未预测出其公路货运量的变化趋势，这是因为这两种模型难以将季节性因素考虑在内。而PM、AR、SLSTM模型能一定程度预测其变化趋势，其中PM模型预测结果整体偏低。因为此处的PM模型采用了往年同季度的值作为预测值，一定程度考虑了季节周期性，但同时忽略了季节增长趋势。AR模型选用了8阶，将前两年的数据均考虑在内，有效捕捉了数据的季节周期性。从时程序列来看，提出的SLSTM模型与实际值最吻合。

2.3.2 误差分析

为量化评估各模型的预测精度，绘制季度公路货运量预测误差柱状图如图3所示。可以看出，GM和LSTM模型的效果较差，而PM、AR、SLSTM模型的精度较高。以PM模型为基准，AR和SLSTM模型的MAE误差分别降低了16.4%和74.4%，RMSE误差分别降低了-6.0%和70.0%。整体而言，该文提出的SLSTM预测精度最高，MAPE误差为1.8%。

2.4 公路货运周转量预测分析

2.4.1 预测结果

各模型季度公路货运周转量的预测结果如图4所示。与公路货运量类似，PM、AR、SLSTM模型的预测性能较好，该文提出的SLSTM模型预测结果与实测最接近。

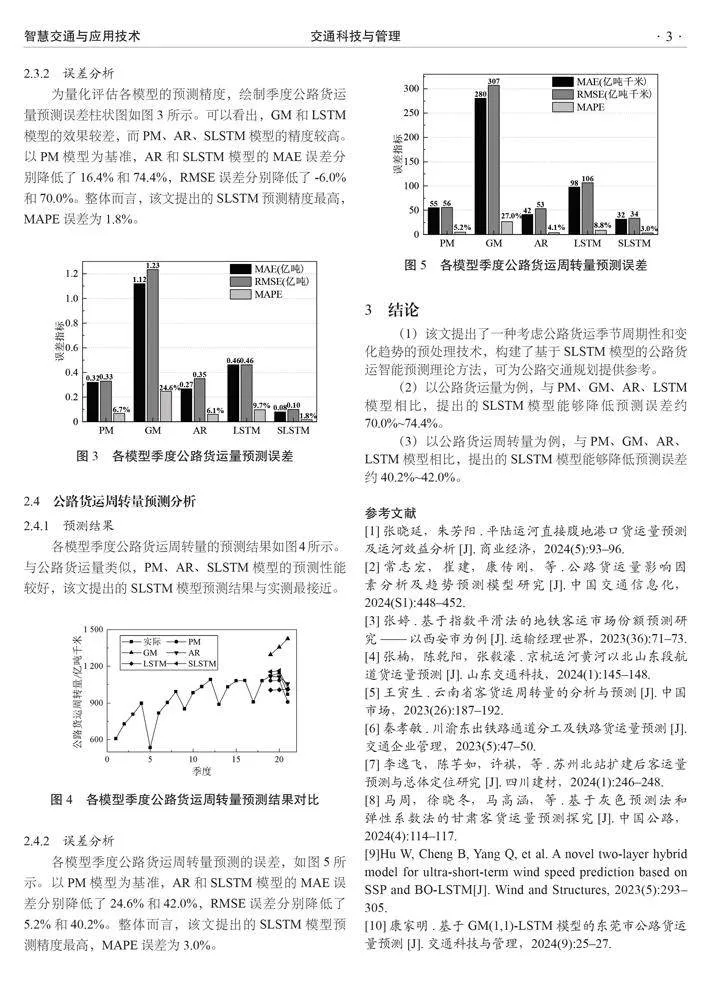
2.4.2 误差分析

各模型季度公路货运周转量预测的误差，如图5所示。以PM模型为基准，AR和SLSTM模型的MAE误差分别降低了24.6%和42.0%，RMSE误差分别降低了5.2%和40.2%。整体而言，该文提出的SLSTM模型预测精度最高，MAPE误差为3.0%。

3 结论

（1）该文提出了一种考虑公路货运季节周期性和变化趋势的预处理技术，构建了基于SLSTM模型的公路货运智能预测理论方法，可为公路交通规划提供参考。

（2）以公路货运量为例，与PM、GM、AR、LSTM模型相比，提出的SLSTM模型能够降低预测误差约70.0%～74.4%。

（3）以公路货运周转量为例，与PM、GM、AR、LSTM模型相比，提出的SLSTM模型能够降低预测误差约40.2%～42.0%。

参考文献

[1]张晓延，朱芳阳.平陆运河直接腹地港口货运量预测及运河效益分析[J].商业经济，2024（5）：93–96.

[2]常志宏，崔建，康传刚，等.公路货运量影响因素分析及趋势预测模型研究[J].中国交通信息化，2024（S1）：448–452.

[3]张婷.基于指数平滑法的地铁客运市场份额预测研究——以西安市为例[J].运输经理世界，2023（36）：71–73.

[4]张楠，陈乾阳，张毅濠.京杭运河黄河以北山东段航道货运量预测[J].山东交通科技，2024（1）：145–148.

[5]王寅生.云南省客货运周转量的分析与预测[J].中国市场，2023（26）：187–192.

[6]秦孝敏.川渝东出铁路通道分工及铁路货运量预测[J].交通企业管理，2023（5）：47–50.

[7]李逸飞，陈芋如，许祺，等.苏州北站扩建后客运量预测与总体定位研究[J].四川建材，2024（1）：246–248.

[8]马周，徐晓冬，马高涵，等.基于灰色预测法和弹性系数法的甘肃客货运量预测探究[J].中国公路，2024（4）：114–117.

[9]Hu W， Cheng B， Yang Q， et al. A novel two-layer hybrid model for ultra-short-term wind speed prediction based on SSP and BO-LSTM[J]. Wind and Structures， 2023（5）：293–305.

[10]康家明.基于GM（1，1）-LSTM模型的东莞市公路货运量预测[J].交通科技与管理，2024（9）：25–27.