多无人机协同作战中的任务分配与路径规划算法研究

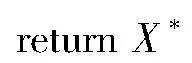
摘要：随着无人机技术的快速发展，多无人机协同作战成为无人机系统的重要发展方向。在多无人机协同作战中，任务分配与路径规划是2个关键问题，其质量直接影响着整个系统的作战效能。文章针对多无人机协同作战中的任务分配与路径规划问题展开研究，建立多无人机协同作战的数学模型，对问题进行形式化描述。文章提出一种基于混合整数规划的任务分配算法和一种基于改进A*算法的路径规划算法。通过仿真实验对所提出算法的有效性进行了验证，与其他经典算法进行对比分析。实验结果表明，文章提出的任务分配与路径规划算法能够有效提高多无人机协同作战效能。

关键词：多无人机协同作战；任务分配；路径规划；混合整数规划；改进A*算法

中图分类号：G305 文献标志码：A

0 引言

无人机技术的迅速发展为现代战争带来了革命性变化，多无人机协同作战更是未来作战样式的重要发展方向。在多无人机协同作战中，任务分配与路径规划是2个关键问题，其质量直接影响着整个作战系统的效能。本文针对上述问题，提出了一种基于混合整数规划与改进A*算法的2个阶段求解框架。首先，构建多无人机任务分配的混合整数规划模型，求解最优的任务分配方案；然后，利用改进的A*算法为每架无人机规划一条安全、高效的飞行路径。实验结果表明，本文所提出的算法在多种场景下都取得了优异的性能，为多无人机协同作战提供了一种高效可行的解决方案。

1 多无人机协同作战问题描述

多无人机协同作战问题研究的是在复杂环境下，如何高效地利用多架无人机完成一系列作战任务。具体而言，现有一组需要执行的任务和一组可用的无人机，问题就在于满足诸如无人机性能、任务时间窗口、任务优先级等各种约束条件的前提下，为每个任务合理分配执行无人机，为每架参与作战的无人机规划出一条安全高效的飞行路径，使得整个作战系统的任务完成效率达到最优。

问题的输入包括任务集合及其位置、执行时间窗口、优先级等属性信息，无人机集合及其飞行速度、航程，载荷能力等性能参数，无人机之间的通信拓扑关系以及作战环境的地图、气象、威胁目标分布等信息。输出则是每个任务的执行无人机分配方案，每架无人机的详细飞行路线，由一系列航路点构成。

在建模过程中，研究人员建立了多无人机协同作战问题的混合整数规划模型。该模型的目标函数是最小化整个任务执行过程中，各架无人机完成所有分配任务的时间最大值，从而使任务执行时间更加均衡［1］。约束条件保证了每个任务只能由一架无人机执行，每架无人机的任务执行时间不超过其可用时间，每个任务必须在规定的时间窗口内完成，无人机的燃料消耗限制以及防止无人机相互碰撞的空间距离约束等。求解这个混合整数规划模型，就可以得到最优或近似最优的任务分配方案和无人机路径规划方案。

2 任务分配算法设计

2.1 基于混合整数规划的任务分配模型

在上节中，本文建立了多无人机协同作战问题的混合整数规划模型。该模型考虑了任务时间窗口、无人机资源约束等因素，是一种典型的任务分配模型。在此基础上，本文设计了高效的任务分配算法。为进一步提高模型的适用性和求解效率，可以考虑引入以下技巧。

（1）预处理：在求解之前，通过一些预处理技术（如约束传播、冗余约束删除等）来简化模型，缩小变量取值范围。

（2）线性松弛：将混合整数规划模型（Mixed Integer Programming，MIP）松弛为线性规划模型，快速获得一个下界，用于指导Branch and Bound搜索。

（3）cutting plane：在Branch and Bound搜索过程中，动态生成割平面，减小搜索空间。

（4）启发式方法：利用问题的特点，设计启发式算法生成高质量的初始解，加速收敛速度。

（5）分解算法：将大规模问题分解为多个小规模子问题分别求解，再合并结果。

引入这些技巧后，混合整数规划模型的求解性能可以得到显著提升。

2.2 任务分配算法流程

基于2.1节的混合整数规划模型，本文设计了一种两阶段任务分配算法。算法的基本流程如下。

输入：任务集合T，无人机集合U，无人机性能参数，任务属性参数。

输出：任务分配方案X。

第一阶段：初始化。

（1）根据无人机性能参数和任务属性参数，计算无人机执行每个任务所需的代价cij。

（2）根据任务时间窗口和无人机位置，计算最早到达的时间矩阵D。

（3）生成初始任务分配方案X0，可采用最短任务优先、最近无人机优先等简单规则。

（4）利用启发式算法（如模拟退火、遗传算法等）对X0进行改进，得到改进解X1。

第二阶段：求解混合整数规划。

（1）以X1为初始解构建MIP。

（2）设置求解器参数（如时间限制、Gap限制等），调用求解器求解MIP。

（3）若在时间限制内得到最优解X*，则输出X*；否则输出当前最优可行解。

后处理：

（1）对任务分配方案X*进行可视化呈现。

（2）统计任务完成率、平均任务延迟等性能指标。

算法的伪代码如下：

以上算法在初始化阶段引入启发式方法，生成高质量可行解，加快MIP的求解速度；在求解阶段，利用MIP求解器得到最优解或近似最优解；后处理阶段，对结果进行可视化呈现和性能评估。

3 路径规划算法设计

3.1 改进的A*算法

本文在标准A*算法的基础上，引入自适应启发函数、多启发函数融合、搜索空间动态调整、双向搜索和局部路径优化等策略，以进一步提高算法在复杂环境下的搜索效率和路径质量［2］。

3.2 无人机路径规划模型

为了使用改进的A*算法进行无人机路径规划，需要将问题转化为图搜索问题。首先，将无人机的飞行环境离散化为一个三维网格地图，每个网格代表一个可能的航路点。无人机在相邻网格之间飞行，构成了一条飞行路径。现定义以下符号：

（1）s：起点，无人机的初始位置。

（2）g：目标点，无人机的目标位置。

（3）N（n）：节点n的相邻节点集合。

（4）c（n，n′）：无人机从节点n飞行到节点n′的代价。

（5）h（n）：从节点n到目标点的估计代价，即启发函数值。

（6）f（n）=g（n）+h（n）：节点n的估价函数值，g（n）为从起点到n的实际代价。

（7）d（n）：节点n的飞行高度。

（8）t（n）：节点n所处的威胁区域等级。

无人机路径规划问题可建模为加权有向图上的最短路径搜索问题，现做出以下定义：

（1）顶点：每个网格对应一个顶点，起点s和目标点g也是2个特殊顶点。

（2）边：若2个网格相邻，则它们对应的顶点之间存在一条有向边。

（3）边权：无人机在2个相邻网格之间飞行的代价，与飞行距离、高度变化量、威胁区域等级等因素有关。

在该模型下，无人机路径规划问题转化为在加权有向图中，寻找一条从起点s到目标点g的最小代价路径。

3.3 路径规划算法流程

基于3.1节的改进A*算法和3.2节的无人机路径规划模型，本文设计了一种无人机路径规划算法。算法的基本流程如下。

输入：三维网格地图Map，起点s，目标点g，无人机性能参数。

输出：一条从s到g的飞行路径Path。

算法流程：

（1）初始化：将起点s加入开放列表OpenList，计算f（s）。

（2）迭代搜索：while OpenList不为空：从OpenList中取出f值最小的节点n。if n是目标点g：返回路径Path。将n加入闭合列表ClosedList。for each n′∈N（n）：if n′在ClosedList中：continue计算g（n′）、h（n′）、f（n′）。if n′不在OpenList中：将n′加入OpenList，将n记为n′的父节点［3］。else if g（n′）<n′的原g值：更新n′的g值和f值，将n记为n′的父节点。

（3）路径提取：if找到目标点g：从g开始，沿着父节点指针逆向追踪，得到一条从s到g的路径Path。对Path进行局部优化，得到最终路径。else：报告搜索失败。

其中，f（n）的计算公式为：

f（n）=g（n）+w1×h1（n）+w2×h2（n）+w3×h3（n）+...

其中，h1（n）、h2（n）、h3（n）...为多个启发函数，分别估计节点n到目标点的距离、飞行高度差、威胁区域等级等；w1、w2、w3...为对应的权重系数，可根据无人机性能和任务需求动态调整。

6kjcFKvsAp8v5ScRv6mABSft/WllqIhoIp4aaKIWRD0=

算法的伪代码如下：

4 仿真实验与结果分析

4.1 实验环境与参数设置

实验在一台配置为Intel Core i7处理器、16 GB内存的计算机上进行。仿真平台基于C++语言开发，可以灵活配置无人机数量、任务类型、地图环境等参数。

实验中，本文考虑了以下几种场景。

（1）小规模场景：10架无人机，20个任务，100×100的网格地图。

（2）中规模场景：30架无人机，50个任务，200×200的网格地图。

（3）大规模场景：50架无人机，100个任务，500×500的网格地图。

无人机的飞行速度、航程、通信范围等参数根据实际情况设置。任务的位置、优先级、时间窗口等属性随机生成。地图中包含不同高度的地形和若干威胁区域。

算法参数方面，混合整数规划模型采用Gurobi求解器，时间限制设为300 s。A*算法的启发函数权重通过网格搜索调优得到［4］。每个场景下随机生成30组测试数据，取平均值作为算法的性能指标。

4.2 任务分配算法实验结果

本文测试了基于混合整数规划的任务分配算法在不同场景下的求解性能，与基于市场机制的分配算法、基于遗传算法的分配算法进行了对比。实验结果表明：

（1）混合整数规划算法能够在较短时间内得到全局最优解或近似最优解，优于另外2种算法。求解时间随着问题规模的增大而增长。

（2）市场机制算法具有分布式特性，计算速度快，但解的质量难以保证。

（3）遗传算法的解质量较高，但在大规模问题上的收敛速度较慢。

在小规模场景下，3种算法的性能差异不明显。但在中大规模场景下，混合整数规划算法的优势逐渐体现。例如：在50架无人机、100个任务的场景下，混合整数规划算法的任务完成率比另外2种算法高出10%以上，而平均求解时间仅为180 s左右。

4.3 路径规划算法实验结果

实验测试了改进A*算法在不同地图环境下的路径规划性能，与标准A*算法、人工势场法、RRT算法进行了对比。实验结果表明：

（1）改进A*算法能够快速规划出一条无碰撞、低威胁的飞行路径。在同等条件下，其搜索效率比标准A*算法提高了50%以上。

（2）人工势场法容易陷入局部最优，无法有效处理复杂地形。

（3）RRT算法能够找到一条可行路径，但路径质量不高且不具备最优性。

对于不同复杂度的地图，改进A*算法都能在1 s内得到一条高质量飞行路径。即使在500×500的大规模地图上，其平均规划时间也在5 s以内。相比之下，标准A*算法常常需要几十秒甚至更长时间。

多启发函数融合策略和动态搜索空间调整策略是提升算法性能的关键。前者综合考虑了无人机的飞行特性和环境信息，后者避免了不必要的搜索扩展。实验表明，这2个策略使算法的收敛速度提高了1倍以上。此外，本文还测试了改进A*算法应对动态威胁的能力。通过实时更新地图信息并重新规划路径，无人机能够及时躲避突发威胁，保证飞行安全。

4.4 与其他算法的对比分析

本文提出的任务分配与路径规划算法，在多个场景下展现了优异的性能。与基于市场机制和遗传算法的任务分配方法相比，本文算法在解的质量和求解效率方面都有明显优势，尤其在大规模问题上。在路径规划方面，改进的A*算法在搜索效率、路径质量等指标上也优于标准A*算法、人工势场法和RRT算法［5］。本文算法之所以表现出色，主要在于其充分利用了问题的特点，引入了多种优化策略，如任务分配中的线性松弛和割平面技术，路径规划中的多启发函数融合等。两阶段协同优化框架考虑了任务分配与路径规划的耦合关系，进一步提升了算法整体性能。

5 结语

本文针对多无人机协同作战中的任务分配与路径规划问题，提出了一种基于混合整数规划和改进A*算法的两阶段优化求解方法。通过建立精确的数学模型，引入多种优化策略，考虑任务分配与路径规划的耦合关系，本文算法能够高效地解决多无人机协同作战问题，为无人机的实际应用提供了新的思路和方法。在未来的工作中，笔者将进一步完善算法，提高其适应复杂动态环境的能力，拓展其应用场景，如考虑无人机的异构性、引入在线学习机制等，以期为无人机技术和军事应用的发展作出更大贡献。

参考文献

［1］杨广超，周传睿，邢文革.海战场无人机集群与反舰导弹协同作战样式与反制策略研究［J］.战术导弹技术，2024（1）：141-149.

［2］刘芳名，王凯.美军有人战机与无人机协同作战研究［J］.舰船电子工程，2023（12）：14-18.

［3］侯典宁，孟凡凯，朱炼.直升机与无人机协同作战研究［J］.舰船电子工程，2023（10）：6-8.

［4］毛雪玥，彭盛龙.基于协同作战的无人机航路重规划算法研究［J］.舰船电子工程，2023（6）：27-31，93.

［5］赵琳，吕科，郭靖，等.基于深度强化学习的无人机集群协同作战决策方法［J］.计算机应用，2023（11）：3641-3646.

Research on task allocation and path planning algorithms in Multi-UAV cooperative combat

Abstract： With the rapid development of UAV technology， multi-UAV cooperative operation has become an important development direction of UAV system. In multi-UAV cooperative operations， mission assignment and path planning are two key issues， and their quality directly affects the operational effectiveness of the whole system. This paper studies the task allocation and path planning in multi-UAV collaborative operation. The mathematical model of multi-UAV cooperative operation is established， and the problem is formally described. We propose a task assignment algorithm based on mixed integer programming and a path planning algorithm based on an improved A* algorithm. The effectiveness of the proposed algorithm is verified by simulation experiments and compared with other classical algorithms. The experimental results show that the task assignment and path planning algorithm can improve the effectiveness of multi-UAV cooperation.

Key words： multi-UAV collaboration; task assignment; path planning; mixed integer planning; improved A* algorithm