用好学生经验 促进数学理解

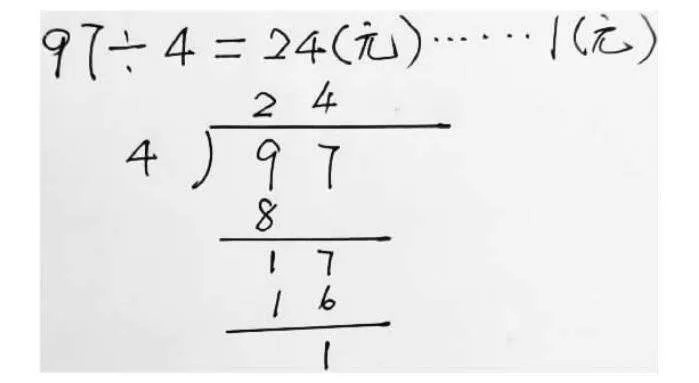
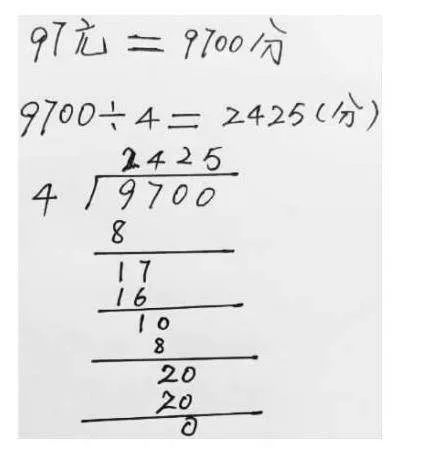
学生经验是正在进行的新课改中的一个重要术语，在《义务教育国家课程方案（2022年版）》和《义务教育数学课程标准（2022年版）》中多次提到。按照对数学课程标准的理解及对数学教学的实践解读，学生经验主要指向学生的生活现实、数学现实和其他学科现实，它包含学生已有的知识经验和认知加工水平（思维水平）经验。新课改强调学生的数学学习应建立在学生已有的基础之上进行，教学设计、素材选取、情景创设等都要贴近学生现实和认知加工水平，“以利于学生经历从现实情景中抽象出数学知识与方法的过程、发展抽象能力、推理能力等”。

在数学课堂教学中用好学生经验，能更好地凸显学生学习的主体地位，建立学习中心课堂，落实学生的深度学习，促进学生对数学的理解，发展学生的学科核心素养。

一、联结生活经验，促进数学理解

“数学是源于现实世界的抽象。”小学数学内容更能直观地反映数学与现实世界的联系，小学生对数学的理解与掌握离不开生活经验的支撑。教学中应选取贴近学生生活现实的素材，创设“真实情景”，让学生在“熟悉的实物，以及自然、社会的现象和问题”中追溯和建构数学的“真实原型”，依托这可具体感知“原型”，理解数学知识，习得数学方法、解决数学问题，感悟数学思想、积累数学基本活动经验。

如，教学“小数除法”，创设现实情景问题：有4位朋友一起吃饭，一共吃掉97元。每人应付多少钱？（AA制）

学生先独立解决这个问题，有学生得到这样有余数的结果：

面对这个真实的情景，用以前“有余数的除法”知识解答，答案是24元余1元。问题就来了：是24元，还是25元？这个AA制问题引发了学生新的认知冲突，也催发了学生寻求正确答案的强烈愿望，推动学生进行更深度的互动交流。基于现实经验和计算验证，每个人应付的钱肯定大于24元，而小于25元。学生聚焦“余下的1元怎么分”进行了深度的交流，最终获得了一种合理解释且实际可以进行的操作：余下的1元就是10角，10角平均分成4份，每人分到2角，还剩下2角；同样的道理，这剩下的2角就是20分，20分再平均分成4份，每人分得5分钱。所以1元平均分给4个人，每人就是2角5分，化成单位“元”就是0.25元，最终每人应付24.25元。

也有学生想到利用元角分之间的进率转化关系得到这样的结果：

显然，这样的思考同样出自学生对“钱”的生活理解，可以进一步帮助学生理解小数除法的算理或者说对前者“说法”的有效验证。

以上两种解释为经验基础，结合十进制位值原理，联系整数除法、小数的意义，进而再对数进行计算。在教师的点拨指导下学生认识到可以把整数1看作10个0.1，再用10个0.1除以4，每份分得2个0.1，即0.2。余下的0.2又可以看作20个0.01，再用20个0.01除以4，每份分的5个0.01。最终编制出小数除法竖式计算程序，建构出小数除法竖式计算模型：

上面的案例中，“理解算理，掌握算法”属于“基本技能”，“小数除法怎样除，小数点怎样处理，为什么这样算？”一般的老师会用“直接告诉”的方式“传递”给学生，但优秀的教学不是简单地“告诉”，而是引领学生进入“现实情景”，引发认知冲突，助推学生生活现实经验与数学的联结，让学生结合生活现实理解，努力“说理”，经历算法的产生过程，从中理解算理，抽象算法，在习得知识、方法的同时获得数学核心素养的发展。

二、沟通数学现实，促进数学理解

小学数学教材内容是按“螺旋上升”的方式编排的，随着数学学习的不断深入，学生所积累的数学基本知识和方法，具备的数学基本技能和活动经验也就越丰富、越厚实，这些数学现实是学生后续学习数学的素材，为学生进一步学习数学奠定了经验基础。对原有数学知识、方法的考查、分析、反思，沟通相关联的知识和方法之间的内在联系，找出“同质点”，通过归纳概括，推理“发现”并建构出一类问题的解决方法或原理应是数学学习的一种重要思维方式，也是促进数学理解、数学思维进阶的重要途径。

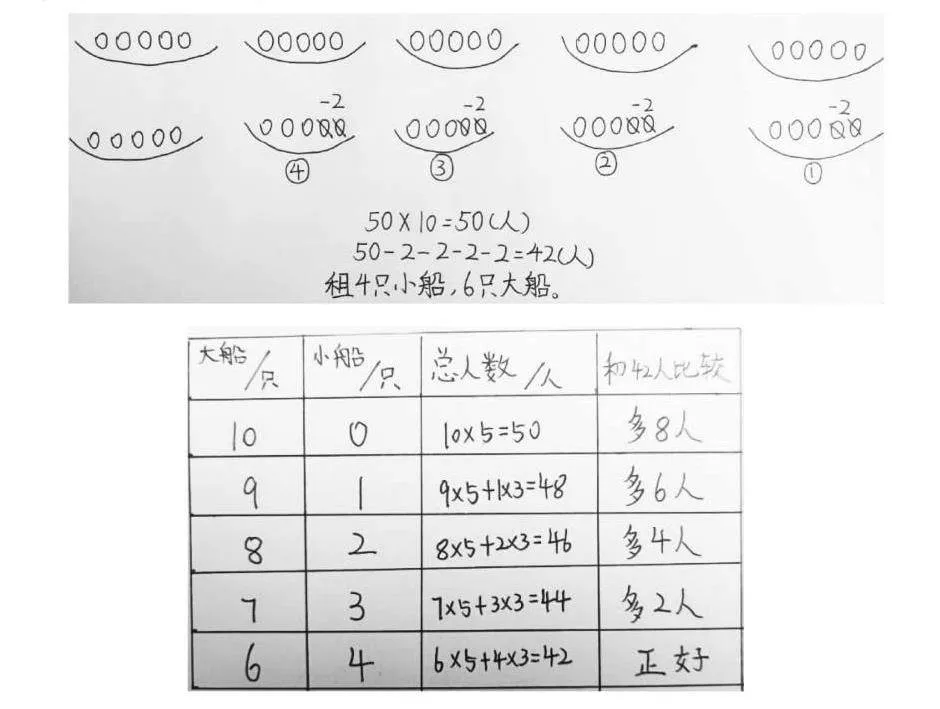
如，教学“租船问题”：全班42人去公园划船，租10只船正好坐满。每只大船坐5人，每只小船坐3人。租的大船、小船各有多少只？

当学生用“画图”和“列表”的方法，运用“一一列举”策略解答后，老师选择学生的画图法和列举法同时重新并排展示在大屏幕上，进一步提出要求：“我们一起再来观察、比较这两种不同的解题策略，特别是认真分析他们的思考过程，有没有什么异曲同工之处？”

学生展开了更有深度互动的交流，逐渐将数学的眼光聚焦于“人数变化”上，将思维落在“变化规律”上：

“不管是画图思考还是列表一一列举尝试寻找，每次调整前都要和总人数进行比较，每次都是减少2人。”

“把一只大船换成一只小船就可以少坐2人。要少坐8人，只要把4只大船换成4只小船就可以了，列式是8÷2=4，算出来的就是要租小船的只数。最后10-4=6，就算出了要租大船的只数。”

“老师，你说过学数学要学会想象，数学学习离不开计算。我发现，其实不管是画图还是一一列举，一开始都用到了假想和计算。我就用了假想和计算的方法。第一步我在脑海中先假想有10只大船，一共可以坐50人。第二步就和实际人数比较，发现多出8人。我就想怎样把这8人抵消掉呢？一只小船可以坐的人数比一只大船少2人，就只要把几只大船换成几只小船。8人是4个2人，脑海中就把4只大船换成4只小船，也就是算出了要租小船的只数是4只，大船就是6只。我是这样列式的：（5×10-42）÷（5-3）=4（只），10-4=6（只）。”

这是六年级下册第三单元“选择策略解决实际问题”的例题2，实质是鸡兔同笼问题的变式题。教材的教学目标定位是要求学生能选择“画图”或“列表”的方法，运用“一一列举”的策略来解决问题。课堂教学实践证明，这样的教学目标，学生基本都能达到。这对于即将小学毕业的六年级学生来说，显然没有难度，在数学思维上显得有点“低阶”，还停留在“浅层思维”的层面，通过“画图”或“列表”的方式来“一一列举”的方法并没有构建出解决“鸡兔同笼”这一类经典数学问题的数学模型。在课堂中，教师应该引导学生多走一步，更进一步，借助学生已有画图或列表的“列举”策略经验，把可视、显性的“列举过程”再次转化成学习的素材，组织、启发学生对“列举”过程进行再次观察，深度思考，在素材结构化的组织和呈现中，有意识地、适度地去培养、发展学生抽象思维、逻辑思维和推理能力，完成“假设法”的建构，助推学生对一类经典数学问题解决方法的本质理解和建模。

三、整合其他学科知识，促进数学理解

古人云：“它山之石可以攻玉。”数学学习不能只是“独善其身”“闭门思考”，小学丰富的学科课程使小学生的“跨学科学习”成为可能。在教学中，教师要努力打破学科界限，在各学科中寻找与数学的契合点、整合点，凝练数学学习主题，创设真实的问题情景、开发实践时空，让学生在各学科之间开展“纵横捭阖”，具身实践，综合运用数学和其他学科的知识与方法解决现实世界中的真实问题，通过真实问题的解决促进对数学知识的理解和运用，培养实践精神，发展核心素养。

如，封闭图形上的行程问题：甲、乙两人沿着400米的环形跑道跑步。他们同时从同一地点出发，同向而行。甲的速度是280米/分，乙的速度是240米/分。经过多少分钟甲第一次追上乙？

解决该类问题的关键是学生缺乏“甲第一次追上乙时的路程差是多少”的准确认知经验。显然，这和“匀速变化”的物理现象相关，也是和体育相关的问题。有心的老师便会和体育老师联合组织学生开展专项活动，让学生带着“真实问题”，用数学的眼光去观察运动中的“数学事实”，在学生亲历的学科实践活动中见证到“第一次相遇时，快速者总比慢速者多跑1圈”的事实规律。

【注：本文系无锡市教育科学“十四五”规划课题“以参与者经验为起点的小学课堂教学设计研究”（编号：B/XC/2023/10）的阶段性研究成果】