“曹冲称象的故事”第3课时教学建议

“曹冲称象的故事”第3课时是《义务教育数学课程标准（2022年版）》第二学段综合与实践主题活动2的教学内容，其教学难点是：理解曹冲称象中大象重量和石头重量相等的原理，找到中间量，从而体会等量的等量相等，培养学生的推理意识。教学中，教师要设计怎样的数学活动，帮助学生突破教学难点，培养学生的推理意识？

活动一：开门见山，提出问题

【片段一】

课一开始，教师出示前测单进行交流：

1. 在“曹冲称象”这个故事里，要得到大象的重量，为什么最后去秤石头的重量？怎么不直接称大象呢？

生：古代的秤能称量的最大值有限，无法直接称出一头大象的重量。

2. 按照曹冲这个方法称出来的石头重量和大象的重量相等吗？为什么？说一说你的理由？

生：两次称量都到了同一刻度线，所以大象的重量等于石头的重量。

评析：通过前测问题交流，我们了解到大部分学生都能够知道因为两次称量到了同一刻度线，所以大象的重量就等于石头的重量。但是为什么两次称重到了同一刻度线大象的重量就等于石头的重量呢？这是学生说不清楚道不明白的。那是因为在现实情境中很难体会排开水的重量即“中间量”，从而体会等量的等量相等，因此，需要教师将生活问题转化为数学问题进行研究，一开课就让学生明晰教学难点。

活动二：实验助力，突破教学难点

苏霍姆林斯基曾指出：“儿童的智慧在他的手指尖上。”由此可见，学生的思维离不开实践活动，只有学生自己根据等量的表象去探索实践发现代换的抽象，学生才会最深刻，也最容易透过现象看清本质。因此，我们把找这个中间量作为突破口，并且是用实验来突破了这个难点。

教学活动注重启发式教学，激发学生学习兴趣，引发学生积极思考，鼓励学生质疑问难，引导学生在真实情境中发现问题和提出问题。利用观察、猜测、实验、推理等方法分析问题和解决问题。通过实验，经历猜想—验证—得出结论的过程培养学生的推理意识。

【片段二】（实物演示，提出猜想）

师：孩子们请看，老师这里有一杯水，水平面刚好到达了这个排水口的位置。如果我把这个橘子轻轻放入水中，会怎么样？

生：水平面会上升。

师：那水会怎么样呀？

生：水会溢出来。

师：是吗？一起来看。果然如他所说，水怎么样啦？

生：溢出来了。

师：我们把溢出来的这些水，称为橘子放进水中排开的水，和老师一起读一遍—排开的水。

师：那这些排开的水的重量和刚才老师放进去的这个橘子的重量有什么关系呢？请你大胆猜一猜。

生1：我觉得它们的重量是相等的。

生2：我也觉得它们的重量是相等的。

师：还有同学想猜一下吗？

生：我觉得它们的重量是不相等的。

评析：这里利用实物实验，让学生观察到橘子放入装满的水杯里，水会溢出，这些溢出的水我们叫排开的水。接着引导学生自主提出猜想：排开的水的重量和放进去的橘子的重量有什么关系呢？巧妙引出突破本节课难点的关键“中间量”。

【片段三】（播放视频，验证猜想）

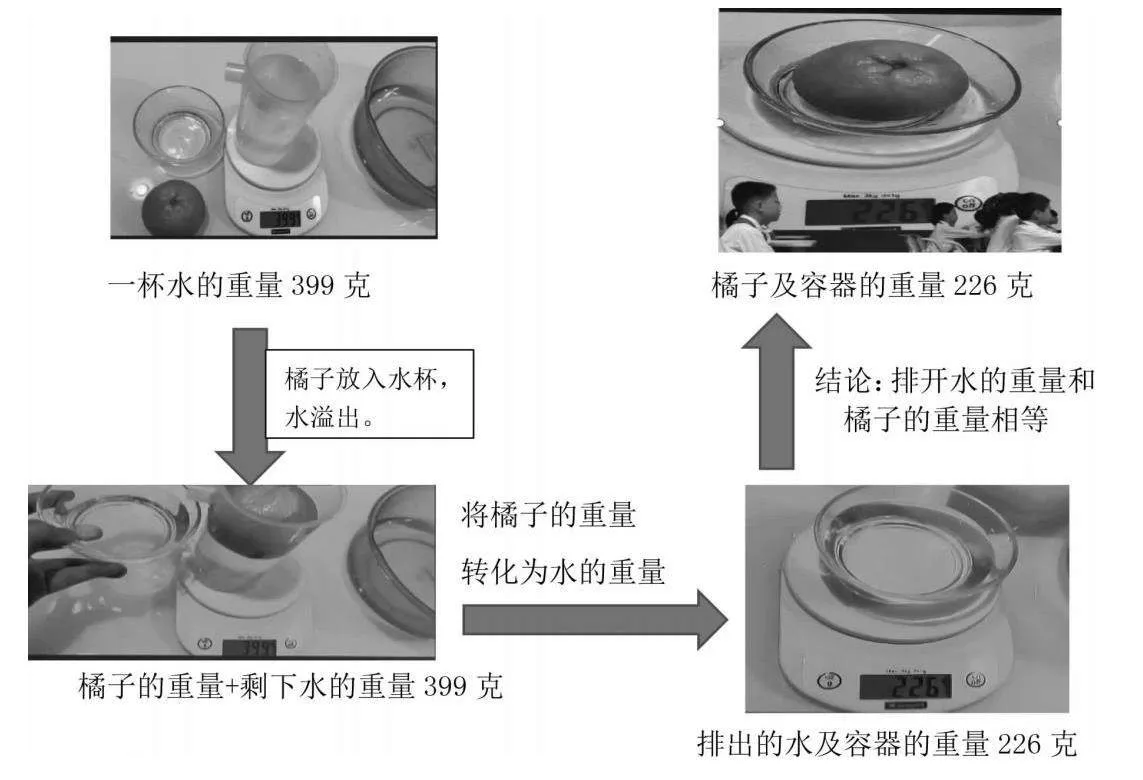
师：他们的猜想不一样，孩子们带着你们的猜想，接着往下看。桌面上这杯水显示399克。（如图1）

师：把橘子轻轻放入水中。看最终会显示多少克？

生：399克。（如图2）

师：把橘子和水拿开，再称一下排开水的重量是多少？

生：226克。（如图3）

师：再称一称橘子有多重？

生：226克。（如图4）

注：装水的容器和装橘子的容器重量相等。

师：你有什么发现？

生：我发现橘子的重量和排开水的重量一样多。

师：谁也想说一说你的发现？

生：我发现虽然它们差不多，可还是有一点点不同。

师：有不同吗？哪里不同？

生：我觉得有不同，因为橘子是有碗装着的。

师：水没有吗？

生：我觉得。橘子的重量和排开水的重量是一样的，因为水也有碗装着。

师：排开水的重量是多少？

生：排开水的重量也是226克，而橘子的重量也是226克，都用碗装着，所以我觉得它们的重量都相等。

师：说得真清楚。女孩你现在同意吗？都是多少克？

生：226克。

师：所以橘子的重量和排开水的重量怎么样？

生：相等。

师：所以橘子的重量和排开水的重量相等。和你们刚才的猜想一致的小朋友请举手。不过，同学们可不是所有的物体在水中都能得到这样的结论。咱们接着往下看。

师：如果我们放进去的物体进行替换，不再是橘子，换成苹果、梨、大象等会发生什么？

生：观看视频，得出结论：物体放到水中的重量=排开水的重量。

评析：本环节通过直观实验让学生感知一杯水的总重量是399克，将橘子放入杯子中后，有一部分水被排出到碗中，此时杯子剩下的水与橘子的总重量是399克。称量排开的水重量（包含容器的重量）为226克，称量橘子的重量（包含容器的重量）为226克，因此产生等式：排开水的重量+容器的重量=橘子的重量+容器的重量，由于容器的重量在等式两边都出现且相等，我们可以消去它，得到：排开水的重量=橘子的重量。但由直接代换容易让等量代换思维不足的学生无法理解抵消的过程，建议老师在上课的过程中测量容器的重量，通过计算的方法让学生直观地感受到代换的过程。例如，测量容器的重量为100克，那么排开水的重量为226-100=126克，橘子的重量=226-100=126克（也可以直接称量得到）。学生便可直观地得到橘子的重量=排开水的重量。我们再来看整个称量过程，一杯水、橘子的重量是没有变化的，把橘子放入水中后的总重量是：399+126，此时水溢出126克，如果把橘子拿走，把溢出的水倒入杯中，杯中的水恢复399克，这样的演示也能更好感受等量代换思想中总量守恒的思想。

最后进一步追问学生，如果我们放进去的物体进行替换，不再是橘子，换成苹果、梨、大象会发生什么？从而引导学生得到我们的第二个结论：物体放到水中的重量=排开水的重量。从“橘子”推广到“任何物体”为突破本节课难点打下坚实的理论基础。

这里我们需要注意一个问题，实际上阿基米德的浮力定律它是有一定的条件性的。物体浮在水上是一个结果，沉下去又是另一个结果。在上这节课的时候，要避免学生认定所有放到水里面排出来的水的重量都和我们物体的重量相等，所以在对三年级的孩子解释阿基米德的浮力定律时，我们就用了通俗易懂的语言，用了这样一个词“此时”，也就是说我们在做这个实验的时候，物体的重量是等于排开水的重量的。老师们在上课时应该要具有科学的严谨性。

活动三：合作探究，得出结论

回顾曹冲称象的过程，在这个过程中出现了大象的重量、排开水的重量、石头的重量。借助刚才的实验，和你的同伴说一说，这三个量之间有什么关系？记录在作业单上。

学生汇报，得出结论：

因为，大象的重量=排开水的重量；

又因为，排开水的重量=石头的重量；

所以，大象的重量=石头的重量。

小结：（1）在这个过程中，排开水的重量就是中间量。（2）因为两次称量到了同一刻度线，所以排开水的重量是相等的。大象的重量就等于石头的重量，等量的等量相等，这就是曹冲的智慧所在。

评析：回顾曹冲称象的过程，在这个过程中出现了大象的重量、排开水的重量、石头的重量。此环节引导学生结合实验的过程，学以致用到曹冲称象的故事里，并通过小组与师生之间充分的交流，促使学生在思考中自主归纳出：“大象的重量=排开水的重量”和“石头的重量=排开水的重量”，根据等式传递性推出“大象的重量=石头的重量”。在这样的过程中，排开水的重量就是中间量，因为两次称量到了同一刻度，所以排开水的重量是相等的，大象的重量就等于石头的重量，这就是等量的等量相等，也就是“曹冲称象”的智慧所在，也是本节课难点所在：理解“曹冲称象”中大象重量和石头重量相等的原理，找到中间量。体会等量的等量相等，培养学生的推理意识。

【注：本文系人民教育出版社课程教材研究所课题研究成果，课题名称：新课标背景下“教学评”一致性理念在小学数学中的实践研究；课题批准号：KC2023-024】