基于SARIMA-VMD-LSSVM的水产养殖溶解氧质量浓度预测

收稿日期：2023-05-25

基金项目：四川省科技成果转移转化示范项目（2020ZHCG0076）；工业控制技术国家重点实验室开放课题（ICT2022B45）

作者简介：唐 毅（1997-），男，四川江油人，硕士，主要研究方向为机器学习、智能水产养殖。（Tel）13320889755；（E-mail）tangyi970516@163.com

通讯作者：徐 全，（E-mail）quanxnjd@sina.com

摘要： 为了充分利用溶解氧质量浓度的数据特征，进一步提高水产养殖中溶解氧质量浓度预测的准确性，提出“线性与非线性”与“分解-预测-集成”相结合的溶解氧质量浓度预测模型。该模型首先由季节性差分自回归滑动平均（SARIMA）模型对溶解氧质量浓度随着时间变化而组成的数据序列（简称溶解氧质量浓度的时间序列）进行线性拟合，使用变分模态分解（VMD）对残差序列进行分解，然后将各残差分量代入经改进的灰狼算法（IGWO）优化的最小二乘支持向量机模型（LSSVM）中，得到非线性分量的预测结果。最后集成线性与非线性预测结果，得到最终的溶解氧质量浓度预测值。结果表明，与SARIMA、LSSVM、VMD-LSSVM模型相比，基于SARIMA-VMD-LSSVM模型对溶解氧质量浓度进行预测的精度显著提高，预测的均方根误差（RMSE）为0.078 7，平均相对误差（MAPE）为0.022 6，说明该组合模型可有效提取溶解氧质量浓度的时间序列的多尺度特征，从而更精准地进行溶解氧质量浓度的预测。

关键词： 水产养殖；溶解氧；变分模态分解；组合预测方法；改进的灰狼算法

中图分类号： TP391；S912 文献标识码： A 文章编号： 1000-4440（2024）08-1473-10

PredictiMNP/kEgoEFb0DjfORnWYag==on of dissolved oxygen mass concentration in aquaculture based on SARIMA-VMD-LSSVM

TANG Yi， XU Quan， DU Bin， WANG Lei， YUAN Ruihao， YUAN Yu

（School of Mechanical Engineering， Xihua University， Chengdu 610039， China）

Abstract： In order to make full use of the data characteristics of dissolved oxygen mass concentration and further improve the accuracy of dissolved oxygen mass concentration prediction in aquaculture， a dissolved oxygen mass concentration prediction model combining "linear and nonlinear" and "decomposition-prediction-integration" was proposed. Firstly， the seasonal auto regressive integrated moving average （SARIMA） model was used to linearly fit the dissolved oxygen mass concentration time series， and the residual sequence was decomposed using variational mode decomposition （VMD）. Then， each residual component was substituted into the least square support vector machine （LSSVM） model optimized by the improved gray wolf algorithm （IGWO） to obtain the prediction results of the nonlinear component. Finally， the linear and nonlinear prediction results were integrated to obtain the final dissolved oxygen mass concentration prediction value. Experimental results showed that compared with SARIMA， LSSVM， and VMD-LSSVM models， the prediction accuracy of SARIMA-VMD-LSSVM model was significantly improved. The root mean square error （RMSE） was 0.078 7， and the mean absolute percentage error （MAPE） was 0.022 6， indicating that the combined model could effectively extract the multi-scale features of the time series of dissolved oxygen mass concentration， and achieve more accurate prediction.

Key words： aquaculture；dissolved oxygen;variational mode decomposition;combinatorial forecasting methods;improved gray wolf algorithm

在水产养殖中，溶解氧含量是养殖户关心的重要参数之一，其含量过高或不足，都会严重影响水生生物的生长与健康，直接决定着养殖对象的产量和品质。目前，调节溶解氧含量常用的方法有实时或定时调节，然而由于数据传输及增氧机的启动与停止都存在滞后性，仅依据现有数据进行溶解氧含量的调节，不仅难以改善水质，还可能引起水质指标的波动，不利于水生生物的健康[1]。因此，溶解氧含量的预测，能够帮助养殖户及时调控水质、优化养殖管理，最大限度地发挥水生生物的生产潜力，提高生产效益。

目前，统计预测、机器学习预测及组合模型预测等方法是对溶解氧含量进行预测的主要方法。其中，差分自回归滑动平均（ARIMA）模型是统计预测中最常使用的模型，如Park等[2]使用ARIMA模型对洛东江口水质进行预测。随着机器学习技术的不断发展，其在数据预测领域的应用也越来越广泛，在对水质的预测中也取得了不错的效果，例如，张梦迪等[3]用反向传播（BP）神经网络模型实现了对多水质参数的预测；龚怀瑾等[4]使用变尺度混沌搜索优化的最小二乘支持向量机（LSSVM）模型，实现了对溶解氧含量的预测。然而，单一模型难以全面有效地表征溶解氧质量浓度随着时间变化而组成的数据序列（简称溶解氧质量浓度的时间序列）的特征。因此，针对溶解氧含量的非线性与非平稳特征，“分解-预测-集成”的组合预测模型被广泛应用于水质预测中。刘晨等[5]为了降低溶解氧质量浓度时间序列的复杂性，使用集合经验模态分解（EEMD），再结合SVM实现了最终的预测。白雯睿等[6]将变分模态分解方法（VMD）与CNN-LSTM模型相结合，提升了溶解氧含量的预测精度。然而，上述方法未考虑溶解氧含量的数据特征，且在模型的选择上未考虑预测的时效性。

为了弥补上述单一模型与组合模型在水质预测中的不足，本研究提出1种基于季节性差分自回归滑动平均（SARIMA）-VMD-LSSVM的短时溶解氧质量浓度组合预测模型。SARIMA模型能够识别具有周期性与非平稳时间序列的线性规律，且结构简单，使用少量数据便可进行预测。VMD分解算法可用于充分削弱序列的非线性特征，同时能起到降噪的作用。LSSVM模型的训练速度快，适用于非线性回归问题，且对少量数据建模具有一定的优势。因此，本研究拟通过将3种算法进行串联组合用于水产养殖中溶解氧质量浓度的预测，并引入改进的灰狼算法优化LSSVM模型，以期避免LSSVM参数选择的盲目性，进一步提升预测精度。

1 基本理论与模型的构建

1.1 SARIMA模型

SARIMA模型是由Jenkins与Box提出的一种时间序列预测模型，由自回归模型（AR）与移动平均模型（MA）逐步发展而来，这类模型融合了时间序列分析和回归分析的优点，并在此基础上进一步发展，适用于存在周期性与非平稳性的序列，其一般形式如下：

1.4.2 改进的灰狼优化算法 GWO作为一种元启发式优化算法，可以用来优化LSSVM的惩罚参数γ、σ。然而，GWO算法与大多数智能算法一样，存在后期收敛速度慢、易陷入局部最优解等问题。因此，本研究引入非线性收敛因子，并结合麻雀算法中的探索者以提升算法跳出局部最优的能力与收敛速度。

（1）非线性收敛因子。在GWO算法中，收敛因子a从2到0线性递减，无法对全局与局部搜索能力进行平衡。非线性收敛因子呈抛物线状递减，有利于提升全局搜索能力，在迭代后期快速递减，有利于提升局部搜索能力。

a=2-2sinttmaxsin1μ（18）

式中，μ为调节系数，μ=0.5。

（2）麻雀算法优化。本研究将麻雀算法中探索者的大范围搜索能力引入灰狼算法[10]，用于进一步提升GWO算法的搜索范围与收敛能力。具体步骤如下：

步骤1：根据比例系数（ζ），将狼群划分为探索者狼群与跟随者狼群。

ζ=PNN-PN（19）

式中，N为灰狼总数；PN表示位置较好的探索者灰狼数量。

步骤2：探索者灰狼位置更新。

X（t+1）=X（t）e-tζ·tmax（20）

式中，ζ为[0，1]范围内的随机值。

步骤3：其他灰狼仍按照原灰狼优化算法进行位置更新。

1.4.3 改进的灰狼算法（IGWO）优化LSSVM 采用IGWO优化LSSVM的惩罚参数（γ）和径向基宽度（σ），并以LSSVM最小均方差函数（MSE）作为目标函数，其表达式见公式（21）。

minf（γ，σ）=1m∑mi=1（xi-x^i）2（21）

式（21）中，xi表示真实值；x^i表示预测值。

使用IGWO优化LSSVM模型的具体步骤如下：

步骤1：初始化参数。生成20只灰狼，每只灰狼对应1组LSSVM的γ、σ，设置其取值范围为（0.01～1 000.00），设置最大迭代次数为100。

步骤2：寻找最佳猎物。从第1只灰狼开始，根据公式（21）计算适应度，并按照适应度高低划分灰狼等级，适应度较佳的前3匹狼分别表示为α狼、β狼、δ狼，剩下的狼则全为ω狼。

步骤3：位置更新。根据公式（20）对探索者灰狼进行位置更新，根据公式（17）对其他灰狼进行位置更新。

步骤4：判断是否达到最大迭代次数，若达到，则输出最优参数组合。

1.5 SARIMA-VMD-LSSVM模型的构建

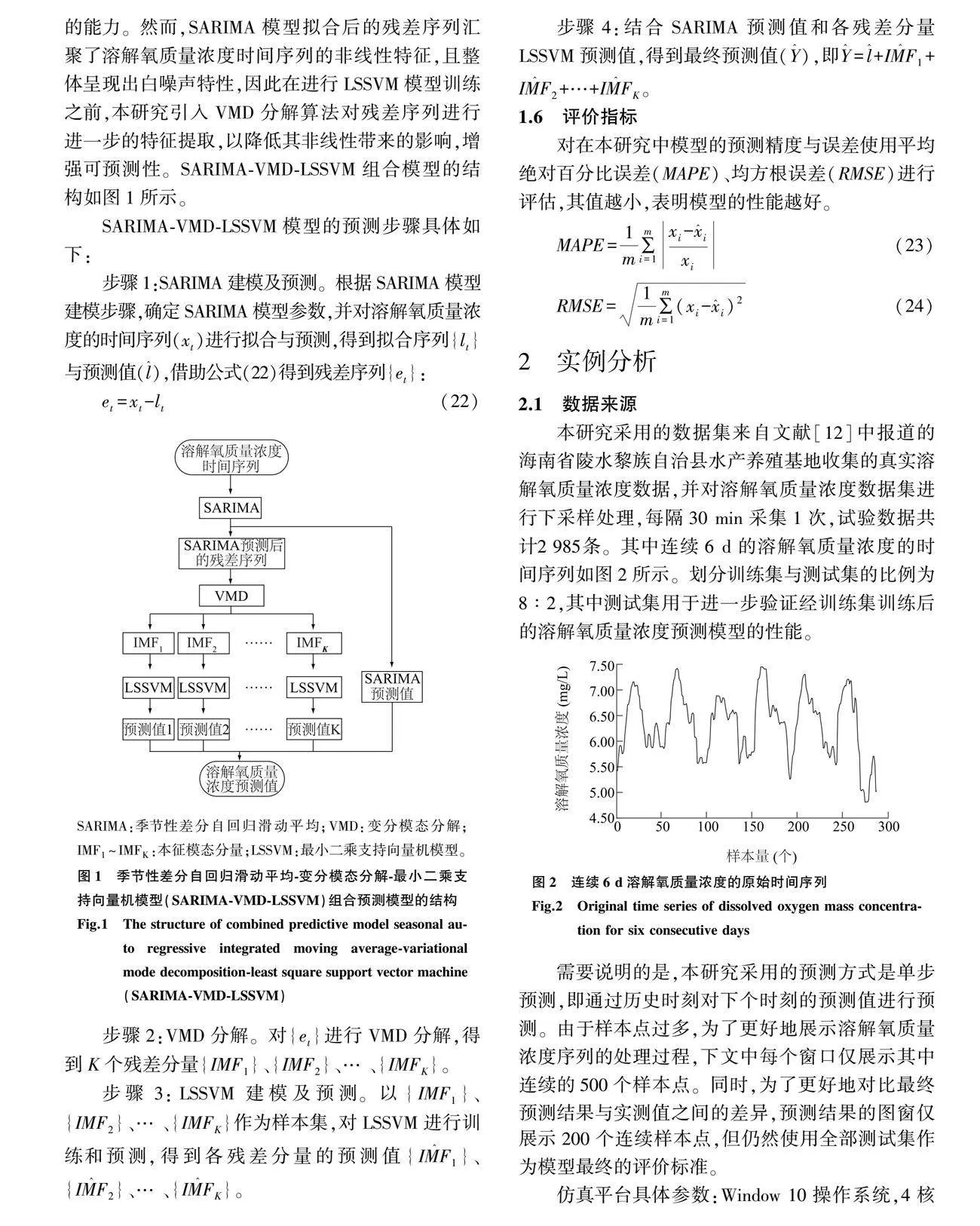
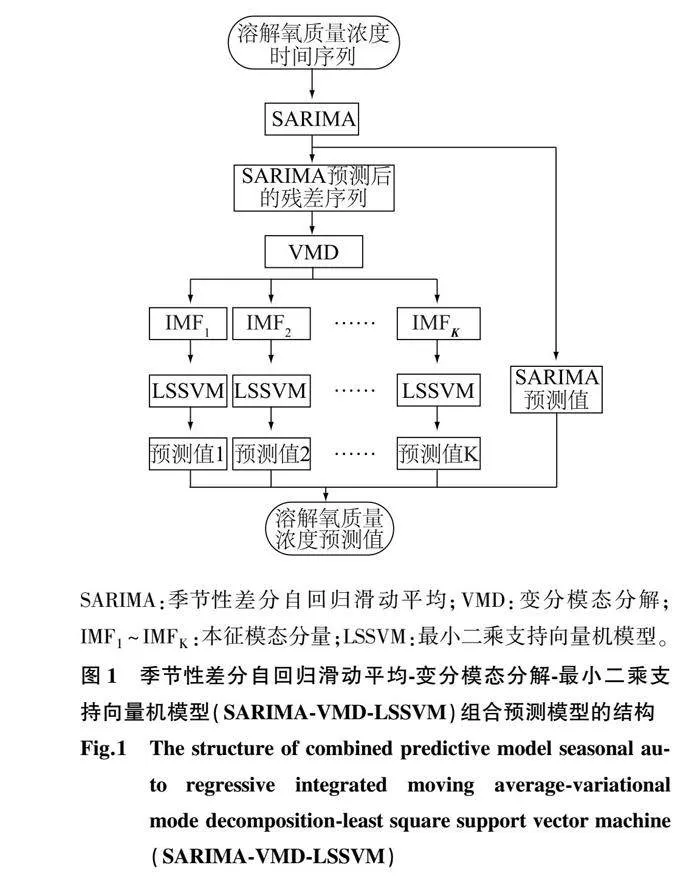
溶解氧质量浓度时序数据具有线性与非线性特征[11]，同时也存在周期性与非平稳性特征。由于单一模型无法适应所有特征结构的数据，因此拟合结果不佳。为了兼顾溶解氧质量浓度的所有数据特征，本研究提出基于SARIMA-VMD-LSSVM模型的水产养殖溶解氧质量浓度组合预测模型。其中，SARIMA模型能够较好地体现时间序列的线性与周期性特征，且结构简单；LSSVM模型训练速度快，适用于非线性回归问题。因此，本研究将SARIMA模型与LSSVM模型进行串联结合，以充分发挥各模型的能力。然而，SARIMA模型拟合后的残差序列汇聚了溶解氧质量浓度时间序列的非线性特征，且整体呈现出白噪声特性，因此在进行LSSVM模型训练之前，本研究引入VMD分解算法对残差序列进行进一步的特征提取，以降低其非线性带来的影响，增强可预测性。SARIMA-VMD-LSSVM组合模型的结构如图1所示。

SARIMA-VMD-LSSVM模型的预测步骤具体如下：

步骤1：SARIMA建模及预测。根据SARIMA模型建模步骤，确定SARIMA模型参数，并对溶解氧质量浓度的时间序列（xt）进行拟合与预测，得到拟合序列{lt}与预测值（l^），借助公式（22）得到残差序列{et}：

et=xt-lt（22）

步骤2：VMD分解。对{et}进行VMD分解，得到K个残差分量{IMF1}、{IMF2}、… 、{IMFK}。

步骤3：LSSVM建模及预测。以{IMF1}、{IMF2}、… 、{IMFK}作为样本集，对LSSVM进行训练和预测，得到各残差分量的预测值{IMF^1}、{IMF^2}、… 、{IMF^K}。

步骤4：结合SARIMA预测值和各残差分量LSSVM预测值，得到最终预测值（Y^），即Y^=l^+IMF^1+IMF^2+…+IMF^K。

1.6 评价指标

对在本研究中模型的预测精度与误差使用平均绝对百分比误差（MAPE）、均方根误差（RMSE）进行评估，其值越小，表明模型的性能越好。

MAPE=1m∑mi=1xi-x^ixi（23）

RMSE=1m∑mi=1（xi-x^i）2（24）

2 实例分析

2.1 数据来源

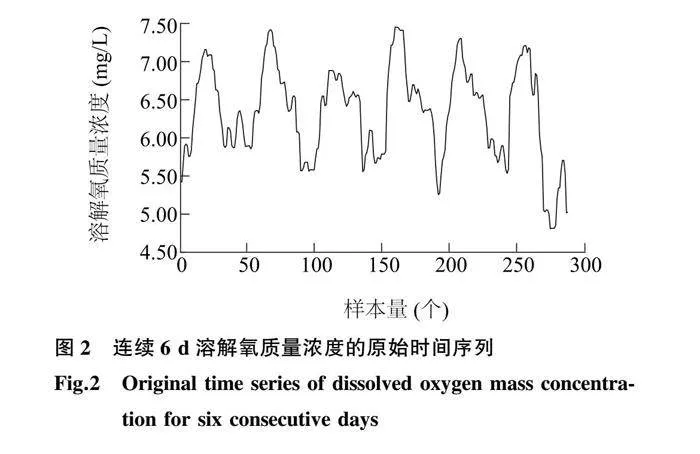
本研究采用的数据集来自文献[12]中报道的海南省陵水黎族自治县水产养殖基地收集的真实溶解氧质量浓度数据，并对溶解氧质量浓度数据集进行下采样处理，每隔30 min采集1次，试验数据共计2 985条。其中连续6 d的溶解氧质量浓度的时间序列如图2所示。划分训练集与测试集的比例为8∶2，其中测试集用于进一步验证经训练集训练后的溶解氧质量浓度预测模型的性能。

需要说明的是，本研究采用的预测方式是单步预测，即通过历史时刻对下个时刻的预测值进行预测。由于样本点过多，为了更好地展示溶解氧质量浓度序列的处理过程，下文中每个窗口仅展示其中连续的500个样本点。同时，为了更好地对比最终预测结果与实测值之间的差异，预测结果的图窗仅展示200个连续样本点，但仍然使用全部测试集作为模型最终的评价标准。

仿真平台具体参数：Window 10操作系统，4核1.80 GHz CPU，MatlabR 2022b。

2.2 SARIMA线性预测

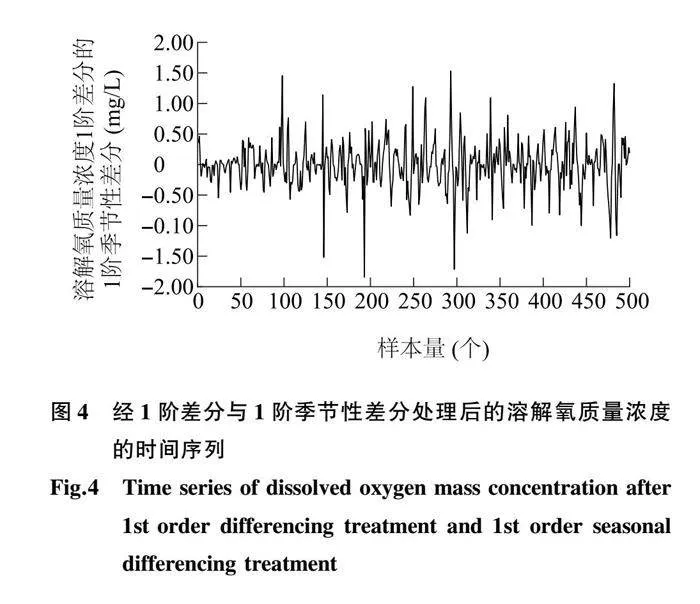
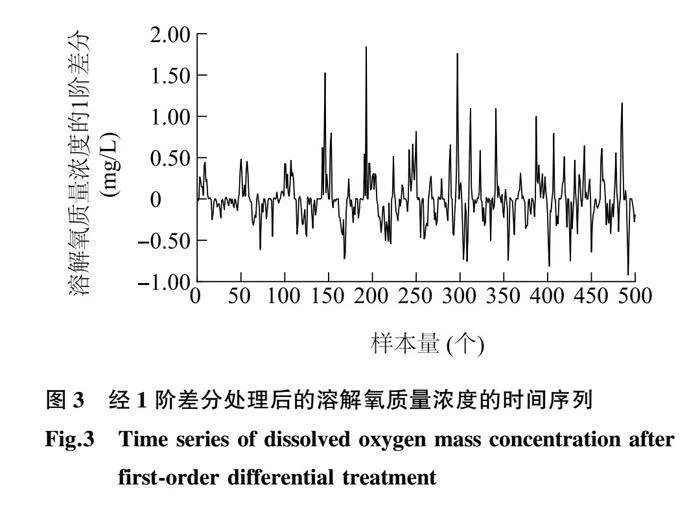
2.2.1 平稳化处理 首先通过MATLAB中的adftest函数对溶解氧质量浓度的时间序列进行单位根检测（ADF），此时P=0.054 0（P>0.05），可知此时原溶解氧质量浓度的时间序列为非平稳序列。对溶解氧质量浓度的时间序列进行1阶差分处理后，P=0.001 0（P<0.05），此时溶解氧质量浓度的时间序列整体表现平稳。如图3所示，1阶差分处理后的溶解氧质量浓度的时间序列仍存在周期性变化，因此还需对其进行1阶季节性差分处理，结果如图4所示。

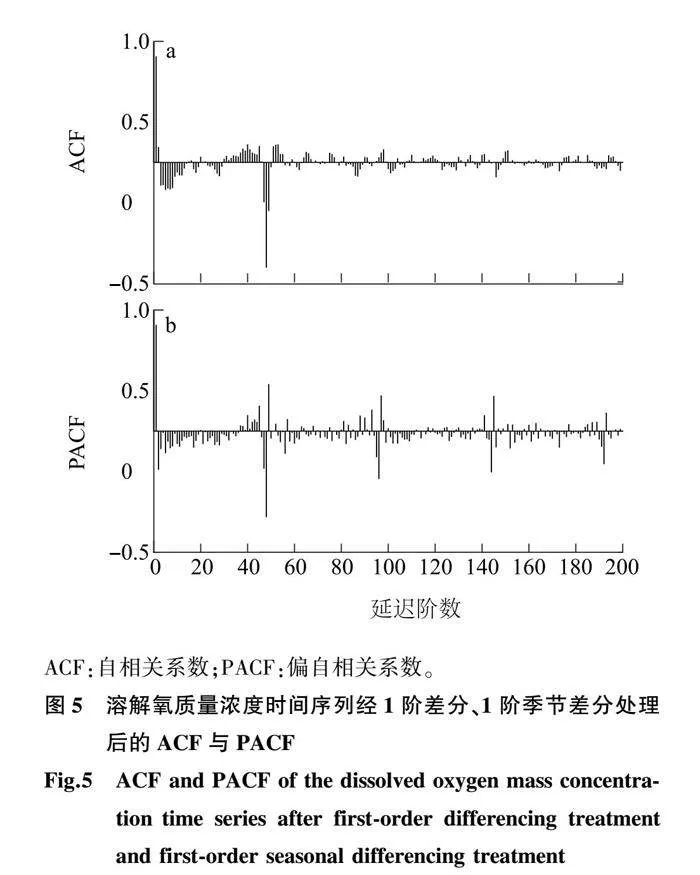
2.2.2 SARIMA模型参数定阶 对溶解氧质量浓度时间序列进行1阶差分与1阶季节性差分处理，则d=0或1，D=0或1。溶解氧质量浓度采样频率为1次间隔0.5 h，则s=48。由图5a可以看出，在延迟阶数为1阶、48阶时溶解氧质量浓度的时间序列数据与历史数据具有较强的相关性，即q=0或1，Q=0或1。由图5b可以看出，在延迟阶数为1阶、2阶时具有较强相关性，即p=0～2，在48阶、96阶、144阶时溶解氧质量浓度的时间序列数据与历史数据具有较强相关性，即P的取值范围为0～3。

根据参数p、d、q、P、D、Q的初步定阶结果，用SPSS中的正态贝叶斯信息量准则（BIC）确定最佳取值。正态BIC同时考虑模型拟合度与模型复杂度，其数值越小，表明模型越佳。最小正态BIC为-3.408，此时对应的最佳拟合度的模型为SARIMA（2，1，0）（1，1，1）48。

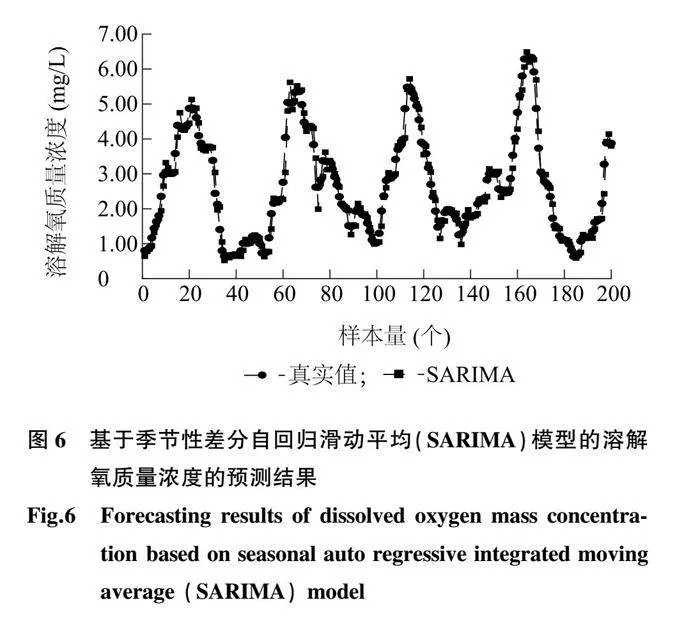
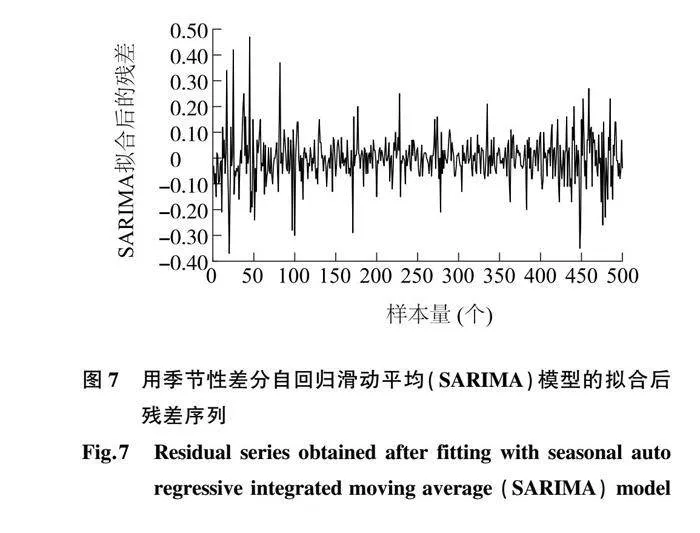
2.2.3 SARIMA对溶解氧质量浓度的预测 用SARIMA（2，1，0）（1，1，1）48对溶解氧质量浓度的时间序列进行预测，结果如图6所示。同时得到预测后剩余的残差序列，整体呈现白噪声特征（图7）。

2.3 VMD分解

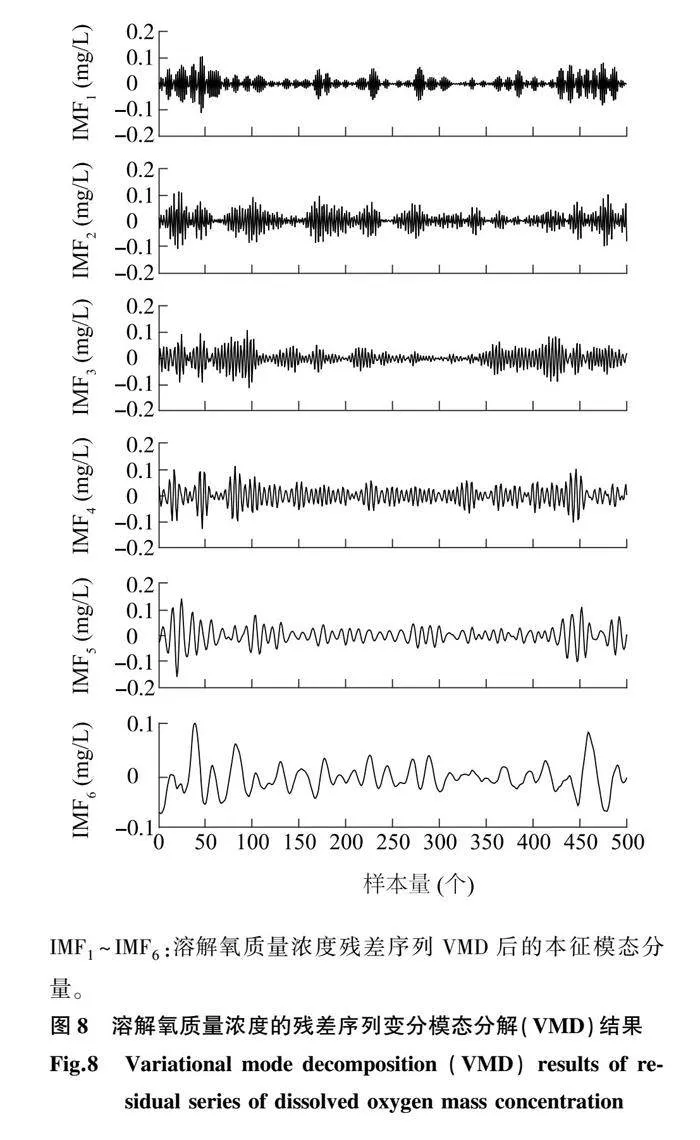
本研究依据最小峭度准则[13]，得到溶解氧质量浓度残差序列的最佳分解层数为6。由图8可以看出，各分量数据虽依旧保持较高频率，但VMD分解依旧能够分解出不同频率的信号，且更具有规律性，由此提升了残差数据的可预测性。

2.4 IGWO-LSSVM残差预测

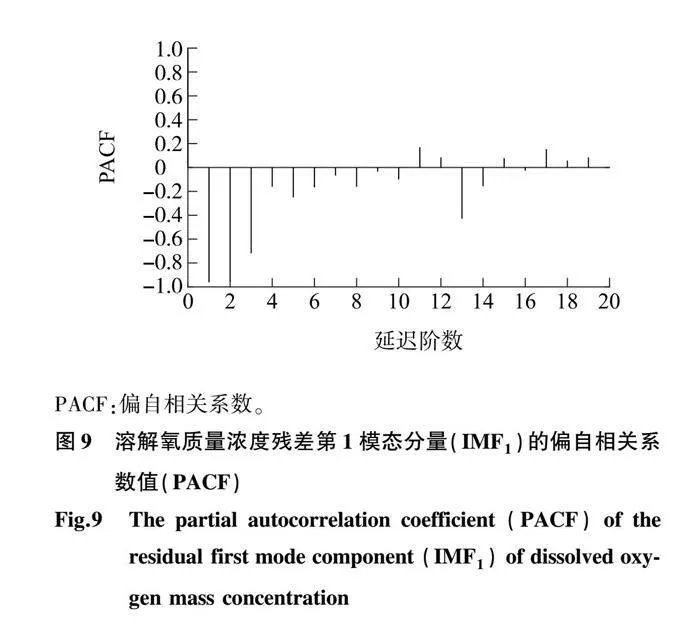
为了避免数据冗余带来的影响，本研究用偏自相关系数（PACF）确定各分量的最佳嵌入维数。如图9所示，前3个延迟（Lag）的偏自相关系数绝对值都大于0.6，说明IMF1时间序列在任意时刻的值都与其前3个历史时刻的值密切相关，因此取最佳嵌入维数（m）=3。同理，得到IMF2～IMF6的最佳嵌入维数，分别为4、4、4、4、3。

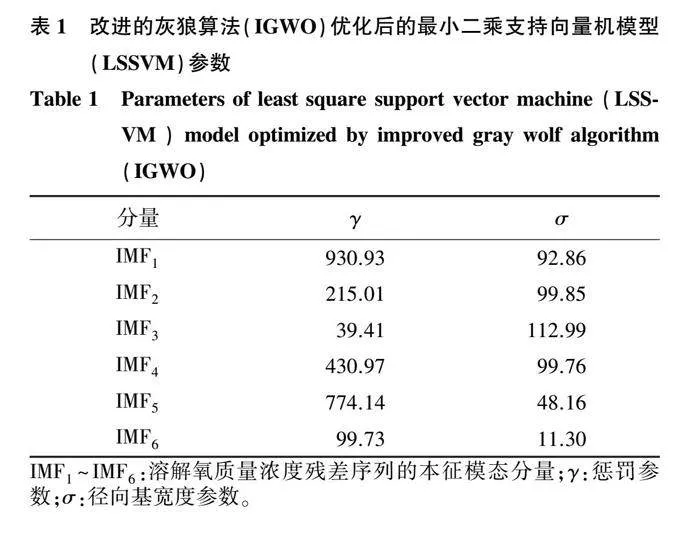
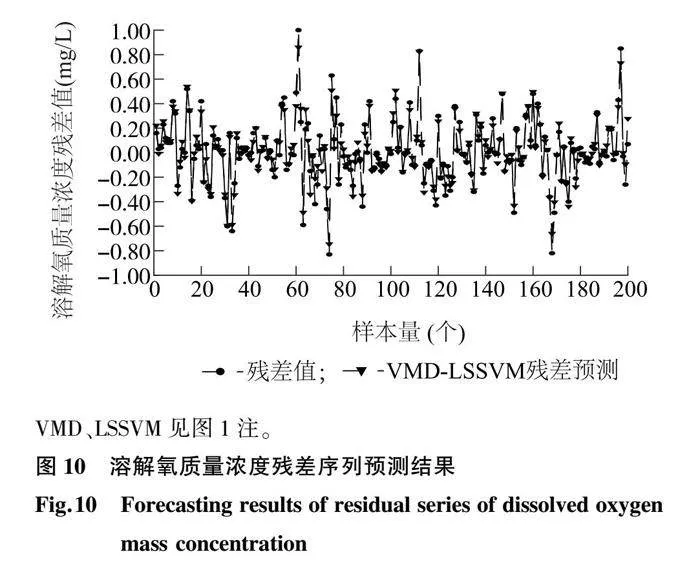
通过IGWO确定各残差分量的最佳LSSVM模型参数，详见表1。对各残差分量进行LSSVM建模预测，并将各分量的预测结果叠加，得到最终残差序列的预测结果，如图10所示。

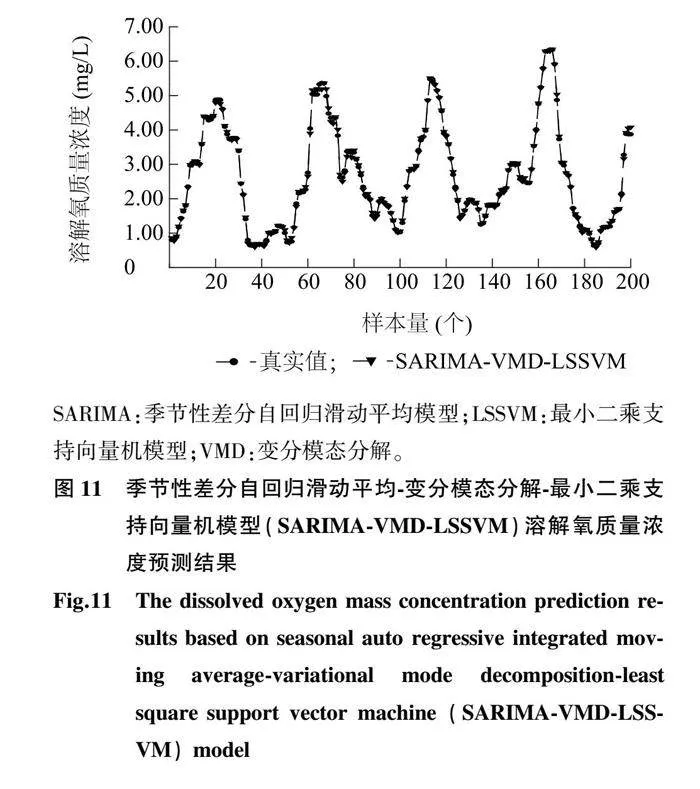
基于上述SARIMA模型，得到线性预测结果，其中通过LSSVM模型预测得到非线性结果，只需将2个分量进行集成，便可得到最终溶解氧质量浓度的预测值，结果见图11。

2.5 模型对比分析

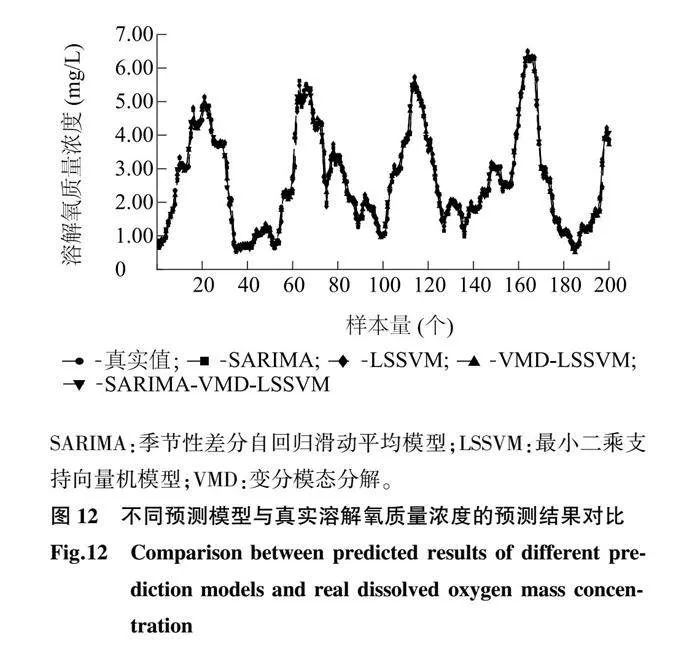
2.5.1 不同模型的对比分析 为了验证本研究所提模型的预测性能，将SARIMA-VMD-LSSVM模型与单一模型SARIMA、LSSVM及组合模型VMD-LSSVM进行对比分析。如图12所示，4种模型都能较好地预测溶解氧质量浓度的变化趋势，但是也能明显看出，SARIMA与LSSVM模型在转折点的精度较差，这是由于单一模型难以学习到转折点的信息。此外还可以看出，VMD-LSSVM与SARIMA-VMD-LSSVM的拟合程度较好。

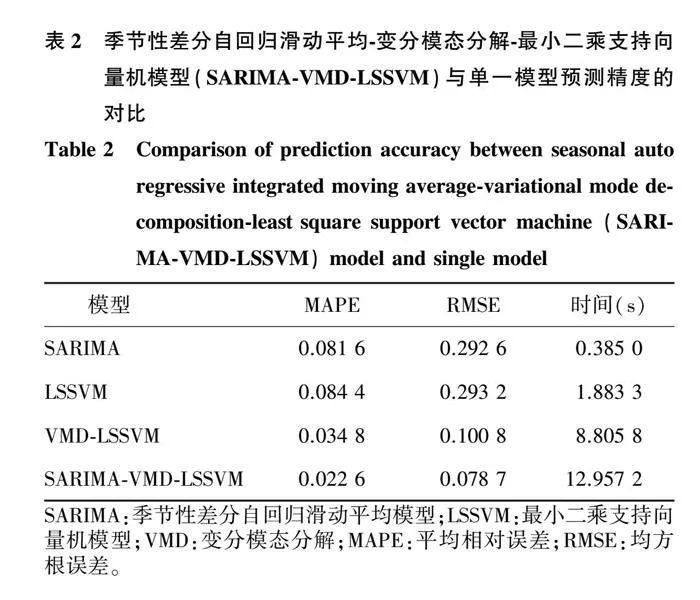
进一步计算出4种模型的平均相对误差（MAPE）、均方根误差（RMSE）并记录某一时刻所需的运行时间。如表2所示，与SARIMA、LSSVM模型相比，VMD-LSSVM、SARIMA-VMD-LSSVM组合模型的MAPE、RMSE明显降低，其中SARIMA-VMD-LSSVM模型相较于VMD-LSSVM模型有更好的预测精度，说明本研究提出的模型能更加充分地挖掘溶解氧质量浓度的数据特征。由表2还可以看出，SARIMA-VMD-LSSVM组合模型整体预测时间仅有12.957 2 s，可见该组合模型适用于溶解氧质量浓度的短时间预测。

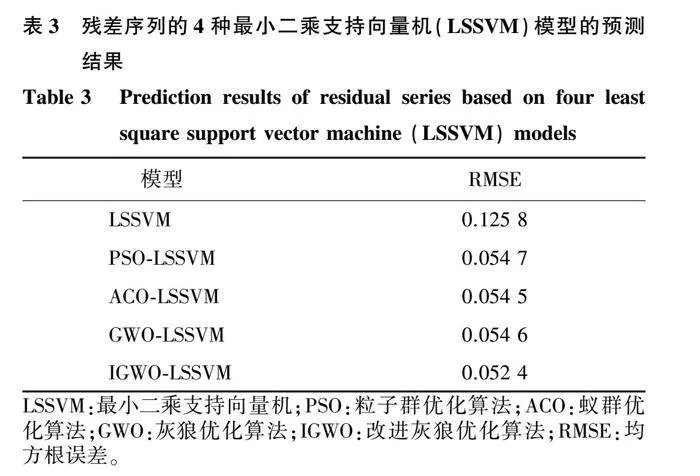
2.5.2 不同优化算法的对比 为了验证改进灰狼算法的有效性，本研究选用粒子群优化算法（PSO）、蚁群优化算法（ALO）、灰狼优化算法（GWO）、改进灰狼优化算法（IGWO）分别对LSSVM惩罚参数和径向基宽度参数进行寻优，并用优化后的LSSVM模型对SARIMA拟合后的溶解氧质量浓度残差序列进行预测。由于残差序列中存在值为0的情况，因此仅采用RMSE作为评价指标。在本研究中，设立种群数量为20个，最大迭代次数为100次。

对用4种优化方法预测溶解氧质量浓度残差序列的结果与真实残差值（表3）进行比较发现，使用固定超参数的LSSVM模型的RMSE明显较大，拟合程度不高，说明不同残差分量所需的LSSVM模型各不相同。加入优化算法后，RMSE减小，整体预测效果提升。由于LSSVM超参数较少，仅为二维，因此优化后的LSSVM模型预测效果相近，但仍然能看出IGWO-LSSVM模型的RMSE低于其他模型，其原因是对于其他模型而言，某些残差分量难以找到最优LSSVM模型，从而陷入局部最优。

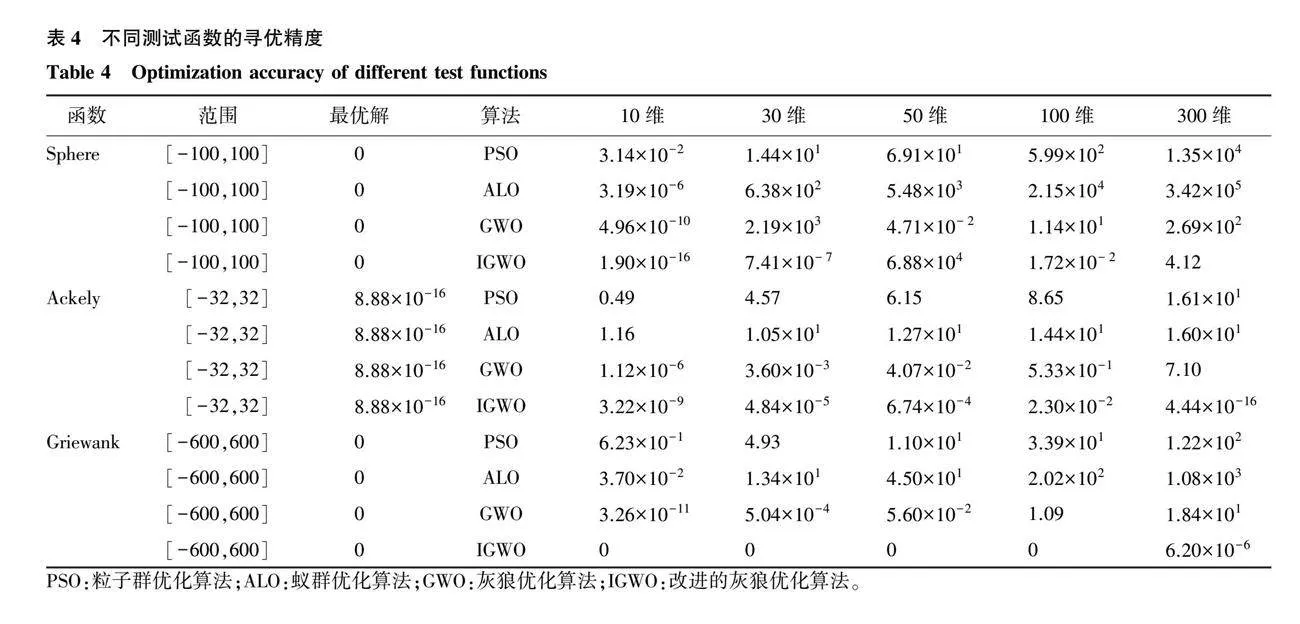
为了进一步验证IGWO的有效性，选取Sphere单峰函数、Ackely多峰函数和Griewank多峰函数进行测试[14]，并将测试结果与PSO、ALO、GWO算法所得结果进行比较，设各算法的种群规模为50个，最大迭代次数为100次。由表4可以看出，IGWO在不同测试函数中整体上有相对较好的寻优结果，其在不同维度下的Sphere函数的寻优精度较PSO、ALO和GWO算法高1～14个数量级。在不同维度下，Ackely函数IGWO算法的寻优精度比PSO、ALO和GWO算法高1～17个数量级。在Griewank函数中，IGWO算法在10～100维范围均获得理论最优值0；在300维，其理论最优值相较于PSO、ALO、GWO至少提升了7个数量级。由此可见，IGWO具有更好的全局搜索能力与收敛速度。

3 结论

为了充分利用溶解氧质量浓度的数据特征，进一步提升溶解氧质量浓度的预测精度，本研究将SARIMA模型、VMD模型与LSSVM模型相结合，同时引入改进的灰狼优化算法（IGWO），构建了用于预测水产养殖中溶解氧质量浓度的模型，得出以下结论：（1）通过改进GWO的收敛因子，并结合麻雀优化算法，有效提升了灰狼优化算法的寻优能力。避免了LSSVM参数设定的盲目性，减少了人工选择参数的主观影响。（2）将SARIMA模型、VMD模型与LSSVM模型3种模型结合，有效地表征了溶解氧质量浓度时间序列的周期性、线性、非线性与非平稳性特征。结果显示，SARIMA-VMD-LSSVM模型的评价指标优于其单一模型与VMD-LSSVM模型，表明该组合模型更能有效挖掘溶解氧质量浓度的数据特征。（3）本研究中组合模型的主要预测原理为SARIMA、LSSVM，两者都有较快的计算速度。试验结果表明，组合模型总用时为12.957 2 s，适合用于溶解氧质量浓度的短时预测。本研究主要针对溶解氧质量浓度单因子进行研究，未来将尝试将其与其他水质因子结合，以进一步提升预测精度。此外，还可以结合嵌入式、网络通信和自动控制等技术，实现溶解氧质量浓度的在线预测与管控。

参考文献：

[1] 谢雨茜， 李 路， 朱 明，等. 基于EMD与K-means的ILSTM模型在池塘溶解氧预测中的应用[J]. 华中农业大学学报（自然科学版），2022，41（3）：200-210.

[2] PARK K D， KANG D H， SO Y， et al. Water quality prediction using the ARIMA time series analysis model in the Nakdong River estuary[C]. San Francisco： AGU Fall Meeting Abstracts，2019.

[3] 张梦迪，徐 庆，刘振鸿，等. 基于动态滑动窗口BP神经网络的水质时间序列预测[J]. 环境工程技术学报，2022，12（3）：809-815.

[4] 龚怀瑾，毛 力，杨 弘. 基于变尺度混沌QPSO-LSSVM的水质溶氧预测建模[J]. 计算机与应用化学， 2013，30（3）：315-318.

[5] 刘 晨，李 莎，丛孙丽，等. 基于EEMD和萤火虫算法优化SVM的溶解氧预测[J]. 计算机仿真， 2021，38（1）：359-365.

[6] 白雯睿，杨毅强，郭 辉，等. 基于VMD-CNN-LSTM的珠江流域水质多步预测模型研究[J]. 四川轻化工大学学报（自然科学版），2022，35（4）：66-74.

[7] DRAGOMIRETSKIY K， ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing，2014，62（3）：531-544.

[8] LUO H， PAAL S G. Metaheuristic least squares support vector machine-based lateral strength modelling of reinforced concrete columns subjected to earthquake loads[J]. Structures，2021，33：748-758.

[9] MIRJALILI S， MIRJALILI S M， LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software，2014，69（3）：46-61.

[10]高 兵，郑 雅，秦 静， 等. 基于麻雀搜索算法和改进粒子群优化算法的网络入侵检测算法[J]. 计算机应用，2022，42（4）：1201-1206.

[11]胡衍坤，王 宁，刘 枢，等. 时间序列模型和LSTM模型在水质预测中的应用研究[J]. 小型微型计算机系统，2021，42（8）：1589-1573.

[12]LIU J T， YU C， HU Z H， et al. Accurate prediction scheme of water quality in smart mariculture with deep Bi-S-SRU learning network[J]. Ieee Access，2020，8（99）：24784-24798.

[13]郑 圆，胡建中，贾民平，等. 一种基于参数优化变分模态分解的滚动轴承故障特征提取方法[J]. 振动与冲击，2020，39（21）：195-202.

[14]崔东文，袁树堂. 基于WPD-AHA-ELM模型的水质时间序列多步预测[J]. 三峡大学学报（自然科学版），2023，45（1）：6-13.

（责任编辑：徐 艳）