基于二阶自抗扰的永磁同步电机矢量控制

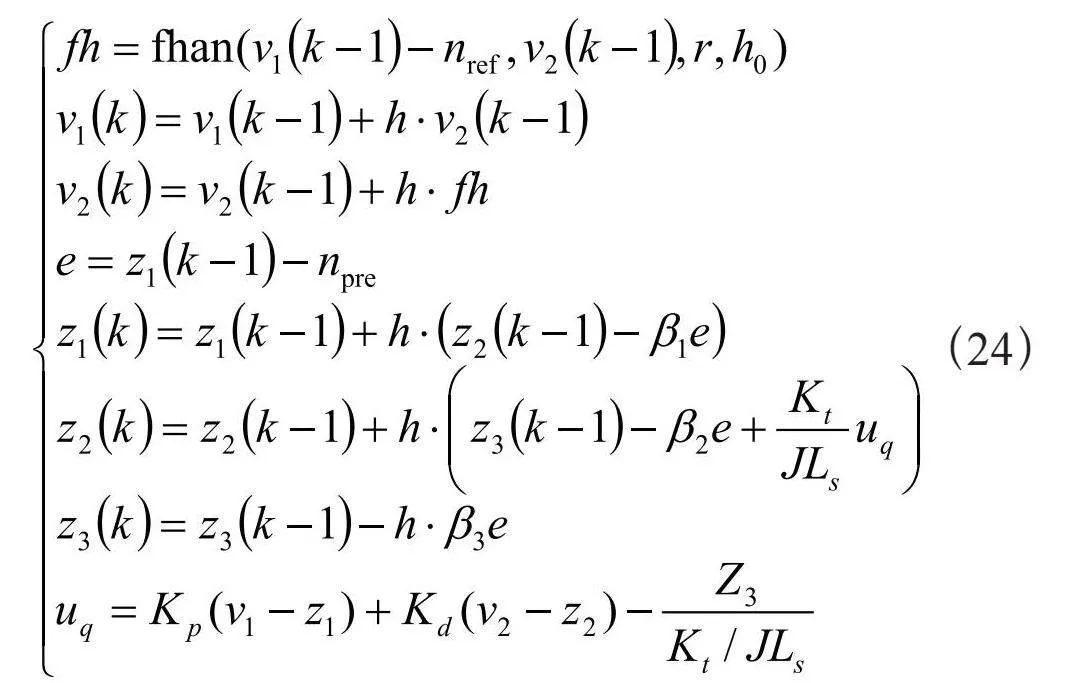
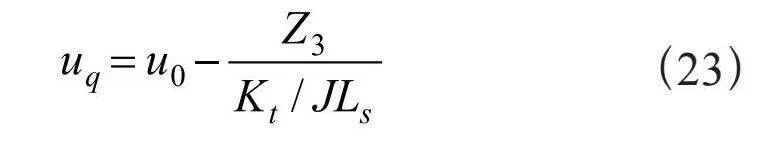
摘 要：针对永磁同步电机调速系统易受突变负载影响导致转速下降的问题，结合二阶自抗扰控制器，实现了电机自抗扰控制。首先，给出了电机d-q轴数学模型，解决了ABC坐标系下电机多变量、非线性等问题；其次，针对电机d-q轴下的数学模型研究了q轴二阶自抗扰控制器；最后，在MATLAB/Simulink中进行了变速和加负载仿真，结果表明，二阶自抗扰控制器具有较好的鲁棒性、抗扰性和动态响应性。

关键词：永磁同步电机；二阶自抗扰；矢量控制

中图分类号：TP312；TM341 文献标识码：A 文章编号：2096-4706（2024）13-0107-05

Vector Control of Permanent Magnet Synchronous Motor Based on

Second-order Active Disturbance Rejection

LIAO Xiaolu

（Unit 75842， Guangzhou 510599， China）

Abstract： In order to solve the problem that the speed of permanent magnet synchronous motor speed control system is reduced due to sudden load， a second-order active disturbance rejection controller is combined to realize the motor active disturbance rejection control. Firstly， the d-q axis mathematical model of the motor is given， and the problems of multi-variable and nonlinear of the motor in ABC coordinate system are solved. Secondly， the q-axis second-order active disturbance rejection controller is researched according to the mathematical model of d-q axis. Finally， variable speed and load simulation are carried out in MATLAB/Simulink. The results show that the second-order ADRC has good robustness， immunity and dynamic response performance.

Keywords： permanent magnet synchronous motor; second-order active disturbance rejection; vector control

0 引 言

永磁同步电机（Permanent Magnet Synchronous Motor， PMSM）凭借高功率密度、高效率等优势广泛应用于工业机器人、数控机床及航空航天设备等需要高性能的调速系统中[1]。目前，高性能系统对PMSM调速系统提出了更高的要求，系统在面临因突加负载等因素而导致转速突变时，不仅要减小转速的下降范围，还要保证系统能够在短时间内达到稳定状态[2-3]。

电机常用的转速和电流控制器有PI、滑模控制（Sliding Mode Control， SMC）和自抗扰控制（Active Disturbance Rejection Control， ADRC）三种[4]。其中PI控制器是工程上应用较多的控制器，它利用误差信号计算控制器的输出，并通过比例和积分两个参数来调节控制器的性能[5]。SMC是一种以系统非线性特性为前提，基于滑模曲线的概念使系统在滑模面上运行，从而实现对系统的控制[6]。然而，这两种控制器的鲁棒性受限，在面临电机突加负载情况时难以以较快的响应速度恢复到给定转速，加之SMC对系统模型的精确性要求较高[7-9]。因此，具有强鲁棒性和良好动态性能的ADRC控制器是目前电机驱动界的研究热点。李培康等设计了基于负载估计的复合自抗扰调速策略，将PMSM驱动系统负载突变时转速最大减少量抑制到30% [10]。李白雅等为了实现在系统具有良好鲁棒性的同时缩短系统的过渡时间，采用Sigmoid函数对自抗扰控制进行了改进，该方法比传统ADRC的抗扰能力更强，恢复时间更短[11]。

当前，大部分研究人员对电流环和转速环仅研究了ADRC，其形式均为一阶，而一阶形式中包含的过渡过程无法产生微分信号，后续的误差反馈过程只能成比例形式的体现；若将ADRC拓展为二阶形式则可产生微分信号。结合上述问题，本文的主要工作安排如下：

1）对PMSM电压和磁链方程进行坐标变换，给出电机d-q轴数学模型，解决了ABC坐标系下PMSM存在的多变量、非线性等问题。

2）在id = 0矢量控制策略框架下，将转速环控制器和q轴电流环控制器合二为一，研究了二阶形式的ADRC，该形式控制器在实现无超调的同时提高了系统的动态性能。

3）在MATLAB/Simulink仿真环境中搭建了PMSM矢量控制系统，证明了所提方法的有效性和优越性。

1 PMSM数学模型

PMSM在传统ABC坐标系下的电压和磁链方程表示如下：

式中，uA、uB、uC、iA、iB、iC、ψA、ψB、ψC分别表示ABC坐标系下的电压、电流和磁链值；ψf表示永磁体磁链值；Rs表示定子电阻值；θe表示转子电角度。在式（2）磁链方程中三相绕组自感的表达式如下：

结合式（1）（2）（3）可以看出，PMSM在传统ABC坐标系下电压和磁链方程具有多变量、强耦合及非线性的特点，需将其坐标变换到d-q坐标系下以减少变量和消除非线性，d-q坐标系下电压和磁链方程可表示为：

式中，ud、uq、id、iq、ψd、ψq分别表示同步旋转坐标系下的d轴和q轴电压、电流和磁链；ωe表示转子电角速度。

此外，在后续研究二阶ADRC时还需给出d和q轴下的运动方程和电流方程，其形式如下：

式中，ωm表示机械角速度，TL表示负载，B表示摩擦系数，Kt表示推力系数，对ωm再次求导，并将电流状态方程代入，进行一定的变换，得到如下方程：

2 二阶自抗扰控制器ADRC

二阶ADRC具体共分为三个环节，即过渡过程、扩张状态观测器及线性状态误差反馈，下面对这三个环节进行理论推导并给出最终的二阶ADRC形式。

2.1 过渡过程

传统PI控制器无法在保证速度的同时解决超调问题，而跟踪微分器（Tracking Differentiator， TD）可以解决这个矛盾，即能够以无超调形式使PMSM快速达到稳定状态，因此过渡过程采用跟踪微分器可显著提升二阶ADRC的转速跟踪效果。

跟踪微分器属于二阶微分环节，该环节能够将原信号和微分信号从PMSM系统中含有的噪声信号值中提取出来，从而消除了经典微分将噪声放大的弊端。另外，该形式的传递函数虽然能够较为准确地获得微分信号，但由于其惯性时间常数太小，最终会对所采集信号中包含的噪声信号产生放大效应，从而使得微分信号因被噪声覆盖而失真。

为解决微分信号被噪声信号覆盖的问题，跟踪微分器采用如下近似微分形式的传递函数：

式中，r表示转速因子，该值的大小可以改变二阶系统对原信号的跟踪效果，其值越大系统对原信号的跟踪越快，最终获得的微分信号也会更为精准。

在上述基础上，还可以进一步利用最速跟踪微分器来实现快速准确输入信号的跟踪效果，并获得较高质量的微分信号，最速跟踪微分器形式如下：

式中，v1受加速度 ≤r限制，将快速跟踪输入信号v0（t），r越大跟踪越快，状态变量v2为v1的微分信号，若r足够大，则可近似等于输入v0。将其利用欧拉法离散化：

式中，v表示输入信号，v1和v2分别是对输入信号的跟踪及其微分，h0表示滤波时间常数，一般取步长h的整数倍。

此外，式中新引入的函数fhan（v1，v2，r，h）形式如下：

输入信号取nref（为PMSM给定转速），则二阶ADRC过渡过程方程如下：

2.2 扩张状态观测器

扩张状态观测器（Extended State Observer， ESO）是整个二阶ADRC的核心，ESO用于对未知负载扰动进行估计，确定内部状态信息并让二阶ADRC做出抗扰调节实现自抗扰。ESO将影响系统输出的内部因素和外部因素作用的和视为总扰动项，并将其扩展成一个新的状态变量，使状态方程阶次比系统阶次高一阶，故被称为扩张状态观测器。

对于二阶系统，状态方程可表示为：

式中，f （x1，x2，t）表示内部扰动项，ω（t）表示外部扰动项，两者相加则表示系统总扰动，将其设为a（t） = f （x1，x2，t） + w（t），若再将该总扰动扩展成新的状态变量x3（t） = a（t），则原系统状态方程变为：

进而可得出如下形式的ESO：

由式（16）可知，在b已知的情况下，ESO能使z1和z2实现跟踪系统状态变量的目的。此外，z3用于对前述总扰动项进行估计。对式（16）进行离散化，得到离散域下的ESO：

式中，β1、β2、β3表示ESO的增益，h表示采样周期。设观测器的带宽β0，则β1、β2、β3和β0之间满足如下关系式：

结合上述分析，对于PMSM调速系统而言，其总扰动可以根据式（7）确定，则其总扰动a（t）可以表示如下：

对于PMSM系统的ESO离散化状态方程如下：

式中，n表示系统的反馈转速，z1表示对转速信号n进行降噪和跟踪，z2表示对转速微分信号的跟踪，z3表示估计前述系统总扰动项a（t）。

2.3 线性状态误差反馈

状态误差反馈分为线性状态误差反馈（Linear State Error Feedback， LSEF）和非线性状态误差反馈（Nonlinear State Error Feedback， NLSEF）两种，状态误差反馈通过小误差实现大增益或大误差实现小增益的方式进行工程实践模拟，这样提高了闭环系统的动态性能。NLSEF通常比LSEF推导更为复杂，因此本文拟采用LSEF进行状态误差反馈。

对于二阶系统，当采用LSEF实现线性二阶ADRC时，该LSEF环节采用比例微分控制器即可，其具体形式为：

式中，Kp = / b，Kd = 2ωc / b，e1、e2分别表示原信号的误差和微分与ESO跟踪的系统状态变量之间的偏差。因此将（20）和（21）的变量相结合，得到本控制系统的控制率：

2.4 二阶ADRC总体整合

在2.3小节中得出误差反馈控制率后，需要将估计的扰动在控制输入中进行补偿后才能输出给定的uq信号。对应的扰动补偿如下：

此时，整个二阶ADRC内部的各模块已经推导完毕，将过渡过程、扩张状态观测器以及线性状态误差反馈整合成二阶ADRC后的整体方程为：

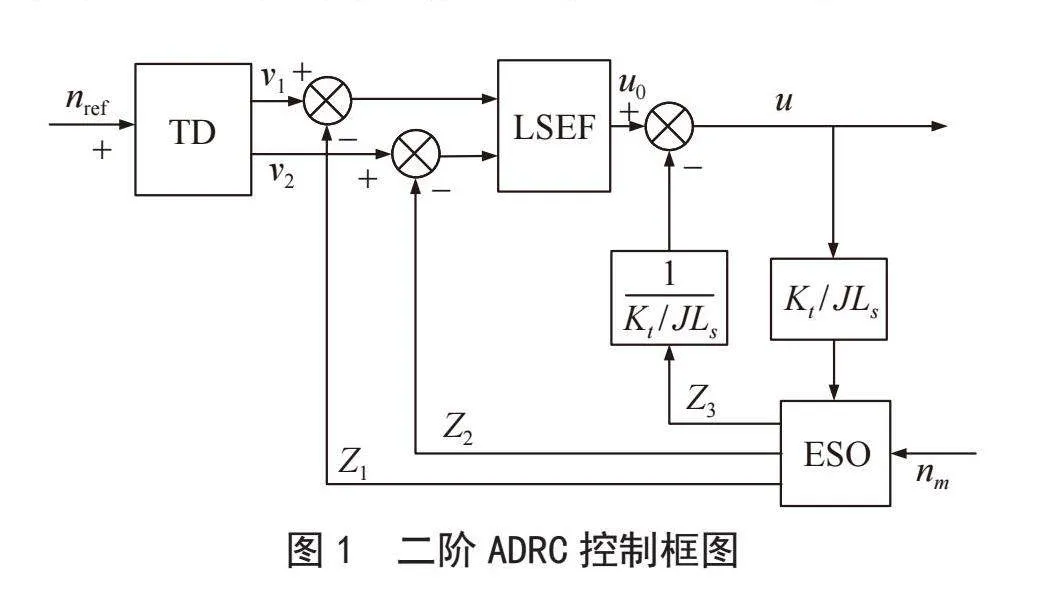
由式（24）得到二阶ADRC的控制框图，如图1所示，从控制框图中可以看出二阶ADRC利用ESO将反馈输入的机械转速进行扩展观测估计扰动，并与经过过渡过程后的给定转速作差，再由线性状态误差反馈给出电压指令控制后续脉冲波的调制。

3 仿真验证

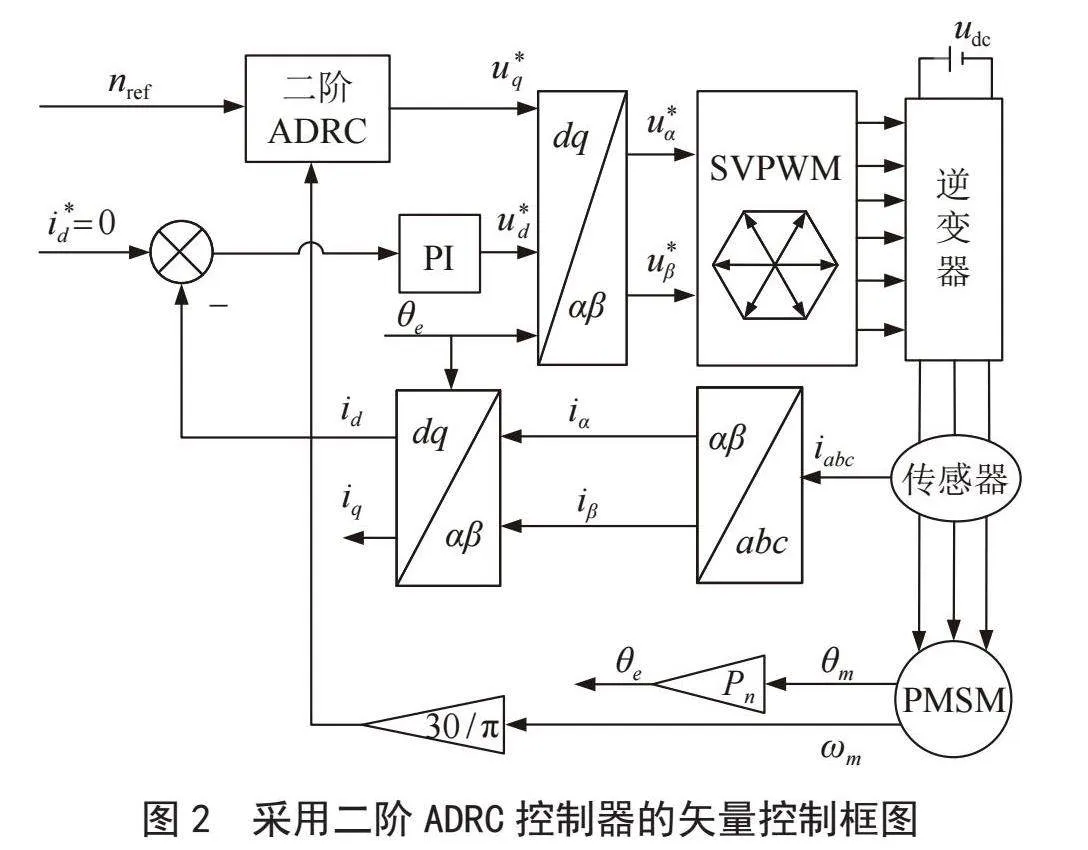
由以上推导得到采用二阶ADRC的PMSM矢量控制框图，如图2所示，将转速控制器和q轴电流控制器采用一个二阶ADRC代替，系统中q轴电流环开环处理。

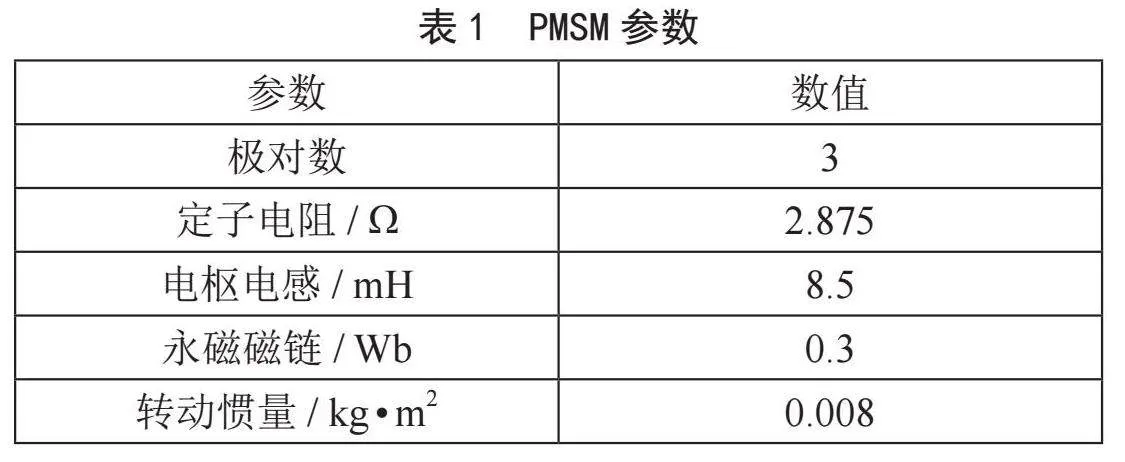
PMSM参数如表1所示。

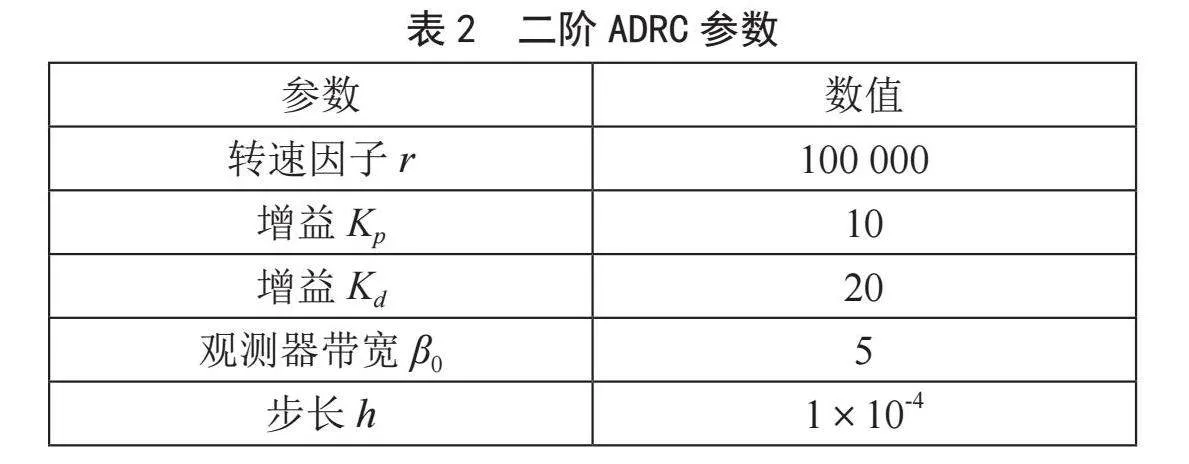
二阶ADRC各参数如表2所示，其中步长h也对应于系统仿真步长。

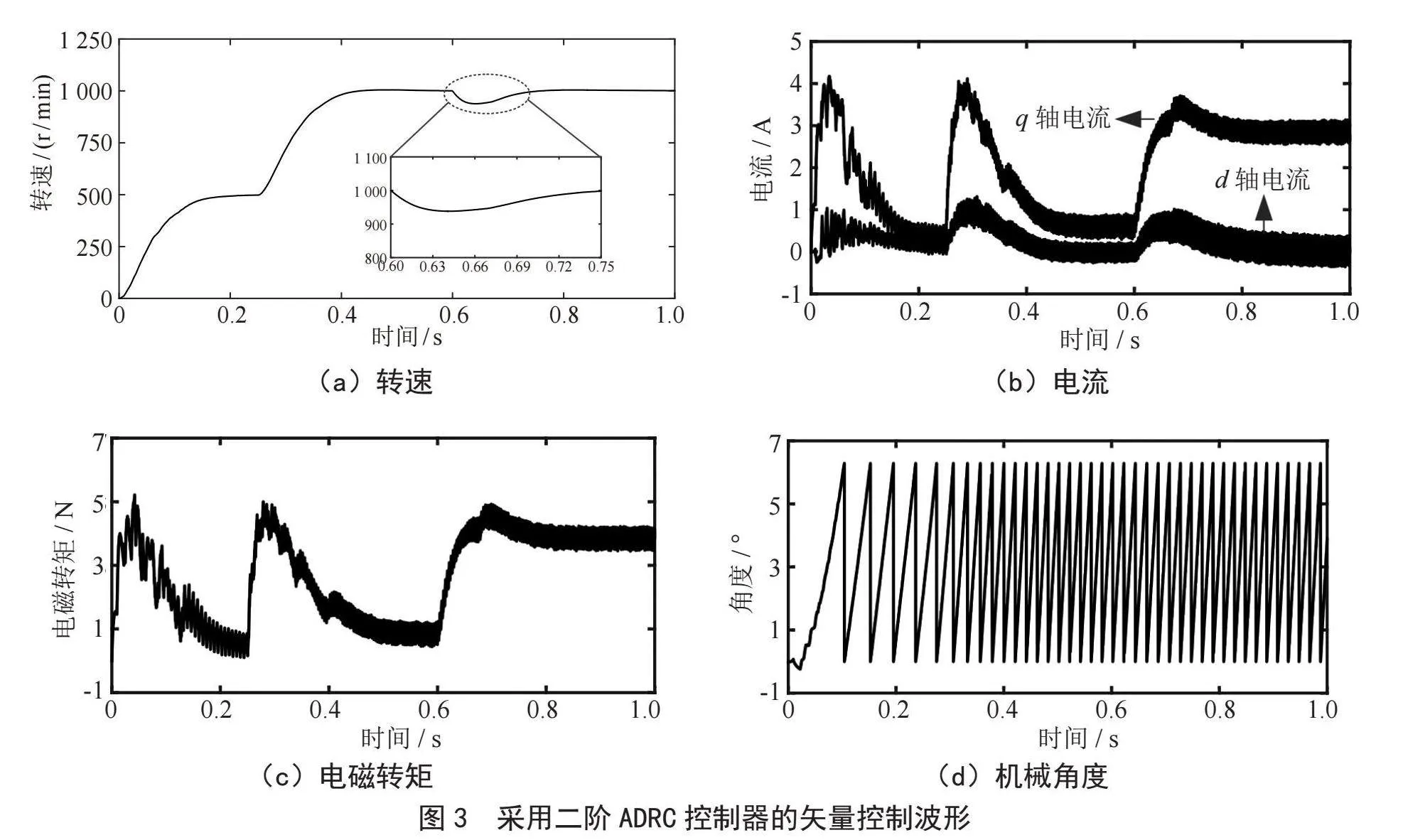
设定电机运行工况为变速、加负载，首先速度给定为500 r/min，待系统稳定后调速至1 000 r/min以验证中高速下电机调速性能，最后再突加3 N·m负载以验证ADRC的抗扰性能。

由图3中PMSM在变转速、加负载工况下的各种波形图可以看出，对于图3（a）的转速项，二阶ADRC在调速过程中的转速上升阶段，其均能以无超调的形式过渡到给定转速，其中，当突加负载时，由于二阶ADRC的自抗扰性能，转速在下降到最低点936 r/min时快速回升并达到给定转速1 000 r/min，转速下降率仅为6.4%。对于控制着电机转矩的q轴电流，如图3（b）所示，当突加负载后，电流迅速稳定到2.7 A，对于如图3（c）所示的电磁转矩，由于采用电机为表贴式PMSM，其电磁转矩大小仅由极对数、转子磁链及q轴电流决定，前两项对于特定电机均为常数项，因此电磁转矩与q轴电流的变化是同步进行的，二者大小仅相差特定系数，而图3（d）中的电角度则无太大变化，说明采用二阶ADRC能够实现较好的带载性能。

4 结 论

将PMSM矢量控制框架下的转速和q轴电流控制器合二为一研究了二阶ADRC控制器，该控制器能够对外加负载扰动实现快速响应，并能迅速调节转速在负载扰动时回到给定值。仿真结果表明，突加3 N·m负载时转速最大波动范围仅为6.4%，且能够调节电磁转矩平衡外加负载使系统以无超调形式迅速达到稳定状态。

参考文献：

[1] 罗润谦.新能源汽车用永磁同步电机的研究现状 [J].兵器材料科学与工程，2023，46（5）：154-158.

[2] 刘增文.永磁同步电机性能、控制和选用探讨 [J].中国设备工程，2023（11）：145-147.

[3] 丰飞.车用永磁同步电机控制系统安全稳定性研究 [D].上海：上海应用技术大学，2017.

[4] 张波.电动汽车用混合励磁同步电机关键技术的研究 [D].锦州：辽宁工业大学，2019.

[5] 王发良.永磁同步电机双闭环调速系统PI控制器设计 [J].南方农机，2022，53（3）：36-38.

[6] 程勇，李思卿，李森豪.永磁同步电机干扰观测复合滑模控制技术 [J].电机与控制应用，2023，50（3）：39-46+64.

[7] 杨义祥.基于改进型自抗扰技术的永磁同步电机系统研究 [D].北京：北京建筑大学，2022.

[8] 符梦虎，张倩，王群京，等.基于SVPWM的PMSM模糊PI-DTC控制研究 [J].传感器与微系统，2023，42（9）：68-71+76.

[9] 颜坤，马家庆.采样率对PMSM的SMC控制性能影响研究 [J].自动化仪表，2022，43（3）：34-37+45.

[10] 李培康，陆浩，李娟，等.基于负载估计的永磁同步电机复合自抗扰调速设计 [J/OL].南京信息工程大学学报：自然科学版[2023-12-02].https：//doi.org/10.13878/j.cnki.jnuist.20230919003.

[11] 李白雅，封志鹏，王锦涛，等.基于改进Sigmoid函数的PMSM调速系统自抗扰控制 [J].传感器与微系统，2023，42（6）：90-93.

作者简介：廖晓璐（1990—），女，汉族，湖北钟祥人，工程师，硕士研究生，研究方向：自动化、计算机。