变中有不变 思行出真知

善于发现和提出数学问题，对初中数学的学习非常重要。好的数学问题，往往能引领我们的数学学习走向深入。

折纸与剪拼

如果给你一张长方形纸片，你能提出什么数学问题呢？

相信你会有很多想法，比如，通过裁剪，能剪出什么样的几何图形？如何剪出正方形、平行四边形等特殊四边形？如何把长方形分成两个面积相等的图形？等等。最好的解决方法就是在尝试中发现，在实践中思考。快找一些长方形纸片试一试吧！

根据小学的学习经验，我们知道，如教材第8页图1-2进行裁剪，可以得到正方形。你能说说剪出图形是正方形的理由吗？是不是不同的长方形，通过这样的裁剪，都可以得到正方形呢？经过尝试，我们发现，尽管长方形在变，裁剪的结果却不变，依然是正方形。今后的数学学习，会帮你揭开其中的数学奥秘。

寻找不同图形之间的联系，可以提出有价值的数学问题。比如，三角形和四边形、五边形……n边形（n≥4）之间分别有什么联系？

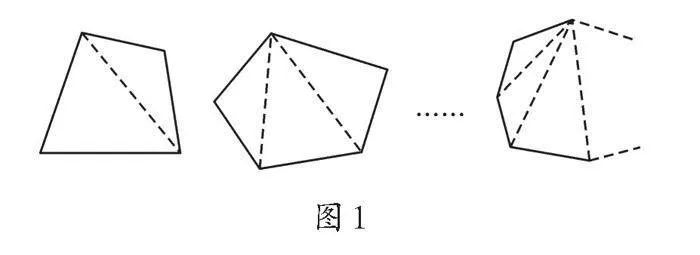
通过思考，我们发现，四边形、五边形……n边形（n≥4）都可以划分成若干个三角形（如图1）。那么，多边形的问题就可以转化为我们熟悉的三角形问题，从而利用三角形中不变的性质来解决。从陌生到熟悉，从变化到不变，转化的力量让我们在变化的数学世界中，发现不变的客观性质，感悟数学魅力。

月历中的数量关系

月历是生活中常见的物品，从中可以提出很多有价值的数学问题，丰富我们的数学思考。

月历中的日期排列有什么规律呢？这就是一个有价值的数学问题。我们可以先从简单规律开始探究，比如月历中方框内的4个数之间有什么样的数量关系（如教材第9页图1-4）？具体来说，左右、上下、对角两个数之间有什么数量关系？4个数的和与其中1个数有什么联系？方框移动后，以上规律仍然成立吗……

观察一个方框内的4个数，得出的规律还不一定正确，还需要多框几次，多次验证；还可以用字母表示数字，如设其中1个日期为x，用x表示出其他日期，得到更加“靠谱”的规律。 因此，我们在解决问题的过程中，可以通过尝试、猜想，发现结论，培养良好的数学直觉；也可以通过严密的思考推理求解，让我们的思维变得更加严谨。

研究完4个数的规律，接下来就可以探究更加复杂的规律啦！如9个数、16个数……

我们还可以提出更加生活化的数学问题。如小明一家暑假外出旅游5天，这5天的日期之和是30，那么小明一家是几号出发的呢？

仔细思考以后你会发现，这个问题的解法非常多。可以通过估算、验证的方法发现，连续5个数的和为30，那么第一个数不会超过6，再经过尝试，就可以得到第一个数是4；也可以设第一个数为x，可以得到这5个数的和为5x+10；还可以从特殊值——第3个数进行分析，发现中间数为6，继而得到第一个数是4。一个问题可以有这么多解法，是不是让你觉得很惊呀呢？有价值的数学问题，往往解法多样，就像一颗颗种子，只要你愿意思考，就能不断绽放思维的花朵，长出思维的果实。

通过上述探究，我们发现，尽管每个月的月历都有变化，但是月历中的规律是不变的。在变化的世界中，用数学的语言表达出不变的规律，是一件很酷的事呢！听说某同学研究出月历的规律后，用一张纸自制了月历尺，从此只要动动数框，就可以得到每个月的月历啦！感兴趣的你快去试一试吧！

1．对于长方形纸片，你还能提出哪些数学问题呢？

2．将长方形纸片裁剪成正方形，你还有其他裁剪方式吗？

3．自制一把月历尺，向同学们展示和交流。

（作者单位：南京师范大学附属中学新城初级中学黄山路分校）