关于“直线的倾斜角与斜率”的教学探究思考

[摘 要] “直线的倾斜角与斜率”是解析几何的重要章节，也是研究直线的知识基础. 在实际教学中，教师要深入解读知识内容，围绕知识重点来探究教学策略，分环节设计探究过程，合理设问引导学生逐步探究. 研究者深入解读章节知识，探索教学过程，并提出相应教学建议.

[关键词] 直线;倾斜角;斜率;探究教学

教学解读

“直线的倾斜角与斜率”是人教A版（2019）选择性必修第一册教材中的第二章“直线和圆的方程”的第二节内容，探究核心是直线的倾斜角和斜率的概念，以及直线的斜率公式. “直线的倾斜角与斜率”的前一章内容，主要是利用空间向量来研究立体几何，如位置关系、数量关系等. 可以说，这两章的研究核心是几何图形的探究方法.

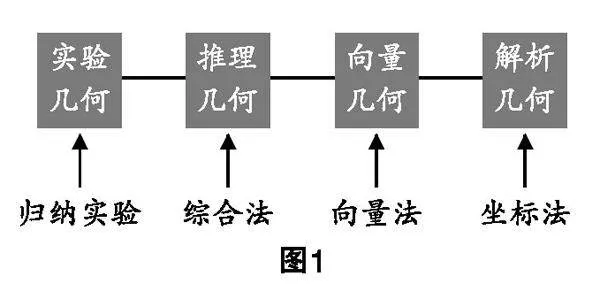
关于几何图形的探究方法（如图1所示），小学归纳实验，初中过渡到综合法，包括直观感知、操作确认、思辨论证、度量计算等，而高中则涉及向量法和坐标法，即利用向量法探究向量几何，利用坐标法探究解析几何. 在教学中，教师可以介绍解析几何的发展背景和思想方法，简单讲解本章节的研究重点，引导学生整体把握单元知识框架.

综上分析，本节课的教学目标主要有三个：一是让学生了解解析几何发展史、坐标法思想，掌握整个章节的探究方法;二是让学生理解倾斜角、斜率的概念，并掌握斜率公式;三是让学生掌握直线斜率与方向向量之间的内在联系.

教学过程

在教学中，教师采用“设问引导，过程探究”的方式，让学生充分参与课堂讨论，体验探究过程，体会知识生成. 教师要合理设计教学环节，随时关注学生的思维变化，适时设问引导，确保教学顺利推进. 本节课的内容承接前面的知识，学生虽具有一定的知识基础，但不熟悉如何利用坐标法来刻画直线的几何要素，因此教师要渗透坐标法思想，引导学生探究如何用坐标系来表示倾斜角. 虽然过程较简洁，但对学生的抽象思维的要求较高. 教师应在倾斜角概念的基础上归纳确定直线的方式，并以坐标法思想来启发引导学生学习. 后续分别从几何和代数两大角度进一步探究直线的斜率，并构建两者的联系.

作为高中解析几何板块的起始课，探究的首要内容是直线的几何要素，对其刻画445425c868e9019a9d7f620a4a8438d35540fea0cbb65e393f4343385638ea4b需要按照“方向→倾斜角→倾斜角的正切值→斜率”的思路来完成，逐步实现化“形”为“数”，利用“代数”相关知识来表示几何图形的内在联系.

上述解读了“直线的倾斜角与斜率”的核心知识内容和教学方法，下面具体讲解教学环节.

1. 情境引入

教师采用情境教学的方式，以生活中的实例作为问题背景，如给出图2（工程上常用“坡度”来描述一段道路相对于水平方向的倾斜程度），引导学生思考如何在平面内确定一条直线.

设计意图 引导学生回顾已学的知识内容，整体把握本节课的探究内容和重点，深化学生对解析几何思想和直线几何要素的理解，便于学生构建和完善单元知识体系，抓住知识间的内在联系.

2. 设问引导，过程探究

本节课的探究内容共三大项：一是直线的倾斜角;二是直线的斜率;三是方向向量与斜率的联系. 教师采用“设问引导，过程探究”的方式，引导学生参与课堂教学，完成知识的探究学习.

探究1 直线的倾斜角.

教师引导学生回顾前面学习的知识，思考如何确定一条直线，引导学生指出“点”和“方向”是确定直线的两个核心要素. 教师进一步提出如何将“方向”代数化，设置如下两个探究问题.

问题1：在平面直角坐标系中，过定点P作任意一条直线，观察对比所作出的直线有何差异.

问题2：将直线围绕点P进行旋转，观察变化过程，思考如何来描述直线的倾斜程度.

设计意图 利用问题1引导学生感受过点P的直线的不同，初步了解坐标系在方向刻画中的作用，为后续的定义探索做铺垫;借助问题2引导学生自主归纳，抽象倾斜角的概念.

给出倾斜角的概念后，继续引导学生思考两点，一是倾斜角的概念是否适用于所有直线，二是倾斜角的具体范围是什么. 通过上述思考来培养学生思维的严谨性，并构建如图3所示的知识导图，引导学生掌握重点知识：一是两点可以确定一条直线;二是从几何视角来看，“点”和“方向”是研究直线的两个几何要素，可利用倾斜角来刻画直线的方向.

探究2 直线的斜率.

通过知识内容的解读可知，在坐标法思想中，需要对倾斜角代数化，引出两点坐标与倾斜角的联系——直线的斜率. 教学中可以呈现如下三个探究问题，引导学生思考.

建立平面直角坐标系，设直线l的倾斜角为α.

问题1：已知直线l过点O（0，0），P（，1），则α与点O，P的坐标有何关系？

问题2：若直线l过点P（-1，1），P（，0），则α与点P，P的坐标有何关系？

问题3：若直线l过点P（x，y），P（x，y），则α与点P，P的坐标有何关系？

设计意图 设计上述三个问题，从特殊到一般逐步引入斜率的概念. 问题1由学生自主思考，旨在引导学生回顾正切函数的概念;问题2由学生互动交流讨论，旨在引导学生使用不同方法去解决，并启发学生结合平移思想，把向量法加入知识体系中;在此基础上，引导学生主动思考问题3，通过小组合作，构建倾斜角的正切值与两点坐标的联系（具体如下）.

直线l的倾斜角与直线l上的两点P（x，y），P（x，y）（x≠x）的坐标有如下联系：tanα=①. 我们把一条直线的倾斜角α的正切值叫做这条直线的斜率，常用小写字母k来表示，即k=tanα②.

完成上述定义的归纳总结后，进一步引导学生思考如下问题，让学生体会倾斜角与斜率的对应关系，理解斜率可以用来刻画倾斜角的合理性，增强思维的严谨性.

问题1：倾斜角与斜率是否为一一对应的关系？

问题2：当直线l的倾斜角由0°增大到180°时，斜率如何变化？

同时，结合生活中的坡度，构建如图4所示的知识导图，即数、形视角下的倾斜角与斜率的对照关系，以及两者关于“直线的方向”的刻画联系.

探究3 方向向量与斜率的联系.

教学预设：已知直线l经过两点P（x，y），P（x，y），且直线斜率为k，试用k表示直线的一个方向向量.

设计意图 设计思考环节，引导学生探究斜率与方向向量之间的关系，自主思考、总结归纳知识间的内在联系. 教师可以通过引导，为学生提供探究方向. 具体可以构建如下知识内容.

（1）若直线的斜率为k，则直线的一个方向向量为（1，k）;

（2）若直线的方向向量为（x，y）（x≠0），则斜率k=.

教学建议

1. 整合知识重点，教学核心突出

高中数学知识内容较多，章节教学时需要教师充分备课，整合知识重点，突出课堂教学重点. 以上述“直线的倾斜角与斜率”为例，围绕考试大纲，明确教学探究重点：一是直线的倾斜角;二是直线的斜率;三是方向向量与斜率的联系. 同时分析教学策略，采用“过程构建，引导探究”的教学方式. 上述策略，同样适用于解析几何相关知识的教学，如后续教学直线的方程、直线与圆的位置关系等，可以适度参考借鉴.

2. 设置知识导图，完善知识体系

知识导图是课堂知识整合、总结的重要方式，教学中合理利用知识导图，有利于学生明晰知识重点，理清知识间的关系，完善知识体系. 上述课堂教学中多次借助知识导图指导学生总结归纳，如“直线的倾斜角”的探究中，利用知识导图归纳直线的几何要素，梳理“点”和“方向”的内在联系;“直线的斜率”的探究中，构建倾斜角、方向、斜率之间的相互关系，强化学生理解直线方向的刻画. 但实际教学中运用知识导图时要注意两点，一是知识的总结，建议让学生自行归纳;二是导图结构的简练，内在联系的明确，建议引导学生在日常学习中多练.

3. 设问引导探究，综合能力提升

教学设计建议采用“设问引导，过程探究”的方式，即围绕知识重点合理设计引导性问题，让学生自主思考、猜想，得到结论，提升学生的数学思维和探究能力. 以上述章节教学为例，针对教学内容设计三大探究环节，每一个环节结合操作实践，设问引导学生逐步感知概念，生成定义知识等. 教学中设问引导要注意两点，一是问题设计要具有层次性、递进性，逐步深入探究主题;二是问题设计要充分围绕知识核心，合理设置问题背景.

写在最后

“直线的倾斜角与斜率”作为解析几何板块的重要知识内容之一，探究教学中要充分解读知识背景，明确核心内容，结合教学目标与重点来设置探究环节，引导学生积极参与课堂讨论，完成知识生成、总结归纳，让学生掌握知识的同时提升能力.

作者简介：张恩林（1993—），硕士研究生，中学一级教师，从事高中数学教学与研究工作，曾获苏州市微课比赛三等奖.