比赛场域下的中学数学教师说题内涵及策略

[摘 要] 教师教研比赛场域下的说题活动，能有效展现说题教师优良的数学专业素养和较高的课堂教学驾驭能力. 文章以2023年高考数学新课标Ⅰ卷第22题的说案设计为例，借“题”发挥，品读高考真题，深度剖析说题结构、说题设计及说题策略，揭示素养导向下教师教研比赛中说题的内涵及策略，助推落实学科育人和中学数学教师专业成长.

[关键词] 教研比赛;说题策略;高考真题品读;专业成长

教研比赛场域下的说题活动，是基于教研机构和学校教师广泛运用的说题教研方式，能有效遴选具有优良数学专业素养和较高课堂教学驾驭能力的教师. 说题教师在备题（命题研究、解题研究）的基础上，“以语言为主要表述工具，以课堂教学为背景，以数学课程标准和现代教育理论为指导，面向同行和专家，系统而概括地解说对一道数学题的教学理解，阐述具体传授某道题的教育设想、方法策略和组织教学的理论依据，分析学生学题时的已有基础、学习障碍和典型问题，并根据听者的建议进行反思改进的教研活动”[1]. 通过说题，教师展现自身数学教育的理论功底、数学知识的掌握程度、数学方法的理解能力及数学教学的前瞻性理念[2]，综合体现理解数学、理解学生、理解教学等能力水平. 说题是一种进阶认知思维的活动，对教师的专业素养的要求较高，同时也有促进作用. 笔者以2023年高考数学新课标Ⅰ卷第22题的说案设计为例，借“题”发挥，品读高考真题，深度剖析、揭示说题的内涵及策略，推动学科育人和中学数学教师专业发展.

说题结构

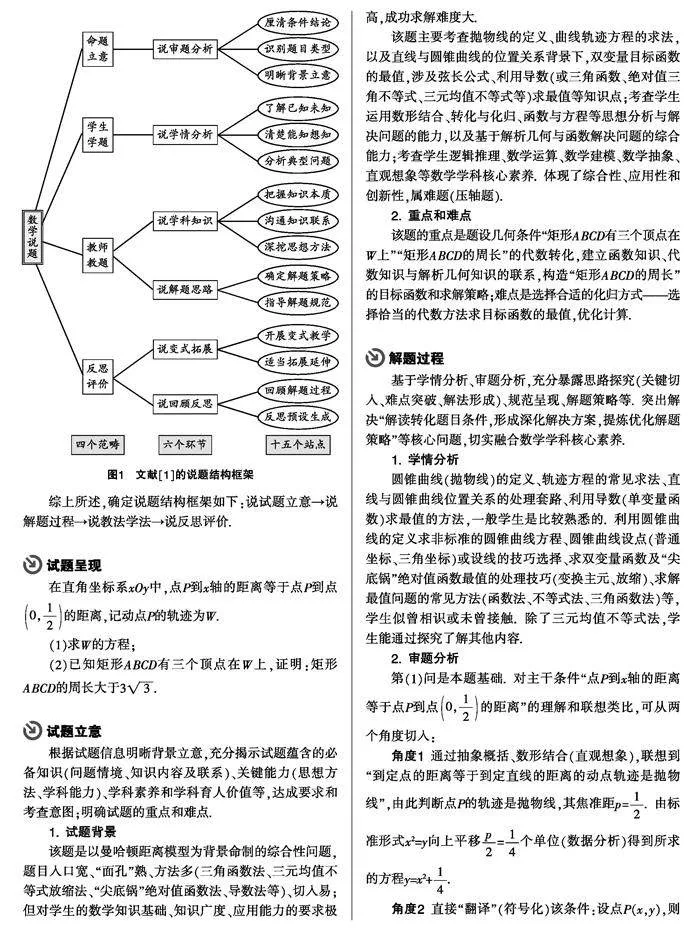
若以说题基本流程为明线，以核心素养的落实为暗线，则能为没有基本模式的说题添上“思维的隐形翅膀”[3]. 为使说案设计有章可循，可以制定大致的说题结构框架. 文献[1]给出了系统性的说题结构框架，包含“四个范畴”“六个环节”及“十五个站点（监测点）”，如图1所示. 实际上，说题比赛（教研）活动通常只有10～15分钟，因此说题需根据说题素材的特点，基于图1的结构框架有机整合、有所侧重.

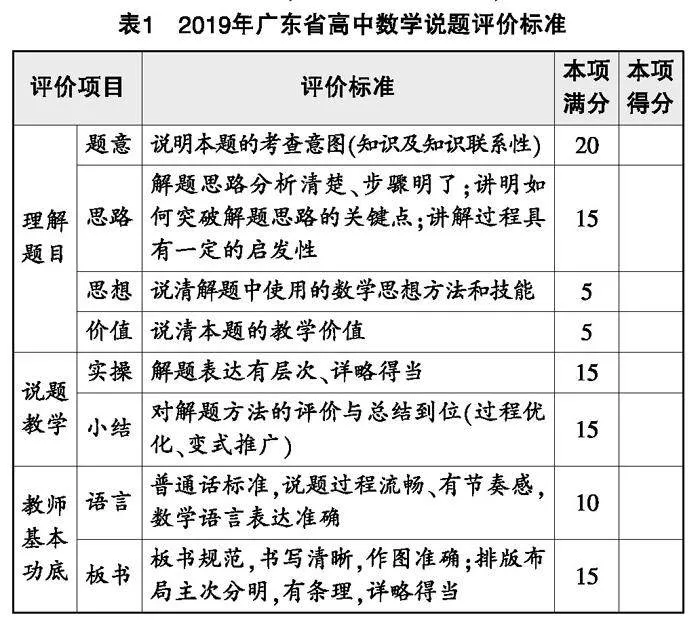
基于说题评价标准，也可以对标整合，如表1所示.

综上所述，确定说题结构框架如下：说试题立意→说解题过程→说教法学法→说反思评价.

试题呈现

在直角坐标系xOy中，点P到x轴的距离等于点P到点0，的距离，记动点P的轨迹为W.

（1）求W的方程;

（2）已知矩形ABCD有三个顶点在W上，证明：矩形ABCD的周长大于3.

试题立意

根据试题信息明晰背景立意，充分揭示试题蕴含的必备知识（问题情境、知识内容及联系）、关键能力（思想方法、学科能力）、学科素养和学科育人价值等，达成要求和考查意图;明确试题的重点和难点.

1. 试题背景

该题是以曼哈顿距离模型为背景命制的综合性问题，题目入口宽、“面孔”熟、方法多（三角函数法、三元均值不等式放缩法、“尖底锅”绝对值函数法、导数法等）、切入易;但对学生的数学知识基础、知识广度、应用能力的要求极高，成功求解难度大.

该题主要考查抛物线的定义、曲线轨迹方程的求法，以及直线与圆锥曲线的位置关系背景下，双变量目标函数的最值，涉及弦长公式、利用导数（或三角函数、绝对值三角不等式、三元均值不等式等）求最值等知识点;考查学生运用数形结合、转化与化归、函数与方程等思想分析与解决问题的能力，以及基于解析几何与函数解决问题的综合能力;考查学生逻辑推理、数学运算、数学建模、数学抽象、直观想象等数学学科核心素养. 体现了综合性、应用性和创新性，属难题（压轴题）.

2. 重点和难点

该题的重点是题设几何条件“矩形ABCD有三个顶点在W上”“矩形ABCD的周长”的代数转化，建立函数知识、代数知识与解析几何知识的联系，构造“矩形ABCD的周长”的目标函数和求解策略;难点是选择合适的化归方式——选择恰当的代数方法求目标函数的最值，优化计算.

解题过程

基于学情分析、审题分析，充分暴露思路探究（关键切入、难点突破、解法形成）、规范呈现、解题策略等. 突出解决“解读转化题目条件，形成深化解决方案，提炼优化解题策略”等核心问题，切实融合数学学科核心素养.

1. 学情分析

圆锥曲线（抛物线）的定义、轨迹方程的常见求法、直线与圆锥曲线位置关系的处理套路、利用导数（单变量函数）求最值的方法，一般学生是比较熟悉的. 利用圆锥曲线的定义求非标准的圆锥曲线方程、圆锥曲线设点（普通坐标、三角坐标）或设线的技巧选择、求双变量函数及“尖底锅”绝对值函数最值的处理技巧（变换主元、放缩）、求解最值问题的常见方法（函数法、不等式法、三角函数法）等，学生似曾相识或未曾接触. 除了三元均值不等式法，学生能通过探究了解其他内容.

2. 审题分析

第（1）问是本题基础. 对主干条件“点P到x轴的距离等于点P到点0

，的距离”的理解和联想类比，可从两个角度切入：

角度1 通过抽象概括、数形结合（直观想象），联想到“到定点的距离等于到定直线的距离的动点轨迹是抛物线”，由此判断点P的轨迹是抛物线，其焦准距p=. 由标准形式x2=y向上平移=个单位（数据分析）得到所求的方程y=x2+.

角度2 直接“翻译”（符号化）该条件：设点P（x，y），则=y

，化简得y=x2+，即W的方程.

上述两个角度体现了逻辑推理、数学运算、数学抽象、直观想象和数据分析核心素养.

第（2）问是本题核心，考查知识、能力、素养的延伸和深化. 如图2①所示，对显性条件“矩形ABCD有三个顶点在W上”和隐性条件“AB⊥AD”，以及问题目标“矩形ABCD周长的最小值，即2（AB+AD）的最小值”的挖掘和代数转化是关键. 需要思考三个问题.

[③]

问题1 （宏观目标导向）从问题目标来看，“求最值问题”是从几何的角度切入，还是从代数（函数、不等式等）的角度切入？显然，本题适合从代数（函数、不等式等）的角度切入，构造目标“求2（AB+AD）的最小值”. 常见的处理方法有以下几种：若目标函数为三角函数，则利用正弦和余弦的有界性求最值;若目标函数为一般函数，则利用函数图象或导数求最值;若目标函数为多元函数，则考虑用不等式法（囿于所学知识，考虑二元均值不等式类型）求解.

问题2 （中观方案探究）从已知条件来看，三个动点的坐标未知，如何引入适量的未知数便于运算求解？涉及“设点”“设线”技巧的选择. 思路1：“设点法”，即设三个动点的坐标，从而代数化求解. 思路2：“设线法”，即设A点的坐标和直线AB，AD的斜率，列出直线AB，AD的点斜式方程，从而代数化求解.

问题3 （微观运算优化）基于“A，B，D的坐标均为未知量”和目标“AB，AD

两条线段的表示”，如何简化模型建立中的运算？其一，研究“已知条件”与“问题目标”的沟通桥梁“AB⊥AD”，易发现直线AB与AD的特殊位置关系使其方程（形式相同，斜率不同），B与D两点的坐标（相对点A旋转90°），AB与AD的表示式（算理相同、结构相同，仅斜率或某一坐标不同）均保持相应规律（算理）一致性. 因此，在由两点间的距离公式（较适合“设点法”）或弦长公式（较适合“设线法”）建立目标函数模型的过程中，使用“同构”和“同理”的方法可以实现“求一得二”的效果. 其二，基于抛物线平移2（AB+AD）的不变性，可将抛物线平移至图2②或图2③所示的位置优化运算.

上述三个问题体现了逻辑推理、直观想象、数学建模、数学抽象和数学运算核心素养.

3. 思路探究

（1）建立目标函数

思路1 “设线法”.

解法1 基于图2①，设Aa，a2+，直线AB：y=k（x-a）+a2+，与抛物线y=x2+联立，消除y并化简得x2-kx+ka-a2=0，其根为x，x，易得x=k-a. 由于矩形ABCD的顶点不能重合，因此x≠x，x≠x⇒k≠2a，所以k≠-. 由弦长公式可得

基于图2②，设A（a，a2），直线AB：y=k（x-a）+a2，与抛物线y=x2联立，消除y并化简得x2-kx+ka-a2=0，其根为x，x. 其他同上，略.

基于图2③——将图2①中的抛物线y=x2+按=-a，-a2

-进行平移，设A（0，0），抛物线为y+a2+=（x+a）2+，即y=x2+2ax. 直线AB：y=kx，与抛物线y=x2+2ax联立，消除y并化简得x2+（2a-k）x=0，其根为x=0，x=k-2a. 其他同上，略.

基于图2①为通法，图2②、图2③需理解向量平移的本质及规律，通过批判性思维、迁移创新和灵活运用，简化运算.

思路2 “设点法”.

4. 规范呈现

为指导学生审题、解题和作答，培养学生良好的解题习惯，规范呈现解法1、解法3的解答过程（内容略）.

5. 解题策略

基于波利亚在《怎样解题》中提出的“理解题目、拟订方案、执行方案和回顾与反思”的解题策略，从学生的知识基础、解题经验着手，从宏观目标导向、中观方案探究、微观运算优化等角度审视解题思路;利用变换主元法、放缩消元法、整体代换法、导数法等方法技巧，以及数形结合、逆向思维、分类讨论、函数与方程、转化与化归等思想策略，对目标函数变形求解.

教法学法

从学情分析出发，围绕难点突破、解法溯源、过程优化、合作探究、素养培养等核心点进行阐述.

1. 问题驱动

立足学生认知水平及答题难点等学情，通过三个问题（见上述“审题分析”中的三个问题内容）引导学生建构解决问题的思维基本框架，先整体再局部，“见树木”更“见森林”.

2. 难点突破

分析学生存在的问题，针对解法难点和新增经验点（如“尖底锅”图象、绝对值三角形不等式、平移的不变性等），引导学生合作探究. 在学生的最近发展区内详细解析，提炼二级结论，促进学生积累基本活动经验.

3. 解法溯源

基于抛物线平移前后的位置状态，运用代数（函数）方法处理矩形ABCD周长双变量函数最值问题的策略丰富多样. 基于解法溯源厘清各种思路，搞清楚问题本质和所学知识的关系，正本清源，条分缕析，进一步优化过程及方法，实现“多法归一”，知识经验结构化.

反思评价

回顾解题过程，通过变式延伸，“再认识”解题活动，强化“元认知”，深化知识理解，把握问题本质，提升解题能力.

1. 回顾解题过程

本题综合运用直线与圆锥曲线的位置关系知识求最值，入口宽、解法多，有难度且新颖. 试题的解决过程体现了常用的数学思想方法，以及解题技巧和工具，如变换主元法、放缩消元法、导数法和绝对值三角不等式等，考查学生必备知识（代数与几何、函数等主线知识）、关键能力（逻辑推理能力、数学建模能力、数学抽象能力、运算求解能力、直观想象能力等）、核心素养（逻辑推理、数学运算、数学建模、数学抽象、直观想象等）.

2. 变式延伸

以原题为源，深入挖掘并延伸题目，助力备考. 基于本题，可做如下变式拓展.

变式题1 （根据1998年上海竞赛题改编）本题（2）中，若将“矩形ABCD有三个顶点在W上”改为“正方形ABCD的A，B，C三个顶点在W上”（其他条件不变），试求：（1）正方形ABCD面积的最小值;（2）·的最小值.

变式题2 （根据2023年广州市高三二测试题改编）在平面直角坐标系xOy中，定义d（A，B）=

为A（x，y），B（x，y）两点之间的“折线距离”（也叫曼哈顿距离）. 已知M是曲线y=上任意一点，N是直线y=-x+上任意一点，则d（M，N）的最小值为______.

说题策略

说题活动能有效、充分展现教师的学科专业素养、教学组织和管理能力等. 高质量的说题活动，遵循“四个视角”：从命题者的视角去理解数学题，从专业理论的视角去审视数学题，从学生解题的视角去讲解数学题，从反思的视角批判和感悟解题过程. 同时，要反思日常教学：立足基础，揭示本质，强化联系，挖掘思维，拓展延伸，发展学生的数学学科核心素养.

参考文献：

[1] 洪梦，吴立宝，王富英. 数学说题的内涵与结构[J]. 数学通报，2020，59（11）：58-63.

[2] 傅瑞琦. 说题，让主题教研更精彩：一次教师说题主题教研活动的策划、组织与思考[J]. 中国数学教育，2012（5）：45-48.

[3] 卫小国，王进军. 核心素养整体观下的说题[J]. 中学数学，2018（1）：83-86.

作者简介：吴光潮（1979—），中学高级教师，从事中学数学教育教学工作.