基于GGInformer模型的金融数据特征提取及价格预测

摘要： 为了解决金融时序预测任务中出现的特征参数冗余问题，用遗传算法对金融数据进行特征提取，通过三组对比实验进行验证分析。实验结果显示，加入了遗传算法的预测模型比未加入遗传算法的模型在三种数据集上的MSE均有所降低。最终结果证明遗传算法可以有效解决金融产品价格预测过程中的特征冗余问题。为了解决非线性的长序列金融数据预测效果差的问题，通过结合GRU网络和Informer模型构建了GGInformer模型来对金融产品价格进行预测。模型在三种外汇产品数据集上与其他四种预测基准方法进行了对比实验，实验结果与可视化分析表明，所提模型在金融产品交易价格的预测结果上有明显优势，可以提高预测的精度。

关键词： 遗传算法； 特征提取； 金融产品价格预测； Informer模型； GRU网络

中图分类号： TP183

文献标志码： A

文章编号： 1671-6841（2024）05-0062-09

DOI： 10.13705/j.issn.1671-6841.2023125

Feature Extraction and Price Prediction of Financial Data Based on

GGInformer Model

REN Shengqi， SONG Wei

（School of Computer and Artificial Intelligence， Zhengzhou University， Zhengzhou 450001， China）

Abstract： In order to solve the problem of redundant feature parameters in financial time series prediction tasks， genetic algorithm was selected to extract features from financial data. Three sets of comparative experiments were conducted to verify and analyze the results. The experimental results showed that the prediction model with genetic algorithm added had lower MSE results than the model without genetic algorithm on three datasets. The final results showed that genetic algorithms could effectively solve the problem of feature redundancy in the process of predicting financial product prices. In order to solve the problem of poor prediction performance of nonlinear long sequence financial data， a GGInformer model was constructed by combining GRU network and Informer model to predict financial product prices. The model was compared with four prediction benchmark methods on three foreign exchange product datasets. The experimental results and visual analysis showed that the model had significant advantages over other prediction models in predicting the trading prices of financial products， and could improve the accuracy of prediction.

Key words： genetic algorithm; feature extraction; financial product price prediction; Informer model; GRU network

0 引言

金融产品价格变化是大众关注的焦点，与之相关的预测问题也是一个令人关注和富有挑战性的研究课题。

传统时序建模方法主要依靠统计学理论进行金融市场趋势预测。早期研究者基于统计学方法来描述金融市场变化情况，Engle［1］提出自回归条件异方差模型，否定了线性假设风险与收益之间的关系，能够更好地描述金融价格变动。Airyo等［2］提出的差分整合移动平均自回归模型（ARIMA）被应用于股价的预测。上述方法对数据分布规则和完整性等方面要求严格，但是金融市场本身是一个非线性、非平稳、多尺度的时间序列，存在很多噪声，这使得传统时序预测方法无法得到较高的预测精度。

鉴于传统统计学方法的局限性，有研究人员将信号处理方法应用于金融预测。Ramsey等［3］首次将小波变换应用于量化投资领域，用来检测突变点和跳跃点。Huang等［4］提出EEMD改进算法应用于金融分析。Wu等［5］构建CEEMD-A&S-SBL模型应用于金融预测。

随着深度学习技术在特征提取和构建复杂非线性模型上取得了巨大进展，研究人员开始基于深度学习技术进行金融产品交易价格预测研究。姚宏亮等［6］将贝叶斯神经网络和均线滞后特征结合，提出了用于股市态势预测的DSMA模型，通过实验证明了模型的预测效果。Meesad等［7］使用支持向量回归模型对股票数据进行建模分析。Nair等［8］提出了一种基于粗糙集的决策树系统，该方法对孟买证券交易所数据进行了研究，使用C4.5决策树和粗糙集进行特征提取和规则总结。Selvin等［9］使用CNN、RNN和LSTM算法对股票市场进行预测。姜振宇等［10］通过结合变分模态分解和时序卷积神经网络构建了时频融合的卷积神经网络模型，并通过实验证明了模型具有良好的预测精度。杨妥等［11］提出了融合情感分析的SVM-LSTM模型，实现了对股指期货预测精度提高的目标。Zhang等［12］建立了CEEMD-LSTM模型，将该模型应用于金融时间序列预测中，并用实验证明模型精确度高且具有良好的鲁棒性。Ding等［13］通过引入高斯先验、正交正则化和交易间隙分配器优化了Transformer 股票预测模型。

尽管以上针对金融产品交易价格预测的方法已经取得了较好的结果，然而在处理特征参数冗余、非线性的长序列金融时序数据时仍然存在局限性。为解决金融数据特征冗余问题，本文采用遗传算法（genetic algorithm，GA）［14］对金融产品数据进行特征提取，选取出更具有竞争性的特征组合来消除冗余特征的影响。为了解决非线性、长序列的金融数据预测效果差的问题，本文结合门控循环单元（gate recurrent unit，GRU）网络［15］和Informer模型［16］构建GGInformer（GA GRU Informer）模型对金融产品价格进行预测。实验结果表明，GGInformer 模型可以有效地对金融数据进行价格预测。

1 方法构建

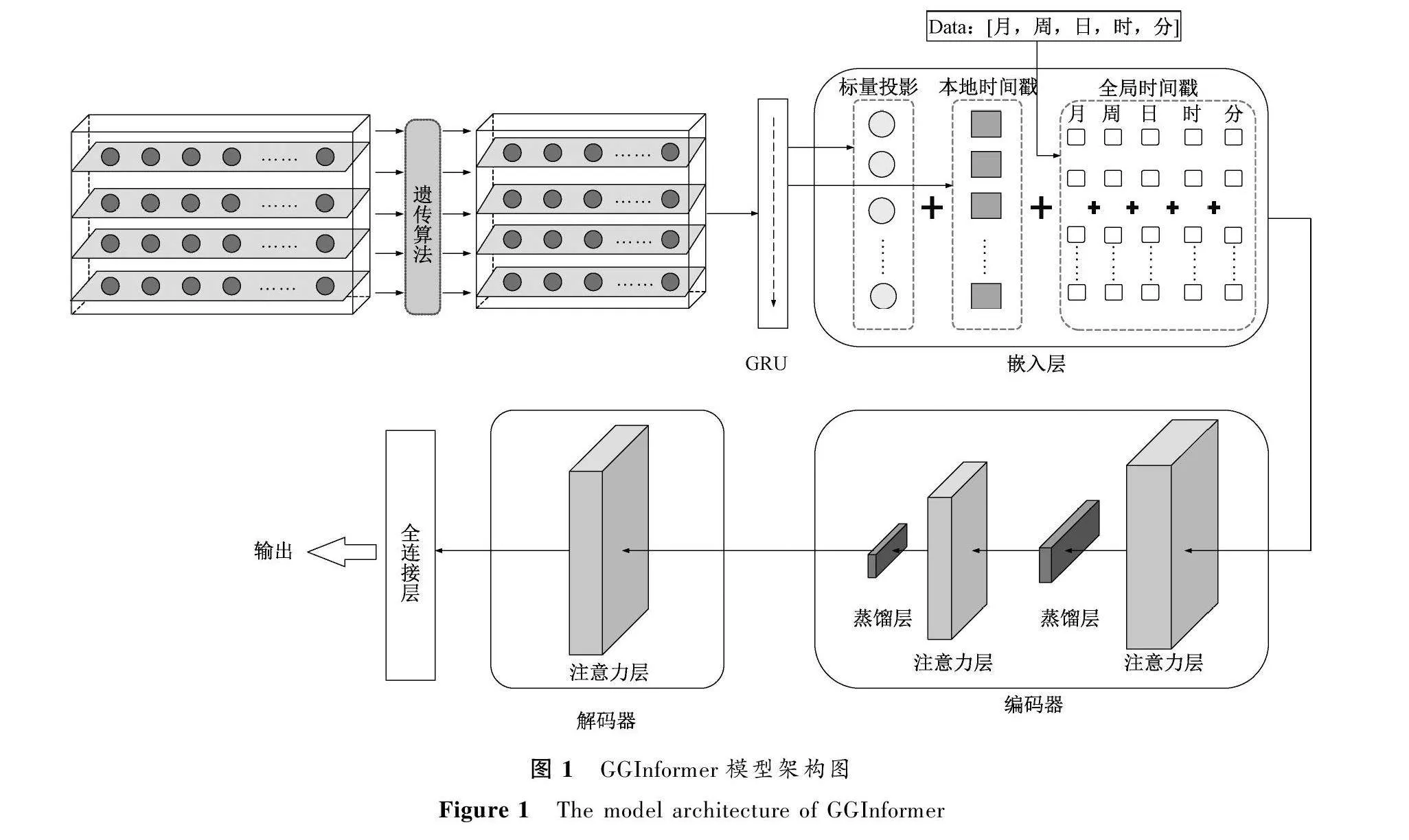
本文结合遗传算法、GRU网络和Informer模型构建了GGInformer模型，以此对金融产品数据进行特征提取以及交易价格预测。首先使用遗传算法对金融产品数据进行特征提取，可以减少冗余特征对后续预测过程的影响，同时还可以减少输入预测模型中的数据，起到降低计算量的作用。然后将特征提取后的数据输入GRU网络，进一步提取金融数据的全局依赖信息。之后将GRU网络的输出数据输入Informer 模型，经过嵌入层、编码器和解码器，最后经过一个全连接层得到预测值。GGInformer模型架构图如图1所示。

1.1 基于遗传算法的特征选择方法构建

由于金融产品数据价格预测需要依赖大量的特征参数，但是通常不是全部的特征都对最终的预测产生积极的影响，因此金融产品数据价格预测往往存在特征冗余的问题。为解决此问题，本文使用遗传理论中优胜劣汰的法则提取具有竞争性的特征组合来消除冗余特征对预测效果的影响。遗传算法基本的操作包括基因编码、产生初代种群、染色体选择、染色体交叉、染色体变异，不断产生新的子代以寻找最优解。

1） 种群初始化。本文对输入的金融产品数据采用二进制编码进行种群初始化，每条数据的每一个特征因子位按照等概率在{0，1}中选择。用矩阵表示为

a1，x1…a1，xn

am，x1…am，xn，

其中：xj（j=1，2，…，n）代表数据特征；ai，xj（i=1，2，…，m）∈{0，1}，值为0时表示未被选中，值为1时表示被选中；m为时序数据的长度。

2） 适应度函数选取。本文选择基于类内、类间距离的可分性判断依据作为适应度函数。

假设从D个特征中选出d个最优的特征（d<D），定义为

Sb=∑ci=1Pi（hi-h）（hi-h）T，（1）

Sw=∑ci=1Pi1qi∑qik=1（x（i）k-hi）（x（i）k-hi）T，（2）

Jd（x）=trSbtrSw，（3）

式中：c为样本数；qi为第i类样本数；hi表示样本集的均值向量；h表示所有各类的样本集总均值向量；Pi为i类的先验概率；x（i）k为第i类的D维特征向量；Sb为类间离散度矩阵；Sw为类内离散度矩阵；trSb、trSw表示求两个矩阵的迹。

3） 选择算子选取。确定了适应度函数之后，遗传算法基于适应度值对个体进行评价，本文使用轮盘赌方法作为选择算子。

4） 交叉算子选取。本文采用多点交叉方式作为交叉算子。在单个个体中随机设置多个交叉点，两个个体间根据交叉点进行基因交换，生成新的个体。

5） 变异算子选取。本文采用单点位翻转突变作为变异算子。从种群中随机选择一个个体，再随机从个体基因中选择一个基因进行翻转变异。基于遗传算法的特征选择过程如算法1所示。

算法1 基于遗传算法的特征选择

输入：特征选择前的高维金融数据P∈Rl×m。

输出：特征选择后的低维金融数据Best∈Rl×n。

1） 初始化（P（t））；

2） 计算适应度函数（P（t））；

3） 取最优解（P（t））；

4） While 是否满足终止条件？ do

5） P（t）←遗传选择（P（t））；

6） P（t）←遗传交叉（P（t））；

7） P（t）←遗传变异（P（t+1））；

8） 计算适应度函数（P（t））；

9） 取最优解（P（t））；

10） t=t+1；

11） end。

1.2 基于GGInformer模型的预测方法构建

由于金融产品价格预测任务需要预测长时间段的时间序列，为了增强后续的预测效果，本文选择GRU网络进行时序数据的全局信息提取，通过GRU网络可以增强时序数据间的时序依赖关系。GRU网络有三层，后面继续构造两层线性层，之后将输出结果输入Informer模型进行预测。

为了解决金融产品价格预测这类序列很长的问题，模型需要具有较强解决长程依赖问题的能力。本文选择Informer模型来对金融数据的价格进行预测。模型结构主要包括嵌入层、编码器、解码器和全连接层。

嵌入层包括三部分，分别为标量投影嵌入、本地时间戳嵌入和全局时间戳嵌入，嵌入层可为输入数据添加位置向量，以及每个时间点的时间信息。其中标量投影嵌入主要采用一维卷积将输入数据的特征维度向量转换为512维向量。本地时间戳嵌入采用Transformer模型［17］中的位置编码方法。全局时间戳嵌入采用全连接层将输入的时间戳向量映射为512维向量。最后将标量投影嵌入、本地时间戳嵌入和全局时间戳嵌入三者结果相加得到最终的嵌入层结果。

编码器包括两部分，分别为自注意力层和蒸馏层。自注意力层Informer模型使用算法2描述的概率稀疏自注意力机制。

算法2 概率稀疏自注意力机制

输入：Tensor Q∈Rm×d，K∈Rn×d，V∈Rn×d。

输出：概率稀疏自注意力特征矩阵S。

1） 设置超参数c，u=clnm，U=mlnn；

2） 从K中随机采样U个点积对作为K；

3） 计算采样的得分S=QKT；

4） 按行计算稀疏性得分

M=max（S）-mean（S）；

5） 按照M排名选择前u个Qi作为Q；

6） 计算S1=softmax（QKT/d）·V；

7） 计算S0=mean（V）；

8） 计算S=｛S1，S0｝，调整为原来行顺序。

根据算法2介绍的概率稀疏自注意力计算得出的S必然会产生冗余（由于存在S0），因此在编码器中又加入了自注意力蒸馏机制，以此来蒸馏出更有优势的注意力权重。从第j层到j+1层的蒸馏计算为

Xtj+1=MaxPool（ELU（Conv1d（［Xtj］AB））），（4）

其中：［Xtj］AB包括了多头概率稀疏自注意力权重以及前馈层的关键操作；Conv1d表示在时间维度上执行一维卷积操作；ELU为激活函数；MaxPool函数为最大池化，可将输入的长度变为原来的一半，从而极大地节约了内存开销和计算时间。

解码器由一个掩码多头概率稀疏自注意力层和一个多头自注意力层组成。多头概率稀疏自注意力层要进行掩码操作，避免使当前时间数据都注意到下一个时间情况，防止自回归。解码器舍弃了动态解码过程，而采用一次前向过程，即可解码得到整个输出序列，大幅缩短了预测时间。需要注意的是，解码器使用的是生成式推理解码，其输入数据形式为

Xtde=Concat（Xttoken，Xt0）∈R（Ltoken+L0）×dmodel，（5）

其中：Xttoken∈RLtoken×dmodel是预测开始标签，对于推理预测提供推理依据，从编码器输入值中截取；Xt0∈RL0×dmodel是一个为预测序列保留的占位时序序列，填充值为0。

最后经过Informer模型解码器之后连接一个全连接层进行预测输出。

2 实验设计

2.1 数据集

为了验证本文所提方法对解决特征冗余、非线性的长序列金融数据预测问题的效果，本文选取三种外汇产品的真实历史数据用于实验，包括欧元兑美元汇率（EUR/USD）、原油兑美元汇率（USO/USD）、黄金兑美元汇率（XAU/USD）。三种数据集包括开盘价、最高价、最低价、收盘价、吞吐量、延迟量等特征因子。

由于数据特征间单位和尺度存在差异，对于模型后续训练可能产生影响。因此，为了消除影响，以及对每一维度特征进行平等处理，需要对数据特征进行标准归一化处理，将数据控制在［0，1］范围内。本文采用最大最小值标准化方法对数据进行处理，公式为

x^=x-min（x）max（x）-min（x），（6）

其中：x代表原特征序列数据；min（x）代表原特征序列最小值；max（x）代表最大值。

2.2 评价指标

依据实际需求，为了更加准确全面地评价模型效果，本文选择平均绝对误差（MAE）和均方误差（MSE）两种预测评价指标。所用公式为

MAE=1n∑nm=1（ym-y′m），（7）

MSE=1n∑nm=1（ym-y′m）2，（8）

其中：ym是真实值；y′m是预测值；n是测试集的长度。

2.3 对比模型与超参数设置

实验参数设置主要包括三部分：GRU网络隐藏层维度设置为64，GRU网络层数设置为三层；遗传算法中染色体长度设置为6，种群大小设置为50，变异概率设置为0.02，迭代次数设置为100；Informer模型有关参数设置中，嵌入层变换维度设置为512，编码器多头数设置为8，编码器层数设置为2，前馈层维度设置为2 048，概率稀疏注意力因子设置为5，dropout设置为0.05，激活函数为GELU，训练迭代次数设置为6，学习率设置为0.0001，损失函数设置为MSE。

3 实验分析

3.1 遗传算法特征选择结果分析

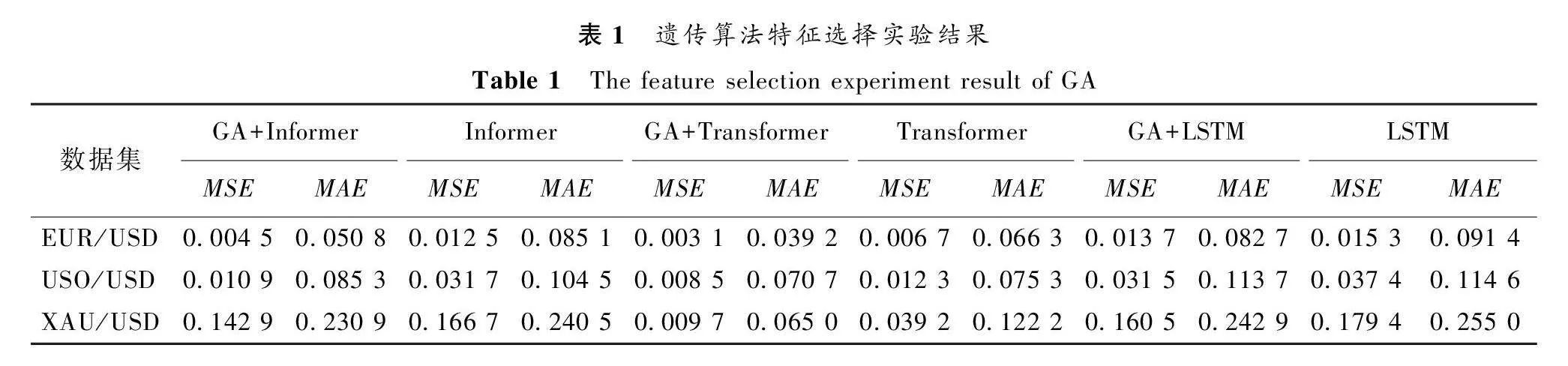
本文使用遗传算法对金融产品数据进行特征提取，选择出最优的特征组合进行预测实验。为了更准确地验证遗传算法的特征提取能力，本文选择金融预测领域应用较广泛的LSTM模型、Transformer模型和Informer模型作为预测模型进行对比试验，结果如表1所示，其中GA代表遗传算法。

根据表1中的结果可以看到，结合遗传算法的三种预测模型的实验结果均比未结合遗传算法的实验结果要好，尤其是Informer模型和Transformer模型对比结果更为明显。相比于Informer模型，GA+Informer模型在三种数据集上的MSE结果分别降低了64%，66%，14%；相比于Transformer模型，GA+Transformer模型在三种数据集上的MSE结果分别降低了54%，31%，75%；相比于LSTM模型，GA+LSTM模型在三种数据集上的MSE结果分别降低了11%，16%，11%。

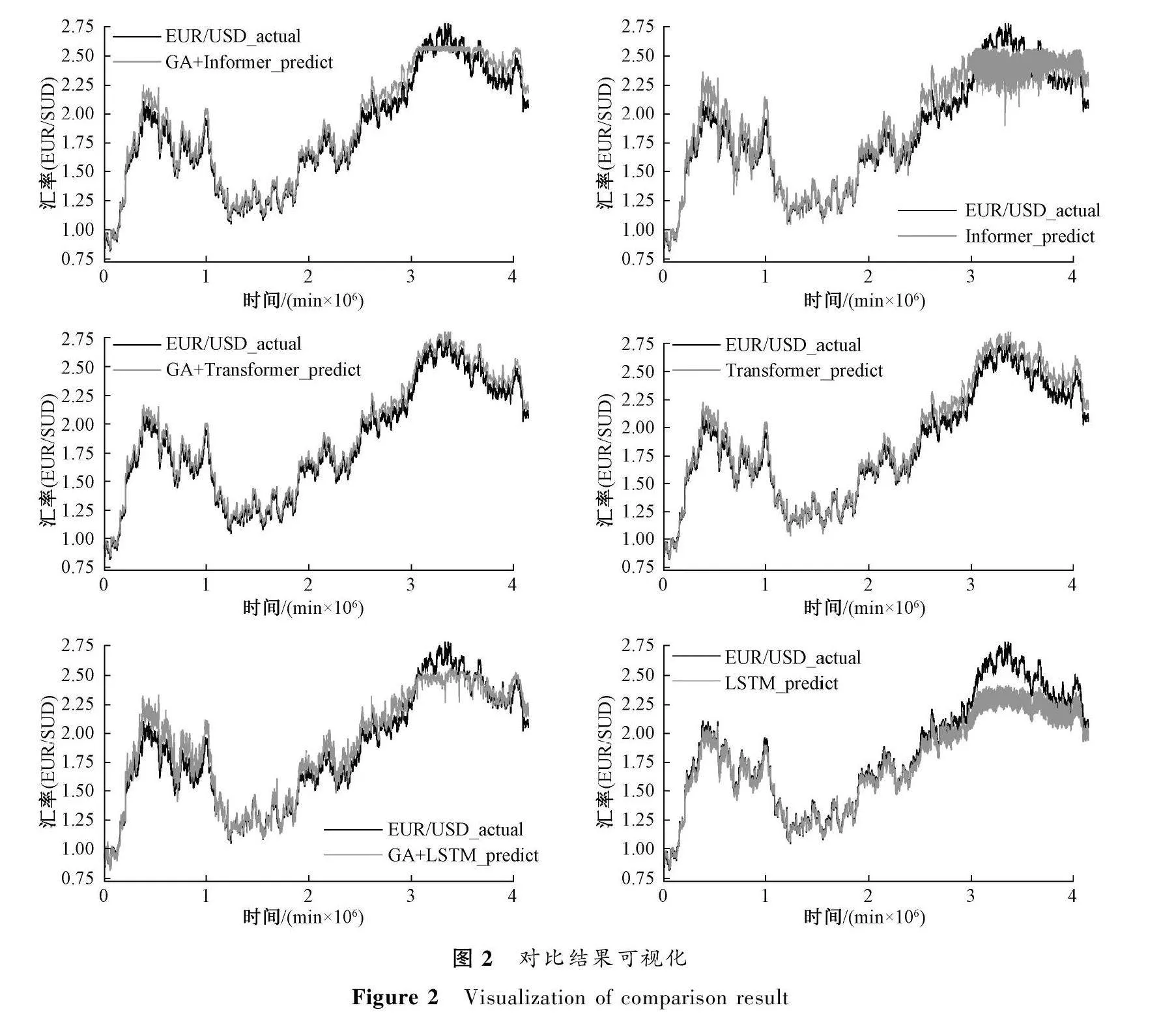
模型预测对比结果如图2所示（横坐标表示时间，纵坐标表示收盘时汇率）。从图2中也可以看到，经过遗传算法进行特征提取的预测结果比未使用遗传算法的预测结果更贴近真实值，而且结合遗传算法的模型预测结果变化较小，都是围绕在真实值附近，未使用遗传算法的模型预测结果波动较大，不能很好地贴合真实值。

上述对比结果说明竞争性较低的冗余特征会影响模型对结果的预测，通过遗传算法对输入的金融产品数据进行优势特征提取，对模型的预测效果可以起到积极作用。

3.2 GGInformer模型价格预测实验

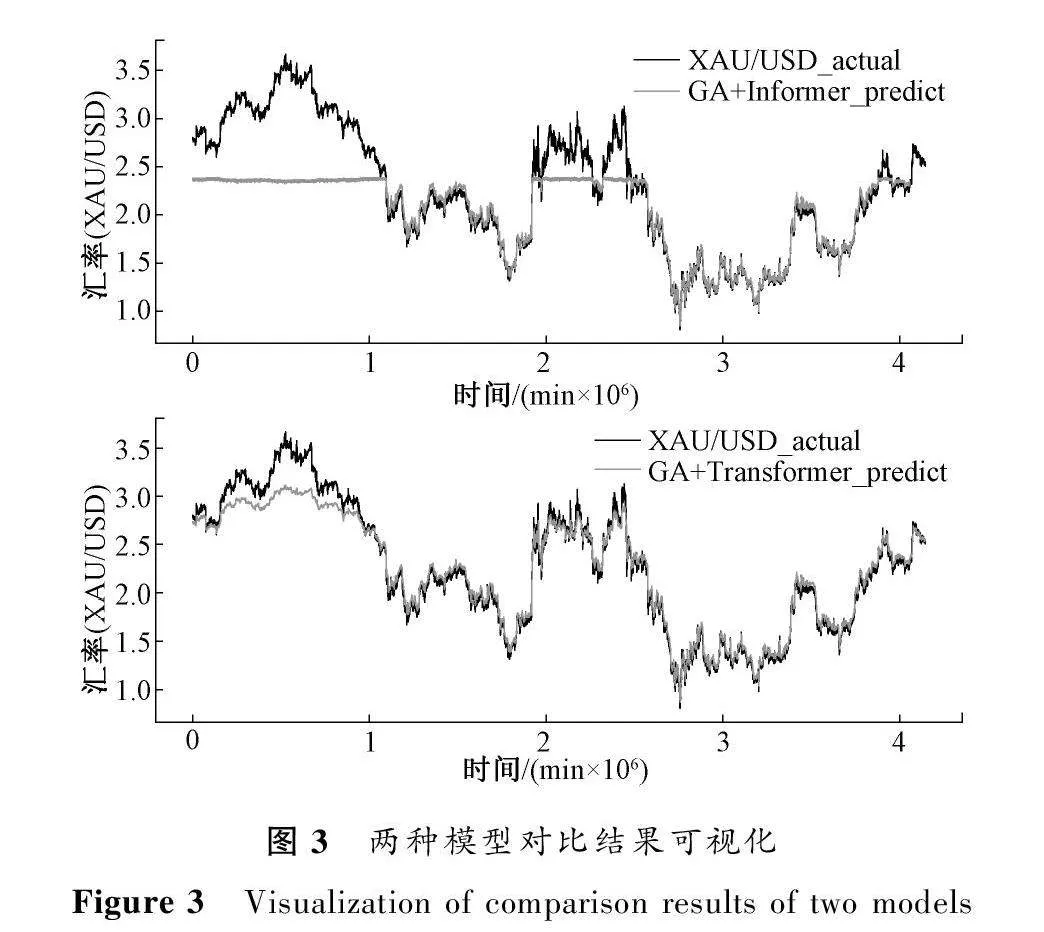
由表1可以看到GA+Informer模型和GA+Transformer模型在EUR/USD数据集和USO/USD数据集上结果相差不大，但是在XAU/USD数据集上结果却相差较大，本文对这一原因进行了分析。两种模型在XAU/USD数据集上的预测结果可视化如图3所示。

从图3可以看出，在XAU/USD数据集上，GA+Informer模型相比GA+Transformer模型来说，其对于价格较高部分的预测结果不太友好，而对于价格较低的部分却可以很好地预测。

通过对比图3中的两种模型，发现GA+Informer模型在训练初始阶段不能很好地学习到价格较高部分的趋势，导致后续高价格部分的预测结果较差，而GA+Transformer模型在初始阶段对于价格较高部分虽然也不能很充分地学习，但是相比GA+Informer模型可以学习到基本的价格趋势，因而对后续较高价格部分也可以有效地训练学习。

将上述情况结合其余两种数据集进行分析发现，GA+Informer模型对其余两种数据集同样不能很好地预测高价格的部分。同时发现其余两种数据集在前期训练时价格变化趋势是缓慢的，而XAU/USD数据集的价格变化起伏较大，且由于Informer模型是生成式预测，对于预测之前给定的用于推理预测的数据要求不能起伏变化太大，以免推理预测过程中找不到规律，导致预测结果较差。而Transformer模型则由于多步预测而不会出现这种问题。

为了解决上述问题，本文引入了GRU网络构建GGInformer模型来对金融价格进行预测。由于GRU网络可以更好地捕捉时序数据中时间距离较大的依赖关系，对于随着时间增长变化起伏较大的数据可以更好地记录依赖关系，有助于后续生成式预测。

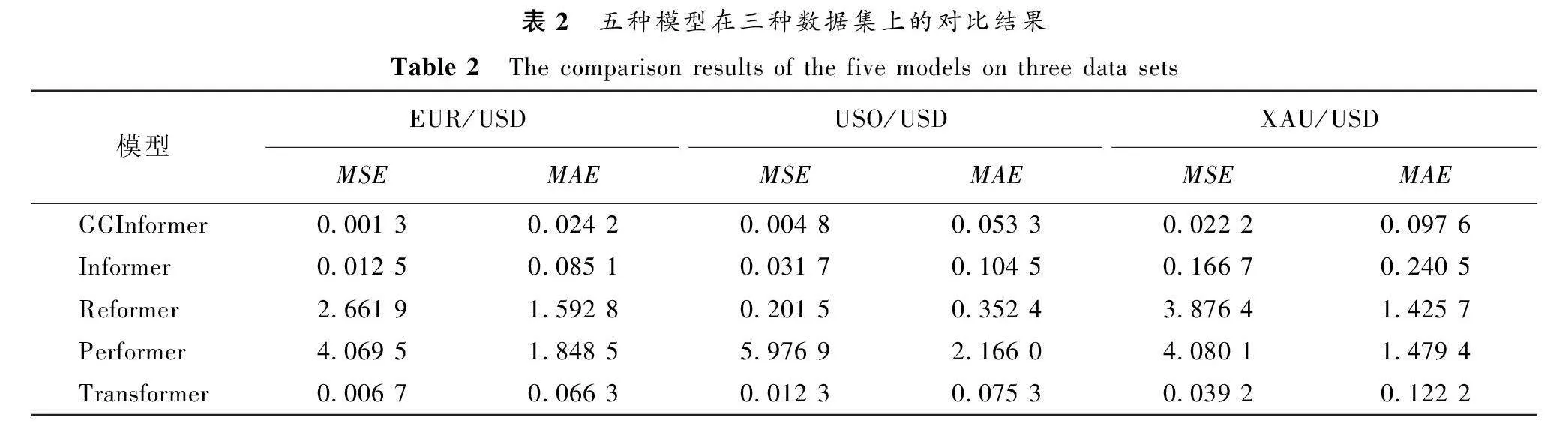
为了验证模型的效果，本文选择Informer、Reformer［18］、Performerih25vTmeaMGChNRCAGNK/g==［19］和Transformer模型作为基准模型，几种模型都可以兼顾模型效果和训练效率。用这四种模型与GGInformer模型进行对比来验证模型针对金融产品交易价格预测问题的有效性，所有模型均以收盘价为预测指标，并取两次收盘价预测结果的均值作为最终对比结果，所有预测模型均采用交叉验证的方式进行实验。GGInformer模型与其他四种预测模型的对比实验结果如表2所示。从表2可以看出，GGInformer模型与其他四种预测模型相比优势较为明显。相比于Informer模型，GGInformer模型在EUR/USD数据集上的MSE结果降低了90%；在USO/USD数据集上的MSE结果降低了85%；在XAU/USD数据集上的MSE结果降低了87%。说明该模型在实际金融预测场景下具有良好的表现。

需要说明，在表2中虽然Transformer模型与Informer模型相比预测效果要好，但是通过理论分析和具体实验证明，Informer模型要优于Transformer模型，尤其是对于金融时序预测任务这种具有长序列时序预测要求的任务，综合考虑，最终选择Informer模型作为金融预测任务的基准模型。

3.3 消融实验

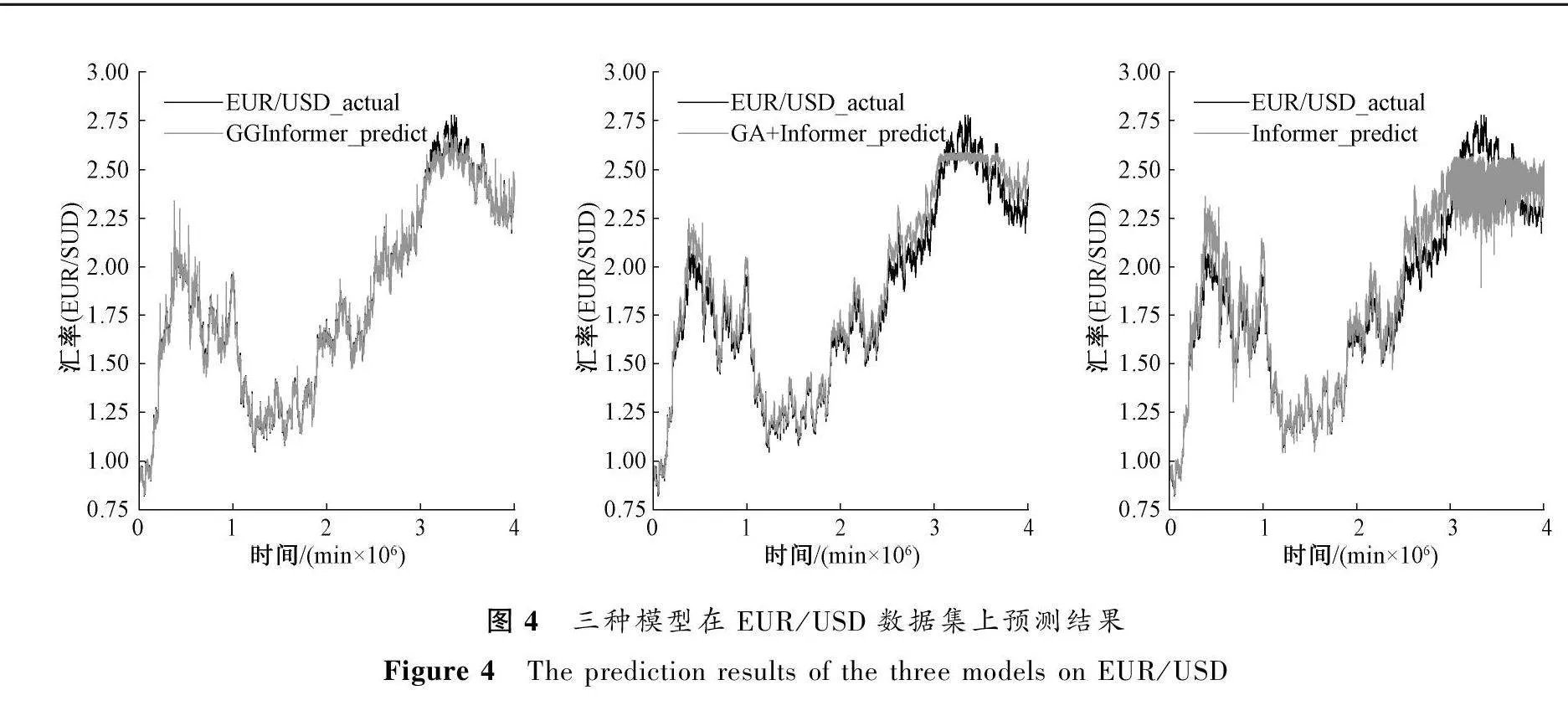
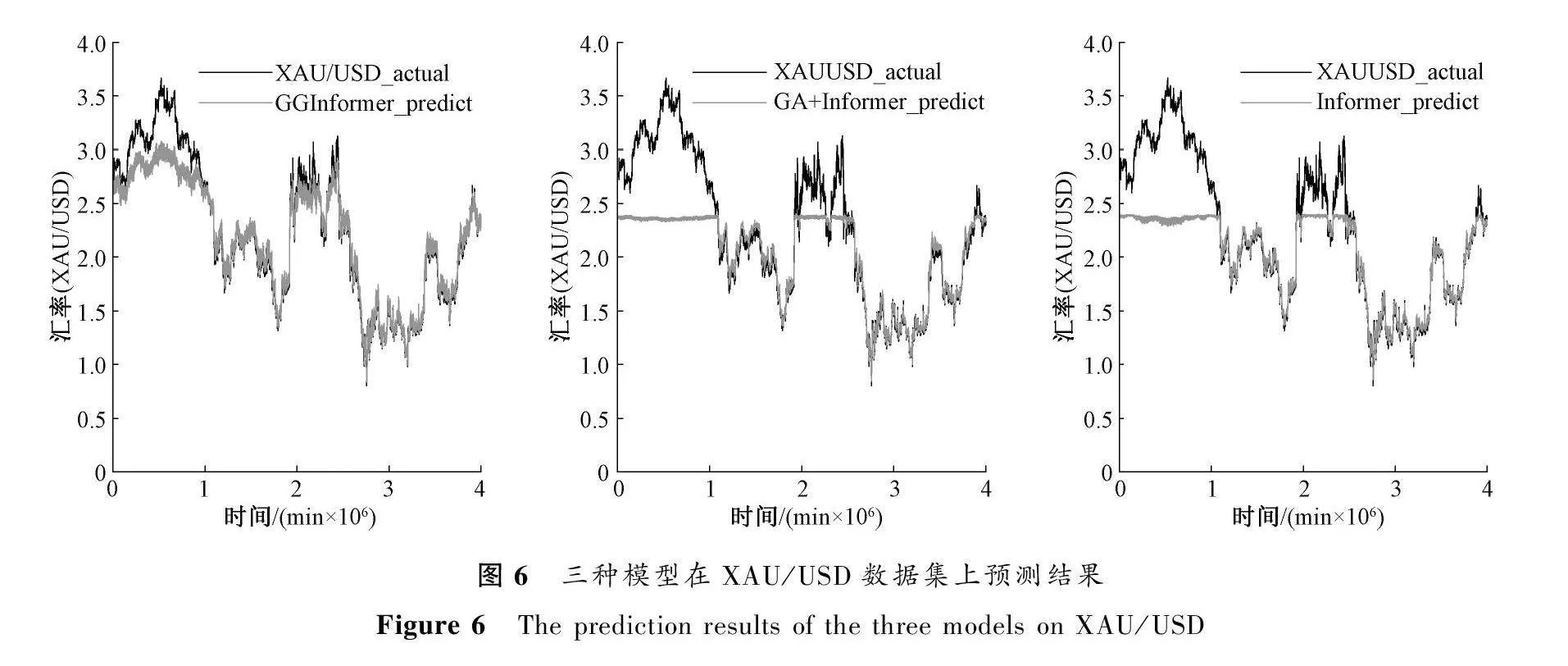
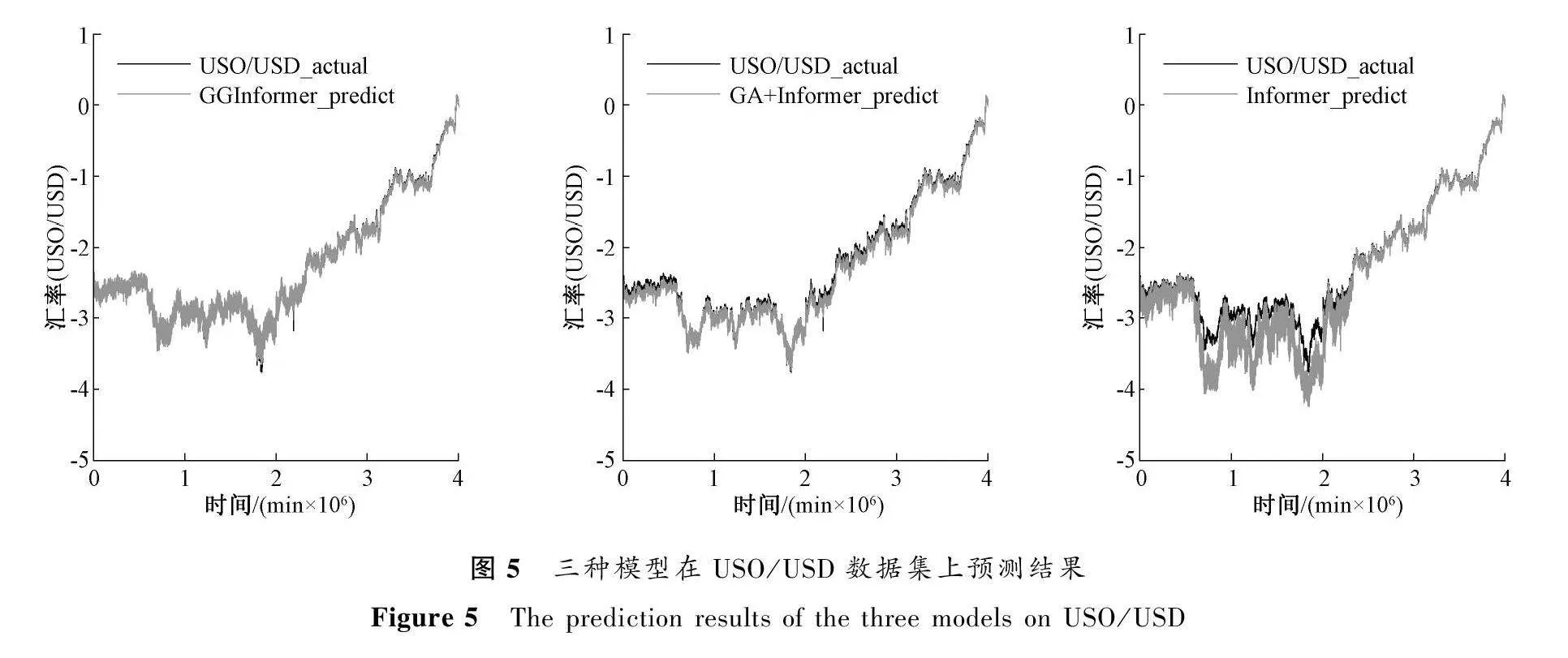
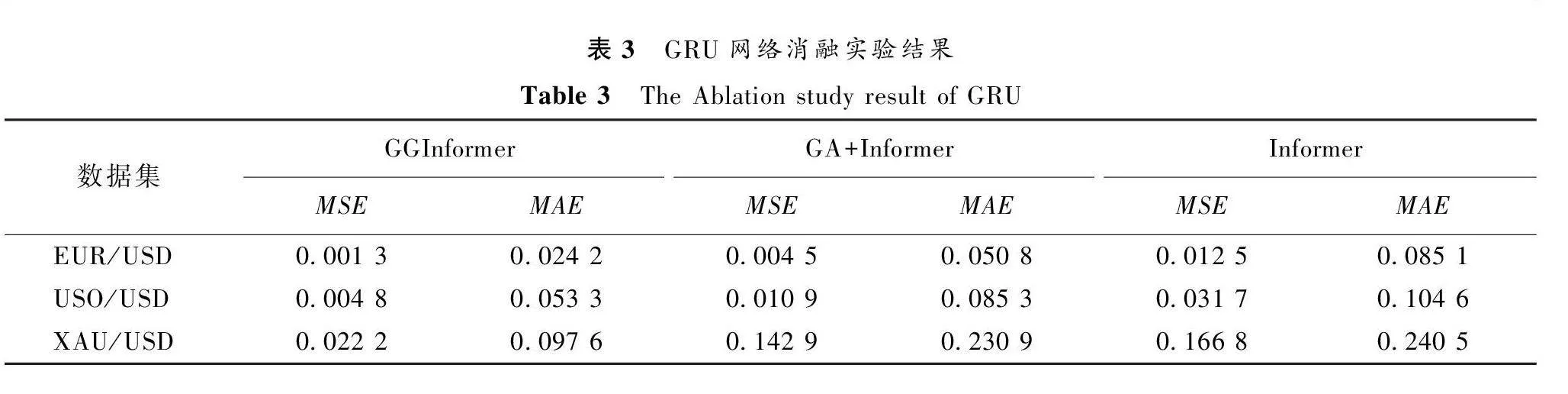
为了验证GRU网络对预测结果的影响，本文进行了相关消融实验研究，实验结果如表3所示，可视化结果如图4、图5和图6所示。

从消融实验结果可以看出，GRU网络对于GGInformer 模型的预测能力有明显提升，相比GA+Informe模型，GGInformer模型在EUR/USD数据集上的MSE结果降低了71%，在USO/USD数据集上的MSE结果降低了56%，在XAU/USD数据集上的MSE结果降低了84%。从图4、图5和图6中可以看出，虽然三种模型都可以大致拟合出预测数据的趋势曲线，但是GGInformer模型与其他两种模型相比，其预测结果与实际数据具有更好的拟合度，说明GRU网络可以进一步地提高模型对金融产品数据的预测能力。

3.4 长序列时序预测实验

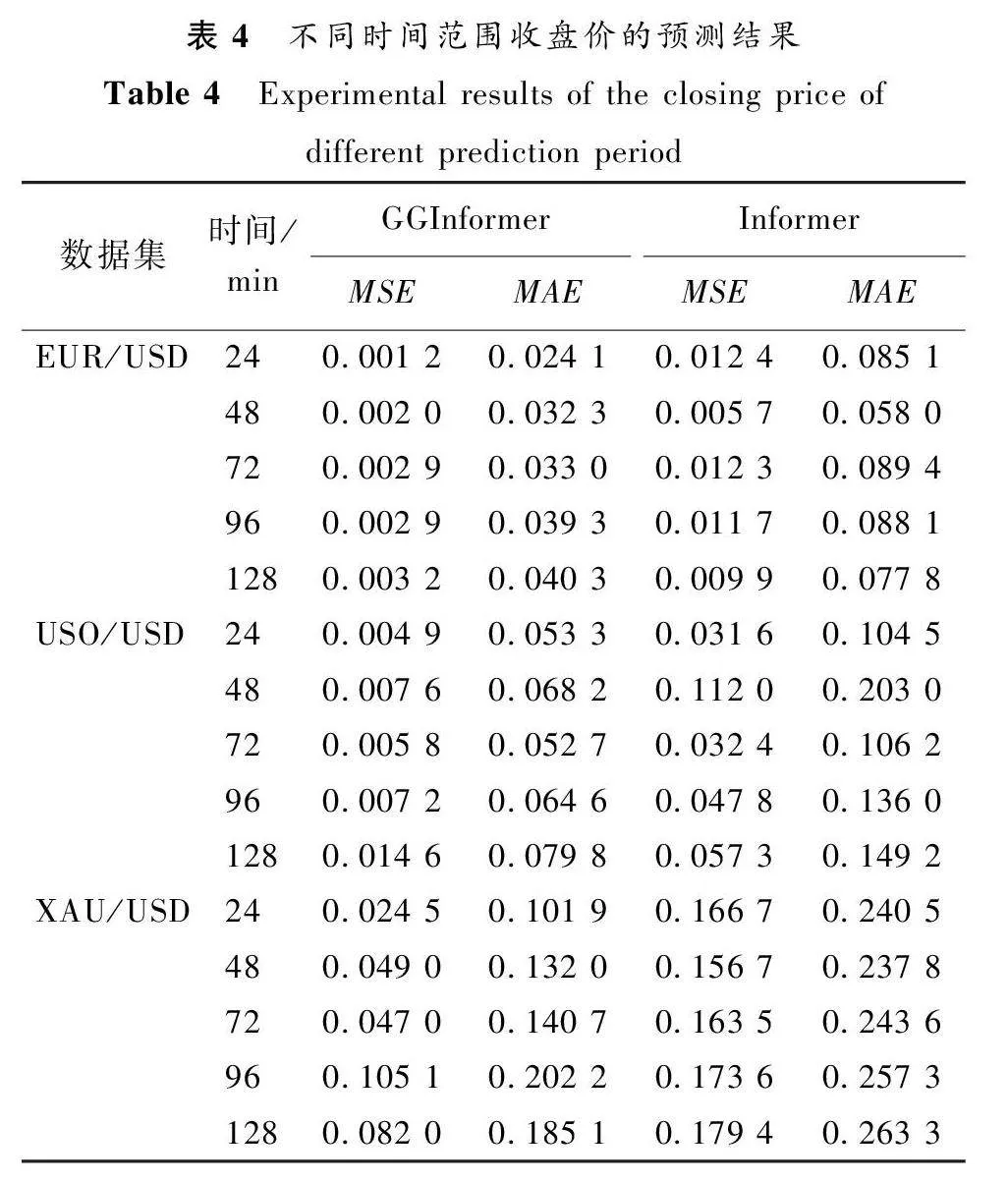
本文针对GGInformer模型的长序列时序预测能力进行了进一步的实验，选择Informer模型作为对比模型，分别预测24、48、72、96、128 min，预测结果如表4所示。

由表4可知，GGInformer模型在不同时间范围内收盘价的预测效果整体上优于Informer模型的预测效果，表明GGInformer模型在金融产品数据的长序列预测任务上同样有很好的效果。

4 结论

为了解决金融产品数据特征参数冗余，以及非线性的、长序列的金融产品价格预测难度大的问题，本文提出了用于预测金融产品交易价格的 GGInformer模型。将GGInformer模型在三种金融产品数据集上与四种基准预测方法进行了对比实验与消融实验，实验结果证明本文模型相对于其他预测模型在金融产品价格预测任务中更具有优势。此外，本文还通过长序列时序预测实验证明了模型解决长序列金融时序预测问题的能力。

参考文献：

［1］ ENGLE R F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation［J］. Econometrica， 1982， 50（4）： 987.

［2］ ARIYO A A， ADEWUMI A O， AYO C K. Stock price prediction using the ARIMA model［C］∥2014 UKSim-AMSS 16th International Conference on Computer Modelling and Simulation.Piscataway：IEEE Press，2015： 106-112.

［3］ RAMSEY M W， STEWART W R， JONES C J H. Real-time measurement of pulse wave velocity from arterial pressure waveforms［J］. Medical and biological engineering and computing， 1995， 33（5）： 636-642.

［4］ HUANG N E， SHEN S S. Hilbert-Huang transform and its applications［M］.Singapore： World Scientific Publish. 2014.

［5］ WU J A， CHEN Y， ZHOU T F， et al. An adaptive hybrid learning paradigm integrating CEEMD， ARIMA and SBL for crude oil price forecasting［J］. Energies， 2019， 12（7）： 1239.

［6］ 姚宏亮， 艾刘可， 王浩， 等. 均线滞后的时序自回归股市态势预测算法［J］. 郑州大学学报（理学版）， 2018， 50（3）： 60-66.

YAO H L， AI L K， WANG H， et al. Time series autoregressive stock market forecasting algorithm based on moving average hysteresis［J］. Journal of Zhengzhou university （natural science edition）， 2018， 50（3）： 60-66.

［7］ MEESAD P， RASEL R I. Predicting stock market price using support vector regression［C］∥2013 International Conference on Informatics， Electronics and Vision. Piscataway：IEEE Press，2013： 1-6.

［8］ NAIR B B， MOHANDAS V P， SAKTHIVEL N R. A decision tree-rough set hybrid system for stock market trend prediction［J］. International journal of computer applications， 2010， 6（9）： 1-6.

［9］ SELVIN S， VINAYAKUMAR R， GOPALAKRISHNAN E A， et al. Stock price prediction using LSTM， RNN and CNN-sliding window model［C］∥2017 International Conference on Advances in Computing， Communications and Informatics. Piscataway：IEEE Press，2017： 1643-1647.

［10］姜振宇， 黄雁勇， 李天瑞， 等. 基于时频融合卷积神经网络的股票指数预测［J］. 郑州大学学报（理学版）， 2022， 54（2）： 81-88.

JIANG Z Y， HUANG Y Y， LI T R， et al. Fusion of time-frequency-based convolutional neural network in financial time series forecasting［J］. Journal of Zhengzhou university （natural science edition）， 2022， 54（2）： 81-88.

［11］杨妥， 李万龙， 郑山红. 融合情感分析与SVM_LSTM模型的股票指数预测［J］. 软件导刊， 2020， 19（8）： 14-18.

YANG T， LI W L， ZHENG S H. Stock index prediction based on SVM_LSTM model with emotion analysis［J］. Software guide， 2020， 19（8）： 14-18.

［12］ZHANG Y A， YAN B B， AASMA M. A novel deep learning framework： prediction and analysis of financial time series using CEEMD and LSTM［J］. Expert systems with applications， 2020， 159： 113609.

［13］DING Q G， WU S F， SUN H， et al. Hierarchical multi-scale Gaussian transformer for stock movement prediction［EB/OL］.（2020-07-01）［2023-03-11］. https：∥www.ijcai.org/proceedings/2020/0640.pdf.

［14］HOLLAND J H. Adaptation in natural and artificial systems： an introductory analysis with applications to biology， control， and artificial intelligence［M］. Cambridge： MIT Press， 1992.

［15］LIU S S， ZHANG S， ZHANG X， et al. R-trans： RNN transformer network for Chinese machine reading comprehension［J］. IEEE access， 2019， 7： 27736-27745.

［16］ZHOU H Y， ZHANG S H， PENG J Q， et al. Informer： beyond efficient transformer for long sequence time-series forecasting［J］. Proceedings of the AAAI conference on artificial intelligence， 2021， 35（12）： 11106-11115.

［17］VASWANI A， SHAZEER N， PARMAR N， et al. Attention is all You need［C］∥Proceedings of the 31st International Conference on Neural Information Processing Systems. New York： ACM Press， 2017： 6000-6010.

［18］KITAEV N， KAISER ， LEVSKAYA A. Reformer： the efficient transformer［EB/OL］.（2020-01-13）［2023-03-12］. https：∥arxiv.org/abs/2001.04451.pdf.

［19］CHOROMANSKI K， LIKHOSHERSTOV V， DOHAN D， et al. Rethinking attention with performers［EB/OL］. （2020-09-30）［2023-03-12］. https：∥arxiv.org/abs/2009.14794.pdf.