基于多目标遗传算法的电梯维保路径规划方法研究

关键词：电梯;多目标优化;维保路径规划;优先级;多维保站点

中图分类号：TP18 文献标志码：A

0 引言（Introduction）

近年来，随着电梯数量的迅速增长，电梯维保人员短缺问题愈发严重，导致电梯安全运行和维保难题日益显现[1-2]。在当前的电梯维保路径规划工作中，维保站点的人员在接到任务后，需独立规划前往各台电梯的路线，而在不同电梯间转移的时间消耗较长，因此维保人员每日能完成的电梯维保数量并不理想。在长期工作中，维保人员工作负荷分布不均，时而空闲时而忙碌，这种情况会导致团队协作受阻、绩效下滑，进而影响整体工作效果[3]。除此之外，单个维保站点拥有的维保资源只能为有限范围内的电梯提供维保服务，为了对所有待维保的电梯做好服务，需要整合多个维保站点的资源。因此，开展各个待维保电梯之间的路径规划及保证各个维保站点之间的协同工作，具有重要意义。

本文首先剖析了电梯维保路径问题，并构建了一个多目标优化模型，旨在实现总维保成本最小化、维保人数最少化，以及员工工作时长标准差最小化。其次针对该模型提出了一种基于非支配排序遗传算法Ⅱ （Non-dominated Sorting GeneticAlgorithm Ⅱ，NSGA-Ⅱ）的电梯维保路径规划方案;在算法编码阶段采用双染色体编码，解决传统单染色体编码无法考虑任务优先级和维保任务归属站点的问题，并修改交叉和变异算子，以适应双染色体编码。最后将分解法[4]、全局法[5]和本文所提方案结合，使用Solomon标准测试数据集和实际案例进行对比验证，选出合适的方案为电梯维保路径规划提供有益参考。

1 研究现状（Research status）

目前，一部分学者围绕路径规划开展了大量的研究，HANNAN等[6]采用一种改进粒子群算法处理具有容量约束的垃圾回收路径问题;HUANG 等[7]使用蚁群优化算法解决无人机配送服务的车辆路径问题。学者对各类路径规划问题进行了研究，但鲜有针对电梯维保路径规划的研究。BLAKELEY等[8]通过解决周期性车辆调度问题（PeriodicVehicle Routing Problem， PVRP）创建高效的电梯维保日间路线，但仅考虑了周期性维保任务，而电梯的维保任务中不仅包含需要周期进行的预防性维护，还包括发生计划外故障的纠正性维护[9]。

电梯维保路径规划涉及的优化目标众多，电梯公司拥有的维保站点众多，每个维保站点的维保人员人数有限，各个维保任务对应的优先级也各不相同。因此，本文将电梯维保路径规划抽象为一个集合多优化目标（Multi-Objective VehicleRouting Problem， MOVRP）、多车场调度（Multi-Depot VehicleRouting Problem， MDVRP）及任务优先级（Vehicle RoutingProblem with Precedence Constraints VRP-PC）的车辆路径规划问题（vehicle routing problem， VRP）。针对上述VRP变体问题，现有研究中多采用启发式算法求解，例如粒子群算法（Particle Swarm Optimization，PSO）、模拟退火算法（SimulatedAnnealing Algorithm，SAA）、自适应大邻域搜索算法（AdaptiveLarge Neighborhood Search，ALNS）等，也有不少学者采用遗传算法进行求解[10-12]。

以上研究均取得较好的成果，但当前的研究往往将多目标优化、多车场调度及任务优先级等因素分别进行探讨。然而，在电梯维保路径规划中，这些因素需要综合考量，以实现更高效的规划方案。因此，本文以VRP为基础，综合考虑多目标优化、多车场调度、任务优先级3个因素，旨在解决电梯维保中存在的人员紧缺问题，均衡维保人员的工作时长，并降低公司维保成本。

2 问题描述和模型建立（Problem descriptionand model construction）

电梯涉及的维保任务众多，可以大体划分成3类维保任务：①电梯机械主要构件;②电梯电气部分的维护检修任务;③电梯的常规清洁。定期维护任务以第1类和第3类维保任务为主，而电梯电气部分的故障更具偶发性。以上3类维保任务的紧急程度各不相同，其中以电梯机械主要构件的维保任务最为重要，电气维保次之，常规性维保紧急程度最低。任务紧急程度越高，对应的维保时间越长，维保人员的工作负担也越重，因此在进行维保调度时，每一位维保人员只能负责一个紧急程度最高的维保任务。本文采用优先级表达任务的紧急程度，优先级数字越小，表示紧急程度越高。

2.1 问题描述

电梯维保路径规划问题可描述如下：一家维保公司拥有多个维保站点，当天要处理多个维保任务，但是每个维保站点的维保人员有限。不同的维保任务对应不同的服务时间和优先级;优先级数字小的任务，需要在优先级数字大的任务之前执行;每位维保人员的工作时长不能超过额定工作时长。维保人员从各自维保站点出发，依次为待维保电梯提供服务，在完成维保任务后，需返回原维保站点。

已知维保站点和维保任务的位置，维保任务的服务时间和优先级，以及维保人员的转场速度，在满足优先级和工作时长约束的前提下，求解使总维保成本最低，参与维保人数最少，以及每位维保人员工作时长差异程度最小的调度方案。

2.2 数学模型

为清楚地表述电梯维保路径规划的数学模型，本文定义了相关符号参数，具体如表1所示。

公式（3）和公式（4）表示维保人员k 的转场时间和任务维保时间;公式（5）表示维保人员k 的总工作时长，由转场时间和任务维保时间构成;公式（6）和公式（7）表示本文的优化目标，其中维保成本由路线成本和人员成本两个部分组成;公式（8）表示维保人员工作时间不超过额定工作时间;公式（9）和公式（10）表示进出平衡约束;公式（11）表示维保人员从维保站点出发，最后返回原先的维保站点;公式（12）表示单个维保站点参与维保的人员总数不超过其拥有的人员总数;公式（13）表示维保人员不能从一个维保站点到另一个维保站点;公式（14）表示每个维保任务只能由一位维保人员负责;公式（15）表示每位维保人员只能负责一个优先级为1的任务;公式（16）表示优先级约束。

3 算法构建（Algorithm construction）

在探讨电梯维保路径规划问题，尤其是当问题涉及多车场车辆路径问题（MDVRP）时，选择适当的求解方法至关重要。目前，针对MDVRP的两种主流处理方法——分解法和全局法各有优劣。为比较这两种方法哪种更为合适，需要深入分析它们的特点和适用场景。本文将NSGA-Ⅱ和上述两种方法结合，对公式（1）至公式（16）描述的多优化目标问题进行求解。以上两种方法考虑问题的角度不同，同一种编码和解码方式无法满足两种方案的需求，因此本研究为分解法和全局法设计了不同的编码和解码方式，并修改遗传算子以配合新的编码方式。为了方便决策者做出选择，引入模糊数学法在众多最优解中选取折衷最优解作为最终的调度方案。

3.1 双染色体编码、解码

各种VRP类型解决方案的标准编码是以一维整数数组的形式出现的，即单染色体编码，但其无法体现任务优先级和任务的归属站点，因此本研究采用双染色体编码，该编码方式可将任务优先级和任务归属站点信息直接体现在编码中。

3.1.1 全局法编码

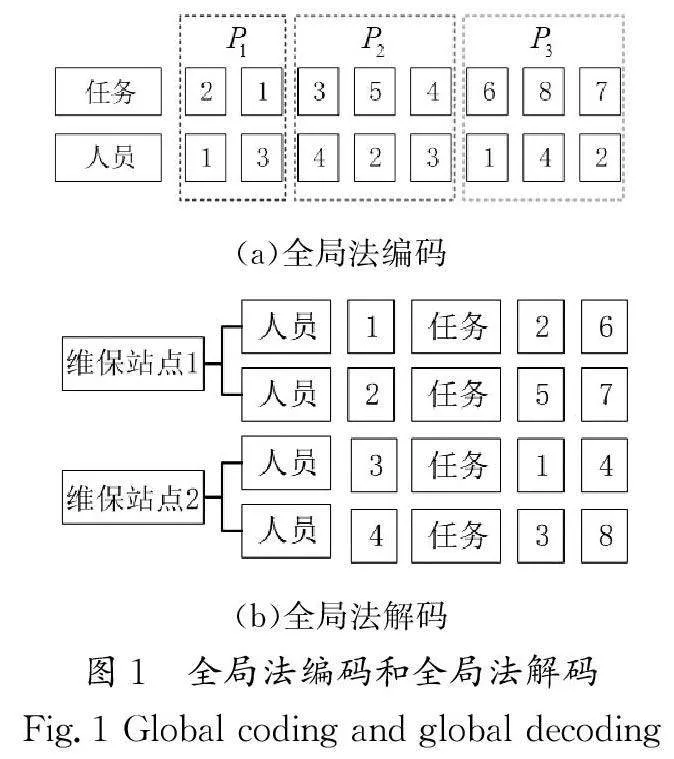
个体由2条染色体构成，第1条染色体表示维保任务编号，第2条染色体表示维保人员编号。假定1家维保公司拥有2个维保站点，当天需要处理8个维保任务，设置任务编号为1～8。每个站点有2位维保人员，1号站点的维保人员编号为1和2;2号站点的维保人员编号为3和4。将维保任务按优先级进行划分，每个优先级的任务集合为Pi，P1 对应任务编号为1和2;P2 对应任务编号为3、4、5;P3 对应任务编号为6、7、8。将任务按优先级数字从小到大次序分布在第1条染色体中，将维保人员编号分布在第2条染色体中，维保任务和维保人员编号一一对应，而维保人员编号又对应不同的维保站点，从而实现维保任务和维保站点的对应，全局法编码如图1（a）所示。

3.1.2 全局法解码

将不同维保人员对应的任务按其在染色体中出现的先后次序排列，从而得到每位维保人员的维保路径。将每位维保人员的编号和其归属的维保站点对应，最终得到每个维保站点的路径规划。双染色体编码不仅考虑了任务的归属站点信息，而且因其任务优先级排序与维保人员路径解码方向一致，确保了每位维保人员的路径满足优先级约束，从而有效地融合了任务优先级和任务归属站点的考量。采用全局法解码后的维保路径如图1（b）所示。

3.1.3 分解法编码

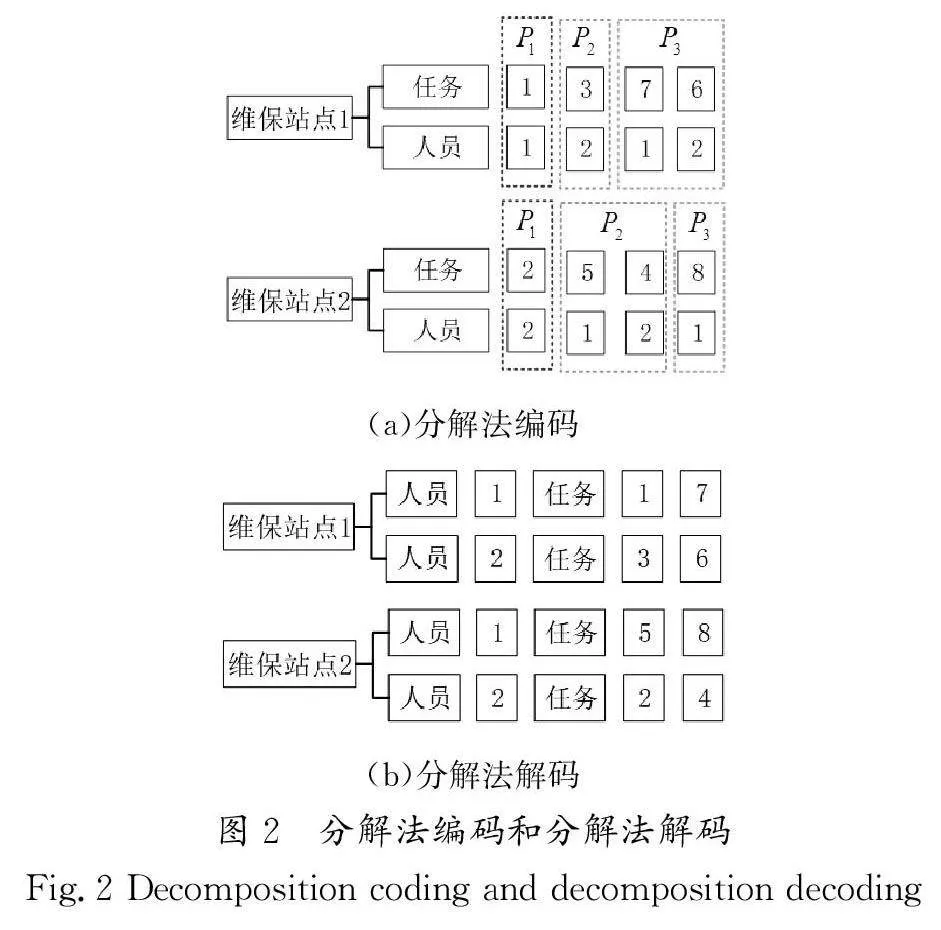
分解法在每次规划维保路径时，只需要考虑单个站点对应的任务，因此仅对单个维保站点内的维保人员进行编号即可，其余编码过程与全局法编码过程一致。假定1号维保站点负责1、3、6、7号任务;2号维保站点负责2、4、5、8号任务。分解法对应的分解编码图如图2（a）所示。

3.1.4 分解法解码

分解法单次只考虑一个维保站点，参与维保作业的维保人员都属于该站点，不需要考虑维保人员的归属站点划分问题。因此，将不同维保人员对应的任务按其在染色体中出现的先后次序排列，得到各维保站点的维保路径。采用分解法解码后的维保路径如图2（b）所示。

3.2 交叉算子和变异算子

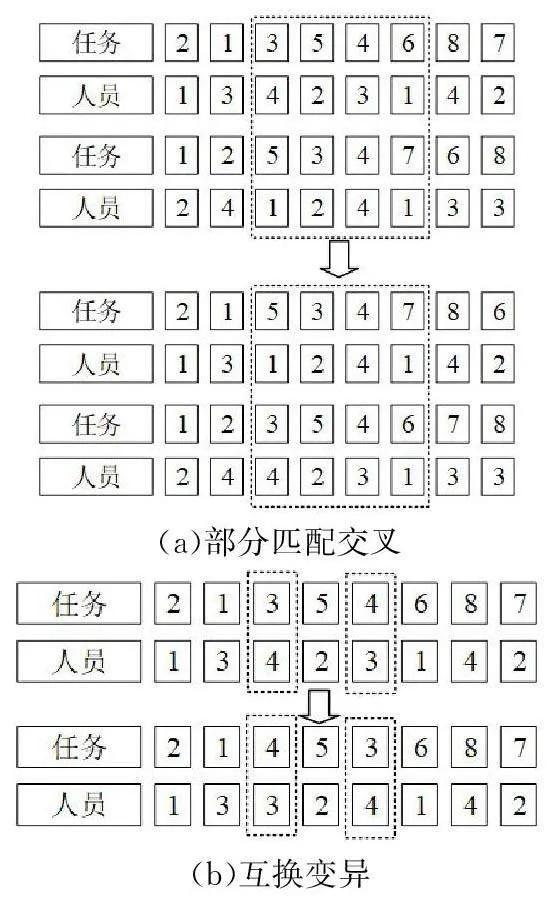
由于双染色体编码的染色体数量与传统编码不同，因此需要对为传统编码设计的遗传算子进行相应的调整。本文的交叉算子采用部分匹配交叉，该算子可以有效地避免基因重复及保留亲代的优秀特征。变异算子采用随机变异和互换变异两类。图3表示修改后的交叉、变异算子示意图。图3（a）表示部分匹配交叉，其适用范围包括任务和维保人员，执行交叉后为防止个别基因出现重复的情况，在交叉区域内建立每个染色体的匹配关系，在交叉区域外对重复基因应用此匹配关系以消除冲突;图3（b）表示互换变异算子，其适用于任务和维保人员，随机选中两对任务和对应的维保人员，置换选中的任务和维保人员的位置;图3（c）表示随机变异算子，其适用范围仅为维保人员，将选中的人员进行随机替换。

4 数值算例（Numerical example）

本文选取Solomon测试集中的C201、R201、RC201三种不同分布类型的算例，对提出的电梯维保路径规划模型和方案进行验证，由于Solomon测试集无法直接应用于电梯维保路径规划问题，因此对其做出如下修改。

以位置坐标点（30，60）、（40，20）及（75，50）为维保站点，在每个算例中设立16个优先级为1的维保任务，32个优先级为2的维保任务，52个优先级为3的维保任务。为了对比分解法和全局法在电梯维保路径规划中的效果，将NSGA-Ⅱ分别与分解法、全局法结合，组成2种不同的方案对不同算例进行求解。假定每位维保人员的调度费用为100元/位，单位出行费用为10元/千米，转场速度为70 km/h;算法一共进化1 000代;算法对应的交叉概率为0.7，变异概率为0.3。

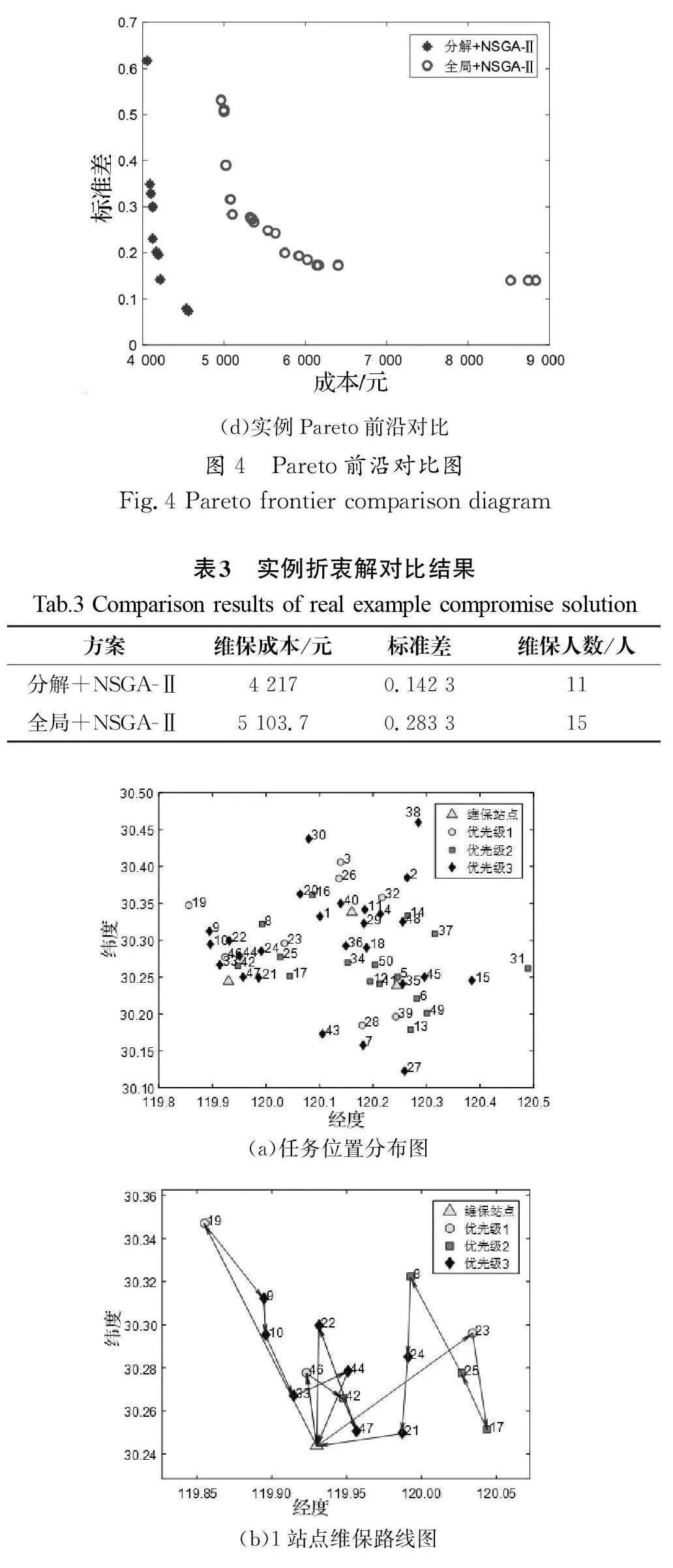
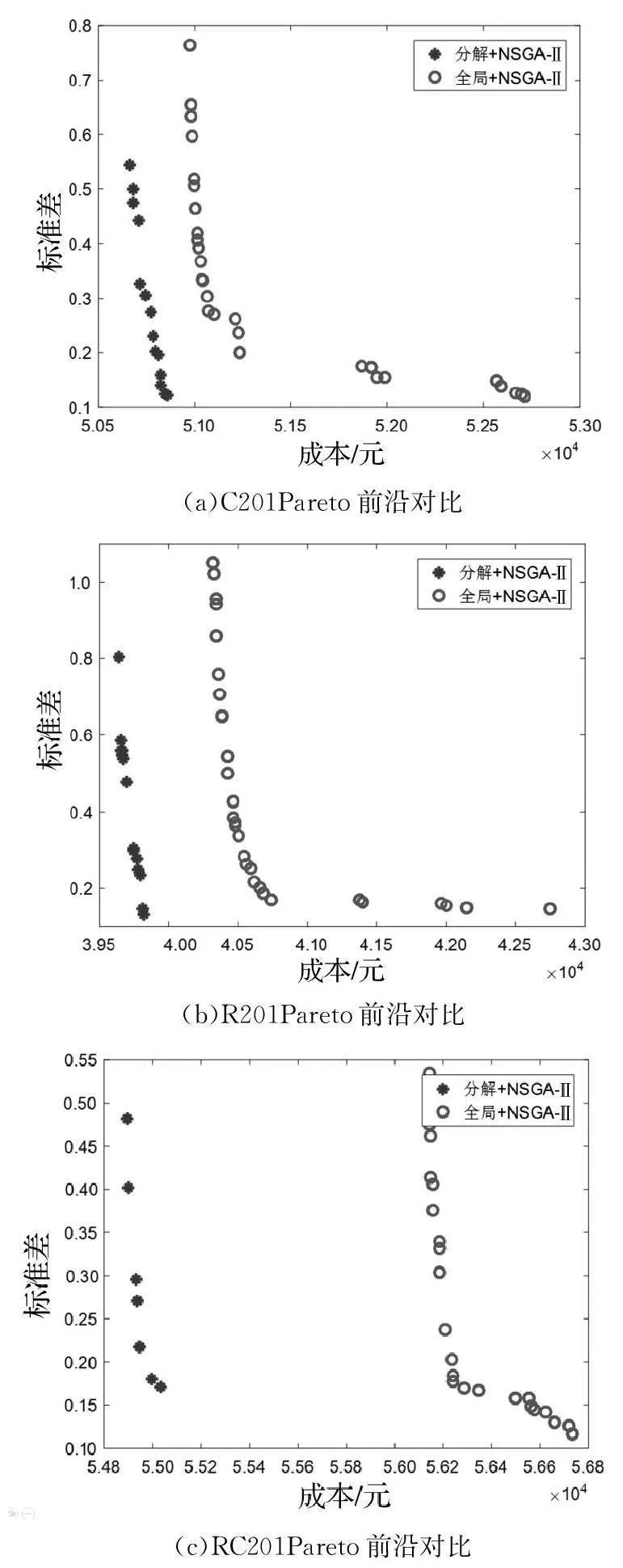
表2记录两种方案对应的折衷最优解，从中可知分解法和全局法在标准差的表现上相近，均能保障员工工作时长均衡，并且分解法在C201和R201算例上优于全局法;在总成本方面，分解法均优于全局法。通过折衷最优解无法直观地看出两种方案解集的优劣，为此绘制各方案的Pareto前沿对比图。

图4（a）至图4（c）表示分解法和全局法在C201、R201、RC201算例中的Pareto前沿对比图。由Pareto前沿对比图可知，分解法表现最优，说明在迭代次数相同的情况下，分解法更具优势。该结果与各方案在折衷最优解中的表现相吻合，证实了以折衷最优解作为决策者选择的可行性。

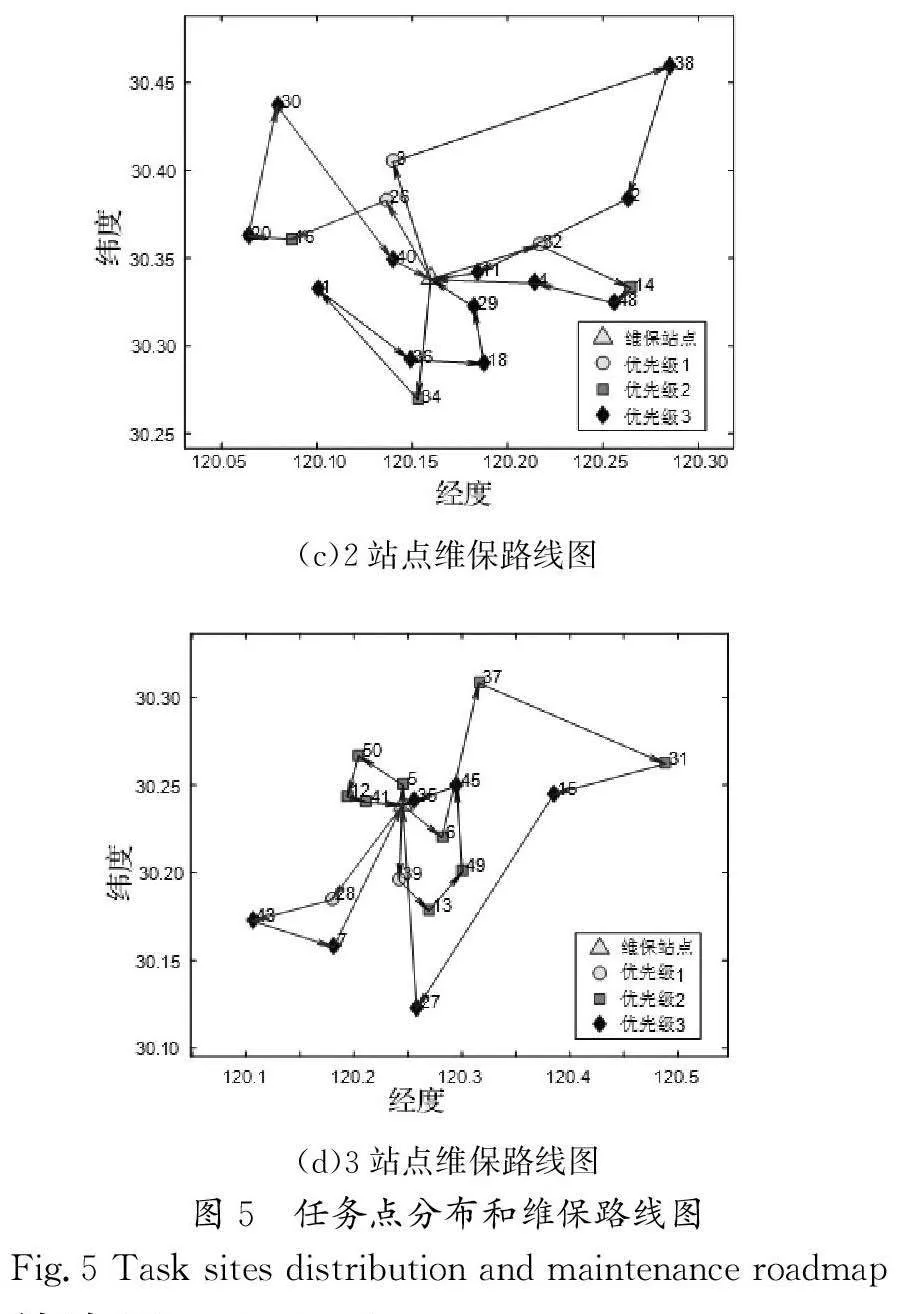
为验证算法的实际应用效果，选取某公司某时刻的维保任务，对提出的模型和方案进行验证。任务分布情况如图5（a）所示，一共有50个任务点，由3个维保站点完成;有3种任务优先级类型，分别为8个优先级为1的维保任务，16个优先级为2的维保任务，26个优先级为3的维保任务。在保留其他参数不变的情况下，由于各维保电梯之间距离较近，因此将转场速度修改为40 km/h。表3记录两种方案的折衷最优解在总成本、标准差和参与人数方面的表现;图4（d）记录两种方案对应的Pareto前沿。

分析表3可知，相较于全局法，分解法在成本上节约了17.3%，在员工工作时长标准差上减少49.7%，在人力资源上节约了26.6%;结合图4（d）所示的Pareto前沿对比图可知，分解法结合NSGA-Ⅱ方案得到的解更优秀，说明在迭代次数相同的情况下，采用分解法更适用于电梯维保路径规划问题。

图5（b）至图5（d）表示3个维保站点的维保路径图，维保人员从维保站点出发，首先对优先级为1的任务提供服务，其次对优先级为2和3的任务提供服务，并且每条路径中只存在一个优先级为1的任务，满足优先级约束条件。上述结果表明，本文所提方案可为电梯维保路径规划提供有益参考。

5 结论（Conclusion）

本文研究电梯维保路径规划任务，以总维修成本最低、维保人数最少及均衡员工工作负载为优化目标，求解电梯维保路径规划问题。首先，建立多目标优化模型，并考虑任务优先级和多维保站的调度问题，其次，利用NSGA-Ⅱ对构建的多目标优化模型进行求解，最后，通过Solomon算例和实例得到以下结论。

（1）双染色体编码解决了单染色体编码未考虑任务优先级和维保任务归属站点的问题，可以应用于电梯维保路线调度问题。

（2）应用NSGA-Ⅱ算法，实现了多维保站点的维保路径规划，通过Solomon测试集和实例验证发现，在迭代次数相同的基础上，分解法优于全局法。在实例上的表现如下：采用分解法在成本上节约了17.3%，在员工工作时长标准差上减少了49.7%，在人力资源上节约了26.6%。因此，针对电梯维保路线调度问题，采用分解法更合适。

本文所提方法为电梯维保路径规划提供了一种可行的调度办法。

作者简介：

魏义敏（1986-），男，博士，副教授。研究领域：弹性波，故障诊断，路径规划。

丰炜（1996-），男，硕士生。研究领域：电梯维保路径规划。