基于时间信息增强Transformer的短时交通流预测模型

关键词：交通流预测;深度学习;长短期记忆网络;Transformer;图卷积网络

中图分类号：TP399 文献标志码：A

0 引言（Introduction）

随着我国城市交通拥堵问题愈发严重，建设智能交通系统已成为提高路网通行效率，缓解交通拥堵问题的重要手段[1]。实时、准确的交通流预测不仅能为交通信号控制提供必要的信息支撑，还能辅助规划最优出行路线以充分利用路网的承载能力，是智能交通系统的重要组成部分。

近年来，基于深度学习的交通流预测方法表现出了十分优秀的性能[2]。卷积神经网络（Convolutional Neural Network，CNN）、图卷积网络（Graph Convolutional Network，GCN）和循环神经网络（Recurrent Neural Network，RNN）已被广泛应用于交通流预测领域[3-5]。

然而，现有深度学习方法在提取多维空间特征、同时建模短期和长期时间依赖关系方面存在一定的局限性，并且多数研究人员仅使用预测精度作为模型的评价指标，忽略了模型复杂度对模型实时响应能力的影响。针对上述问题，本文提出了一种基于时间信息增强Transformer的短时交通流预测模型（TIE-Trans），在进一步提高对时空特征提取能力的同时，有效地抑制了模型复杂度的增长。

1 相关工作（Related work）

以往的交通流预测方法大致可分为参数方法、机器学习方法和深度学习方法3类。其中，参数方法和机器学习方法的提出时间较早，现有的研究一般将其与深度学习方法结合使用。

例如，MA等[6]利用K均值算法对包含不同交通流量模式的数据进行分组，再利用深度学习方法对每组数据分别建立预测模型，避免了包含不同交通流量模式的数据之间相互干扰。游茜[7]同时使用稀疏自动编码器和LSTM 捕获交通流数据中的时间相关性，并使用注意力机制进一步改善预测模型的性能。

近年来，深度学习方法是交通流预测领域的重点研究内容。LI等[8]提出了一种基于小波分解、CNN和LSTM（Longshort-term memory network， LSTM）的模型用于高速公路流量预测。为了提高长时预测的精度，该模型首先利用小波分解将原始交通流数据分解为高频数据和低频数据，再分别使用CNN-LSTM模块捕获时空特征。ZHENG等[9]设计了一个包含注意力机制的conv-LSTM 模型以增强捕获时间特征的能力。该模型还使用了多组深度神经网络分别捕获近期数据、日周期数据和周周期数据的时空特征，有效地提高了预测精度。YAN等[10]重新设计了Transformer模型中编码器、解码器的结构以捕获全局和局部的空间相关性，解决了原始Transformer模型无法直接处理邻接矩阵的问题。GUO等[11]将动态GCN模块嵌入至Transformer模型内部，以动态方式对空间相关性进行建模。该模型还对Transformer中的多头自注意力机制进行了优化，解决了传统多头自注意力在数值数据预测中局部趋势不可知的问题。CHEN等[12]同时使用预测解码器和回忆解码器构建了一个双向Transformer模型，利用回忆解码器执行“现在-过去”的学习任务，为预测任务提供辅助信息。

3 模型结构（Model structure）

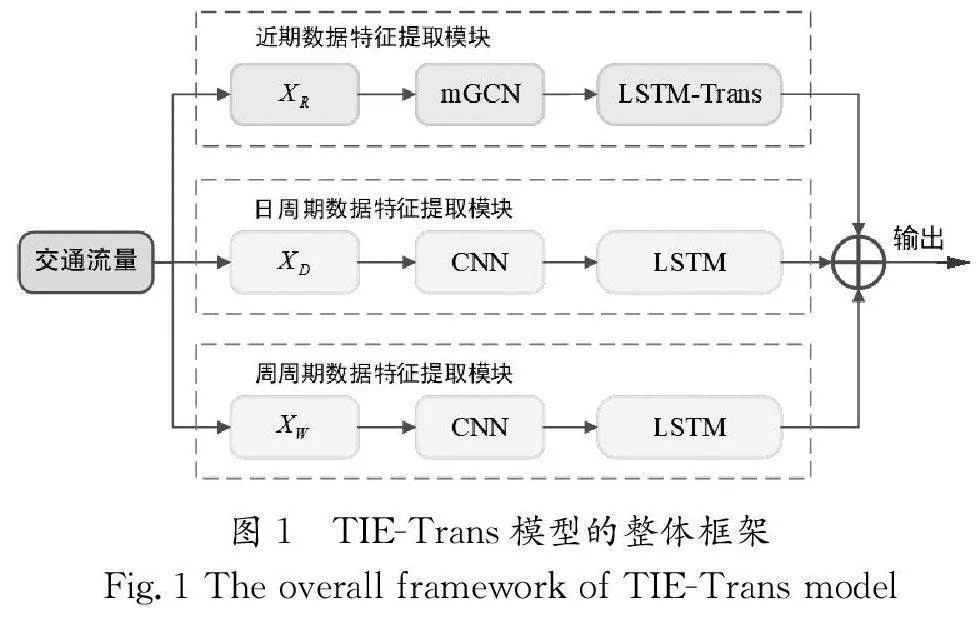
为了更有效地建模交通流量中的时空特征和周期性特征，本文提出了一种基于时间信息增强Transformer的短时交通流预测模型（TIE-Trans），其整体框架如图1所示。在TIETrans模型中，输入的流量数据会被预先分为“近期数据”“日周期数据”“周周期数据”3组。与此相对应的是，模型也包含一个近期数据特征提取模块和两个周期性数据特征提取模块。近期数据特征提取模块由一个多图卷积层和一个LSTMTrans层组成，能够有效地建模多个维度的空间相关性和不同距离上的时间依赖关系。周期性数据特征提取模块由CNN和LSTM网络组成，它不仅能够捕获交通流量的周期性变化规律，用于修正由近期数据得到的预测值，还具有较低的时间复杂度，保证预测模型的响应速度。使用3个可训练的权重矩阵将上述3个模块的输出进行加权融合，即可得到最终的预测结果。

3.1 近期数据特征提取模块

3.1.1 多图卷积层

由于以RNN为代表的时序预测模型无法有效地捕获节点间的空间依赖关系，因此需要使用CNN、GCN等神经网络与时序预测模型联合提取时空特征。然而，CNN最初是一种用于处理图像数据的神经网络，只能处理规则的欧式数据，如图2（a）所示。与CNN相比，GCN可以通过邻接矩阵表示不规则的路网空间结构，如图2（b）所示，在交通流预测任务中更具优势。值得注意的是，原始的GCN通常是基于拓扑图或距离图来构建邻接矩阵，这种单一的图结构很难充分描述不同交通节点间的空间依赖关系[13]。为了捕获更深层次的空间依赖关系，本研究设计了一个流量相似性图，并与距离图一同组成多图卷积网络。

3.2 周期性数据特征提取模块

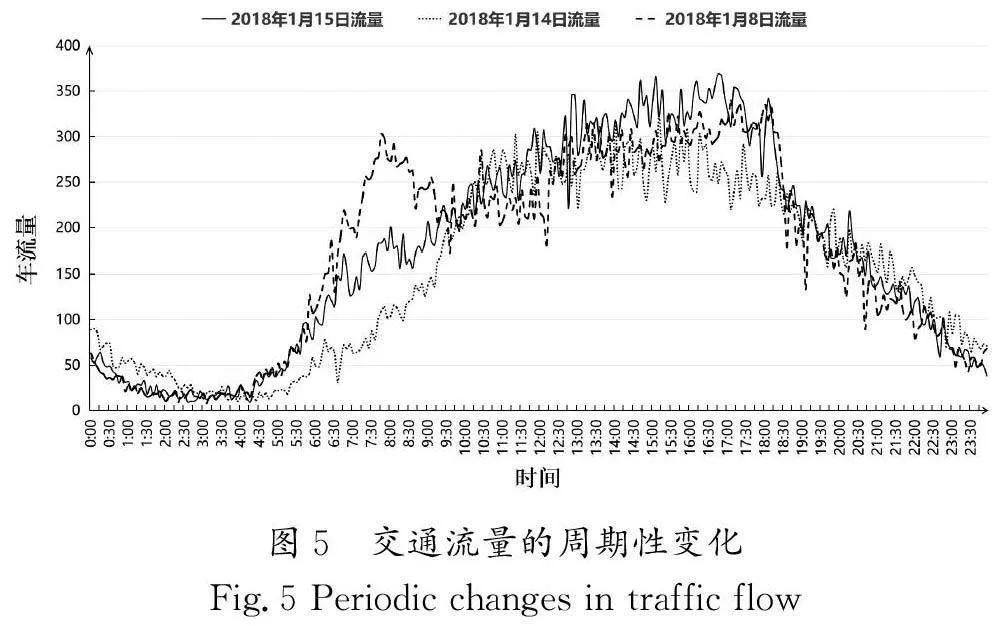
通常情况下，人类活动具有一定的规律性，这使得每日或每周的交通流量模式会呈现出明显的周期性变化，如图5所示，交通流量具有“日周期”和“周周期”变化规律[15]。然而，交通流预测模型输入数据的时间跨度一般不会超过2 h，这远远小于“日周期”和“周周期”的周期长度。如果直接将过去一周的交通流量数据一次性输入预测模型中，不仅会使得模型的计算复杂度急剧增大，还会引入大量的无关数据，进而对预测结果产生负面影响。

为了捕获交通流量的周期性变化，一些研究人员将其设计的预测模型复制为3份，分别建模“近期数据”“日周期数据”“周周期数据”的时空相关性。为了提高预测模型的响应速度，本研究采用了一种更加轻量化的模型结构。CNN是交通流预测领域中常用的神经网络之一，它使用一个固定形状的卷积核以聚合不同交通节点间的空间信息。与多图卷积网络相比，CNN不需要实时计算流量相似性矩阵，时间复杂度明显降低。因此，本研究使用两层CNN和两层LSTM 提取周期性数据的时空特征，并使用3个可训练的权重矩阵融合3个模块的输出结果。实验结果显示，相较于使用3个GCN-LSTM-Trans模块，本文采用的轻量化模型的训练时间仅为前者的37%，有效地抑制了模型复杂度的增长。

4 仿真实验（Simulation experiment）

4.1 数据集

为了评估本模型的真实性能，研究人员在PEMS04（Performance Measurement System Dataset 04）和PEMS08（Performance Measurement System Dataset 08）两个公开数据集上进行了实验。数据集由加利福尼亚州交通运输部提供，主要包含高速路网中的车流量、行驶速度、车道占用率等信息，数据的细粒度为5 min。其中，PEMS04数据集包含307个监测点的交通数据，数据的时间跨度为2018年1月1日至2018年2月28日。PEMS08数据集包含170个监测点的交通数据，数据的时间跨度为2016年7月1日至2016年8月31日。本研究使用历史1 h的车流量数据预测未来1 h（细粒度为5 min时，共12步）的车流量数据。

4.2 基线模型

本研究选取了6个预测模型作为本工作中的基线模型，包括1个参数模型、2个基础的深度学习模型及3个最新的深度学习模型。下文将对这些模型进行简要介绍并注明模型来源。

（1）ARIMA[16]：ARIMA模型是自回归模型（AR）、微分过程（I）和移动平均模型（MA）的组合。ARIMA模型可以捕捉数据的变化趋势，但很难捕捉非线性关系。

（2）LSTM[17]：LSTM是RNN的一个改进版本，它通过引入门控机制缓解RNN难以捕获长期时间依赖关系的问题。

（3）CNN-LSTM[18]：CNN是机器视觉领域中常用的模型之一，也可以用于聚合不同交通节点的空间信息。在此模型中，它与LSTM串行连接以联合提取时空特征。

（4）ttnet[10]：ttnet是Transformer模型迁移到交通流预测领域后的版本，它对原始模型中的嵌入层和编码-解码器部分进行了优化。

（5）ASTGNN[11]：ASTGNN是Transformer的一个改进版本，它将动态图卷积网络嵌入Transformer模型的内部以捕获时变的空间依赖关系。

（6）BI-STAT[12]：BI-STAT是一种双向Transformer网络，它利用回忆解码器增强了模型捕获上、下文信息的能力，并利用动态停止模块降低了模型的计算复杂度。

4.3 实验设置

本研究首先按照6∶2∶2的比例将所有数据划分为训练集、验证集和测试集。之后，对所有的输入数据进行0均值归一化，并将其输入预测模型中进行训练。在训练过程中，模型会基于均方误差（MSE）更新内部参数。在测试阶段，使用平均绝对误差（MAE）、均方根误差（RMSE）及平均绝对百分比误差（MAPE）评估模型的预测精度。此外，本研究会记录模型每轮次的训练时长，以评估模型的时间复杂度。

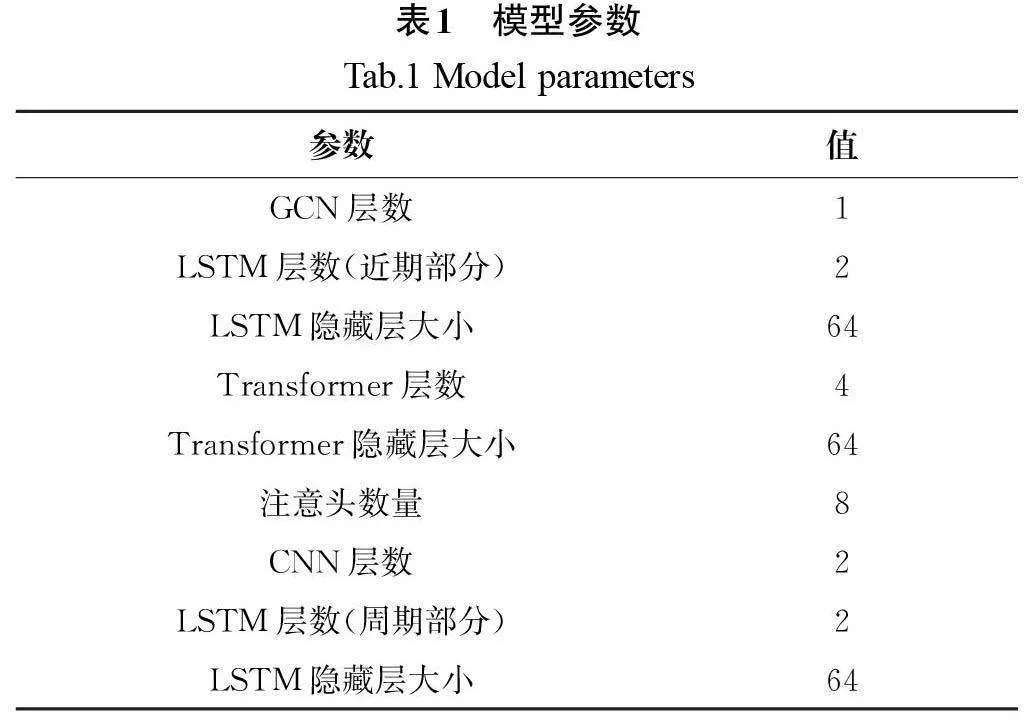
本模型基于Pytorch 深度学习框架构建，并在一张RTX 3060上进行训练。模型总计训练80轮，每轮训练后会立即进行一轮验证以记录模型性能。训练结束后，本研究再将验证过程中记录的最佳的参数加载至模型中进行测试。在训练过程中，将dropout设置为0.1，初始学习率设置为0.001，并且当预测精度连续5轮没有提升时，学习率会降低50%。具体的模型参数设置如表1所示。

4.4 实验结果及对比分析

将本模型与6个基线模型在PEMS08和PEMS04两个数据集上进行对比，对比内容为未来15 min、30 min和60 min的预测精度，未来60 min内的平均预测精度，以及模型的时间复杂度。表2至表4中，性能最佳的数据用加粗字体和下划线标记，性能次佳的数据用加粗字体标记。

首先，TIE-Trans在不同数据集、不同预测时间步长上的RMSE指标均优于所有基线模型的RMSE指标。对于MAE和MAPE指标，TIE-Trans也与最新的基线模型处于同一性能水平。其次，相较于基线模型，TIE-Trans在PEMS04数据集上的性能提升幅度略高于在PEMS08数据集上的性能提升幅度。这表明本文模型在更大的区域内捕获更加复杂的时空相关性时，也具有良好的表现。此外，如表4所示，TIE-Trans在时间复杂度上的表现远胜于3个最新的基线模型的表现。与ttnet和ASTGNN 相比，TIE-Trans在预测精度上提高了约5%的同时，时间复杂度分别降低了18%和65%。与最优的基线模型BI-STAT相比，TIE-Trans在预测精度上提高了约1%的同时，时间复杂度降低了87%。

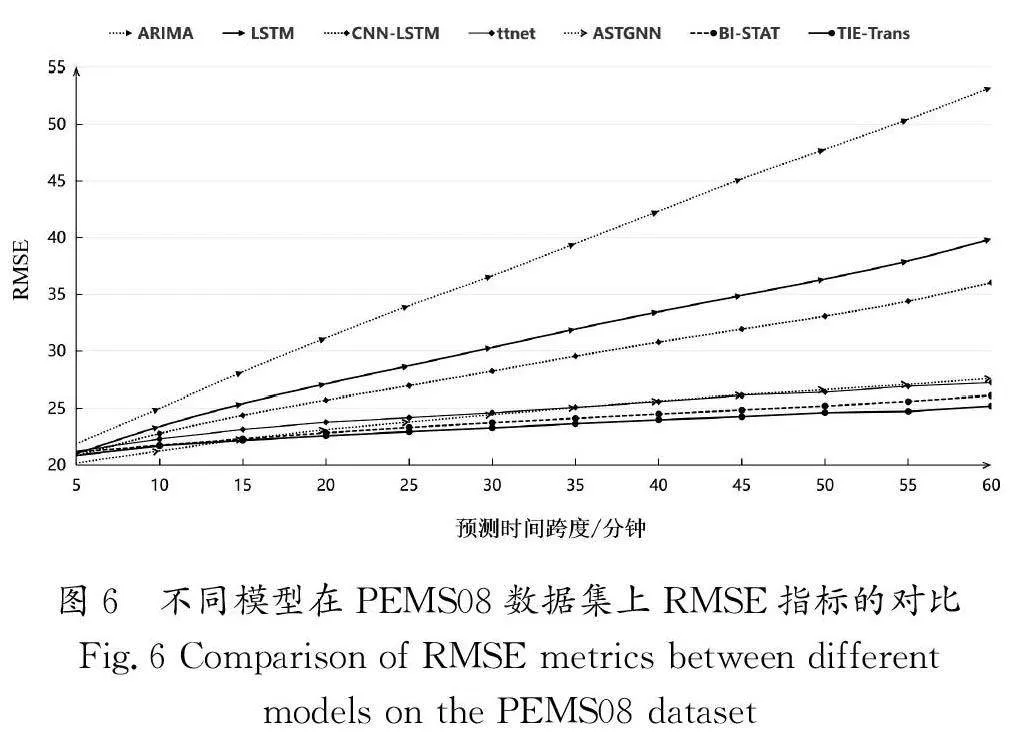
为了更直观地展示预测模型在不同预测时间步长上的性能，本研究在图6中对比了所有预测模型的误差变化趋势。从图6中可以看出，在预测时间步长较短时，各种深度学习模型的性能与ARIMA模型的性能差距不大，但随着预测时间的不断增加，ARIMA模型的误差急剧提高。在深度学习模型中，CNN-LSTM模型的预测精度明显高于LSTM 模型的预测精度，这表明引入空间信息对时间序列预测有着十分积极的影响。在中长期预测方面，TIE-Trans的预测误差低于所有基线模型的预测误差，并且误差并未随着预测时间的延长而明显增加。这是因为模型利用了交通流量的周期性变化规律对预测结果进行了进一步的修正。

5 结论（Conclusion）

本文提出了一种带有短期时间信息增强的Transformer模型，用于解决传统深度学习方法无法同时建模短期和长期时间相关性的问题。同时，基于距离图和流量相似性图构建了一个多图卷积网络，提高了模型建模远距离空间相关性的能力。针对捕获交通流的周期性特征可能导致模型复杂度急剧增大的问题，本文设计了一种轻量化的模型结构提取、融合周期性特征，保证了预测模型的实时响应能力。在两个真实数据集上的仿真测试结果显示，本文所提预测模型在预测精度和响应速度上的综合表现均优于基线模型的综合表现。这表明所设计的多图卷积网络与LSTM-Trans网络在提取时空特征方面具有优秀的性能。需要注意的是，在融合交通流的周期性特征方面，本研究使用了3个固定的权重矩阵融合近期、日周期和周周期数据的预测结果。未来的研究，将考虑实时计算近期流量数据与周期性流量数据之间的时空相关性，并据此对权重矩阵进行动态调整以进一步提高预测精度。

作者简介：

张鸣剑（1998-），男，硕士生。研究领域：交通流量预测。

叶宝林（1984-），男，博士，副教授。研究领域：智能交通。

董睿（1985-），男，硕士，讲师。研究领域：智能控制，嵌入式系统。

陈滨（1987-），男，博士，副教授。研究领域：智慧交通，图像处理，深度学习。