基于复杂特征的心动周期检测算法

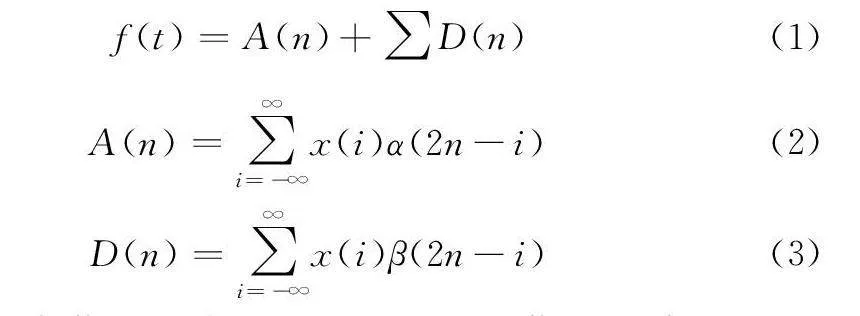
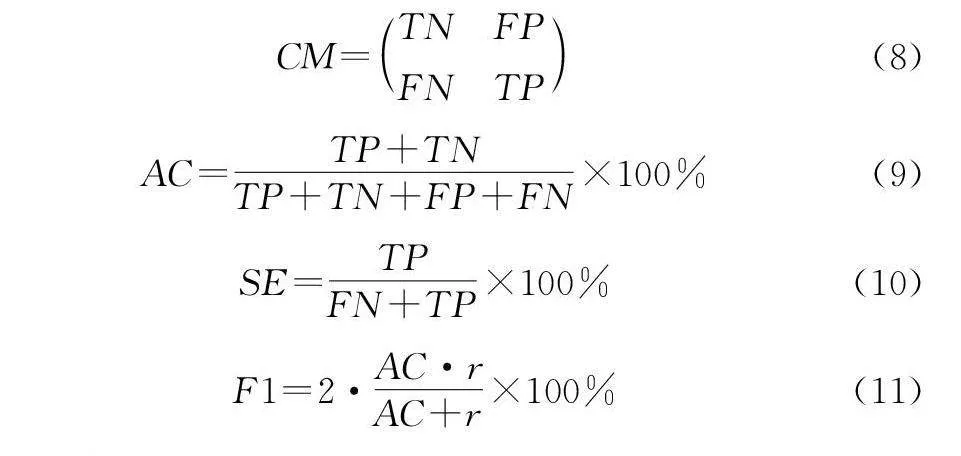
关键词：心冲击信号;Shapelet;小波变换;人工神经网络

中图分类号：TP389.1 文献标志码：A

0 引言（Introduction）

随着健康意识的提升和医疗技术的不断进步，人们开始更加关注自身的心血管健康状况。因此，心率和心动周期作为评估心血管系统健康状况的关键指标，受到了广泛关注。传统心率检测方法的采集设备需要将传感器电极直接与人体相连接，这种方式可能会给患者的日常生活带来不适和不便。心冲信号是一种非侵入性的生理信号，其优势在于采集设备不需要与人体直接接触。这一特点使得BCG能够实现长期的、家庭式的无接触健康监测，进而有效地预测和评估心血管疾病的风险[1]。

近年来，基于BCG信号进行无接触的心动周期检测已经得到了广泛的研究。ALVARADO-SERRANO等[2]首先检测BCG信号的前4个心跳来定义初始参数，其次学习这些参数来识别下一个心跳。HAI等[3]将BCG信号片段表述为图像，馈送到门控循环单元（GRU）网络中进行特征提取，从而实现心动周期检测。王炬等[4]根据BCG波形中的极大值点截取BCG子序列进行模板匹配。上述算法对模板波形的质量要求较高，一旦出现模板错误，将会在很大程度上降低后续心动周期检测的精度。为了提高心动周期检测的精度，完善无接触健康监测技术，本文提取了BCG信号的Shapelet特征和小波特征，与传统的时域特征相比，Shapelet更具有鲁棒性，而小波特征则可以反映信号的各种细节。将两种特征相融合，命名为Shapelet-WT特征，通过该复杂特征完善心动周期的识别检测。

1 特征提取（Feature extraction）

1.1 信号的采集与预处理

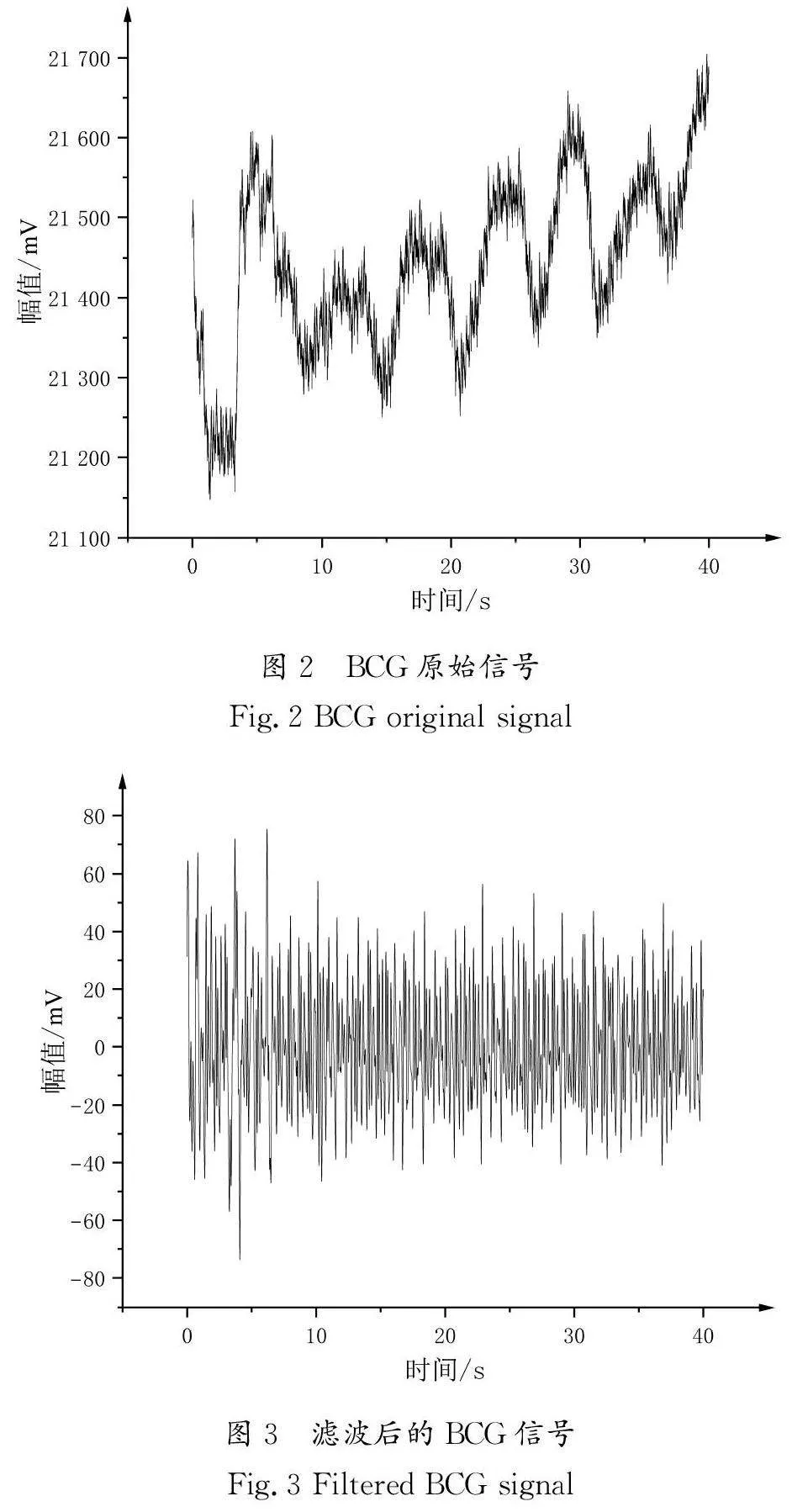
本实验使用基于微弯曲光纤维传感器的BCG信号采集坐垫采集BCG信号（采样率为500 Hz），它利用微弯管的形变促使接收器收到的光强发生改变，基于这种方法制作的传感器灵敏度高、成本低、传输的信号比较稳定[5]。基于微弯曲光纤维传感器的BCG信号采集坐垫如图1所示。同步采集ECG信号（采样率为500 Hz），采集的每段信号数据均含有时间戳，这种方式解决了两种不同信号同步难的问题。BCG信号在采集过程中极易受到外界噪声（呼吸、体动、电路自身噪声等干扰信号）的干扰，从而影响后续算法检测的精度，为了突出BCG信号中的有效信息，需要对BCG信号进行预处理，降低噪声的影响。本研究使用了截止频率为0.4～10 Hz的二阶巴特沃斯带通滤波器滤除BCG信号中包含的呼吸信号和高频噪声。BCG原始信号如图2所示，经过带通滤波器滤波后的BCG信号如图3所示。

1.2 小波变换提取特征

小波变换[6]（Wavelet Transform，WT）是一种新的变换分析技术，它针对短时傅里叶变换局部化的思路做了改良和继承，同时解决了窗口大小不随时间改变而改变等缺陷，能够提供一个随频率改变的时频窗口，是进行信号时频分析和处理的理想工具。本文利用小波变换把BCG信号在不同频率中的特征提取出来，对信号进行频带分析，将最后一级的近似信号和每一级的细节信号作为模型训练所需的特征。BCG信号f（t）的二进小波分解可表示如下：

其中：A 是近似信号，为低频成分;D 是细节信号，为高频成分;x（i）代表第i 个节点的BCG信号，低频和高频成分分别由α近似系数及β 细节系数构成。上述过程迭代地应用于每个级别的低频成分，直到达到指定级别。多尺度分解的信号频带分布如图4所示，研究人员选择第五层的近似信号和各层的细节信号作为特征构建特征向量。

1.3Shapelet特征提取

Shapelet[7]算法是一种时间序列分析工具，它的准确性和可解释性使其在时域分析领域备受瞩目。Shapelet作为时间序列的子序列，是该序列中最具特色的部分，将其作为特征能够有效地区分两类时间序列的差异。使用时间序列到Shapelet的距离作为特征的分类算法，大幅提高了分类识别的灵敏度，并增强了算法的可解释性。

研究人员提取了BCG信号中10种不同长度的Shapelet，在清除冗余和相关性不高的Shapelet后，得到了精简后的Shapelet共43个，不同长度的Shapelet如图5所示。精简后的Shapelet解决了其形式的局限性，同时保持了多样性，降低了算法的复杂度和缩短了学习时间。通过Shapelet变换[8]将Shapelet与BCG子序列之间的距离作为特征值，将BCG子序列变换到基于Shapelet的特征空间中，目的是缩减子序列的长度，但同时也保留了子序列中包含检测心动周期的关键信息，图6为某BCG子序列和其映射到同一空间的Shapelet，两个时间序列的最佳匹配距离即所需要的特征值。

2 ANN网络模型的搭建（Construction of ANN ）

2.1 网络结构

人工神经网络（ANN）[9]是在生物学的基础上，将大脑对外界刺激的反应进行理解和抽象，模仿大脑神经网络结构和功能而建立的数学模型。该模型同时具备并行处理和分布式处理能力，并且结构简单，网络参数多，计算量大，能够承受多隐层网络的规模。

本文使用的ANN具有5层结构，如图7所示。第一层是输入层，第二层、第三层、第四层是隐藏层，第五层是输出层。输入层接收小波变换和Shapelet算法提取的特征数据。隐藏层是神经网络中的内部处理层，这些神经元在网络内部形成一个中间层，多个隐藏层能够在各个层次上对输入特征进行多级抽象，从而更有效地对不同数据进行线性划分。本研究设置了3个隐藏层防止隐藏层过多导致的过拟合和训练困难问题。Dropout层[10]放在隐藏层中用于解决模型的过拟合问题。

2.2 激活函数和损失函数的选择

在训练神经网络时，超参数的调整是必不可少的。深度学习神经网络中常用的超参数有梯度下降优化器、损失函数和激活函数。激活函数经常用于解决非线性问题，它可以帮助神经网络学习复杂的数据模型。Sigmoid、Tanh和ReLu是常用的激活函数。Sigmoid函数和Tanh函数可能会遇到梯度消失的问题，而ReLu[11]函数的输出范围从0到无穷大，解决了梯度消失的问题，并且其收敛速度比Sigmoid函数和Tanh函数的收敛速度更快。所以，研究人员在隐藏层使用ReLu函数，在输出层使用Sigmoid函数。

2.3 优化器和学习率

优化器是在深度学习反向传播过程中，计算网络的权重和偏差导数，以完成网络参数的更新，指导损失函数能够以适当的幅度朝着正确的方向更新，使得损失函数值不断逼近全局最小。本文使用的优化器Adam是一种随机优化算法，与传统随机梯度下降算法不同的是，它更善于处理稀疏梯度和非平稳目标，初始化学习率并且根据训练数据迭代及时更新神经网络权重，通过自适应地调整学习率改进梯度下降问题。

2.4 隐藏层神经元的数量设置

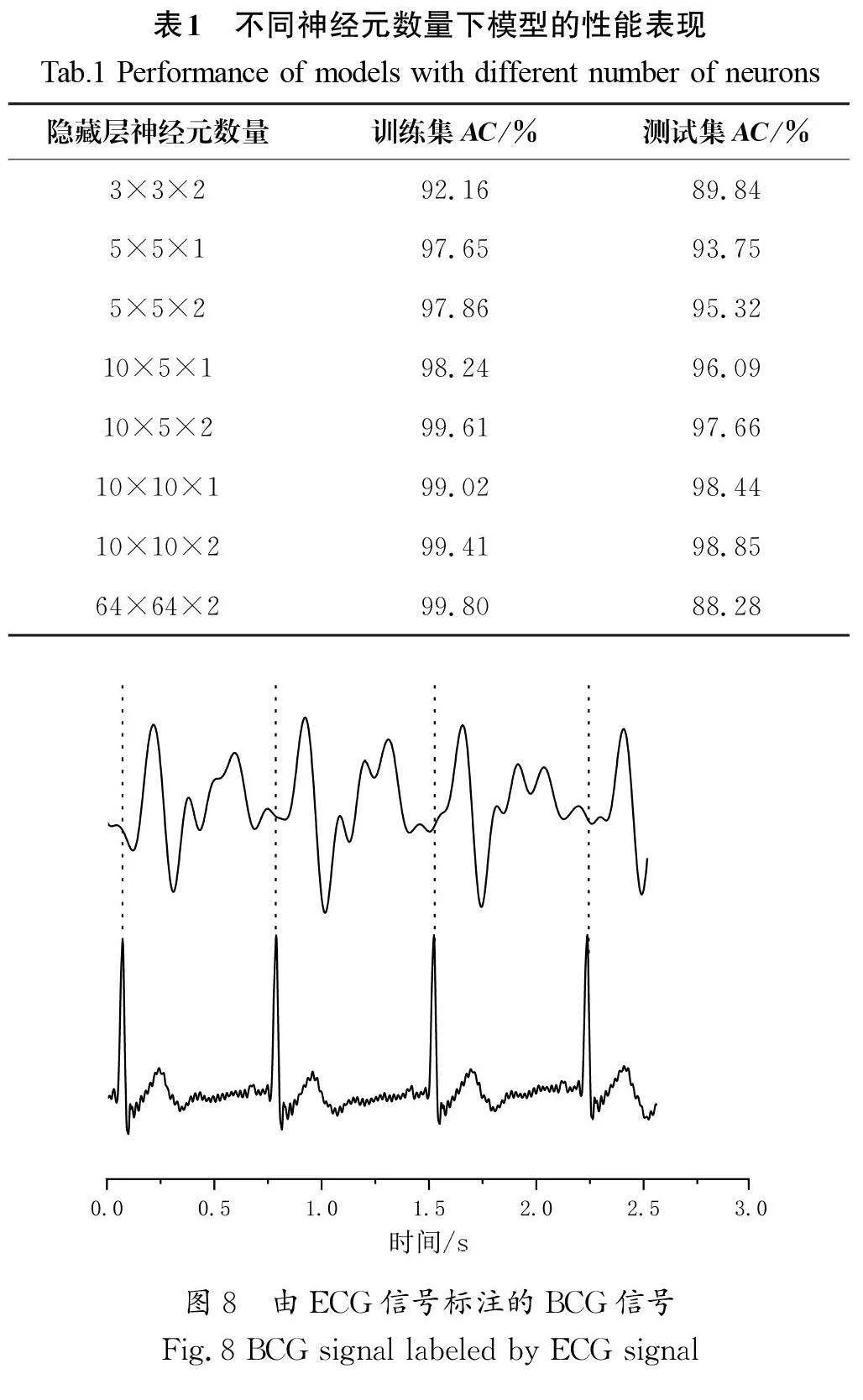
神经网络的输入层和输出层的节点设置相对简单。输入层的神经元数量取决于输入数据的变量数量，输出层神经元的数量可以设置为1，但是如何设置每层隐藏层的神经元数量相对复杂。如果隐藏层的神经元数量过少，会导致模型欠拟合，如果隐藏层的神经元数量过多，不仅会导致数据中的有限信息无法训练每一个神经元而使模型过拟合，同时会导致训练时间过长。从表1中可以清楚地看出，当神经元数量过少时，测试集准确率过低;当神经元数量过多时，模型出现了过拟合。因此，在本次实验中隐藏层的数量设置为10×10×2。

3 实验与分析（Experiments and analysis）

3.1 数据集的获取与划分

在本次实验中，同步采集了5位健康受试者的BCG信号和ECG信号用于验证本文提出的算法，其中有3名女性和2名男性，年龄在23～27岁，每位受试者数据长度约为5 min。通过同步采集的ECG信号将BCG信号划分为若干个子序列，其中包含完整心动周期片段（HB）和非心动周期片段（NHB），片段长度r 设置为450（每个时间序列为0.9 s）。由ECG信号标注的BCG信号如图8所示，图8中上方波形为BCG信号，下方波形为ECG信号。

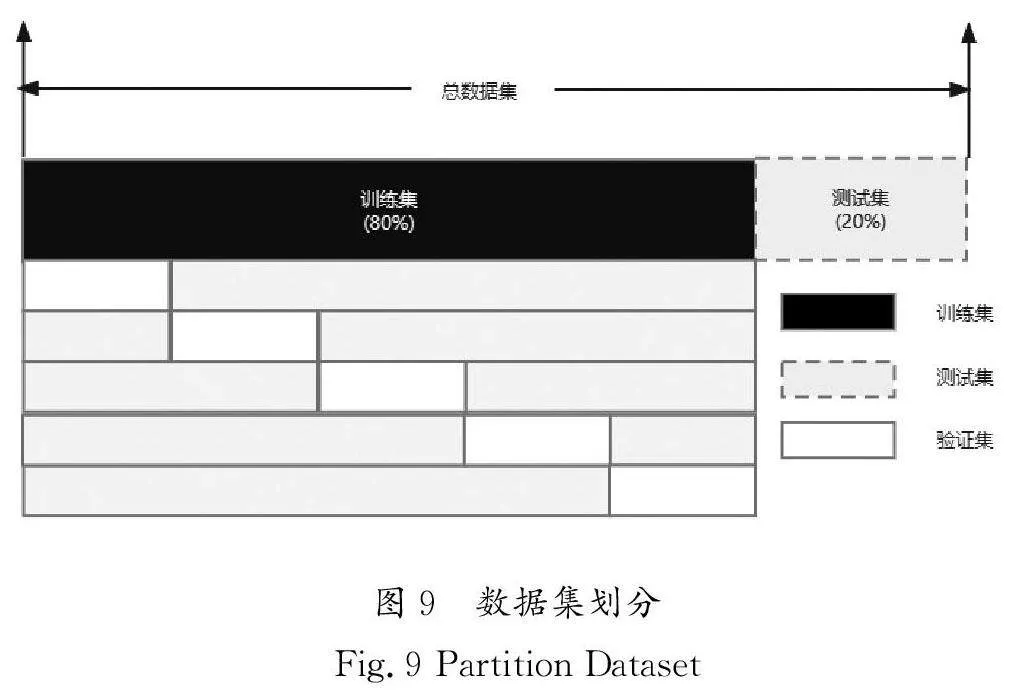
在数据集标注完成后，对其进行分割，将数据集划分为训练集和测试集（图9），其中80%的数据用于训练，20%的数据用于测试。训练集用于训练模型和更新模型参数，测试集用于评估模型并测试模型的最终性能，验证集用于观察模型的训练效果。

3.2 评价指标

评价指标可以反映模型的泛化能力，评估不同模型的性能，还可以用于模型优化。对于分类模型，混淆矩阵可以直观地计算出模型的准确性（AC）、F1分数、敏感性（SE）等指标。混淆矩阵的定义如公式（8）所示，其中TP是正确检测的HB的数量，FP是未检测到的NHB的数量，TN是正确检测到NHB的数量，FN是错过的HB的数量。AC反映了正确预测的样本的百分比，由公式（9）定义。SE是指检测到的正确HB的数量与所有HB的数量之比，如公式（10）所定义。F1分数又称平衡F 分数（Balanced Score），它被定义为精确率和召回率的调和平均数，如公式（11）中所定义，其中r 为召回率。

3.3 实验结果

本次实验的计算机配置如下：11th Gen Intel（R） Core（TM） i7-11700 @ 2.50 GHz 2.50 GHz，RAM 为16 GB，仿真环境为Python3.7。图10和图11分别为模型训练过程中训练集和验证集随着迭代次数的增加，其损失值和准确率的变化曲线。在前10次迭代中，随着验证集和训练集的损失值迅速下降，准确率则快速攀升，当迭代次数达到30次时，模型性能趋于稳定，最终确定迭代次数为30次。

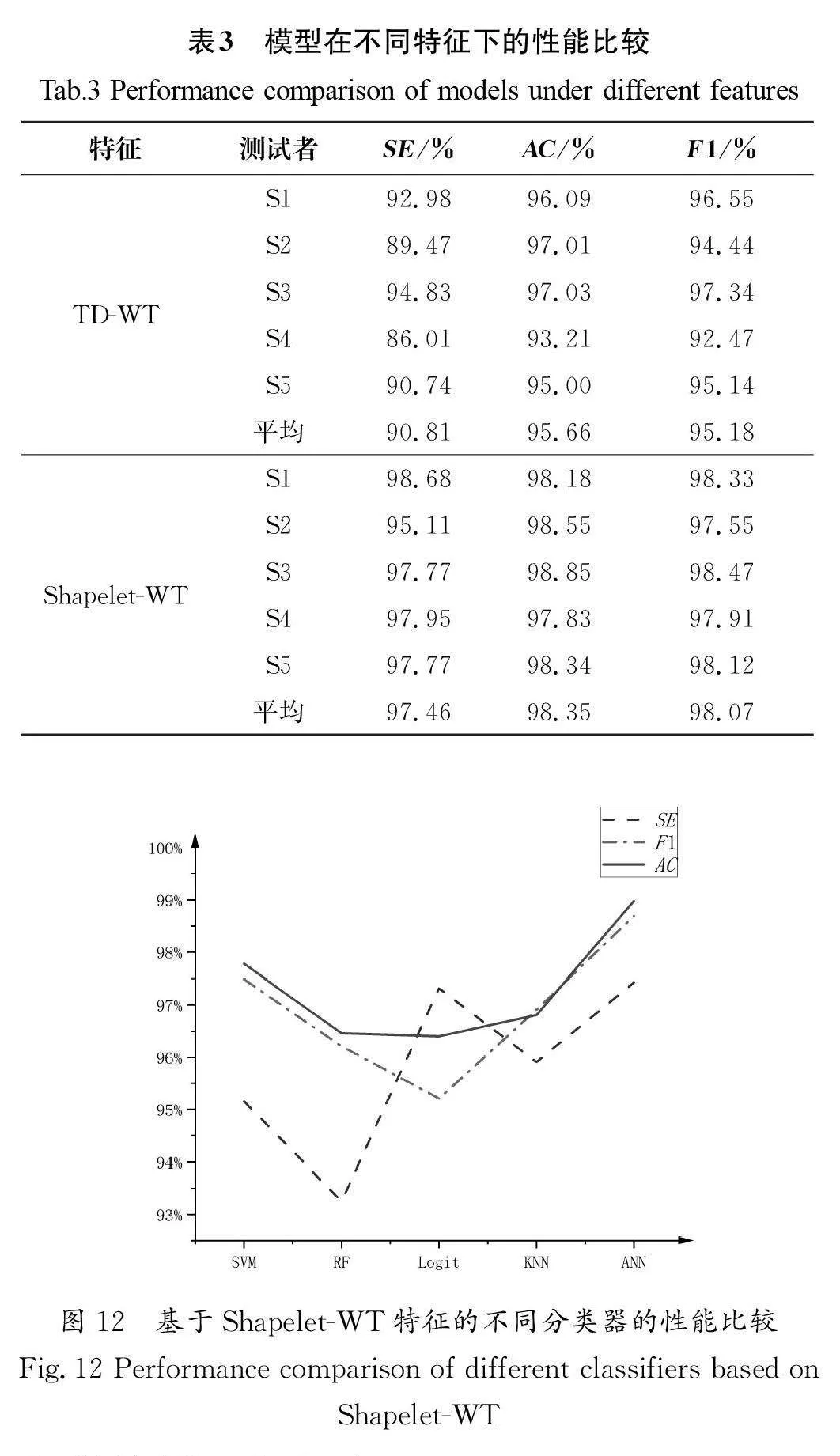
为了验证提取的Shapelet-WT特征更具鲁棒性，本研究也提取了BCG信号的时域特征，将时域特征与小波特征进行融合并命名为TD-WT特征，具体提取的时域特征如表2所示。模型使用不同特征进行心动周期检测的实验结果如表3所示，将输入到ANN中的TD-WT特征和Shapelet-WT特征进行比较，验证模型在不同特征下每位测试者心动周期的检测性能。通过添加每位测试者的混淆矩阵计算总体的AC、SE和F1分数，与TD-WT特征相比，使用Shapelet-WT特征显著提高了模型的整体性能，其中准确率高达98.35%，同时对于敏感性的大幅提升也反映了Shapelet-WT特征的显著性。

采用与文中相同的数据集及划分策略，研究人员对支持向量机（SVM）、随机森林（RF）、K-最近邻（KNN）、Logistic回归以及本文所提算法进行了性能对比。由图12可以看出，基于Shapelet-WT特征的ANN分类器在各个指标上都明显优于传统的分类器，预测的心动周期与实际心动周期高度重合证明了其在心动周期检测中的优越性。总体而言，本文提出的检测算法可以准确地检测到绝大多数的心动周期，并且对于受到体动等噪声影响的BCG信号，也获得了很好的心动周期检测精度，验证了该算法的鲁棒性。

4 结论（Conclusion）

本文提出了一种基于复杂特征的心动周期检测算法，提取BCG信号的Shapelet特征和小波变换多尺度特征，并在此基础上使用人工神经网络深度学习模型智能化地检测心动周期。其中，Shapelet特征主要用于弥补普通的时域特征无法很好地区分时间序列差异的缺陷，提取的小波特征则可以进一步完善遗漏的细节特征，同时提取了信号的时域特征用于对比验证。为了更加准确地检测心动周期，本研究摒弃了传统的分类器，采用ANN神经网络。实验结果表明，本文提取的复杂特征比传统特征更具鲁棒性，与传统算法相比，本文提出的算法显著提升了心动周期的识别准确率，具有优秀的检测效果，可以用于长期的家庭式健康监测。

作者简介：

朱永梁（1998-），男，硕士生。研究领域：BCG信号处理。

朱耀东（1970-），男，博士，教授。研究领域：智能计算机与健康物联网。

唐敏（1999-），女，硕士生。研究领域：智能健康机器人。

胡蝶（1998-），女，硕士生。研究领域：情绪识别。