基于EGARCH-M-CVaR模型的中证500股指期货风险测度研究

摘要：文章以2018-2022年中证500股指期货日收盘价作为研究对象，使用不同分布下的EGARCH-M模型对其对数收益率进行VaR测度和VaR失败率检验以选择最优模型，并利用最优模型进行CVaR测算和CVaR、VaR比较。结果表明：一是GED分布下的EGARCH-M模型可以更好地测度中证500股指期货风险，其为文章最优模型；二是99%置信水平下所求出的CVaR和VaR相较于95%置信水平下所求值可以更好地测度风险；三是在GED分布下的EGARCH-M模型下CVaR均值高于VaR均值，说明其可以更好地覆盖尾部风险，其测度效果优于VaR模型。

关键词：中证500股指期货;EGARCH-M模型;期货市场

中图分类号：F832.51文献标识码：A文章编号：1005-6432（2024）21-0000-05

[DOI]10.13939/j.cnki.zgsc.2024.21.010

1引言

股指期货作为金融衍生品的一种，虽具备价格发现和风险规避的优点，但高杠杆、保证金追加等风险也会使投资者造成巨大损失。我国股指期货市场发展时间晚于国外，应对股指期货风险的能力仍需加强，风险管理势在必行，而对其进行风险测度与预测是风险管理中的重要环节。

迄今为止沪深300股指期货是国内大部分股指期货风险管理研究的主要对象，而对中证500股指期货的研究少之又少，这是由于中证500股指期货的推出时间较晚，其2017年以前持仓量和成交量均远低于沪深300股指期货。但近几年中证500股指期货的日均成交量和持仓量均几近接近沪深300股指期货，在我国股指期货市场中正处于越来越重要的地位。鉴于此，开展中证500股指期货的风险测度研究具有很强的现实意义。

国外对于金融产品风险测度的研究较早，首当其冲就是使用VaR进行风险测度。VaR是摩根银行内部管理部门于20世纪80年代所提出，它是指金融资产在未来一段时间内在给定置信度水平下可能面临的最大损失，在90年代后获得广泛使用[1]。Kavussanos等运用VaR模型对新兴市场和发达市场的股票投资组合进行风险测度[2]。Lai等应用VaR模型对原油市场波动性水平进行研究，发现通过提高建模过程中的多频域和时域的准确性，测度结果的准确性也会进一步提高[3]。尽管VaR具有许多优势，但其不具备次可加性和无法有效监测尾部风险，使得风险测度的精准度降低。为此，Uryasev于2000年提出了CVaR的概念，即金融资产在给定置信度水平下实际损失超过VaR的条件均值[4]。CVaR弥补了VaR的缺陷，成为了如今更加广泛使用的方法。Degiannakis和Floros利用条件波动率估算出VaR和CVaR的值，发现CVaR更能覆盖市场风险[5]。Drakos和Kouretas利用CVaR模型对2007年金融危机后股票市场的系统性风险进行了测度[6]。Pellegrini等利用CVaR模型对英国货币基金市场的系统性风险进行了测度[7]。以上研究只单纯运用VaR模型或CVaR模型进行研究，测度效果终究有限，而加入风险波动率的衡量后测度效果会再度提高。JeremicZoran等利用GARCH-VaR模型对2005-2015年塞尔维亚资本市场的风险进行评估，结果发现对称GARCH模型的VaR结果在99%置信水平下最佳[8]。NunoSobreira和RuiLouro运用GARCH模型预测葡萄牙股票市场的风险值和预期损失，发现非对称GARCH模型在预测VaR方面效果更好[9]。Karmakar和Paul从高频数据出发，运用CGARCH-EVT-Copula模型去预测三个不同市场的三对股票价格指数日内投资组合的VaR和CVaR的值，发现CVaR的预测效果更好[10]。

国内相关研究起步较晚，所采用的方法与国外类似。姚凤阁等运用GARCH-CVaR模型对开放式股票型基金进行测度，发现在t分布下测度效果最好[11]。刘倩和李洁运用GARCH-VaR和GARCH-CVaR模型对货币基金进行风险测度，发现在同一分布下GARCH-CVaR模型的测度效果优于GARCH-VaR模型[12]。申利在方差-协方差、历史模拟和蒙特卡洛模拟三种测算VaR方法的基础上构建GARCH-VaR模型对外汇风险进行度量，得出在t分布下GARCH模型的测度结果最优的结论[13]。吕东杰比较不同分布下GARCH-CVAR模型对投资基金风险测度的效果，发现GARCH-GED-CVaR模型的测度效果最好[14]。徐伟民和肖坚采用GARCH-VAR模型测度中国碳金融交易价格风险，发现中国碳金融交易价格总体风险水平较高，上海与北京是风险最高的两大交易市场[15]。马慧子等基于g-VaR模型，运用求解倒向随机微分方程的Euler隐格式、C-N格式和预估校正法进行互联网金融风险测度并进行比较，得出预估校正法运算效率与精准度最高的结论[16]。李冠旭运用T-GARCH-VaR模型研究我国碳交易市场价格波动风险，发现风险波动集群效应与VaR波动程度之间具有明显同步性[17]。

综合上述研究，笔者发现GARCH-CVaR模型被国内外学者所认可，是较好的金融产品风险测度方法，但在国内的股指期货风险管理研究中对中证500股指期货研究较少。因此，文章将对中证500股指期货进行VaR测度并对测度结果进行比较分析，最后选出最佳测度模型来测算CVaR并与其测度的VaR进行比较。文章所得出结论会丰富相关研究内容并为后续学者进行相关研究时提供借鉴与参考。

2研究方法与数据说明

2.1模型构建

文章先使用EGARCH-M模型来计算波动率，此举的原因在于：（1）非对称的GARCH模型测度效果更好，而EGARCH模型满足非对称性质；（2）在条件均值模型中加入GARCH项的标准差形式可以使模型测度准确率再度提高[18-19]。所构建的EGARCH（p，q）-M模型表达式如下[20-21]：

其中，为中证500股指期货收益率，为收益率的无条件期望值，反映了风险和收益之间的替代关系，为残差，为随时间变化的条件方差，为独立同分布的随机变量，与相互独立且的条件方差等于，为滞后参数，为方差参数。表示金融市场中价格的非对称影响，当时，各种干扰对价格的影响是非对称的；当时，价格波动受到负外部冲击的影响大于受到正外部冲击的影响，此时称为“杠杆效应”；当时，情况相反。

之后利用上述模型测算出的条件标准差测算VaR和CVaR，表达式如下：

式（2）-式（5）中，为置信度，为不同分布的置信水平下分位数，为自由度，为伽马函数，为尾部厚度参数，其值为。

2.2样本数据说明与统计分析

文章选择2018年1月2日至2022年12月30日的中证500股指期货每日收盘价作为样本数据，共计1217个，数据来源为中证指数有限公司官网。随后以该样本数据为基础计算其对数收益率以进行进一步分析，表达式如下：

其中，为时刻收盘价，为时刻收盘价。

使用R软件对该样本数据进行平稳性、正态性、自相关性和条件异方差检验，具体结果如表1所示。

从表1可以看出，中证500股指期货的对数收益率在样本区间内的均值为-0.006，说明中证500股指期货在样本区间内整体呈下降趋势。从偏度、峰度数值可以看出该对数收益率序列具有“尖峰肥尾”的特征。J-B统计量在1%的显著性水平下显著，拒绝服从正态分布假设，即该对数收益率序列不服从正态分布。从ADF统计量值可以看出其在1%显著性水平下显著，说明该对数收益率序列可拒绝序列为非平稳序列的原假设，即该序列为平稳序列。滞后10阶与20阶的Ljung-BoxQ统计量的p值均高于显著性水平5%，可认为该序列为纯随机序列，不具备长记忆性。

3实证分析

3.1EGARCH-M模型的拟合结果

EGARCH-M模型的拟合需要在时间序列具备ARCH效应的前提下进行，文章采用PortmanteauQ检验法检验出中证500股指期货对数收益率序列在滞后1阶至5阶时均在5%显著性水平下显著，说明该序列具备ARCH效应，可进行EGARCH-M模型拟合。

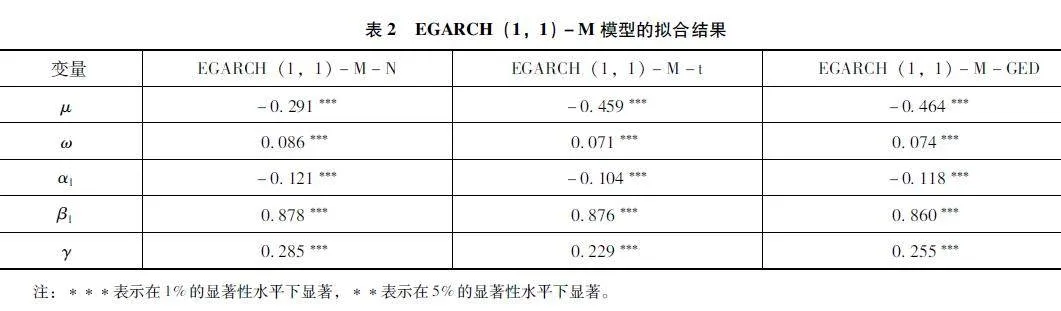
随后使用R软件对中证500股指期货的EGARCH-M模型在不同滞后阶数和分布下的AIC值进行测算，并依照AIC最小值原则进行定阶。测算结果表明：在正态分布、t分布和GED分布下，EGARCH-M模型的滞后阶数均在（1，1）时AIC值最小，因此三种分布均选用EGARCH（1，1）-M模型。不同分布下的EGARCH（1，1）-M模型拟合结果如表2所示。

从表2看出EGARCH（1，1）-M模型在不同分布下拟合效果均显著。具体来看，在不同分布下，GARCH（1，1）-M模型的与的和均小于1，说明波动具有较强持续性，因此利用当前数据来预测未来的条件方差是可行的。均显著说明中证500股指期货收益的条件波动率具有明显的杠杆效应。总而言之，不同分布下的EGARCH（1，1）-M模型之间并无明显的优势，需进行进一步的VaR测算和样本内检验才可获得最优模型。

3.2VaR测算与结果分析

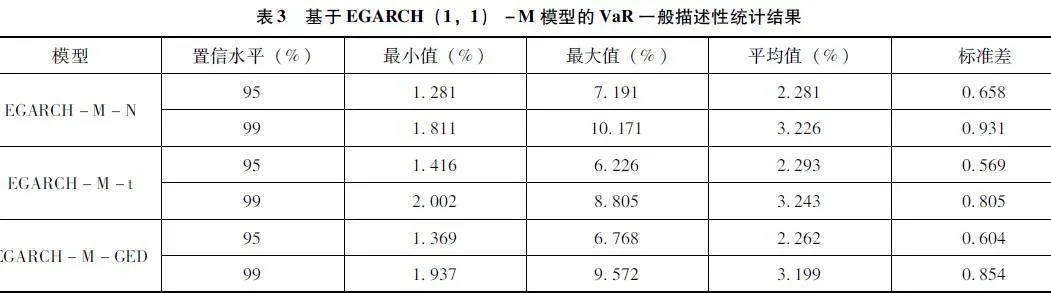
将上述拟合好的不同分布下EGARCH（1，1）-M模型中的条件标准差代入公式（2）中以测算样本数据的VaR，置信水平分别取95%和99%，测算结果如表3所示。

从表3可知，在EGARCH-M-N模型下，每天损失的均值在95%置信水平下为2.281%，即有95%的概率可将每天的风险损失控制在2.281%之内。在99%置信水平下为3.226%，即有99%的概率可将每天的风险损失控制在3.226%之内。最大值在95%置信水平下为7.191%，说明在该模型下有95%的概率将文章样本数据中的每日最大损失控制在7.191%以内。在99%置信水平下为10.171%，说明在该模型下有99%的概率将文章样本数据中的每日最大损失控制在10.171%以内。

在EGARCH-M-t模型下，每天损失的均值在95%置信水平下为2.293%，即有95%的概率可将每天的风险损失控制在2.293%之内。在99%置信水平下为3.243%，即有99%的概率可将每天的风险损失控制在3.243%之内。最大值在95%置信水平下为6.226%，说明在该模型下有95%的概率将文章样本数据中的每日最大损失控制在6.226%以内。在99%置信水平下为8.805%，说明在该模型下有99%的概率将文章样本数据中的每日最大损失控制在8.805%以内。

在EGARCH-M-GED模型下，每天损失的均值在95%置信水平下为2.262%，即有95%的概率可将每天的风险损失控制在2.262%之内。在99%置信水平下为3.199%，即有99%的概率可将每天的风险损失控制在3.199%之内。最大值在95%置信水平下为6.768%，说明在该模型下有95%的概率将文章样本数据中的每日最大损失控制在6.768%以内。在99%置信水平下为9.572%，说明在该模型下有99%的概率将文章样本数据中的每日最大损失控制在9.572%以内。

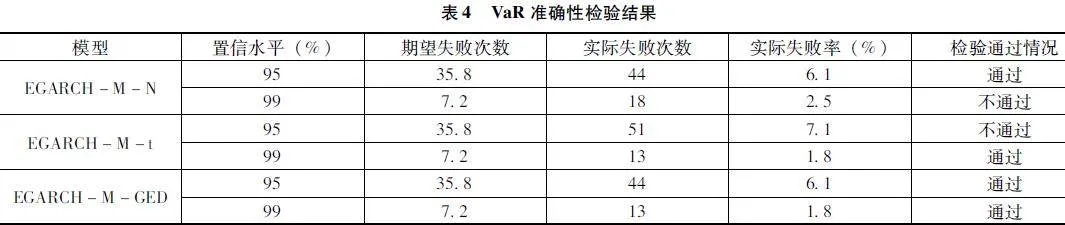
3.3VaR准确性检验

上述测算出的VaR总体在同一置信水平下较为接近，仍无法判断最优模型。因此对VaR的有效性和准确性进行检验。文章使用Kupiec失败率检验法进行检验。首先设置信度为，失败天数为，样本数量为，失败率为；而后建立原假设，备择假设。LR统计量表达式如下：

当接受原假设时，服从分布，即认为通过Kupiec失败率检验[15]。

对样本中的后716个VaR进行准确性检验，置信水平分别取95%和99%，具体结果如表4所示。从表4可以看出，在95%置信水平下t分布未通过Kupiec失败率检验，另两个分布均通过检验，而在99%置信水平下正态分布未通过检验，另两个分布均通过检验。实际失败率方面在95%置信水平下EGARCH-M-GED模型和EGARCH-M-N模型实际失败率均最低，在99%置信水平下EGARCH-M-GED模型和EGARCH-M-t模型实际失败率均最低。由于t分布和正态分布下的模型均出现检验不通过的情况，因此文章选择EGARCH-M-GED模型作为最优模型。

3.4CVaR测算与结果分析

将EGARCH-M-GED模型中的条件标准差代入公式（5）中以计算CVaR，置信水平分别取95%和99%，测算结果如表5所示。从表5可以看出，在EGARCH-M-GED模型下CVaR的均值要高于表3中VaR的均值，这是由于VaR无法更好地监测尾部风险所造成的。因此CVaR可以更好地覆盖并识别尾部风险。

4结论与建议

文章通过研究得出如下结论：

1.中证500股指期货具备“尖峰厚尾”的特征，这与大多数研究所得出的结论相同。此外，经过EGARCH-M模型拟合后发现中证500股指期货条件波动率具备杠杆效应。

2.通过进行Kupiec失败率检验，发现在95%置信水平和99%置信水平下EGARCH-M-GED模型均通过检验且实际失败率均最低，是文章的最优模型，其可以很好地拟合中证500股指期货的每日收盘价对数收益率。

3.99%置信水平下所求出的VaR和CVaR总体上均大于95%水平下所求出的VaR和CVaR，说明99%置信水平下qMICItotonBPKRoLuXzEdg==风险测度的效果良好。

4.虽然VaR可以更好地量化风险，但其无法充分监测尾部风险的缺陷从CVaR均值大于VaR均值中发现，再度说明CVaR在测度风险上的优越性。

针对我国金融市场现状，文章给出三点建议：（1）各监管部门在进行风险管理时应当多元化使用风险管理工具和风险测度工具以更准确地测度风险并精准提出预防措施；（2）投资者也应当运用自身专业知识和经验多元化使用风险测度工具以达到自身规避风险的目的；（3）政策制定部门应当根据当前我国金融市场的发展情况和世界经济形势选择适合自身的金融市场制度，这么做也可以更好地减少金融市场风险。

参考文献：

• 鹿志强.基于双线性GARCH-CVaR模型的人民币汇率风险测度研究[D].兰州：兰州理工大学，2020.
• DIMITRAKOPOULOSDN，KAVUSSANOSMG，SPYROUSSI.Valueatriskmodelsforvolatileemergingmarketsequityportfolios[J].TheQuarterlyReviewofEconomicsandFinance，2010，50（4）：515-526.
• HEK，LAIKK，YENJ.Value-at-riskestimationofcrudeoilpriceusingMCAbasedtransientriskmodelingapproach[J].EnergyEconomics，2011，33（5）：903-911.
• URYASEVS.Conditionalvalue-at-risk：optimizationalgorithmsandapplications[C]//ConferenceonComputationalIntelligenceforFinancialEngineering.IEEE，2000.
• DEGIANNAKISS，FLOROSC.Modellingandforecastinghighfrequencyfinancialdata[J].PalgraveMacmillanUK，2015.
• DRAKOSAA，KOURETASGP.Bankownership，financialsegmentsandthemeasurementofsystemicrisk：AnapplicationofCoVaR[J].InternationalReviewofEconomics&Finance，2015，40：127-140.
• PELLEGRINICB，MEOLIM，URGAG.Moneymarketfunds，shadowbankingandsystemicriskinUnitedKingdom[J].FinanceResearchLetters，2017，21.
• JeremićZoran，TerzićIvica，MilojevićMarko.ValueatriskestimationandvalidationintheSerbiancapitalmarketintheperiod2005-2015[J].Bankarstvo，2016，45（1）.
• NUNOS，RUIL.EvaluationofvolatilitymodelsforforecastingValue-at-RiskandExpectedShortfallinthePortuguesestockmarket[J].FinanceResearchLetters，2019.
• KARMAKARM，PAULS.IntradayportfolioriskmanagementusingVaRandCVaR：ACGARCH-EVT-Copulaapproach[J].InternationalJournalofForecasting，2019，35（2）：699-709.
• 姚凤阁，刘超群，张蒙.基于GARCH-CVaR模型的开放式股票型基金的市场风险度量研究[J].齐齐哈尔大学学报（哲学社会科学版），2016（10）：16-20.
• 刘倩，李洁.基于GARCH-VaR和GARCH-CVaR模型的货币基金产品风险研究[J].经济研究导刊，2019（21）：82-83.
• 申利.基于GARCH-VaR模型的外汇风险度量方法的统计比较[J].统计与决策，2018，34（21）：163-166.
• 吕东杰.基于GARCH-CVAR模型对投资基金风险测度的理论分析与实证研究[J].现代经济信息，2018（18）：291-292.
• 徐伟民，肖坚.中国碳金融交易价格风险测度研究——基于GARCH-VaR模型视角[J].金融教育研究，2022，35（6）：3-10.
• 马慧子，刘翠翠，林琳等.互联网金融风险测度与数值分析——基于g-VaR模型[J].山东科技大学学报（自然科学版），2022，41（2）：80-88.
• 李冠旭.基于T-GARCH-VaR模型的我国碳交易市场价格波动风险测度研究[D].北京：对外经济贸易大学，2022.
• 鹿志强.基于双线性GARCH-CVaR模型的人民币汇率风险测度研究[D].兰州：兰州理工大学，2020.

[19]徐伟民，肖坚.中国碳金融交易价格风险测度研究——基于GARCH-VaR模型视角[J].金融教育研究，2022，35（6）：3-10.

[20]马慧子，刘翠翠，林琳等.互联网金融风险测度与数值分析——基于g-VaR模型[J].山东科技大学学报（自然科学版），2022，41（2）：80-88.

[21]李冠旭.基于T-GARCH-VaR模型的我国碳交易市场价格波动风险测度研究[D].北京：对外经济贸易大学，2022.

作者简介：李闻宇（1998—），男，江苏南京人，硕士，研究方向：绿色金融与低碳发展。