锈蚀冷弯薄壁型钢柱弹性整体屈曲分析

聂彪 徐善华 陈华鹏 胡伟成 肖林发

收稿日期：2023-09-26

基金项目：国家自然科学基金项目（52308313，52208168）；江西省自然科学基金项目（20224BAB214067）；中国博士后科学基金                      资助项目（2023M741161）；江西省重点研发计划项目（20223BBH80002）

文章编号：1005-0523（2024）03-0010-10

摘要： 【目的】研究锈蚀冷弯薄壁型钢柱弹性整体屈曲性能。【方法】采用有限元特征值屈曲分析的方法，研究锈蚀部位、锈蚀区域长度和宽度对冷弯薄壁型钢柱弹性整体屈曲性能的影响，提出锈蚀冷弯薄壁型钢柱弹性整体屈曲应力计算方法，并对比分析理论计算结果与有限元特征值屈曲分析值。【结果】结果表明：随着锈蚀程度增大，弹性弯曲屈曲应力和弹性弯扭屈曲应力均逐渐下降；腹板锈蚀对弹性弯曲屈曲应力的影响大于翼缘锈蚀，而腹板锈蚀与翼缘锈蚀对弹性弯扭屈曲应力的影响接近。【结论】弹性弯曲屈曲应力随锈蚀区域长度增大逐渐下降，且下降速率呈减小趋势，而弹性弯扭屈曲应力随锈蚀区域长度增大近似线性下降；随着锈蚀区域宽度增大，弹性弯扭屈曲应力下降速率增大趋势大于弹性弯曲屈曲应力。

关键词：锈蚀；冷弯薄壁型钢；整体屈曲；有限元分析；弹性

中图分类号：TU318 文献标志码：A

本文引用格式：聂彪，徐善华，陈华鹏，等. 锈蚀冷弯薄壁型钢柱弹性整体屈曲分析[J]. 华东交通大学学报，2024，41（3）：10-19.

Elastic Overall Buckling Analysis of Corroded Cold-Formed

Thin-Walled Steel Columns

Nie Biao1， Xu Shanhua2， Chen Huapeng1， Hu Weicheng1， Xiao Linfa1

（1. School of Transportation Engineering， East China Jiaotong University， Nanchang 330013， China;

2. School of Civil Engineering， Xi'an University of Architecture & Technology， Xi'an 710055， China）

Abstract： 【Objective】The overall elastic buckling performance of corroded cold-formed thin-walled steel columns was investigated in this paper. 【Method】The finite element eigenvalue buckling analysis method was used to study the effects of corrosion location， corrosion area length and width on the elastic overall buckling of cold-formed thin-walled steel columns. The calculation method for the elastic overall buckling stress of corroded cold-formed thin-walled steel columns was proposed， and the theoretical calculation results were compared with the finite element eigenvalue buckling analysis values. 【Result】The results show that as the degree of corrosion increased， the elastic bending buckling stress and the elastic bending torsional buckling stress gradually decreased. The effect of web corrosion on elastic bending buckling stress was greater than that of flange corrosion，while the effect of web corrosion and flange corrosion on elastic bending torsional buckling stress was similar. The elastic bending buckling stress gradually decreased with the increase of the corrosion area length， and the rate of decrease showed a decreasing trend. However， the elastic bending torsional buckling stress approximately linearly decreased with the increase of the corrosion area length. 【Conclusion】With the increase of the corrosion area width， the elastic bending torsional buckling stress decreased faster than the elastic bending buckling stress.

Key words： corrosion; cold-formed thin-walled steel; overall buckling; finite element analysis; elastic

Citation format： NIE B， XU S H， CHEN H P， et al. Elastic overall buckling analysis of corroded cold-formed thin-walled steel columns[J]. Journal of East China Jiaotong University， 2024， 41（3）： 10-19.

【研究意义】本研究对于保障冷弯薄壁型钢结构在腐蚀环境下的安全服役具有重要意义。通过及时评估锈蚀构件的残余承载力，发现安全隐患，可以最大限度地避免因锈蚀引发的结构破坏事故。

【研究进展】冷弯薄壁型钢构件通过改变截面形式、冷作硬化作用增大其惯性矩[1-3]和强度[4-5]，与传统的热轧钢相比，具有经济环保、易于加工等优点，因此，不仅被广泛应用于柱（墙）、梁、桁架、网架等主要承重构件，而且也被用于檩条、墙梁（柱）、屋面板、墙板等次要受力构件[6-8]。然而，许多冷弯薄壁型钢结构工程在高湿度、高氯离子或硫酸根离子等腐蚀环境下服役时，往往难以通过防护和构造措施避免锈蚀，存在严重的锈蚀问题。锈蚀导致钢结构承载性能退化，成为钢结构工程服役过程中主要的安全隐患[9]。

冷弯薄壁型钢结构具有壁厚小、构件细长、截面非双轴对称等特点，易发生局部屈曲、畸变屈曲和整体屈曲，因此，其稳定性能一直是结构工程领域研究的热点问题。目前冷弯薄壁型钢构件稳定承载力计算方法主要有效宽度法和直接强度法，而屈曲临界荷载是其无法回避的参数。为此，国内外学者针对未锈蚀冷弯薄壁型钢柱弹性屈曲开展了大量研究，取得了较多创新性成果[10-16]。目前，鲜有文献开展锈蚀冷弯薄壁型钢柱弹性屈曲研究，与此相近的研究主要集中在开孔冷弯薄壁型钢柱弹性屈曲方面。Moen等[17-19]通过有限元特征值屈曲分析，研究了开孔对冷弯薄壁型钢构件屈曲模态和屈曲临界荷载的影响，结果表明，腹板开孔长度和宽度均对局部屈曲模态有影响，导致局部屈曲临界荷载下降，而对畸变屈曲、整体屈曲模态和临界荷载影响均较小。姚永红等[20-21]通过大量的数值分析获得不同截面开孔冷弯薄壁型钢构件的弹性屈曲特性，结果表明，开孔构件主要出现两种形式的局部屈曲模态，开孔对畸变屈曲临界荷载影响较大，而对其半波长影响不明显，开孔对整体屈曲模态和屈曲临界荷载影响均较小。

由于截面特性改变，现有屈曲临界荷载计算方法，如理论计算方法、有限条法、广义梁法等，不再适用于开孔冷弯薄壁型钢构件。Smith等[22]对开孔冷弯薄壁型钢构件弹性屈曲性能进行了理论分析，建立了采用有限条法计算开孔构件屈曲临界荷载的简化方法。而Casafont等[23]认为Smith等[22]提出的通过开孔板刚度折减厚度的方法计算屈曲临界荷载并不精确，而后采用回归拟合得到了开孔构件折减厚度的计算公式，并通过有限元分析验证了该方法的可靠性。而后Casafont等[24]又提出两种不同性能的梁单元表示孔洞部位和非孔洞部位，改进了现有广义梁法，使其适用于计算开孔冷弯薄壁型钢构件屈曲临界荷载。以上研究表明，开孔对冷弯薄壁型钢构件弹性屈曲性能有明显影响。开孔与腐蚀损伤均导致构件截面特性改变，两者对冷弯薄壁型钢构件弹性屈曲性能的影响存在一定的共性。但是锈蚀冷弯薄壁型钢构件弹性屈曲性能研究还处于空白。

【创新特色】本文采用有限元特征值屈曲分析的方法，研究了锈蚀部位、锈蚀区域长度和宽度对冷弯薄壁型钢柱弹性整体屈曲的影响。【关键问题】揭示了弹性冷弯薄壁型钢柱整体屈曲应力随锈蚀参数的退化规律，提出了锈蚀冷弯薄壁型钢柱弹性整体屈曲应力计算方法。

1    数值分析

1.1    有限元模型

目前冷弯薄壁型钢构件弹性屈曲数值分析方法主要有限条法、广义梁法和有限元法，由于锈蚀冷弯薄壁型钢表面不规则，常用的有限条法和广义梁法不能直接用于其弹性屈曲分析，因此，本文采用有限元法研究锈蚀冷弯薄壁型钢柱弹性整体屈曲性能。本文基于有限元软件Abaqus建立锈蚀冷弯薄壁型钢柱有限元模型。采用S8R5简化积分8节点薄壳单元，收敛性分析结果表明单元尺寸4 mm时结果较合理。边界条件参考文献[18]，约束两端节点x和y方向自由度和中间截面节点z方向自由度，均匀荷载分别加载在钢柱两端。弹性模量采用未锈蚀平板试件弹性模量[25]，泊松比取0.3。采用有限元特征值屈曲分析的方法得到锈蚀冷弯薄壁型钢柱弹性整体屈曲应力。

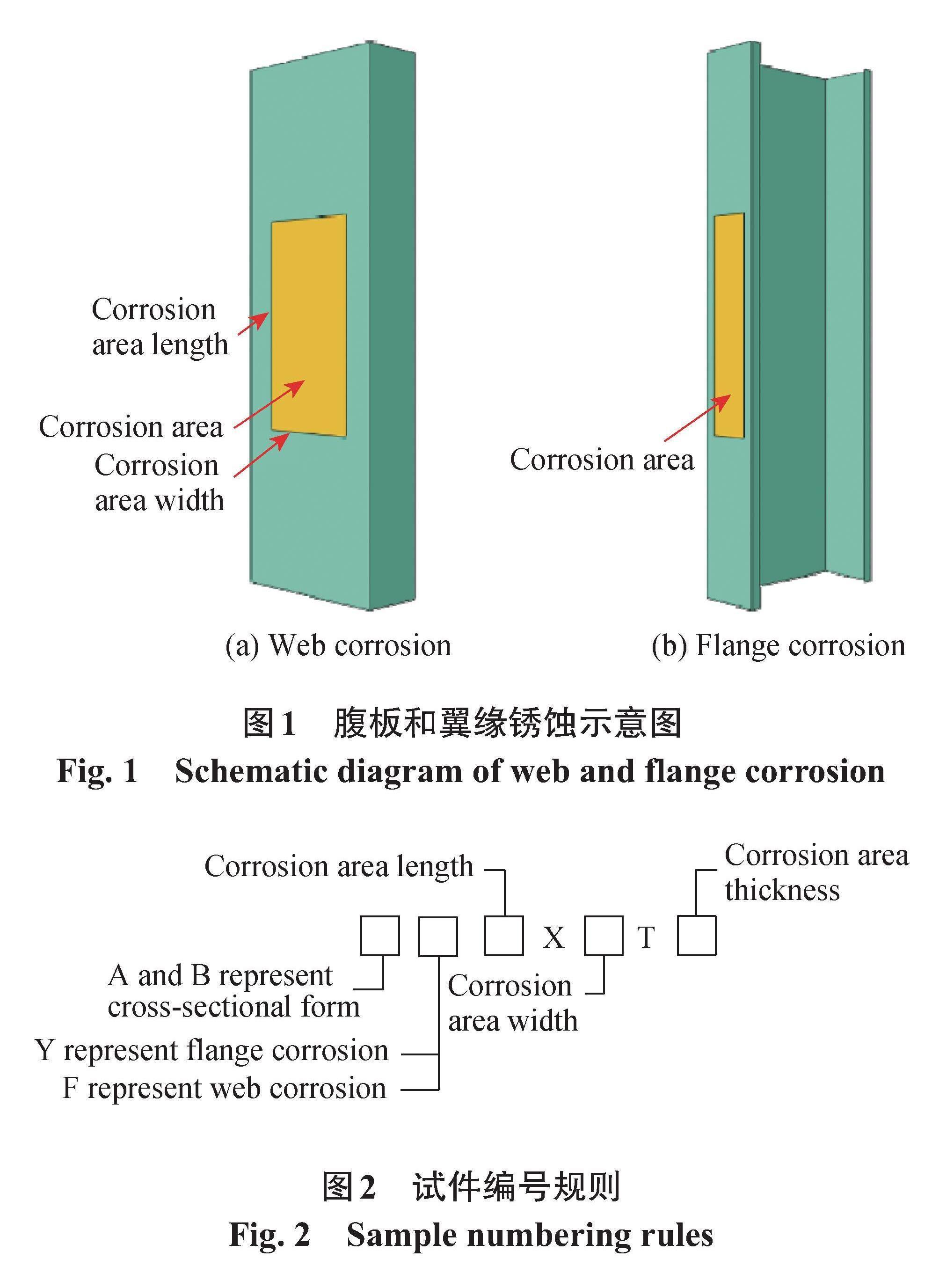
本文假设锈蚀区域为规则矩形，通过减少锈蚀区域厚度表示锈蚀程度，如图1所示。根据分析发现卷边锈蚀对冷弯薄壁型钢整体屈曲应力影响较小，因此，本文主要研究腹板与翼缘锈蚀的影响。本文选取了两种截面和多种锈蚀区域厚度，锈蚀区域位置均在钢柱中间高度，试件原始厚度均为2 mm。图2给出了试件编号规则，其中A类型截面的柱腹板，翼缘，卷边宽度和长度分别为100，60，20，2 000 mm；B类型截面的柱腹板，翼缘，卷边宽度和长度分别为80，40，10，1 600 mm。

1.2 参数分析

冷弯薄壁型钢柱整体屈曲主要包括弯曲屈曲和弯扭屈曲。弯曲屈曲是指绕截面非对称轴（弱轴）弯曲，截面形状不变，只产生侧移；扭转屈曲是指绕截面对称轴（强轴）弯曲的同时又绕截面剪心纵轴扭转，截面形状不变，产生侧移和扭转角。因此，本文参数分析主要研究锈蚀对冷弯薄壁型钢柱弯曲屈曲应力和弯扭屈曲应力的影响。

1.2.1 锈蚀部位的影响

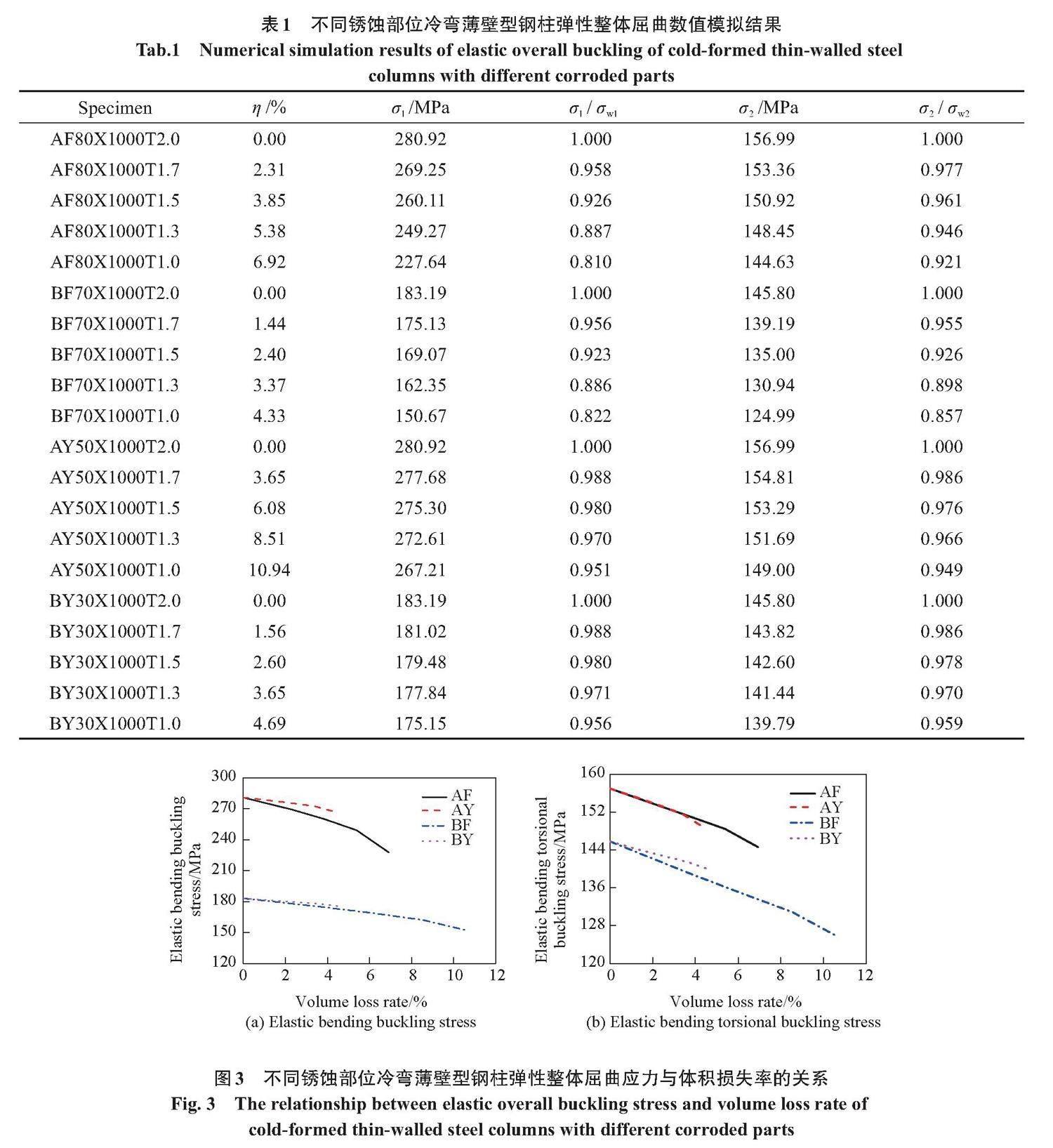
表1给出了不同锈蚀部位冷弯薄壁型钢柱弹性整体屈曲数值模拟结果。其中[η]表示体积损失率；[σ1]和[σ2]分别表示弯曲屈曲应力和弯扭屈曲应力； [σw1]和[σw2]分别为未锈蚀试件弯曲屈曲应力和弯扭屈曲应力。为了对比腹板和翼缘锈蚀对冷弯薄壁型钢柱弹性整体屈曲应力的影响，图3给出了不同锈蚀部位冷弯薄壁型钢柱弹性整体屈曲应力与体积损失率的关系。由表1和图3（a）可以发现，对于A类型截面腹板锈蚀的钢柱，体积损失率2.31%，3.85%，5.38%和6.92%的柱弹性弯曲应力分别下降了4.15%，7.41%，11.26%和18.96%，说明随着锈蚀程度的增大，弹性弯曲应力逐渐下降，并且下降速率有增大趋势，主要原因是腹板锈蚀造成锈蚀区域截面惯性矩减小而不改变构件长度，导致构件长细比下降。另外，随着锈蚀区域厚度下降，钢柱板件宽厚比增大，钢柱趋向产生局部屈曲，因此，锈蚀达到一定程度后，受局部屈曲的影响，弹性弯曲屈曲应力下降速率增大。对比腹板和翼缘锈蚀的柱可以发现，腹板锈蚀的柱弹性弯曲屈曲应力下降速率明显大于翼缘锈蚀，且两者差距随着体积损失率增大不断增大，如图3（a）所示。这是因为一方面，腹板锈蚀对惯性矩的影响大于翼缘锈蚀，另一方面，腹板锈蚀区域更宽，宽厚比更大，受局部屈曲影响更大。由表1和图3（b）可以发现，随着体积损失率增大，两类截面形式柱弹性弯扭屈曲应力不断下降，并且下降速率有增大趋势。对于体积损失率6.92%的A类型截面腹板锈蚀的钢柱，弹性弯曲屈曲应力下降了18.96%，而弹性弯扭屈曲应力下降了7.88%，说明腹板锈蚀对弹性弯曲屈曲应力的影响大于弹性弯扭屈曲应力。对于体积损失率4.69%的B类型截面翼缘锈蚀的钢柱，弹性弯曲屈曲应力下降了4.39%，而弹性弯扭屈曲应力下降了4.12%，说明翼缘锈蚀对弹性弯曲屈曲应力和弹性弯扭屈曲应力的影响接近。

1.2.2 锈蚀区域长度的影响

表2给出了不同锈蚀区域长度冷弯薄壁型钢柱弹性整体屈曲数值模拟结果。图4给出了锈蚀冷弯薄壁型钢柱弹性整体屈曲应力与锈蚀区域长度的关系。由图4（a）可以发现，所有试件弹性弯曲屈曲应力随锈蚀区域长度增大逐渐下降，并且下降速率有减小趋势，主要原因是弯曲屈曲主要产生在试件中间，锈蚀区域越靠近端部对弯曲屈曲影响越小。对比腹板和翼缘锈蚀的柱可以发现，腹板锈蚀的柱弹性弯曲屈曲应力随锈蚀区域长度增大下降速率大于翼缘锈蚀的柱。由图4（b）可以发现，所有试件弹性弯扭屈曲应力随锈蚀区域长度增大近似线性下降，说明锈蚀区域位置对弹性弯扭屈曲应力影响较小。对比腹板和翼缘锈蚀的柱可以发现，腹板锈蚀区域长度对弹性弯扭屈曲应力的影响大于翼缘锈蚀区域长度。对于B类型截面的钢柱，翼缘锈蚀区域长度由600 mm增大到1 200 mm，弹性弯曲屈曲应力下降了1.59%，而弹性弯扭屈曲应力下降了2.59%，说明翼缘锈蚀区域长度对弹性弯曲屈曲应力的影响小于弹性弯扭屈曲应力。

1.2.3 锈蚀区域宽度的影响

表3给出了不同锈蚀区域宽度冷弯薄壁型钢柱弹性整体屈曲数值模拟结果。图5给出了锈蚀冷弯薄壁型钢柱弹性整体屈曲应力与锈蚀区域宽度的关系。由5（a）可以发现，所有试件弹性弯曲屈曲应力随锈蚀区域宽度增大逐渐下降，并且下降速率有增大趋势，主要原因随着锈蚀区域宽度增大，板件宽厚比增大，钢柱趋向产生局部屈曲，因此，锈蚀区域宽度达到一定值后，试件产生整体-局部相关屈曲，弹性弯曲屈曲应力下降速率增大。B类型截面的钢柱在腹板锈蚀宽度70 mm时弹性弯曲屈曲应力迅速下降，通过屈曲模态分析可以发现钢柱产生了较大的局部屈曲变形。主要原因是板件厚度减小对局部屈曲影响更大，随着宽厚比增大，未锈蚀产生整体屈曲的试件会趋向于产生局部屈曲。对比腹板和翼缘锈蚀的柱可以发现，腹板锈蚀的柱弹性弯曲屈曲应力随锈蚀区域宽度增大下降速率大于翼缘锈蚀的柱。由图5（b）可以发现，所有试件弹性弯扭屈曲应力随锈蚀区域宽度增大逐渐下降，并且下降速率有增大趋势。对比图5（a）和图5（b）可以发现，弹性弯扭屈曲应力随锈蚀区域宽度增大下降速率增大趋势大于弹性弯曲屈曲应力。

2 弹性整体屈曲应力计算方法

通过数值模拟分析发现，锈蚀冷弯薄壁型钢柱弯曲屈曲和弯扭屈曲变形特性基本与未锈蚀冷弯薄壁型钢柱一致。本文认为锈蚀冷弯薄壁型钢柱变形特征符合整体屈曲基本特性，如图6所示。

首先对弹性弯曲屈曲应力进行分析，图7给出了锈蚀冷弯薄壁型钢柱弹性弯曲屈曲应力计算模型。根据能量守恒原理，柱的总势能为应变能和外力势能之和

[Π=U+V]        （1）

式中：[Π]为钢柱总势能；[U]为钢柱应变能；[V]为钢柱外力势能。

锈蚀钢柱的应变能和外力势能分别为

[U=120l1EI1d2vdx2dx+12l1l2EI2d2vdx2dx+12l2l3EI1d2vdx2dx] （2）

[V=-120l3Pdvdx2dx]    （3）

式中：[E]为钢柱弹性模量；[I1]和[I2]分别为未锈蚀钢柱截面和锈蚀钢柱截面绕弱轴惯性矩；[l1]，[l2]和[l3]分别为柱低到锈蚀区域底部长度、柱低到锈蚀区域上部长度和柱长；[P]为荷载。

假定变形函数为

[v=B1sinπxl3]       （4）

式中：[v]为变形函数；[B1]为变形函数参数。

将式（4）代入式（2）和式（3）简化可得

[U=EI1B21π42l43l32+l12-l22+l3β4π+EI2B21π42l43l22-l12-l3β4π]  （5）

[V=-PB21π24l3]         （6）

其中：[β=sin2πl2l3-sin2πl1l3]。

根据势能驻值原理求解弹性弯曲屈曲荷载，即[dΠdB1=0]，可以得弹性弯曲屈曲荷载为

[Pcry=Eπ2Iyηl23]          （7）

式中：[Pcry]为弹性弯曲屈曲荷载；[Iyη]为锈蚀钢柱截面绕弱轴等效惯性矩，其表达式为

[Iyη=I1l3+l1-l2+l3β2π+I2l2-l1-l3β2πl3] （8）

由式（7）可以得到锈蚀钢柱绕弱轴弯曲屈曲临界应力

[σcry=PcryA=Eπ2Iyηl23A]     （9）

式中：[A]为钢柱截面面积。

未锈蚀钢柱弯扭屈曲临界应力计算式为

[σcrxw=σcrx+σcrw-σcrx+σcrw2-4σcrxσcrw1-x0i022A1-x0i02]（10）

式中：[σcrxw]为弯扭屈曲临界应力；[σcrx]为绕强轴的弯曲屈曲临界应力；[σcrw]为扭转屈曲临界应力；[x0]为截面剪心与形心之间的距离；[i0]为极回转半径。[Ix]为x方向惯性矩；[Iw]为扇形惯性矩；[It]为抗扭惯性矩。对于锈蚀冷弯薄壁型钢柱弯扭屈曲临界应力，本文参照式（6）对截面参数[Ix]，[Iw]和[It]进行修正，得到截面参数[Ix]，[Iw]和[It]表达式为

[Ixη=Ix1l3+l1-l2+l3β2π+Ix2l2-l1-l3β2πl3] （11）

[Iwη=Iw1l3+l1-l2+l3β2π+Iw2l2-l1-l3β2πl3] （12）

[Itη=It1l3+l1-l2+l3β2π+It2l2-l1-l3β2πl3] （13）

式中：[Ixη]，[Iwη]和[Itη]分别为锈蚀钢柱截面强绕轴等效惯性矩，等效扇形惯性矩和等效抗扭惯性矩；[Ix1]和[Ix2]分别为未锈蚀截面和锈蚀截面绕强轴惯性矩；[Iw1]和[Iw2]分别为未锈蚀截面和锈蚀截面扇形惯性矩；[It1]和[It2]分别为未锈蚀截面和锈蚀截面抗扭惯性矩。

3 弹性整体屈曲应力计算结果与有限元结果对比

为了验证整体屈曲应力理论计算结果的正确性，选取了4类试件：AF70X1000、AY50X1400、BF70X1000和BY30X1200。图8和图9给出了弹性整体屈曲应力计算结果与有限元结果对比。由图8可以发现，随锈蚀区域厚度减小，试件AF70X1000理论计算值与有限元模拟结果偏差有增大趋势，原因是随着锈蚀区域厚度减小，特征值屈曲分析结果呈整体-局部相关屈曲，有限元模拟结果偏小。由图8和图9可以发现，对于弹性弯曲屈曲应力，[σcry.preσcry.FSM]均值为1.027，标准差为0.019；对于弹性弯扭屈曲应力，[σcrxw.preσcrxw.FSM]均值为1.006，标准差为0.010，说明本文提出的计算方法可以用于计算锈蚀冷弯薄壁型钢柱整体屈曲应力。

4 结论

1） 随着锈蚀程度增大，弹性弯曲屈曲应力与弹性弯扭屈曲应力均逐渐下降，且下降速率有增大趋势。腹板锈蚀对弹性弯曲屈曲应力的影响大于弹性弯扭屈曲应力，而翼缘锈蚀对弹性弯曲屈曲应力与弹性弯扭屈曲应力的影响接近。

2） 弹性弯曲屈曲应力随锈蚀区域长度增大逐渐下降，且下降速率有减小趋势，而弹性弯扭屈曲应力随锈蚀区域长度增大近似线性下降。腹板锈蚀区域长度对弹性弯曲屈曲应力与弹性弯扭屈曲应力影响均大于翼缘锈蚀区域长度，而翼缘锈蚀区域长度对弹性弯曲屈曲应力的影响小于弹性弯扭屈曲应力。

3） 弹性弯曲屈曲应力与弹性弯扭屈曲应力随锈蚀区域宽度增大逐渐下降，且下降速率有增大趋势。腹板锈蚀区域宽度对弹性弯曲屈曲应力的影响大于翼缘锈蚀区域宽度，弹性弯扭屈曲应力随锈蚀区域宽度增大下降速率增大趋势大于弹性弯曲屈曲应力。

4） 理论计算值与有限元模拟结果吻合较好，本文提出的计算方法可以用于计算锈蚀冷弯薄壁型钢柱弹性整体屈曲应力。

参考文献：

[1]    赵金友. G550高强冷弯薄壁型钢受弯构件稳定性能与设计方法研究[M]. 哈尔滨：东北林业大学出版社，2018.

ZHAO J Y. Research on the stability performance and design method of G550 high-strength cold-formed thin-walled steel bending members[M]. Harbin： Northeast Forestry University Press， 2018

[2]    YE J， HAJIRASOULIHA I， BECQUE J， et al. Development of more efficient cold-formed steel channel sections in bending[J]. Thin-Walled Structures， 2016， 101（4）：1-13.

[3]    LEE J， KIM S M，PARK H S， et al. Optimum design of cold-formed steel channel beams using micro genetic algorithm[J]. Engineering Structures， 2005， 27（1）： 17-24.

[4]    ROSSI B，AFSHAN S，GARDNER L. Strength enhancements in cold-formed structural sections： Part Ⅰ[J]. Journal of Constructional Steel Research， 2013， 83： 177-188.

[5]    ROSSI B， AFSHAN S， GARDNER L. Strength enhancements in cold-formed structural sections： Part Ⅱ[J]. Journal of Constructional Steel Research，2013，83：189-196.

[6]    KYVELOU P， KYPRIANOU C， GARDNER L， et al. Challenges and solutions associated with the simulation and design of cold-formed steel structural systems[J]. Thin-Walled Structures， 2019， 141： 526-539.

[7]    李元齐， 徐厚军. 我国冷弯型钢结构发展现状及展望[J]. 建筑结构， 2019， 49（19）： 91-101.

LI Y Q， XU H J. Research and development of cold-formed steel structures in China[J]. Building Structure，2019， 49（19）： 91-101.

[8]    ZHANG J H， YOUNG B. Experimental investigation of cold-formed steel built-up closed section columns with web stiffeners[J]. Journal of Constructional Steel Research，2018， 147： 380-392.

[9]    谢清清， 邓年春. 轴偏转角对吊索腐蚀钢丝力学性能影响研究[J]. 华东交通大学学报， 2023， 40（4）： 103-111.

XIE Q Q， DENG N C. Effect of axis deflection angle on mechanical properties of corroded steel wire for slings[J]. Journal of East China Jiaotong University， 2023， 40（4）： 103-111.

[10]  ZHOU T， LI Y， REN L， et al. Research on the elastic buckling of composite webs in cold-formed steel back-to-back built-up columns： Part Ⅰ[J]. Structures， 2021， 30： 115-133.

[11]  ABBASI M， KHEZRI M， RASMUSSEN K J R， et al. Elastic buckling analysis of cold-formed steel built-up sections with discrete fasteners using the compound strip method[J]. Thin-Walled Structures， 2018， 124： 58-71.

[12]  ADANY S， SCHAFER B W. Buckling mode decomposition of single-branched open crosssection members via finite strip method[J]. Thin-Walled Structures， 2006， 44（5）： 563-584.

[13]  YU N， KIM B， YUAN W， et al. An analytical solution of distortional buckling resistance of cold-formed steel channel-section beams with web openings[J]. Thin-Walled Structures， 2019， 135： 446-452.

[14]  GATHEESHGAR P， POOLOGANATHAN K， GUNALAN S， et al. Elastic shear buckling of cold-formed steel channels with edge stiffened web holes[J]. Thin-Walled Structures， 2023，185：110551.

[15]  SELARRAJ S， MADHAVAN M. Design of cold-formed steel built-up columns subjected to local-global interactive buckling using direct strength method[J]. Thin-Walled Structures， 2021， 159： 107305.

[16]  TENG J G， YAO J， ZHAO Y. Distortional buckling of channel beam-columns[J]. Thin-Walled Structures. 2003，41（7）： 595-617.

[17]  MOEN C D， SCHAFER B W. Elastic buckling of thin plates with holes in compression or bending[J]. Thin-Walled Structures， 2009， 47（12）： 1597-1607.

[18]  MOEN C D， SCHAFER B W. Elastic buckling of cold-formed steel columns and beams with holes[J]. Engineering Structures， 2009， 31（12）： 2812-2824.

[19]  MOEN C D. Direct strength design of cold-formed steel members with perforations[D]. Washington： Johns Hopkins University， 2009.

[20]  姚永红. 腹板V形加劲冷弯薄壁卷边槽钢轴压柱稳定性能研究[D]. 哈尔滨： 哈尔滨工业大学， 2012.

YAO Y H. Research on the stability behavior of cold-formed thin-walled steel lipped channel columns with V-shaped stiffened web under axial compression[D]. Harbin：Harbin Institute of Technology， 2012.

[21]  姚永红， 王凤维. 开孔冷弯薄壁卷边槽钢柱弹性局部屈曲分析[J]. 建筑结构， 2015， 45（17）： 59-62.

YAO Y H， WANG F W. Elastic local buckling analysis of cold-formed thin-walled steel lipped channel column with holes[J]. Building Structure， 2015， 45（17）： 59-62.

[22]  SMITH F H， MOEN C D. Finite strip elastic buckling solutions for thin-walled metal columns with perforation patterns[J]. Thin-Walled Structures， 2014， 79： 187-201.

[23]  CASAFONT M， PASTPR M， BONADA J， et al. Linear buckling analysis of perforated steel storage rack columns with the finite strip method[J]. Thin-Walled Structures， 2012， 61： 71-85.

[24]  CASAFONT M， BONADA J， PASTPR M， et al. Linear buckling analysis of perforated cold-formed steel storage rack columns by means of the generalised beam theory[J]. International Journal of Structural Stability & Dynamics， 2018， 18（1）： 1850004.

[25]  NIE B， XU S， ZHANG Z， et al. Surface morphology characteristics and mechanical properties of corroded cold-formed steel channel sections[J]. Journal of Building Engineering， 2021（10）： 102786.