高动态场景下卫星通信信号的载波跟踪算法
张庆业 王力男

摘要:针对传统载波同步技术在低信噪比和大多普勒变化率条件下的载波跟踪失锁问题,文章提出一种高动态条件下载波跟踪算法,该算法对接收信号进行去调制后采用分段FFT算法估计多普勒频偏,把频率估计值作为测量值进行卡尔曼滤波完成噪声下的频率估计和跟踪。文章建立了仿真模型,对算法的跟踪性能及跟踪误差进行了仿真,仿真结果表明该算法能够在Es/N0=-1 dB的高动态条件下实现载波的估计和跟踪。
关键词:高动态;低信噪比;载波同步;卡尔曼滤波
中图分类号:TN929.5 文献标志码:A
0 引言
随着卫星技术的飞速发展,卫星移动通信系统具有覆盖范围广、不受地理条件限制、组网灵活、业务种类多样等优势[1]。低轨卫星星座相对于地面高速运动或者终端的高速运动,使收发双方处在高动态的通信条件下,造成通信信号严重的时间选择性衰落,在频域表现为信号大多普勒频移和高多普勒频率变化率。在低信噪比和高动态的通信条件下,传统的载波同步技术受限于载波环路带宽及宽带噪声影响,无法完成低信噪比下的同步。
针对高动态环境下载波跟踪问题,早期的高动态载波跟踪研究主要集中在高阶锁相环。20世纪80年代,JPL实验室Hurd等[2]研究得到最大似然估计(MLE)和扩展卡尔曼滤波(EKF)联合的捕获跟踪算法。该算法在信号概率分布基础上,根据最大似然准则得到接收信号似然函数,从而对信号的频率等参数进行估计。向洋[3]详细分析了高动态信号仿真生成方法,并针对高动态、低信噪比信号载波精确跟踪问题,提出了4种解决思路。本文开展了低信噪比和高动态的通信条件下的载波同步技术研究,对结合MLE和卡尔曼滤波的载波跟踪算法进行了仿真分析,研究结论可为工程应用提供参考。
1 载波同步技术
对接收信号进行载波频率估计,实际上是对接收信号去除调制信息后的载波残余频差进行估计。造成载波残余频差的原因有很多,其中最主要的是收发信机之间相对运动产生的多普勒频率偏移和频率源的频率差异。传统的载波残余频差的估计方法主要有4种,即基于周期图的最大似然频率估计、基于自相关函数的频率估计、基于相位差分求解的频率估计和锁频环(FLL)频率估计。前3种是开环频率估计方法,第4种是闭环频率估计方法。
高动态载波同步的研究主要有2类方法:基于FLL-PLL 的方法和基于卡尔曼滤波的方法。
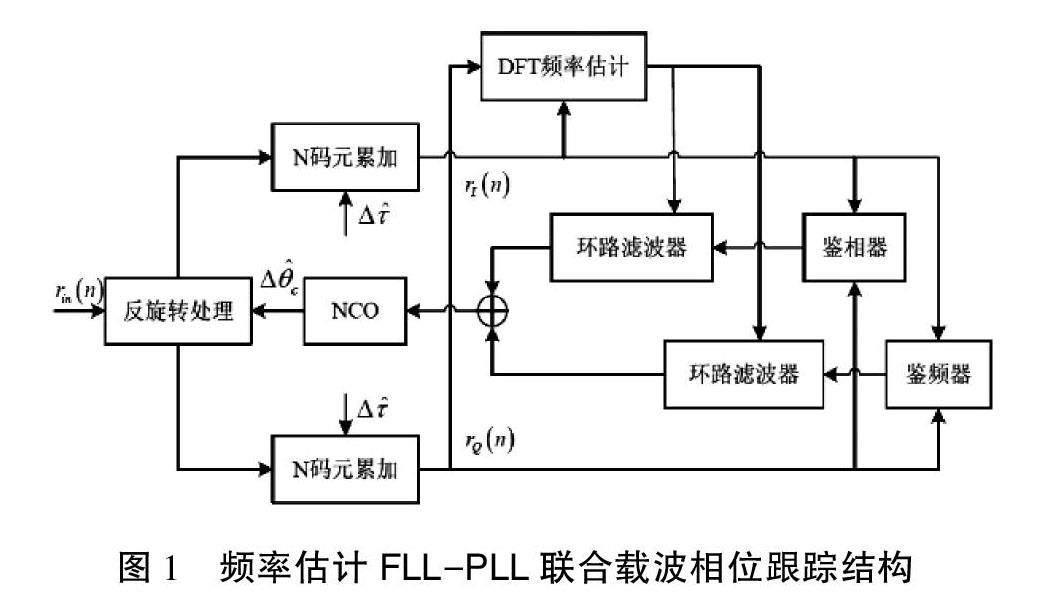
一种典型的DFT 频率估计辅助FLL-PLL 的联合载波相位跟踪结构如图1所示。需要说明的是,该结构中PLL环路没有采用噪声性能更优的判决反馈环而是采用Costas 环,这主要是考虑到增加环路与其他模块信号交互连接会带来更多不稳定因素。如果设计成熟,可以考虑使用判决反馈环代替Costas环。
卡尔曼滤波的核心是在处理含有噪声或偏差的信号时,结合其他估计值或测量值,可以得到更准确的观测值。基于卡尔曼滤波的载波跟踪环路原理如下。
该方法通过估计接收信号码元相位、频率和频率变化率等值,利用卡尔曼滤波递推方程对码元相位、频率和频率变化率等进行跟踪。
卡尔曼滤波模型公式如下:
xk=Axk-1+wk-1(1)
zk=Hxk+vk(2)
式中,状态变量参数xk为待估计信号的普勒频率及多普勒变化率,即xk=[f(k)s(k)]T。f(k)为信号的多普勒频率,s(k)为信号的多普勒频变化率。
状态转移矩阵为:
A=1T
01(3)
其中,T表示多普勒估计时间间隔。测量矩阵设置为H=[1 0],测量噪声的方差矩阵为R=σ2vI。
卡尔曼滤波更新过程如下。
预测过程的公式为:
x^-k=Ax^k-1(4)
P-k=APk-1AT+Q(5)
更新过程的3个公式如下:
Kk=P-kHTHP-kHT+R(6)
x^k=x^-k+Kk(zk-Hx^-k)(7)
Pk=(I-KkH)P-k(8)
式中,x^-k为对状态变量的先验估计,x^k为后验估计,Kk为卡尔曼滤波增益,P-k为先验估计误差的协方差矩阵,Pk为误差的协方差矩阵,Q为建模噪声的方差,R为测量噪声的方差。利用滤波结果f^1(k)及a^(k),预测下一段信号的频偏值,并调整下变频的NCO。
f2(k+1)=f^1(k)+a^(k)T(9)
FLL辅助PLL的方式在高动态环境下能够得到较好的跟踪效果。但是,增加FLL辅助会额外地增加总环路的跟踪误差,即FLL辅助PLL 的方式器相位跟踪误差会大于单独的锁相环路。与FLL辅助PLL的跟踪方式比较,基于卡尔曼滤波的载波相位估计门限信噪比低且噪声方差小,因此本项目算法选择基于卡尔曼滤波的跟踪方式。
2 基于FFT和卡尔曼滤波的载波同步算法
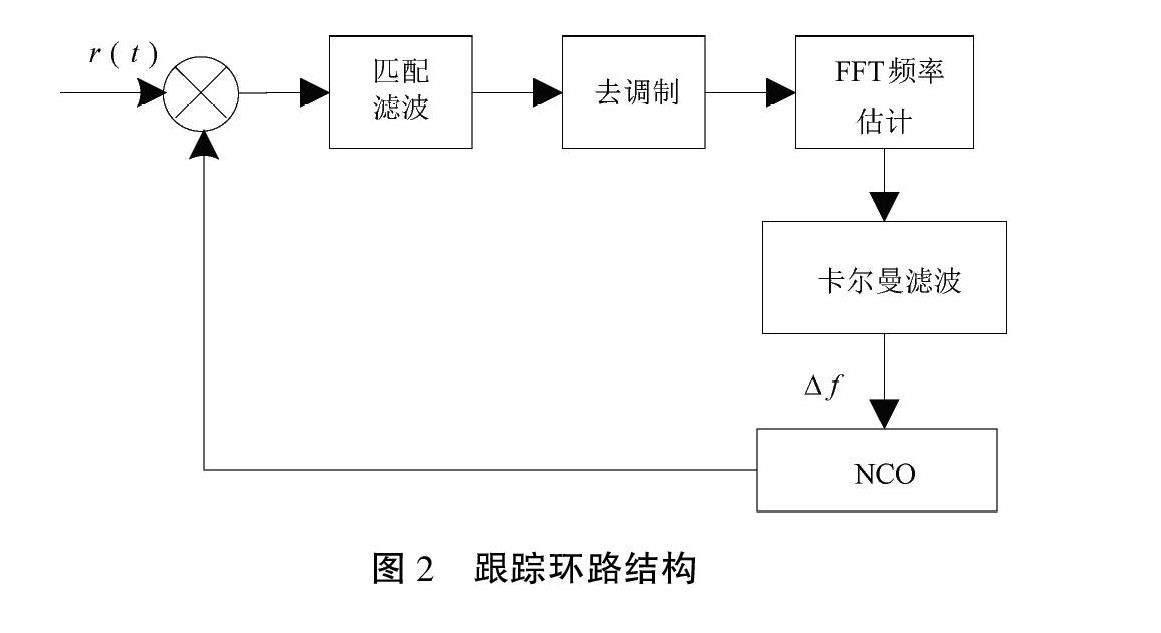
对频偏采用快速傅立叶变换 (Fast Fourier Transform,FFT)和卡尔曼滤波联合的估计算法;对介绍到的信号经过匹配滤波,去调制、FFT频率估计;并对频率估计结果进行卡尔曼滤波,滤波后的频率进入本地NCO调整,完成对接收载波的正确跟踪,具体如图2所示。
在噪声和初始状态为高斯独立分布的条件下,设接收信号为[4]:
y(mTs)=∑∞n=0angT(mTs-nT)ej[2π(f1+amTs)mTs+θ]+N(mTs)(10)
式中,an为输入调制符号,gT(·)为发射滤波器冲激响应,f1为接收信号频率,a为变化率,θ为相位,N(·)为噪声。该信号先经过接收滤波器匹配滤波,并对信号进行定时获得符号数据,进而对接收信号去调制后,对去调制后信号进行分段FFT估计其频率,每段长度为L,假设每段估计中由多普勒变化率引起的Δfl变化很小。为了低信噪比情况下保证估计性能,可利用FFT对此段信号进行频率估计:
Δf^k=12maxf{abs(FFT(r′k,l))}(11)
式中,r′k,l为去调制后第k个数据段待估计信号。去调制算法根据调制方式确定,BPSK采用平方去调制,QPSK信号采用四次方去调制。为了在大多普勒频率及大频率变化率下估计准确,频率估计所使用的信号段长度不能太长。
上述计算得到的频率值和变化率作为卡尔曼滤波的测量值,经过上节的更公式完成迭代更新,进而在低信噪比和高动场景条件下完成对多普勒频率及频率变化率的最佳估计。
3 算法仿真及结论
仿真的信号格式包括帧头同步序列和信息数据,其中同步序列长度为128个固定数据,用来完成初始频偏定位、位同步、相位估计、频率估计,如图3所示。
仿真的信道条件为AWGN信道,仿真采用BPSK调制,具体仿真参数如表1所示。
如图4所示,给出了在Es/N0=-1 dB下的频率跟踪曲线和频率估计误差曲线,由图看出频率估计误差在10 Hz以内。如图5所示,给出了Es/N0从 -3 dB到2 dB变化的频率误差均方根曲线,从图中看出随着信噪比的升高,误差逐渐减低,在-3 dB时频率误差均方根为5 Hz,能很好地满足跟踪需求。
4 结语
针对高动态环境下载波多普勒频偏变化率高的特点,本文研究低信噪比、大频率变化率条件下的载波跟踪问题。通过对频偏采用结合FFT和卡尔曼滤波的二级估计,经过FFT频率估计之后调整本地NCO,可以保证本地振荡频率对输入载波的正确跟踪,并建立仿真模型,对算法的跟踪性能及跟踪误差进行了仿真,仿真结果表明该算法能够在Es/N0=-1 dB的高动态条件下实现稳定载波跟踪。
参考文献
[1]庞江成,徐小涛,李超.卫星移动通信系统发展现状分析[J].数字通信世界,2020(1):144-147.
[2]HURD W J,STATMEN J I,VILNROTTIER V A,High dynamic GPS receiver using maximum likelihood estimation and frequency tracking[J].IEEE Transactions on Aerospace and Electronic Systems,1987(4):425-437.
[3]向洋.高动态GPS载波跟踪技术研究[D].武汉:华中科技大学,2010.
[4]田甜,安建平,薛斌,等.基于最大似然估计和Kalman滤波的BPSK载波同步方法[J].北京理工大学学报,2012(1):67-71.
(编辑 沈 强)
Carrier tracking algorithm for satellite communication signals in high dynamic scenarios
ZHANG Qingye, WANG Linan*
(The 54th Research Institute of CETC, Shijiazhuang 050081, China)
Abstract: A high dynamic condition carrier tracking algorithm is proposed to address the carrier tracking loss problem of traditional carrier synchronization technology under low signal-to-noise ratio and high Doppler rate conditions. This algorithm demodulates the received signal and uses a segmented FFT algorithm to estimate the Doppler frequency offset. The frequency estimation value is then used as a measurement for Kalman filtering to achieve frequency estimation and tracking in the presence of noise. A simulation model is established to simulate the tracking performance and tracking errors of the algorithm. Simulation results show that the algorithm can achieve carrier estimation and tracking under high dynamic conditions with Es/N0=-1 dB.
Key words: high dynamic; low signal-to-noise ratio; carrier tracking; Kalman filter

