把握“差倍问题”数量关系

孟莲

“差倍问题”是小学数学的重难点问题，贯穿学习的各个阶段。笔者认真研究了人教版数学三年级下册第4单元《两位数乘两位数》内容，以《口算乘法》课后习题“一个数乘10，得到的数比原来的数大72。原来的数是多少？”为例，谈谈如何引导学生在观察、分析、推理的过程中找出单位“1”的量，画出相应的线段图，并借助线段图分析数量关系，感悟差倍问题的解题方法。

一、创设情境，激发探究兴趣

有效的数学学习需要学生积极主动地参与数学活动，教师创设能吸引学生注意力、激发学生探究欲的问题情境，有助于学生自主、能动地展开学习。

为了激发学生探究差倍问题的兴趣，笔者课前设置悬念，让学生上学时每人带一把米。课堂上，笔者设置了如下教学情境。魔王抓走了国王和公主，需要智慧的你去解救。魔王出了如下两道题，答对一题就可以救出一人。问题1：“蚂蚁发现了一些米粒，它们召集所有蚂蚁往洞里搬米粒。A蚂蚁搬了一些米粒后扭伤了腰，在洞里休息。B蚂蚁搬了一些米粒后摔断了腿，也在洞里休息。所有蚂蚁搬完米粒后，发现B蚂蚁搬的米粒数量是A蚂蚁的10倍，B蚂蚁比A蚂蚁多搬了72粒米。A蚂蚁和B蚂蚁分别搬了多少粒米？”问题2：“C蚂蚁的力气最大，搬得最多，C蚂蚁搬的米粒数量是D蚂蚁的10倍，C蚂蚁比D蚂蚁多搬了360粒米。C蚂蚁和D蚂蚁分别搬了多少粒米？”学生被故事情境所吸引，阅读题目十分认真，并纷纷表示自己要救出国王和公主。于是，他们迫不及待地想要动手数米粒。

二、数学视角，分析数量关系

小学数学教学的重要目标是培养学生的数学思维，提高学生对数学知识的领悟力，以及运用数学知识解决实际问题的能力。笔者用如下方法引导学生用数学的眼光观察问题，用数学的思维思考问题。

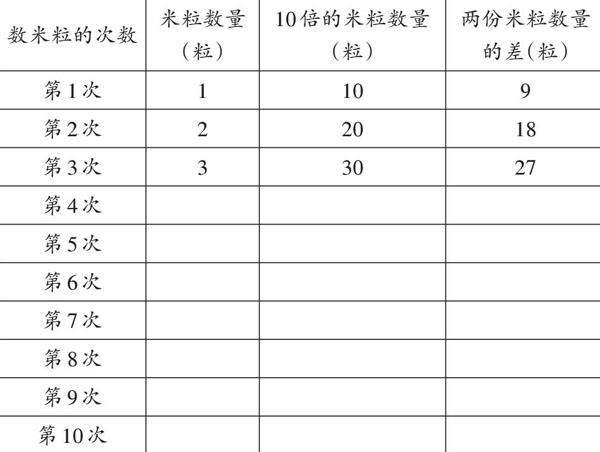
课堂上，为了避免学生盲目地数米粒，笔者先让他们思考怎样用数米粒的方法探究问题1。学生独立思考、小组交流后得出：B蚂蚁搬的米粒数量是A蚂蚁的10倍，如果A蚂蚁搬了1粒米，B蚂蚁就搬了10粒米，即B蚂蚁比A蚂蚁多搬了9粒米；如果A蚂蚁搬了2粒米，B蚂蚁就搬了20粒米，B蚂蚁比A蚂蚁多搬了18粒米；如果A蚂蚁搬了3粒米，B蚂蚁就搬了30粒米，B蚂蚁比A蚂蚁多搬了27粒米。学生认为，照这样列举，直到找到差值是72的两堆米，就能得出问题1的答案。笔者乘机提出活动要求：请同学们用这样的方式数米粒，一边数一边完成下面的表格。

学生先数1粒、1粒的10倍，接着数2粒、2粒的10倍，然后数3粒、3粒的10倍……一直数到10粒的10倍。

随后，笔者让学生观察表格，说一说有什么发现。有的学生发现：一个数的10倍就是这个数乘以10。有的学生发现：一个乘数不变，另一个乘数变大，积也变大。还有的学生发现：米粒数量是8时，米粒数量的10倍是80，80比8大72。至此，学生解决了第一个问题，得出A蚂蚁搬了8粒米，B蚂蚁搬了80粒米，B蚂蚁比A蚂蚁多搬了72粒米。学生解救了公主，很开心。

笔者趁热打铁，让学生用同样的方法解决问题2。有的学生开始数米粒，有的学生却提出质疑：C蚂蚁比D蚂蚁多搬了360粒米，这个数字太大了，如果一粒一粒地数，要数很长时间，还容易数错。这时，一名学生提出：观察前面数米粒的数据，我们可以发现一些规律，比如两份米粒数量的差都是9的倍数。笔者当即肯定了学生的发现，并让学生思考两份米粒数量的差是9的倍数的原因。通过观察和讨论，学生发现“10-1=9，20-2=18，30-3=27……100-10=90”，如果把第一份米粒的数量看成原数的1倍，第二份米粒的数量就是原数的10倍，两者的差就是原数的9倍，所以两份米粒数量的差一定是9的倍数。笔者引导学生总结，这个规律可以用“10倍数-1倍数=9倍数”表示，也可以写成“10倍数-1倍数=1倍数×9”，进一步归纳可以得出“1倍数=（10倍数-1倍数）÷9”。回归到题目，笔者引导学生这样分析：C蚂蚁搬的米粒数量是D蚂蚁的10倍，C蚂蚁比D蚂蚁多搬了360粒米，即C蚂蚁搬的米粒是“10倍数”，D蚂蚁搬的米粒是“1倍数”，它们的差360就是“1倍数”的9倍，所以，D蚂蚁搬的米粒数量可用“360÷（10-1）”计算，结果是40粒，进而得出C蚂蚁搬的米粒数是400粒。学生成功解答了这两道题，对差倍问题中的数量关系有了更清晰的认识。

三、数形结合，理解数量关系

解决问题的关键是理解数量关系。三年级学生受年龄和认知基础所限，往往很难直接理解抽象的数学知识，而画图作为一种有效的解题策略，能够直观地揭示数量关系。因此，教师在教学中培养学生运用数形结合思想画图解决问题的能力十分重要。

为了让学生直观地理解和分析问题，笔者引导：有没有更简洁的方法表示这些数量间的倍数关系呢？一名学生提出：可以用线段图表示倍数关系。学生尝试画线段图，小组交流画的过程和结果，并选出代表进行全班交流：问题1中B蚂蚁搬的米粒数量是A蚂蚁的10倍，从图1中可以直观地看出B蚂蚁搬的数量比A蚂蚁搬的数量多了9段线段，从题目可知B蚂蚁比A蚂蚁多搬了72粒米，也就是9段线段代表72粒米，由此可用72÷9算出每段线段代表的米粒数量即8粒，所以A蚂蚁搬了8粒米，B蚂蚁搬了80粒米。

由于有了第一次画图探究问题的实践经验，学生在分析问题2时自觉根据题意画出如下线段图（图2），并标注出“1倍数”“10倍数”等数据。

通过分析、交流，学生从图2中发现9段线段代表360粒，则每段线段代表40粒，即D蚂蚁搬了40粒，C蚂蚁搬了400粒。

为了让学生更好地掌握差倍问题的解题方法，笔者随即出示了一道变式题：被除数比除数大42，商是7，被除数和除数各是多少？这道题中没有直接出现倍数关系，只给出两个数的差，该如何解答呢？笔者给出提示：想想被除数、除数和商的关系，看看它们之间有没有隐藏的倍数关系。学生讨论后得出：被除数÷除数=7，即被除数=除数×7，这说明被除数是除数的7倍，根据题意，可以把除数看成“1倍数”，用1段线段表示，被除数则可用7段线段表示，根据被除数比除数大42，可以画出如下线段图（图3）。[除数：

根据线段图，学生可以直观地看出42代表6段线段，可用“42÷6=7”得出每段线段代表7，即除数是7，则被除数是49。

学生在画线段图的过程中深刻地理解了题目中隐含的两个数量间的倍数关系，将其转化成熟悉的简单的差倍问题，增强了解决实际问题的能力。

（作者单位：黄冈市红安县竹林实验学校）

责任编辑  张敏