基于变形监测成果的基坑支护设计稳定性评价

收稿日期：2023-10-20；修回日期：2023-12-19

作者简介：李锐豪（1990- ），男，本科，工程师，主要从事地质工程工作。E-mail：1377604277@qq.com

引用格式：李锐豪，2024.基于变形监测成果的基坑支护设计稳定性评价［J］.城市地质，19（2）：225-232

摘 要：采用粒子群算法、广义回归神经网络和差分自回归移动平均模型实现基坑变形预测，评价基坑施工过程中的稳定性，以佐证基坑支护措施的有效性。基坑区地质条件、近接条件均较为复杂，需采用刚度大的支护结构来控制基坑变形，因此，将基坑支护形式确定为桩锚支护结构，且为确保基坑支护体系的经济性，还进行了分区支护措施设计。在基坑稳定性评价过程中，现阶段条件下的沉降变形的变化范围为12.68～21.42 mm，均值为17.84 mm，水平位移的变化范围为15.08～22.49 mm，均值为18.68 mm，得出两类变形均小于变形控制值，说明基坑目前的变形在变形控制值范围内，其稳定性较好；通过变形预测，得出基坑后续变形具收敛趋势，后续的变形值范围为21.35～23.58 mm，也小于变形控制值，说明基坑后续的变形控制也较好，基坑稳定性较优。

关键词：基坑；支护设计；变形监测；广义回归神经网络；变形预测

Design and stability evaluation of foundation pit support based on deformation monitoring results

LI Ruihao

（Henan No.2 Institute of Geological and Mineral Resources Survey Co.， Ltd.， Zhengzhou 450000， Henan， China）

Abstract： Particle swarm optimization algorithm， generalized regression neural network， and differential autoregressive moving average model are used to predict the deformation of foundation pits. The stability of the foundation pit construction process is evaluated based on the prediction results to demonstrate the effectiveness of foundation pit support measures. The geological conditions and proximity conditions in the target excavation area are relatively complex， requiring the use of rigid support structures to control the deformation of the foundation pit. Therefore， pile anchor support structure is chosen as the form of foundation pit support. To ensure the economic efficiency of the foundation pit support system， zoning support measures are also designed. In the process of evaluating the stability of the foundation pits， the range of settlement deformation under current conditions is 12.68-21.42 mm， with an average of 17.84 mm. The range of horizontal displacement change is 15.08-22.49 mm， with an average of 18.68 mm. It is found that both types of deformation are smaller than the deformation control value， indicating that the current deformation of the foundation pit is within the deformation control value range and has good stability. Through deformation prediction， it is found that the subsequent deformation of the foundation pit has a convergence trend， and the range of subsequent deformation values is 21.35-23.58 mm， which is also smaller than the deformation control value. This indicates that the subsequent deformation control of the foundation pit is also good， and so is the stability of the foundation pit.

Keywords： foundation pit; support design; deformation monitoring; generalized regression neural network; deformation prediction

随着城市建设的快速发展，城市基坑工程数量越来越多，受近接条件限制，变形控制越来越重要（穆海旺等，2022；王长青等，2022；赵蕊等，2023）。目前，有不少学者开展了基坑支护设计的相关研究，如孔跃跃等（2023）开展了基坑结构的非对称设计，李连祥等（2023）进行了非饱和土区的基坑支护设计研究，黄俊光等（2022）分析了超大深基坑群的支护设计方案，陈林靖等（2023）采用强度折减法分析了坑中坑基坑内外坑相互影响规律及其破坏形式。上述研究成果显示开展基坑支护设计研究是十分必要的，但限于基坑所处地质条件差异，有必要结合工程实际开展针对性的基坑支护设计研究。

为进一步确保基坑施工过程中的稳定性，在基坑支护设计后，提出以变形监测成果为基础，开展基坑变形控制效果评价，且将该分析过程划分为两步，其一，对比基坑现有变形量与变形控制值，评价基坑现有状态的变形控制效果；其二，利用变形预测思路开展基坑后续变形研究，通过变形预测结果来评价基坑后续变形控制效果。为实现基坑稳定性合理评价，重点需构建基坑变形预测模型，广义回归神经网络具有较强的非线性特征（苗兰弟等，2021），可以作为基坑变形预测模型的基础。

本文采用粒子群算法、广义回归神经网络和差分自回归移动平均模型实现基坑变形预测，并以预测结果评价基坑施工过程中的稳定性，以佐证基坑支护措施的有效性，以期为类似工程积累经验。

1  工程概况

项目属房屋住宅建筑工程项目，位于河南省焦作市，总计包括5栋建筑，其中，2栋层数为24层，3栋层数为18层，地下层数为2层。

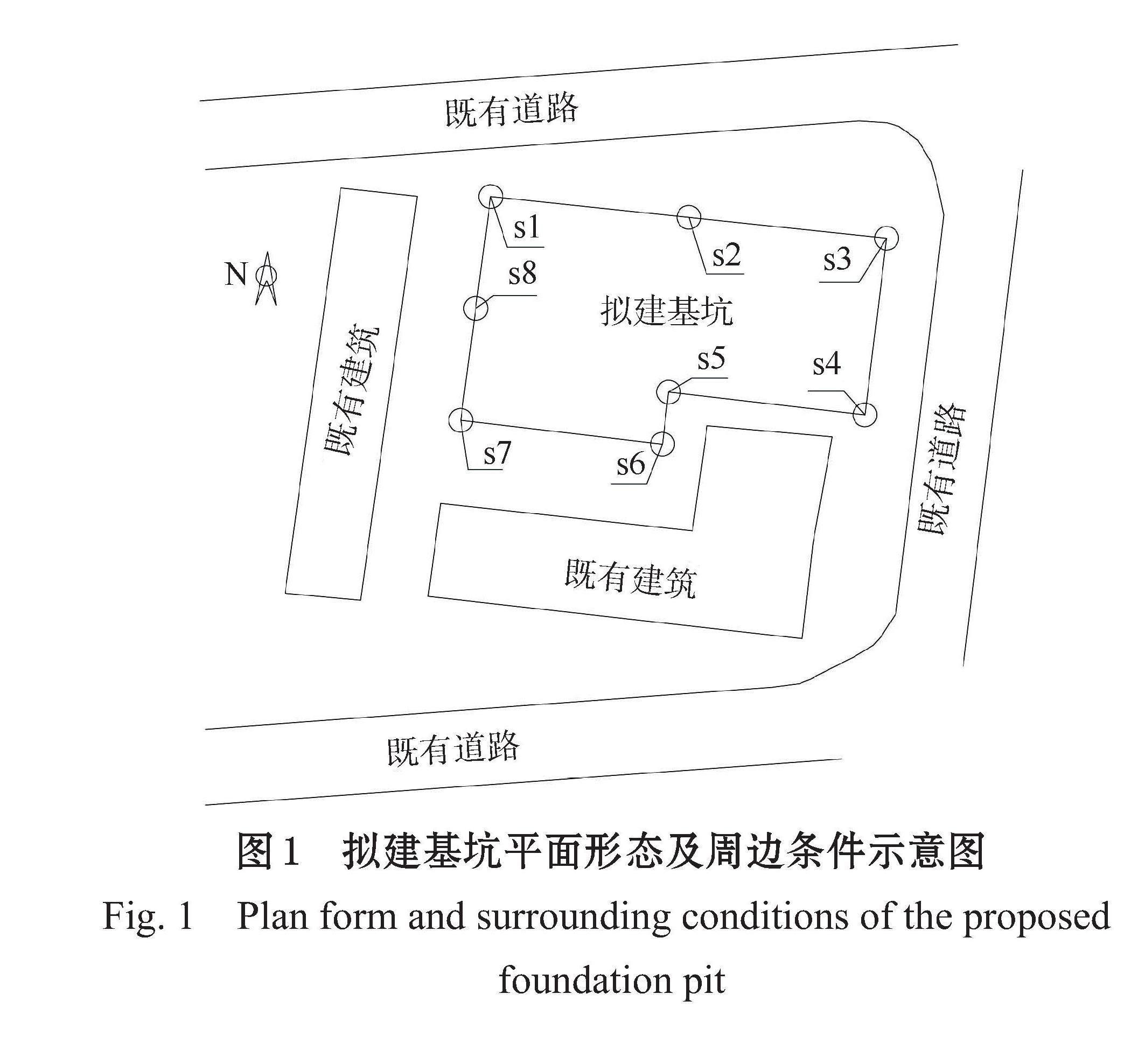
拟建基坑面积约8 483.28 m2，平面形态近似呈矩形（图1），开挖深度大于5.0 m，属深基坑。

项目区属河漫滩地貌，高程范围34.2～37.2 m，高差相对很小，整体地形很平坦；区内岩土层自上而下为杂填土、粉质黏土、含碎石黏土、卵石，其基本特征如下：

①杂填土。颜色杂乱，多由建渣、黏性土组成，硬质含量多大于50%，稍湿、松散，厚度分布不均，一般1.1～3.0 m。

②粉质黏土。黑、灰色，湿，可塑—软塑，广泛分布于场区，局部夹杂少量砾石，含量少于7%，分布厚度2.9～4.4 m。

③含碎石黏土。黄褐色，稍湿，可塑，碎石含量18%～32%，母岩多为石英岩，磨圆度差，呈次棱角状，分布厚度4.3～5.8 m。

④稍密卵石。灰黄色、灰色，稍密，饱和，卵石含量55%～60%，孔隙由黏性土充填，磨圆度较好，卵石成分由花岗岩、石英岩组成，分布厚度6.1～8.8 m。

⑤中密卵石。灰黄色、灰色，中密，饱和，卵石含量60%～65%，磨圆度也较好，卵石成分由花岗岩、石英岩组成，揭露厚度大于10.2 m。

通过试验及经验成果统计，得到各类地层的基本特征参数如表1所示。

项目区地表水不发育，地下水多以上层滞水、潜水形式存在；第4层、5层的岩性主要为卵石，含水层渗透系数大、富水性好，易对土体工程性质产生较大影响。

基坑周边近接条件较为复杂，其中，北侧、东侧均是近接既有道路，最小净距13.2～16.0 m；西侧、南侧均是近接既有建筑，最小净距10.5～18.2 m，其基础均是桩基础。

在基坑变形监测过程中，沉降变形、水平位移监测是十分重要的，因此，后续重点以此两类变形进行示例性分析，且在此两类项目变形监测过程中，监测频率为一天一次，监测仪器采用全站仪及电子水准仪，监测精度为1.0 mm。

2  基坑支护设计

在基坑开挖范围内，开挖地层主要为粉质黏土层、卵石层，需严格控制基坑施工流程，确保项目质量，基坑周边近接建筑物较为复杂，且净距较小，因此，采用刚度大的支护结构能有效控制变形，尽可能减小基坑施工对周边既有建筑物的影响。

2.1  支护设计方案

基坑支护形式为桩锚支护结构，考虑基坑周边近接条件的差异性，采用分区支护设计。以图1中s1～s8监测点进行支护分区划分，其中，支护Ⅰ区的范围为s1-s2-s3-s4，支护Ⅱ区的范围为s4-s5-s6，支护Ⅲ区的范围为s6-s7-s8-s1。各区支护方案设计见表2。

基坑支护措施示意图见图2。

2.2  支护设计参数

1）桩间锚喷的设计参数。在基坑开挖基面、桩间面上，先挂22#钢板网，且为保证后续喷射混凝土的效果，于基面与钢板网间设置垫块，垫起距离不小于2 cm；当完成挂网后，开展混凝土喷射处理，混凝土等级为C20，细石∶中砂∶水泥=2∶2∶1。

2）支护桩的设计参数。将支护桩的桩顶设计于地面，桩径均设计为800 mm，混凝土强度为C30，其他设计参数见表3。

3）冠梁的设计参数。冠梁设计尺寸为0.8 m ×1.0 m，主筋按8根直径22 mm和3根直径16 mm进行配筋，箍筋直径为8 mm，间距为20 cm，混凝土等级为C30。

4）锚杆的设计参数。锚杆设计长度均为22 m，直径为13 cm，其他设计参数见表4。

2.3  施工技术分析

1）支护桩的施工技术

支护桩的施工工艺流程：先开展场地平整、测量定位，其后埋设护筒，将钻机移至对应位置处开展钻孔工作，且在此过程中应进行点位复核；在钻机钻进过程中，采用泥浆护壁，确保周围土体稳定，并当达到设计高程后，再进行提钻、清孔工作；对完成后的钻孔进行质量检查，若满足要求，则放钢筋笼、浇筑混凝土。

2）锚杆的施工技术

锚杆的施工工艺流程：先对基面进行整理，并进行放点；当钻机到位后，对锚杆位置进行复核，其后再进行钻孔，直至设计深度；完成钻孔后，先安装锚杆杆体及进行混凝土灌注；当达到设计强度后，根据设计要求，对锚杆进行张拉、锁定。

3  基坑稳定性评价

3.1  评价方法

3.1.1  评价方法的总体设计

在基坑变形监测过程中，均会设置相应的控制值，若基坑变形均在控制范围内，说明基坑稳定性较好；反之，基坑稳定性较差。结合上述，将基坑稳定性评价思路设计为两步。第一步：将基坑现有变形量与变形控制值对比，前者更小，说明基坑目前的变形在变形控制值范围内，其稳定性较好。第二步：利用变形预测思路开展基坑后续变形研究，若其后续变形趋于稳定且预测变形量仍在变形控制值范围内，说明基坑后续的变形控制也较好，基坑稳定性也较优。

3.1.2  变形预测模型构建

根据上述，在评价思路第二步中开展基坑变形预测思路的构建。结合以往研究成果（马琳，2023；钟国强等，2019；李晓斌等，2023；宁永香等，2023；段青达等，2020），广义回归神经网络（Generalized Regression Neural Network，GRNN）具有较快的训练速度及较强的映射能力，因此，提出以其作为基坑变形预测模型的基础方法。GRNN具4层拓扑结构，相应名称及映射关系见图3。

结合GRNN的拓扑结构，将各层作用如下：

①输入层。先对基坑变形数据进行整理，尤其剔除歧义数据，再利用此层将基坑变形输入信息传递至模型结构中。

②模式层。当收到输入信息后，此层重点利用激励函数进行其映射处理，且为确保映射效果，此层与输入层的节点间不能出现混乱现象，并将其映射公式表示为：

（1）

式中，hi为模式层的映射值，xi为对应期望值，m为基坑变形的输入信息，S为光滑因子。

③求和层。在模式层信息映射处理基础上，此层再进一步增加节点维度，对hi值进行持续信息变换，相应求和参数A和变化参数G j的公式为：

（2）

（3）

式中，q为求和层的维度值，kij为求和层的训练参量。

④输出层。经过求和层进一步的信息变换处理，此层再对其处理后的信息进行整合，即可输出变形预测值，公式为：

（4）

式中，zj为GRNN的基坑变形预测结果。

值得指出的是，使用经验（李伟等，2023；蔡群群，2023；袁志明等，2021）显示光滑因子S的随机性强，会对预测结果的稳健性造成影响，因此，提出利用粒子群算法（Particle Swarm Optimization，PSO）开展光滑因子S的寻优处理。在PSO的寻优过程中，具体步骤为：

①初始化粒子种群，即将粒子个数设计为200个，最大寻优更新次数为450次，2个学习因子为1.5和2.0等。

②将预测误差作为适应度函数，计算所有粒子的适应度值，并通过对比，确定全局初步最优值。

③按照学习因子，调整粒子速度、位置参数，并对调整后的粒子适应度值进行重新计算，将其计算值与全局最优值进行对比，以实现全局最优值的筛选处理。

④当达到终止学习条件后，将全局最优值对应的光滑因子S输出，即可完成PSO对GRNN的寻优处理。

PSO对GRNN的寻优流程如图4所示。

根据前述，将基坑变形预测模型确定为PSO-GRNN，但限于基坑变形的非线性特征，PSO-GRNN对其预测结果会存在一定影响；为确保预测精度，提出通过差分自回归移动平均模型（Autoregressive integrated moving average model，Arima）开展PSO-GRNN预测误差的修正补充预测（牛全福等，2022），并将其训练函数公式表示为：

（5）

式中，Rt为预测误差的修正补充预测值，φm为自回归变量，p、q为回归变量，rt-m为PSO-GRNN的预测误差值，at-j、at为白噪声，θj为滑动因子。

通过上述，基坑变形预测模型最终为PSO- GRNN-Arima；为合理评价预测效果，先构建相对误差指标Xt：

（6）

式中，Yt为变形监测值，Kt为变形预测值。

再以指标为基础，求解其均值Mr和方差值Var 。前者主要用于评价预测精度，其值越小，说明预测精度越高；后者主要用于评价预测过程的稳定性，其值越小，说明预测过程越稳定。

3.2  评价结果

筛选8个监测点，按照2天1次的监测频率，共计统计得到33期监测成果，其沉降变形、水平位移监测结果见表5。沉降变形（监测点编号为sc1～sc8）的变化范围为12.68～21.42 mm，均值为17.84 mm；水平位移（监测点编号为ss1～ss8）的变化范围为15.08～22.49 mm，均值为18.68 mm；通过对比，水平位移的变形值略大于沉降变形的变形值，且不论沉降变形，还是水平位移，所有监测的变形值均小于变形控制值（30 mm），说明基坑目前的变形在变形控制值范围内，其稳定性较好。

在沉降变形、水平位移中分别选取2个变形值最大的监测点进行预测分析，即沉降变形选取sc3和sc7，水平位移选取ss5和ss6。其变形监测成果见表6。从表6可看出，4个监测点的变形值具有持续增加特征。

为验证PSO-GRNN-Arima构建过程的合理性，以sc3号监测点为例，对比不同构建过程阶段的预测效果，结果见表7。据表7，在第29～33期的验证预测结果中，从GRNN→PSO-GRNN→PSO-GRNN-Arima的Xt均具有不同程度的减小特征，经统计，GRNN的Mr值为3.31%，Var值为0.057；PSO-GRNN的Mr值为2.75%，Var值为0.008；PSO-GRNN-Arima的Mr值为2.03%，Var值为0.003。因此，这些数据表明，随预测模型的递进构建，预测精度及稳定性均呈逐步提高趋势，验证了PSO-GRNN-Arima构建过程的合理性。

其次，再以PSO-GRNN-Arima开展其他监测点的变形预测和外推预测，所得结果见表8。据表8，sc3的Mr值为2.03%，Var值为0.003；sc7的Mr值为2.10%，Var值为0.008；ss5的Mr值为2.08%，Var值为0.011；ss6的Mr值为2.14%，Var值为0.004。根据4个监测点的预测结果，其Mr值相当且较小，Var值亦不大，此结果充分验证了PSO-GRNN-Arima在基坑变形预测中的适用性。

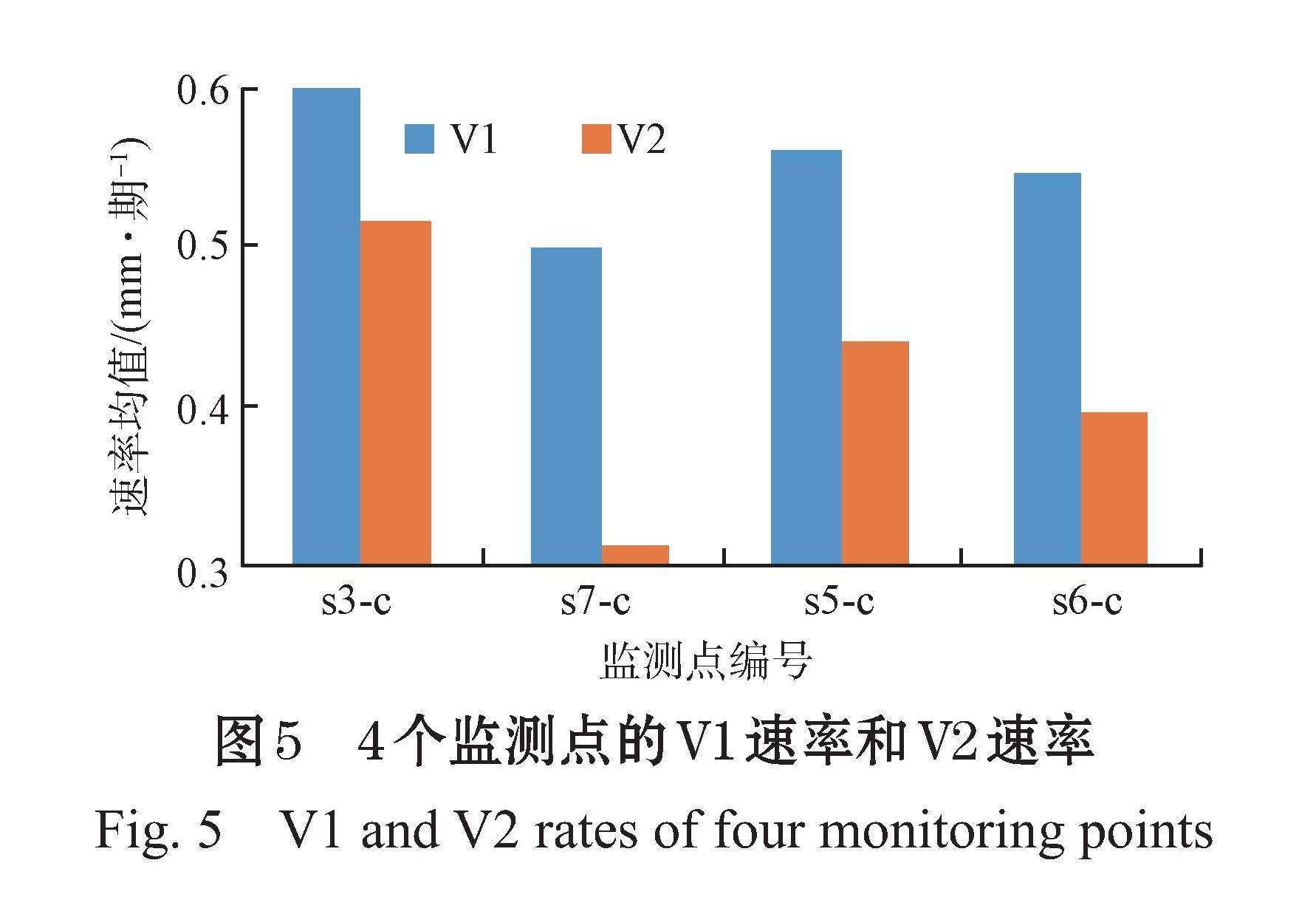
据表8中34～37期的外推预测结果，得到相应累计变形量均会一定程度增加，并构建两类速率特征参数来衡量相应变形的后续发展趋势，即V1速率（30～33期的变形速率均值）和V2速率（34～37期的变形速率均值），若V1速率更大，说明基坑变形具收敛趋势；反之，说明基坑变形具加速增加趋势。

经统计，得到4个监测点的V1速率和V2速率结果见图5。据图5，4个监测点的V2速率均不同程度地小于V1速率，降低幅度依次为20.07、37.40、21.37和27.43%，尤其以sc7的下降幅度更大，说明4个监测点的变形均收敛趋势。

通过外推预测，得到4个监测点后续的变形值范围为21.35～23.58 mm，也小于变形控制值，说明基坑后续的变形控制也较好，基坑稳定性也较优。

综合上述，不论目前还是以后，基坑变形均在变形控制值范围内，说明基坑稳定性较好。

4  结论

通过变形监测成果基础上的基坑支护设计稳定性评价，得到以下结论：

1）根据工程实际条件，将桩锚支护结构作为基坑支护形式，并结合基坑周边近接条件进行分区支护措施设计是合理的。

2）结合变形监测成果，监测时段内的沉降变形、水平位移变形值均小于变形控制值（30 mm），说明基坑目前的变形在变形控制值范围内，其稳定性较好。

3）通过PSO-GRNN-Arima的变形预测，得出该模型适用于基坑变形预测，具有较高的预测精度，可以推广应用，以进一步佐证该模型的普适性。

4）基坑后续变形具收敛趋势，且预测得到的变形值也小于变形控制值，说明基坑后续的变形控制及稳定性较好。

参考文献

蔡群群， 2023.基于粒子群算法改进支持向量机的深基坑变形预测研究［J］. 黑龙江交通科技， 46 （5）： 97-99.

陈林靖， 孙瑞轩， 罗一鸣， 2023.基于强度折减法的坑中坑整体稳定性数值模拟分析［J］.城市地质， 18（3）：67-75.

段青达， 陈天伟， 田立佳， 郑旭东， 陈明， 2021.基于改进型ARIMA-GRNN模型的高边坡变形预测［J］. 桂林理工大学学报， 41 （2）： 342-349.

黄俊光， 李健斌， 王伟江， 罗永健， 2022.系列超深超大基坑群设计实践与探索［J］.地下空间与工程学报， 18（4）：1 317-1 327.

孔跃跃， 万琪伟， 丁海滨， 周悦龙， 黄展军， 徐长节， 2023.非对称开挖双支撑支护结构优化设计研究［J］.隧道建设（中英文）， 43（S1）：356-364.

李连祥， 李红波， 韩刚， 郭龙德， 赵仕磊， 2023.济南非饱和土基坑支护设计［J］.山东大学学报（工学版）， 53（3）：41-49.

李伟， 邓乐平， 2023.基于BP神经网络模型的基坑变形监测分析研究［J］. 测绘与空间地理信息， 46 （7）： 140-143.

李晓斌， 白海军， 2023.高位远程古滑坡既有变形特征和后续变形发展规律研究［J］. 大地测量与地球动力学， 43 （11）： 1 129-1 135.

马琳， 2023.基于ICEEMD-ICA准则进行数据处理的基坑变形组合预测研究［J］.地质与勘探， 59（5）：1 074-1 082.

苗兰弟， 任庆国， 2021.考虑随机误差的软土基坑沉降趋势分析及预测［J］.中国安全生产科学技术， 17（6）：111-116.

穆海旺， 张训玉， 文萌， 刘静， 曹磊， 徐磊， 2022.桩锚支护体系在基坑工程中的应用［J］.城市地质， 17（2）：240-248.

宁永香， 崔希民， 崔建国， 2023. 基于ABC-GRNN组合模型的露天矿边坡变形预测 ［J］. 煤田地质与勘探， 51 （3）： 65-72.

牛全福， 李月锋， 张曼， 傅建凯， 马亚娜， 2022.基于Kalman滤波的ARIMA-NAR神经网络模型在深基坑沉降监测中的应用［J］.兰州理工大学学报， 48（2）：131-135.

王长青， 王坦， 熊育久， 2022.长春地铁站深基坑支护设计方案对比研究［J］.城市地质， 17（2）：232-239.

袁志明， 李沛鸿， 刘小生， 2021.顾及邻近点的改进PSO-SVM模型在基坑沉降预测的应用研究［J］. 大地测量与地球动力学， 41 （3）： 313-318.

赵蕊， 邓飞， 魏燃， 李小林， 付宏岐， 2023.南宁地铁基坑围护结构变形监测分析及应用［J］.矿产勘查， 14（9）：1 713-1 721.

钟国强， 王浩， 李莉， 王成汤， 谢壁婷， 2019.基于SFLA-GRNN模型的基坑地表最大沉降预测［J］.岩土力学， 40（2）：792-798.