基于哈达玛矩阵的改进部分传输序列算法

郭伟 刘浩

摘要：部分传输序列（Partial Transmit Sequences，PTS）是一种常用的降低正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）系统峰均功率比（Peak-to-Average Power Ratio，PAPR）的方法，其能确保不给系统带来信号畸变。PTS算法的遍历特点导致计算复杂度大幅提高，文章提出的基于哈达玛矩阵的改进PTS算法将在很大程度上保障信号PAPR的性能，降低计算的复杂度。

关键词：正交频分复用；峰均功率比；部分传输序列

中图分类号：TN929文献标志码：A

0 引言

正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）技术被广泛地应用于无线通信领域^[1]。然而，由于系统的叠加，所出现的较高峰均功率比（Peak-to-Average Power Ratio，PAPR）将使信号失真，提高了信号的误码率。因此，PAPR问题已经成为OFDM技术实用化的一大障碍^[2]。

对于一个包含N个子载波的OFDM系统，在一个符号时间间隔内，其基带离散时间信号可表示为：

其中，X_k（k=0，1，…，N-1）是由信号经调制后得到的频域信号，x_n是经OFDM调制后信号，n是离散的时间点。系统在实现功能时，由于信号的相互叠加，导致较大的PAPR。本文提出的基于哈达玛矩阵的改进PTS算法将在很大程度上保障信号PAPR的性能，降低了计算的复杂度。

1 传统PTS算法存在的问题

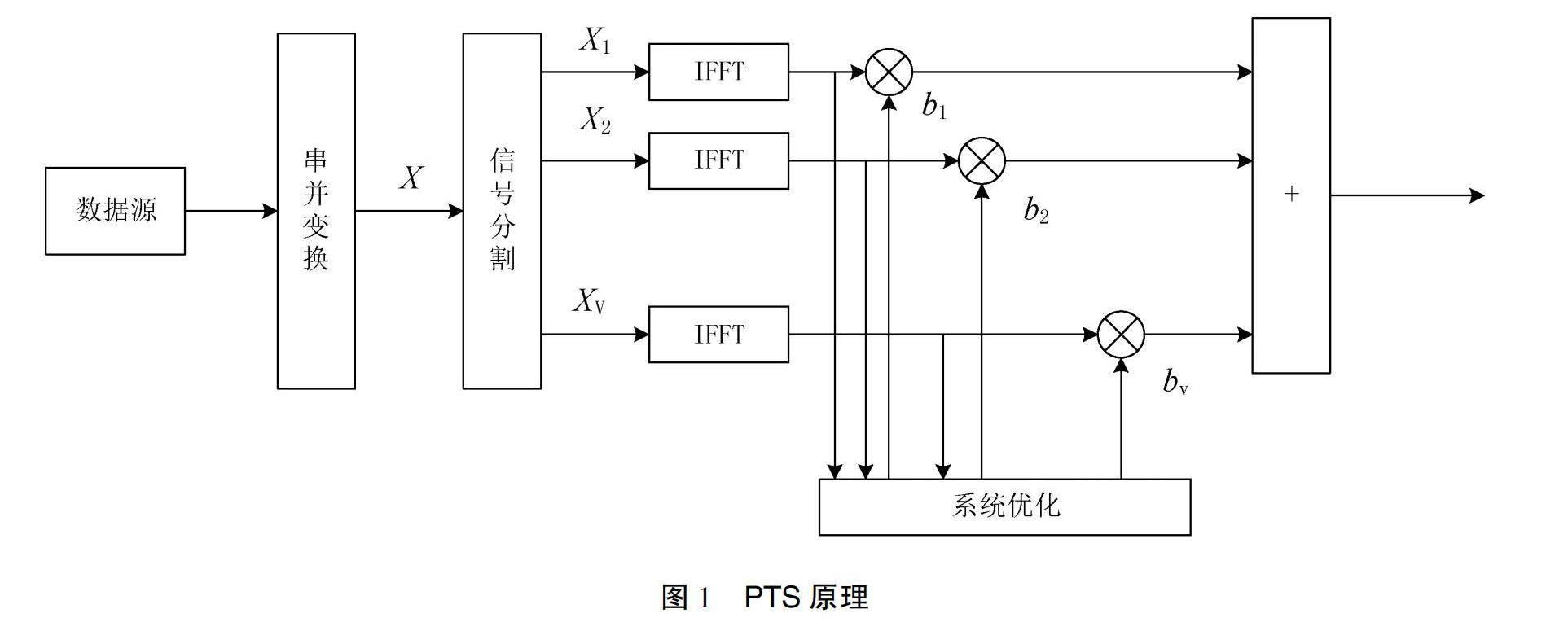
目前，在常用的有效降低信号PAPR的方法中，部分传输序列（Partial Transmission Sequence，PTS）是最常用且有效的方法，但其应用会增加系统的复杂度。PTS原理如图1所示。

首先，OFDM系统对信号进行分割后，进行快速傅里叶逆变换（Inverse Fast Fourier Transform，IFFT）。然后，信号与系统优化相位因子序列合并。最后，对每种组合进行遍历后，计算和选择信号PAPR。

以上述实现过程为例，对于传统PTS算法，其总计需要完成：W^V-1次系统优化与分割信号的乘法运算；W^V-1次V分割信号的加法运算；W^V-1次筛选排序；将以上计算复杂度设置为基准单位C=W^V-1。由此可得结论：分块数V和相位因子取值个数W中任意一个增加，都会给传统PTS算法的计算复杂度带来指数型增长。

2 改进原理及实现步骤

2.1 原理1

考虑到系统优化的遍历与最原始的数据有较大关联，结合哈达玛矩阵的特性^[3]，即任意2行都是不相关且正交的，原理如下所述。

最低阶的哈达玛矩阵为：

其中，N=2^m，U为直积。根据矩阵特点，改变矩阵中的任意数据，不会影响整体的正交性质。

2.2 原理2

传统的PTS算法是在整个过程中遍历全部可能取得的最优解，导致算法具有较大的计算复杂度^[4-5]。对于传统的迭代线性搜索算法，实现过程如下：首先，系统随机确定一个点；然后，在该点的附近不断计算更优解；最后，确定算法的极值^[6]。

以图2所示搜索最大值的方法找到算法极值，具体实现方法为：首先，在曲线上选定一点；然后，用比较算法不断计算附近区域的更大值；最后，确定曲线的极大值点。显然，随机初始化点的选择对极大值的选定至关重要。例如：设点E为初始化点，在对比附近极大值的过程中，迭代线性搜索算法最终确认的极大值点为点F，点F显然不是曲线的最大点。

传统的PTS遍历搜索算法过程相当于在二维空间中寻找最大值点H的过程。迭代移位线性搜索算法初始化相位因子就相当于在整条曲线上随机选取一点，然后，用搜索算法找到该点附近的极大值点。

2.3 改进算法的实现原理和步骤

改进算法流程如图3所示。在信号处理前，首先，对系统优化因子进行哈达玛矩阵处理，处理完成后的每行矩阵系统优化因子均不相关且正交；然后，采用加工后的系统优化因子对分割信号进行合并优化，以实现最小PAPR的1组数据作为初始值，记录该组最小PAPR的优化后相位因子，将其作为传统迭代算法的1组原始系统优化因子；最后，不断优化迭代线性搜索算法，随着迭代次数的增加，系统PAPR性能趋向于传统的PTS算法^[7]。由于哈达玛矩阵的特性，系统优化因子具有更好的正交特性，极大地优化了初始位置的选择，从而减少了系统优化因子的遍历过程，大幅降低了计算的复杂度。

3 计算复杂度分析

基于上述分析，在最优解算法的实现过程中主要完成如下运算：W×V×n次系统优化与分割信号的乘法运算；W×V×n次V分割信号的加法运算；W×V×n次选择操作。在本算法中，哈达玛矩阵对系统优化因子进行筛选的过程可用于产生原始系统的优化因子，根据初始系统优化因子的组数进行m次迭代，以实现最优的解。因此，改进算法的计算复杂度为C_PTS-MISLS-H=C_MISLS=m×W×V×n。

综上所述，改进算法的计算复杂度与原始算法的系统优化因子组数成正比；相对于传统算法，改进算法的计算复杂度C=W^V-1大幅降低。

4 性能分析

传统PTS和本文提出的改进PTS算法的PAPR性能对比如图4所示。

由图可知，在分组数相同的情况下，本文提出的改进算法通过哈达玛矩阵对系统优化因子的初始化进行筛选，结合不同迭代优化，以实现最优的PAPR性能；同时，在实现过程中，根据初始系统优化因子的组数进行m次迭代，改进算法的计算复杂度与原始算法的系统优化因子组数成正比；相较于传统PTS算法的复杂度呈指数型增加，改进算法的计算复杂度随V值变化不明显。

5 结语

在矩阵的改进系统优化因子的基础上，本文提出的改进算法通过系统迭代优化实现最优PAPR性能。与传统PTS算法相比，本文提出的改进算法既能提高PAPR计算性能，又能降低系统计算复杂度。

参考文献

[1]YANG H W. A road to future broadband wireless access： MIMO-OFDM based air interface[J]. IEEE Communications Magazine， 2005（1）： 53-60.

[2]SAMIR B. New Technologies of Information and Communication（NTIC）：A PAPR Reduction for STBC MIMO-OFDM Systems in 4G Wireless Communications Using PTS Scheme，November 8–9，2015[C]. Mila：IEEE，2015.

[3]JIANG T，WU Y. An overview peak-to-average power ratio reduction techniques for OFDM signals[J]. IEEE Transactions on Broadcasting， 2008（2）： 257-268.

[4]WANG Y C， LUO Z Q. Optimized iterative clipping and filtering for PAPR reduction of OFDM signals [J]. IEEE Transactions on Communications， 2011（1）： 33-37.

[5]TONG J， LI P，ZHANG Z H. Iterative soft compensation for OFDM systems with clipping and superposition coded modulation[J]. IEEE Transactions on Communications， 2010（10）： 2861-2870.

[6]WANG C L， WANG S S，CHANG H L. IEEE Wireless Communications and Networking Conference （WCNC）：A Low-complexity SLM Based PAPR Reduction Scheme for SFBC MIMO-OFDM Systems，March 28-31，2011[C].Mexico：IEEE， 2011.

[7]YADAV S S， PRADHAN P K， PARRA S K. Computer， Communication， Control and Information Technology （C3IT）：Computational Complexity Analysis of PTS Technique Under Graphics Processing Unit，February 25-26，2015[C]. Hooghly：IEEE，2015.

（编辑 王永超编辑）

Improved partial transmission sequence algorithm based on Hadamard matrix

Guo  Wei¹， Liu  Hao^2*

（1.Rizhao Radio Monitoring Station， Rizhao 276800， China; 2.Rizhao Jiaoneng Electric Power Engineering

Co.， Ltd.， Rizhao 276800， China）

Abstract：  PTS （Partial Transmission Sequence） is a commonly used method to reduce the PAPR（Peak-to-Average Power Ratio）of OFDM（Orthogonal Frequency Division Multiplexing）system， which ensures not to cause signal distortion for the system. The traversal characteristics of PTS algorithm result in a significant increase in computational complexity. The improved PTS algorithm based Hadamard matrix proposed in this paper greatly ensures the signal PAPR performance while significantly reduces the complexity of the calculation process.

Key words： orthogonal frequency division multiplexing; peak to average power ratio; partial transmission sequence