计数原理单元测试卷（B卷）

张旭要

一、单选题（本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。）

1.将4个6和2个8随机排成一行，则2个8不相邻的情况有（ ）。

A.480种 B.240种

C.15种 D.10种

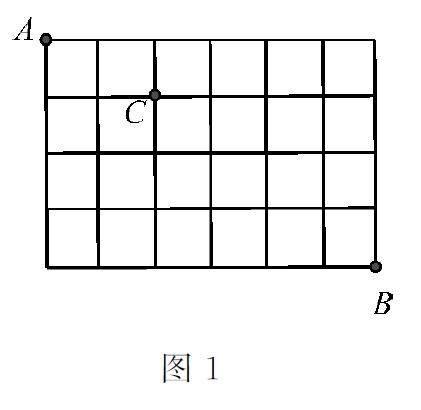
2.在某城市中，A，B两地有如图1 所示的方格形道路网，甲随机沿道路网选择一条最短路径，从A 地出发去往B 地，途经C 地，则不同的路线有（ ）。

A.90 种 B.105 种

C.260种 D.315 种

3.甲、乙、丙、丁4个学校将分别组织部分学生开展研学活动，现有A，B，C，D ，E 这5个研学基地供选择，每个学校只选择一个基地，则4个学校中至少有3个学校所选研学基地不相同的选择种数为（ ）。

A.420 B.460 C.480 D.520

4.甲、乙、丙、丁、戊、己6人站成一排拍合照，要求甲必须站在中间两个位置之一，且乙、丙2人相邻，则不同的排队方法共有（ ）。

A.24种 B.48种

C.72种 D.96种

5.某学校为增进学生体质，拟举办长跑比赛，该学校高一年级共有20个班级，现将22个参赛名额分配给这20个班级，每班至少1 个参赛名额，则不同的分配方法有（ ）。

A.210种 B.200种

C.150种 D.100种

6.将甲、乙等5位同学分别保送到北京大学、上海交通大学、浙江大学3 所大学就读，则每所大学至少保送1人的不同保送方案有（ ）。

A.240种 B.180种

C.150种 D.540种

7.（3x-2）（x-1）6 的展开式中x3 的系数为（ ）。

A.85 B.5 C.-5 D.-85

8.某学校准备开设4门劳动课程：“蔬菜种植”“绿植修剪”“糕点制作”“电动自行车修理”。开课之前，要安排4男2女共6名教师参加这4门劳动课程的技术培训，要求每一项培训都要有教师参加，每位教师只能参加其中一门培训，其中“蔬菜种植”必须安排2位教师，“电动自行车修理”不安排女教师，“糕点制作”不安排男教师，则不同的安排方法有（ ）。

A.132种 B.112种

C.96种 D.84种

二、多选题（本题共4小题，每小题5分，共20分。在每小题给出的选项中，有多项符合题目要求。全部选对的得5分，部分选对的得2分，有选错的得0分。）

9.2023年国外某智库发布尖端技术研究国家竞争力排名，在极超音速和水下无人机等23个领域中，有19个领域中国处于领先地位。某科技博主从这19个领域中选取了A，B，C，D，E，F 这6个领域，准备在2024年10月1—6日对公众进行介绍，每天随机介绍其中一个领域，且每个领域只在其中一天介绍，则（ ）

A.A，B 在后3 天介绍的方法种数为144

B.C，D 相隔一天介绍的方法种数为96

C.E 不在第一天，F 不在最后一天介绍的方法种数为504

D.A 在B，C 之前介绍的概率为1／3

10.若（1+x）+（1+x）2+…+（1+x）n=a0+a1x+a2x2 +…+anxn ，且a0 +a1 +a2+…+an-1+an =126，则下列结论正确的是（ ）。

A.n=6

B.a1+a2+a3+…+an-1=119

C.（1+2x）n 的展开式中二项式系数的和为729

D.a1+2a2+3a3+…+nan =321

11.关于（x2+1／x2-2）3的展开式，下列结论正确的是（ ）。

A.所有项的二项式系数之和为32

B.所有项的系数之和为0

C.常数项为-20

D.系数最大的项为第3项

12.若一个三位数中十位上的数字比百位上的数字和个位上的数字都大，则称这个数为“凸数”。如231、354等都是“凸数”。若用1，2，3，4，5这5个数字组成无重复数字的三位数，则（ ）。

A.组成的三位数的个数为30

B.在组成的三位数中，奇数的个数为36

C.在组成的三位数中，“凸数”的个数为24

D.在组成的三位数中，“凸数”的个数为20

三、填空题（本大题共4 小题，每小题5分，共20分。）

13.现有5名同学从北京、上海、深圳三个路线中选择一个路线进行研学活动，每个路线至少1人，至多2人，其中甲同学不选深圳路线，则不同的路线选择方法共有种。（用数字作答）

14.组合数C0 34+C2 34+C4 34+…+C34 34 被9除的余数是_____。

15.某校高二（1）班要举办一场晚会，有2个歌唱、2个舞蹈、1个小品、1个相声共6个节目，要求2个歌唱不相邻演出，且2个舞蹈不相邻演出，则这6个节目共有_____种不同的演出顺序。

16.（x2+y+3）6 中x4y 的系数为_____。（用数字作答）

四、解答题（本大题共6小题，共70分，解答时应写出文字说明、证明过程或演算步骤。）

17.（本小题10 分）（1）已知Cm5=C25m-1（m >1），求Cm6+Cm+1 6 +Cm+2 7 +Cm+3 8 的值。（用数字作答）

（2）解不等式3A3x+1≤2A2x+2+6A2x+1。

18.（本小题12分）已知f（x）=（3根号下x2 +3x2）n 的展开式中各项的系数和比各项的二项式系数和大992。

（1）求展开式中二项式系数最大的项;

（2）求展开式中系数最大的项。

19.（本小题12 分）为弘扬我国古代的“六艺”文化，某夏令营主办单位计划利用暑期开设“礼”“乐”“射”“御”“书”“数”六门体验课程。

（1）若体验课连续开设六周，每周一门，求其中“射”不排在第一周，“数”不排在最后一周，求所有可能的排法种数;

（2）甲、乙、丙、丁、戊五名教师在教这六门课程，每名教师至少任教一门课程，求其中甲不任教“数”的课程安排方案种数。

20.（本小题12分）按下列要求分配6本不同的书，求各有多少种不同的分配方法。

（1）分成三份，1份1本，1份2本，1份3本;

（2）甲、乙、丙三人中，一人得1本，一人得2本，一人得3本;

（3）平均分成三份，每份2本;

（4）平均分配给甲、乙、丙三人，每人2本;

（5）分成三份，1份4本，另外两份每份1本;

（6）甲、乙、丙三人中，一人得4本，另外两人每人得一本。

21.（本小题12 分）设（1+x）n =a0 +a1x+a2x2+…+anxn ，n≥4，n∈N* 。已知a23=2a2a4。

（1）求n 的值;

（2）若（1+根号下3）n =a+b根号下3，其中a，b∈N* ，求a2-3b2 的值。

22.（本小题12分）现有0，1，2，3，4，5这6个数字。

（1）可组成多少个没有重复数字的偶数？

（2）在组成没有重复数字的五位数中，按从小到大排21 350是第几个数字？

（责任编辑 徐利杰）