计数原理单元测试卷(A卷)

曲海胜

一、单选题（本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。）

1.从4名男生与3名女生中选2人去参加一场数学竞赛，则男女生各1人的不同的选派方法数为（ ）。

A.7 B.12 C.18 D.24

2.2023年夏天贵州榕江的村超联赛火爆全国，吸引了国内众多业余球队参赛。现有6个参赛队伍代表站成一排照相，其中贵阳折耳根队与柳州螺蛳粉队必须相邻，同时南昌拌粉队与温江烤肉队不能相邻，那么不同的站法共有（ ）种。

A.144 B.72 C.36 D.24

3.已知C7n+1=C7n+C8n（n∈N* ），则n=（ ）。

A.14 B.15 C.13 D.12

4.北斗七星是夜空中的七颗亮星，我国汉代纬书《春秋运斗枢》就有记载，它们组成的图形像我国古代舀酒的斗，故命名北斗七星。北斗七星不仅是天上的星象，也是古人藉以判断季节的依据之一。如图1所示，用点A，B，C，D ，E，F，G 表示某一时期的北斗七星，其中B，D ，E，F 看作共线，其他任何3个点均不共线，过这7个点中任意2个点作直线，所得直线的条数为（ ）。

A.4 B.13 C.15 D.16

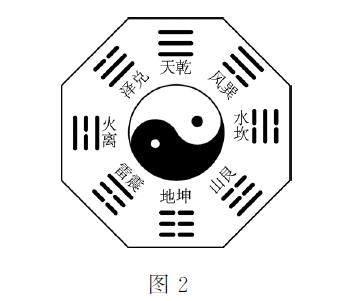
5.如图2所示，古代中国的太极八卦图是以同圆内的圆心为界，画出形状相同的两个阴阳鱼，阳鱼的头部有个阴眼，阴鱼的头部有个阳眼，表示万物都在相互转化，互相渗透，阴中有阳，阳中有阴，阴阳相合，相生相克，蕴含现代哲学中的矛盾对立统一规律。由八卦模型图可抽象得到正八边形，从该正八边形的8个顶点中任意取出4个构成四边形，其中梯形的个数为（ ）。

A.16 B.20 C.24 D.28

6.在（1-x2）（x-1／x）6的展开式中，含x2 项的系数是（ ）。

A.-20 B.5 C.15 D.35

7.某学校派出5名教师去3所乡村学校支教，其中有一对教师夫妇参与支教活动。根据相关要求，每位教师只能去1所学校参与支教，并且每所学校至少有1名教师参与支教，同时要求这对教师夫妇必须去同所学校支教，则不同的安排方案有（ ）。

A.18种 B.24种

C.36种 D.48种

8.中国南北朝时期的著作《孙子算经》中，对同余除法有较深的研究，设a，b，m（m >0）均为整数，若a 和b 被m 除得的余数相同，则称a 和b 对模m 同余，记为a≡b（modm）。如9 和21 被6 除得的余数都是3，则记9≡21（mod6）。若a≡b（mod10），且a=C0 20+C1 20·2+C2 20·22+…+C2200·220，则b 的值可以是（ ）。

A.2 019 B.2 020

C.2 021 D.2 022

二、多选题（本题共4小题，每小题5分，共20分。在每小题给出的选项中，有多项符合题目要求。全部选对的得5分，部分选对的得2分，有选错的得0分。）

9.下列结论正确的是（ ）

（2）女生互不相邻的坐法有多少种？

（3）甲、乙两位同学相邻且都不与丙同学相邻的坐法有多少种？ （列出算式，并计算出结果）

18.（本小题12分）（1）解关于x 的不等式Ax8<6Ax8-2。

（2）求等式C5n-1+C3n-3／C3n-3 =195中n 的值。

19.（本小题12分）已知集合A={x|1

（1）从A∪B 中取出3个不同的元素组成三位数，则可以组成多少个？

（2）从集合A 中取出1个元素，从集合B 中取出3个元素，可以组成多少个无重复数字且比4 000大的正整数？

20.（本小题12分）已知（ax- 1／根号下x）n（a∈R，n∈N* ）的展开式的前三项的二项式系数之和为22，所有项的系数之和为1。

21.（本小题12分）用1，2，3，4，5，6这6个数字，可以组成多少个无重复数字的：

（1）四位偶数？

（2）数字1、3、5互不相邻的六位数？

（3）六位数？ 其中数字6、4、1按自左至右的顺序保持不变（如634 512，562 431）。

注：所有结果均用数值表示。

22.（本小题12分）已知（a-2x）8=a0+a1（x-1）+a2（x-1）2+…+a8（x-1）8，其中实数a>0，且x2 的系数为81 648。

（1）求实数a 的值。

（2）计算：（ⅰ）（a0+a2+a4+a6+a8）·（a1+a3+a5+a7）;

（ⅱ）|a0|+|a1|+|a2|+ … +|a8|。（结果用幂的形式表示）

（责任编辑 徐利杰）