一种基于金融时间序列数据的深度学习风险预测方法
朱林
摘要:金融时间序列数据的指标按照不同的会计准则会得到不同的数值,如何取舍会受到人为因素的干预。针对金融时序数据的领域泛化专门提出一种异常检测方法,解决特征分布的多样性和复杂性,捕捉金融序列数据的特有表征模式。将循环神经网络之后获得的结果仅作为学习到的知识,通过标准分类器在特征空间对其边缘分布进行适配,然后再通过隐变量自回归模型进一步进行预测,以此来提高预测的精度。然后,构建一个隐变量自回归模型来进行风险预测,通过捕捉金融时间序列数据之间的特征分布来识别其中的金融风险,实验结果表明,模型具有一定的可行性。
关键词:深度学习;金融时间序列数据;特征分布;金融风险;异常检测
一、前言
深度学习已经被广泛应用于计算机视觉和自然语言处理领域。但是与图像领域和自然语言处理领域有较多的经典网络结构可选择不同,金融时间序列数据处理吸引了大批研究者探索其未来研究的方向。尝试使用深度学习技术增强金融风险防范措施,无论在基础理论研究上还是对于国民经济和社会发展中的金融风险防范工作,都具有很高的研究和应用价值。
二、深度学习技术在金融风险预测领域的作用
异常检测是一门由来已久的技术,已经广泛应用于各个领域。随着近些年深度学习技术的突飞猛进,两项技术的集合受到了诸多研究者的关注,并且也在一些领域展开了应用,网络入侵检测[1]、智慧医疗[2]、传感器网络[3],以及视频异常检测[4]等。一个金融时间序列数据的指标按照不同的会计准则会得到不同的数值,如何取舍会受到人为因素的干预。当前被判定合规的数据标签,在金融风险真实发生后再回溯人工智能的学习过程,相当于非主观有意地对模型数据进行“投毒”。有研究者注意到,深度学习模型,无论卷积神经网络还是循环神经网络提取到的特征都具有相似性和继承性[5],尝试将其应用在其他具备一定特征的金融时序数据集上进行泛化研究,对于探索深度学习在金融风险预测工作上的有效性具有应用意义。与其他很多异常检测场景不同,在实务中,金融风险不一定意味着损失,也可能是套利的机会。在金融时间序列数据场景下获得准确的标签的代价是十分昂贵的,尤其是异常数据在一开始往往会标记成正常数据,因为事件之初,总有各种各样的解释背书该操作的合理合规性。如何通过多源时序数据的时空关联性来发现通用表征模式,不同的是这里误导模型的将不再有噪声数据,而是并不太准确,事后往往被发现错误标注的标签数据。这是金融时序数据场景下异常检测面临的另一个关键挑战。
本文提出一种针对金融时序数据的领域泛化异常检测方法,解决特征分布的多样性和复杂性,捕捉金融序列数据的特有表征模式。该方法基于循环神经网络,但在架构上分为两个学习模块。在两个学习模块之间具有学习到的特征知识的传递,先在一个源领域上进行pre-train,使用循环神经网络作特征提取模块,然后在目标领域上进行隐变量的自回归分析(latent autoregressive models)。
三、研究方案
(一)将数据的学习和使用分为两个部分
在该模型中,金融时间序列数据领域所有的标签被认为都只有在事后才能明确其准确性。那么,该模型的设计方案中在循环神经网络之后获得的结果仅把它当做学习到的知识,通过标准分类器在特征空间对其边缘分布进行适配,然后再通过隐变量自回归模型进一步进行预测,通过这样的方法来提高预测的精度。
(二)使用隐变量自回归模型寻找金融风险的分布特征
该研究使用隐变量自回归模型计算预测值与标签之间的分布距离,对于特征空间进行分布适配。虽然大多数深度研究的前提都是满足独立同分布这一要求,金融时间序列数据相较于其他数据集在这一点上矛盾并不突出,但也不能认为在严格意义上完全符合。假设在其他时间序列中的噪音,在该领域指不由各种机构有意操控的数据分布下的金融时间序列数据。在更多考虑金融时间序列数据的时间依赖性、空间依赖性,以及金融“噪音”数据分布的各种影响后,通过当前的方案使得正常数据在隐变量特征空间具有独立同分布这一特性,在没有添加生成数据的同时可以提高研究模型的鲁棒性。
四、方案设计
(一)复合深度学习框架
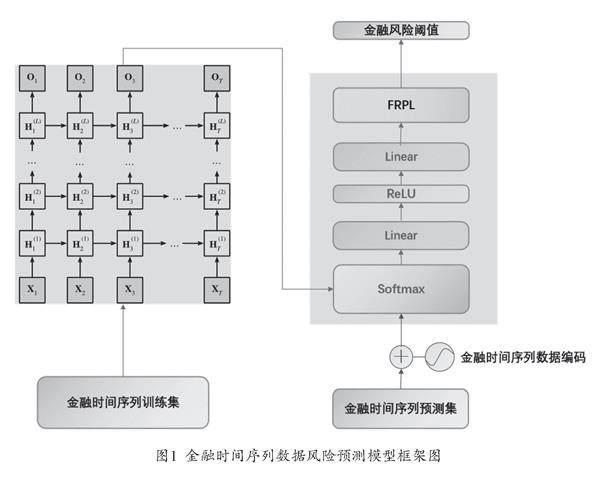
本研究中对深度学习各种模型的层次架构进行操作,建立一个可以互相衔接使用的数据处理学习机制架构。构建由循环神经网络与隐变量自回归模型组合的复合架构如图1所示,旨在通过隐变量的特征学习,将过去时间金融数据以及其在隐变量自回归模型中预测产生的误差,再进行统一的学习。
在金融时间序列数据中,每个金融机构包含m个指标、n个(n>1)金融机构的数据集,定义S表示指标集合,模型所获得的金融时间序列数据总体有N=|S|=mn个指标,每一个指标为xi∈S,xi∈Rti×1。其中,ti表示指标xi的长度。目标限定在金融时间序列数据这一种时间序列上,完成对于金融风险的预测这一学习任务。利用相似性度量在大量金融数据集进行学习,通过学习找出金融数据时间序列计算风险阈值的较优方法。
假设当前某一机构的时间序列数据为Xi,那么向下一个隐变量自回归模型传递的特征知识由循环神经网络进行计算,如公式(1)。
(1)
其中,Ht-1是上一个时间点的该机构金融时间序列数据计算获得的特征知识,即X=(x1…,xN)T∈RN×T表示包含所有数据源的输入样本。
通过本研究的方式,寻找相邻时间隐变量Ht和Ht-1之间的关系,并将学习到的信息保留在当前时间的隐变量之中。这些隐变量在模型的下一个计算层,将被送入带有激活函数的全连接层。随后使用隐变量自回归算法来做金融时间序列数据集异常特征的线性预测,将不同机构的特征带入当前学习的特征中去进行隐变量自回归分析。利用特征空间中的数据分布信息来探测当前数据源的特征是否异常。按照既定的研究目标将循环神经网络在指定金融时间序列数据集内学习到的特征知识表示作为隐变量自回归模型的输入。
对于金融时间序列数据集中的标签与模型预测值之间的距离,当前研究使用交叉熵来进行计算。为了考虑一个机构的金融时间序列数据集在前后时间线上的预测差距规模,使用时间累积影响度这个值来衡量整个序列中所有时间预测值之间的交叉熵损失,如公式(2)。
(2)
前置循环神经网络计算金融时间序列数据的训练数据,学习获得符合独立同分布要求的隐变量知识,再通过隐变量自回归模型学习获得金融时间序列数据集在相关机构、相关时间上的预测差距规模,如公式(3)。
(3)
λ为模型目标函数的超参数,用于调整误差之间的权重大小。LCEL 为前置循环神经网络的训练误差,该值指示了学习到的隐变量知识是否能够很好地保留输入样本的特征分布,这里误差计算使用交叉熵。LMSE表示隐变量自回归模型的训练误差,通过这个值考查正常情况与异常情况之间的距离,以探测金融风险。
最终通过深度学习获得的是一个风险阈值,它在不同金融场景下意义可能不同。对于金融机构,它可以是止盈止损阈值。对于监管机构,它可以是管控红线。这里的训练集X={x1,x2,…,xD},xi∈RN×T是包含风险存在的、真实的一个时间段内的特征集合。FRPL(xi)是对应样本标签xi在循环神经网络结合隐变量自回归模型训练之后得到的距离总和,u是其均值。η是超参数,通过这种模型的不断应用形成这个超参数的特征标签库之后,η也可以通过深度模型学习获得,如公式(4)。
(4)
在预测阶段,通过判断是否预测样本特征xi的距离FRPL(xi)>FRthreshold,如果大于,则该样本xi被标定为金融风险,反之为正常。
五、实验结果分析
(一)该模型与仅使用循环神经网络之间的比较
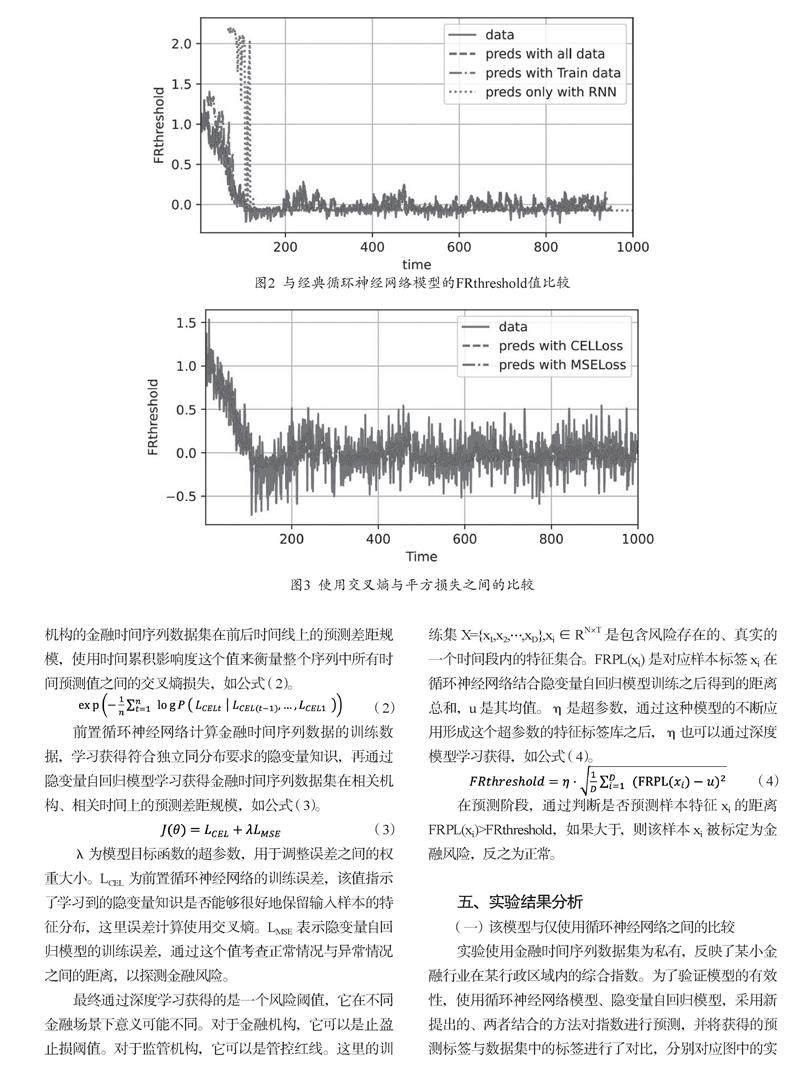
实验使用金融时间序列数据集为私有,反映了某小金融行业在某行政区域内的综合指数。为了验证模型的有效性,使用循环神经网络模型、隐变量自回归模型,采用新提出的、两者结合的方法对指数进行预测,并将获得的预测标签与数据集中的标签进行了对比,分别对应图中的实线段和点化线线段,如图2所示。可以看出在短期内该模型有预测能力,长期预测情况下,能力会被不断削弱,但也要强于全点线所对应的循环神经网络。
如果将预测测试集的数据也投入训练,可以得到图2中的虚线线段曲线,对于监管场景下的应用具有实践价值。
(二)该模型使用交叉熵与平方损失之间的比较
协变量漂移将会导致误差的积累,在数据脱离金融规律的循环之后,预测将不再准确,甚至会因为在模型内部达到某个奇点而造成自动梯度下降的算法失灵。即使来自于同一个行业,由于协方差漂移问题的存在,在源域特征分布与目标域特征分布之间也存在差异。该研究相较于异常检测中常规使用的LMSE,来度量这两个分布之间的差距,使用了交叉熵来处理这种距离损失。通过实验结果数据可以看出该模型取得了一个更好的效果,如图3所示。
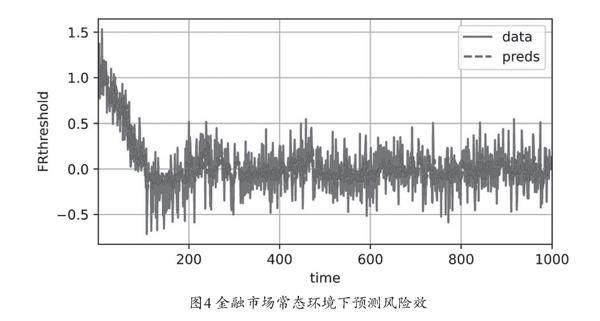
(三)金融市场常态环境下预测风险效果
如果给定的金融时间序列数据完全剔除金融市场中的黑天鹅事件、灰犀牛事件,该模型可以获得比较满意的结果,如图4所示。在应用于金融时间序列数据的特征分布比较稳定的情景下,该模型可以预测出该市场金融风险阈值的发展趋势。由于在金融时间序列中,正常和异常数据往往具有同一个类别的标签,考虑到其数据分布的差异性,实际上在不同阶段可以给这些数据集赋予新的伪标签。
六、结语
本研究具体方法是首先构建循环神经网络新的隐知识学习体系,然后,构建一个隐变量自回归模型来进行风险预测。通过捕捉金融时间序列数据之间的特征分布特征来识别其中的金融风险,实验结果表明,模型具有一定的可行性。
参考文献
[1] Chalapathy R, Chawla S. Deep learning for anomaly detection: A survey [J]. arXiv preprint arXiv:1901.03407, 2019.
[2] Litjens G, Kooi T, Bejnordi B E, et al. A survey on deep learning in medical image analysis [J]. Medical image analysis, 2017, 42: 60-88.
[3]Ball J E, Anderson D T, Chan C S. Comprehensive survey of deep learning in remote sensing: theories, tools, and challenges for the community [J]. Journal of Applied Remote Sensing, 2017, 11(04): 042609.
[4]Kiran B, Thomas D, Parakkal R. An overview of deep learning based methods for unsupervised and semi-supervised anomaly detection in videos [J]. Journal of Imaging, 2018, 4(02): 36.
[5]Zhang Y, Chen Y, Wang J, et al. Unsupervised deep anomaly detection for multi-sensor time-series signals[J]. IEEE Transactions on Knowledge and Data Engineering, 2021, 35(02): 2118-2132.
基金项目:1.贵州省第六批千层次人才项目(项目编号:筑科合同-GCC[2022]011);2.2024年度贵州省基础研究计划(自然科学类)项目“基于金融数据的时间序列在线深度迁移学习研究”(项目编号:黔科合基础-ZK[2024]一般520)
作者单位:贵阳学院电子信息工程学院
■ 责任编辑:王颖振、郑凯津

