纤维缠绕管的挂钉工艺参数研究

陈东方，崔启玉，张恒，任俊伟

摘要小缠绕角度的纤维缠绕圆管，因缠绕转向区长度过长而常采用挂钉缠绕工艺。转向区长度是挂钉缠绕工艺的关键技术参数，其由圆管直径、缠绕角、摩擦系数决定。除此之外，纤维缠绕挂钉工艺参数还包括转向区（挂钉区）的挂钉轴向排数、挂钉轴向位置、挂钉环向钉距（或钉数）、挂钉的钉高钉径等工艺参数。本文通过纤维缠绕基础理论公式和数值模拟仿真方法，研究缠绕角度、摩擦系数对于缠绕转向区转长直径比的影响变化规律，使得工程师可以快速根据缠绕角和摩擦系数计算出转长直径比，进而结合圆管直径评估出转向区长度。通过公式计算和软件模拟验证，54.7°缠绕角且0.12摩擦系数时，转长直径比为0.94；45°缠绕角且0.12摩擦系数时，转长直径比为1.73。最后基于临界转长直径比（kL=1），给出圆管类纤维缠绕工艺的三种技术路线，即传统圆管缠绕工艺、柱面转向挂钉工艺、端面转向挂钉工艺。

关键词纤维缠绕；工艺仿真；转长直径比；挂钉缠绕工艺

Pins Winding Parameters for Fiber Winding Circular Tube

CHEN Dongfang1， CUI Qiyu2 ， ZHANG Heng1， REN Junwei1

（1.CRRC QINGDAO SIFANG CO.，Ltd.， Qingdao  266111；2.Beijing Intelligent United Innovation Technology Co.，Ltd.， Beijing 100027）

ABSTRACTThe fiber winding circular-tube with small winding angle be used pins winding process because the winding turning length is too long.The winding turning length is a key technical parameter of the pins winding process， which is determined by the diameter ， winding angle， and friction coefficient. In addition， the pins winding process parameters also include the number of axial pin rows of in the winding turning area （the pins winding area）， the axial position and axial distance of pin rows， the pins distance （the pins number） in the circumferential direction，the pins height and the pins diameters. In this paper， the influence of winding angle and friction coefficient on the turning length-diameter ratio of the winding turning area is studied by using the basic theoretical formula of filament winding and the method of numerical simulation.Through formula calculation and software simulation verification， when the winding angle is 54.7°and the friction coefficient is 0.12， the turning length-diameter ratio is 0.94; when the winding angle is 45°and the friction coefficient is 0.12， the turning length-diameter ratio is 1.73.Finally， based on the critical turning length-diameter ratio is 1， three technical roadmap of filament winding process for circular-tube winding is traditional circular-tube winding process， cylindrical-face turning pins process and end-face turning pins process.

KEYWORDSfilament winding；process simulation；turning length-diameter ratio；pins winding process

1引言

复合材料纤维缠绕圆管是较为典型复合材料应用产品，由于具有比强度高、比模量高、线膨胀系数小、抗疲劳、阻尼性能好等优点［1］，广泛应用于轻量化高性能的结构件，例如移动式桥梁构件、抗扭传动轴、抗弯机辊、地铁构架横梁、高速列车吸能管、地铁抗侧滚扭杆、无人机支撑构件、卫星的天线支架、太阳能电池帆板支架、鱼竿、登山杖和高尔夫杆等。随着圆管类纤维缠绕制品应用领域的拓展，对纤维树脂材料、缠绕设备、缠绕工艺设计、长度利用率提出了更高技术要求，需要不断进行技术创新和改进。

然而，圆管类纤维缠绕工艺技术在实际应用中仍面临一些技术挑战和问题。例如，塑料薄膜生产设备用的塑料薄膜机辊要求具有较高的抗弯性能，近零度缠绕角度纵向螺旋缠绕层可以提供这样的抗弯能力，此类纤维缠绕机辊的突出工艺问题是筒件有效缠绕长度之外的转向区长度过长。如何根据定长缠绕工艺要求［2］，避免在管道端部出现滑纱、加减速段过长［3］（转向区长度过长），应用挂钉缠绕工艺控制转向区长度，提高此类圆管类缠绕制品的长度利用率是缠绕工艺设计时需要考虑的重要问题。

自1980年以来，经过科研工作者研究探索和工程实践，完善了纤维缠绕基础理论，开发出纤维缠绕工艺设计数值模拟仿真软件。本文基于圆柱体变角度非测地线缠绕公式［3］和纤维缠绕工艺设计数值模拟仿真软件，旨在对圆管类纤维缠绕的转向区长度计算进行系统的研究分析，通过电子表格和曲线图方式，重点探讨缠绕角度α和摩擦系数f对缠绕转向区转长直径比kL的影响及其变化规律。

基于转向区长度计算公式，提出转长直径比kL和临界转长直径比（kL1）两个技术参数，使得工程师可以直接根据缠绕角和摩擦系数快速地计算出转长直径比kL，并根据规定临界转长直径比（kL=1）快速地规划出圆管类纤维缠绕工艺的技术路线（传统圆管缠绕工艺、柱面转向挂钉工艺、端面转向挂钉工艺）。随后，给出挂钉缠绕工艺涉及的技术参数的确定原则和和计算方法。技术参数包括钉排轴向排数、钉排轴向位置、挂钉环向间距、挂钉环向钉数、钉排环错间距、挂钉高度、挂钉直径等。

2研究内容

2.1转向长度计算

1990年冷兴武著的《纤维缠绕原理》［4］书中论述的圆柱体非测地线稳定公式：

L=±kRf（1/sinα1-1/sinα2）=L=±Rf/k（1/sinα1-1/sinα2）（1）

公式（1）为圆柱体非测地线稳定公式，式中L为圆柱体计算段长度、k为滑线安全系数（书中提及数控缠绕机传动稳定且张力控制好，k取值小些；而对于机械式缠绕机因传动不稳且张力控制不好，k取值为2）、R为圆柱体半径、f为纤维层间静摩擦系数（书中提及对于玻璃纤维摩擦系数取值范围为0.10-0.13）、α1和α2为圆柱体计算段的起点缠绕角和终点缠绕角。

基于上述公式，如果将书中提及的摩擦系数f与滑线安全系数的综合作用称为缠绕滑线系数λ=f/k。由于滑线安全系数取值范围1-2，故此缠绕滑线系数λ≤f，设置滑线安全系数k=1为理想值，而非理想值情况下，将造成缠绕滑线系数λ小于实际摩擦系数f，更容易出现滑纱工艺问题。

2016年赫晓东等著的《先进复合材料压力容器》［5］书中论述了纤维缠绕稳定不滑纱条件：

|Fs|=|Fn|·|kn|，λ|kg|/|kn|=kf（2）

公式（2）为缠绕滑线系数公式，式中Fs缠绕纤维在切平面上的分量侧滑力，Fn缠绕纤维在法上的分量正压力，kg为曲面测地曲率，kn为曲面法曲率，λ为缠绕滑线系数，k为滑线安全系数，f为摩擦系数。

此书中提及摩擦系数f小于1，最大缠绕滑线系数λmax小于1，取值范围在0-1之间；故此缠绕滑线系数λ≤f，由此可知滑线安全系数取值范围为0-1。

根据两本书中提到的缠绕滑线系数λ、摩擦系数f、及滑线安全系数的关系式，殊途同归只是论述出发点不同，造成滑线安全系数的取值范围不同。本文采用公式2中的滑线安全系数的取值范围0-1，并设定k=1为其理想值；在摩擦系数不变情况下，滑线安全系数减小带来缠绕滑线系数减小，导致圆柱体计算段长度增大。故此，圆柱体非测地线稳定公式改写为：

L=±Rkf（1/sinα1-1/sinα2）L=D2kf

|1/sinα1-1/sinα2|（3）

公式（3）圆柱体非测地线稳定的改写公式，式中L为圆柱体计算段长度，R为圆柱体半径（D为圆柱体直径），k为滑线安全系数（取值范围0-1），f为摩擦系数，α1和α2为圆柱体计算段的起点缠绕角和终点缠绕角。

本文根据公式（3）提出转长直径比概念，在滑移安全系数为理想值时，且圆筒两端回程的缠绕角为90°情况下，将转长直径比转换为只与筒身缠绕角α2和摩擦系数f相关的转长直径比公式。随后，通过仿真软件验证并确定。

L=D2kf|1sinα1-1sinα2|

kL=LD，α2=90kL=12kf|1sinα1-1|k=1，kL=12f|cscα2-1|（4）

L=D2kf|1sinα1-1sinα2|，U=L+bp2

kL=L+bp2D，α2=90kL=12kf|cscα2-1|+bp2D（5）

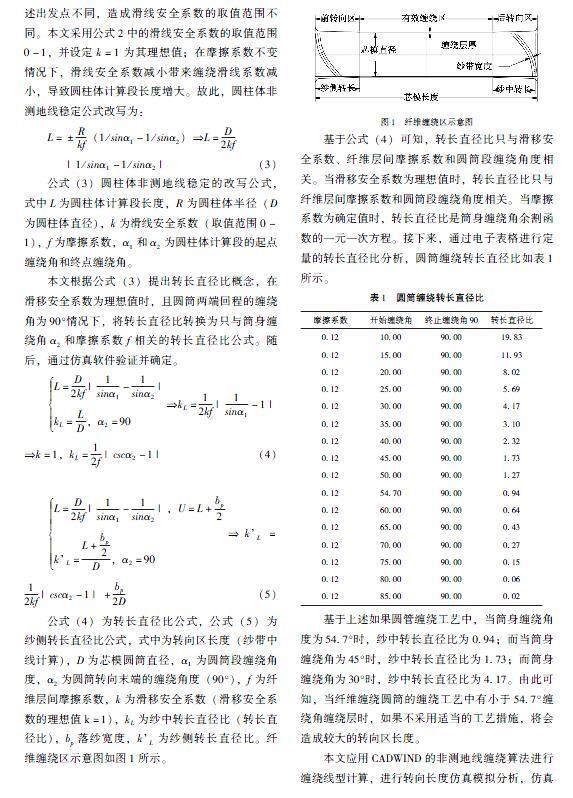
公式（4）为转长直径比公式，公式（5）为纱侧转长直径比公式，式中为转向区长度（纱带中线计算），D为芯模圆筒直径，α1为圆筒段缠绕角度，α2为圆筒转向末端的缠绕角度（90°），f为纤维层间摩擦系数，k为滑移安全系数（滑移安全系数的理想值k=1），kL为纱中转长直径比（转长直径比），bp落纱宽度，kL为纱侧转长直径比。纤维缠绕区示意图如图1所示。

基于公式（4）可知，转长直径比只与滑移安全系数、纤维层间摩擦系数和圆筒段缠绕角度相关。当滑移安全系数为理想值时，转长直径比只与纤维层间摩擦系数和圆筒段缠绕角度相关。当摩擦系数为确定值时，转长直径比是筒身缠绕角余割函数的一元一次方程。接下来，通过电子表格进行定量的转长直径比分析，圆筒缠绕转长直径比如表1所示。

基于上述如果圆管缠绕工艺中，当筒身缠绕角度为54.7°时，纱中转长直径比为0.94；而当筒身缠绕角为45°时，纱中转长直径比为1.73；而筒身缠绕角为30°时，纱中转长直径比为4.17。由此可知，当纤维缠绕圆筒的缠绕工艺中有小于54.7°缠绕角缠绕层时，如果不采用适当的工艺措施，将会造成较大的转向区长度。

本文应用CADWIND的非测地线缠绕算法进行缠绕线型计算，进行转向长度仿真模拟分析，仿真计算45°和54.7°两个缠绕角度的转向区长度，验证本文推导的转向长度的公式计算结果。为了减少线型闭合计算带来的计算结果偏差，尽可能使用较小的工艺纱宽（本案例工艺纱宽bp=2）。仿真软件计算结果如表2所示。

缠绕工艺参数：为了方便进行结果分析，本文使用芯模直径100 mm、筒身长度500 mm，两端转向区长度200 mm。

（1）45°缠绕角的工艺参数及仿真计算结果：

非测地线转入参数：缠绕角度：45°，摩擦系数：0.12，切点数：10/9，覆盖度：100 %。

非测地线型计算结果：缠绕角度：44.754° -45.003°，覆盖度：99.612 %-100.04 %，缠绕圈数：111，切点数：10/9，前转向区缠绕长度：172.2 mm，后转向区缠绕长度：174.57 mm。

（2） 54.7缠绕角的工艺参数及仿真计算结果：

非测地线转入参数：缠绕角度：54.7°，摩擦系数：0.12，切点数：-1/1，覆盖度：100 %。

非测地线型计算结果为缠绕角：54.696°-54.701°，覆盖度：100.35 %-100.36 %，缠绕圈数：91，切点数：-1/1，前转向区缠绕长度：93.493 mm，后转向区缠绕长度：93.745 mm。

（3）缠绕工艺软件CADWIND的仿真模拟结果如表2所示。

（4）CADWIND软件中给出的摩擦系数参考值列表，用于指导工程实践中的摩擦系数设置。实际工程应用中，由于树脂应用类型、缠绕时的环境温度和树脂粘度不同，用户需要实际测量使用。

从软件仿真计算结果分析可知，理想情况下转向长度公式的计算结果与软件仿真的模拟结果相当，即转长直径比kL只与纤维层间摩擦系数f和圆筒段缠绕角度α1相关。应用转向长度公式的计算结果与软件仿真的模拟结果之间存在少许的偏差。偏差产生原因在于应用CADWIND非测地线进行缠绕线型计算时，不仅需要计算转向长度，还要兼顾缠绕线型闭合计算。

2.2挂钉缠绕工艺

2.2.1缠绕路线的选择

本文以转长直径比为目标参数进行转向区长度控制，将临界转长直径比设置为1，可推导出临界转长直径比对应缠绕角近似为54.7°。随后，根据圆管缠绕的最小工艺缠绕角和芯模转向区长度设计要求，将纤维缠绕圆管工艺路线选择分为传统圆管缠绕工艺、柱面转向挂钉工艺、端面转向挂钉工艺三种。如果实际工程中芯模长径比较小，为了控制合理长度利用率，可以采用多件同时缠绕随后切割方案。

（1）工艺路线1

传统圆筒缠绕工艺，适用于缠绕角大于54.7°缠绕工艺，其转长直径比小于临界转长直径比1，纤维轨迹在圆柱表面进行转向缠绕。实际缠绕过程中，摩擦系数设置值与实际相当，转向区不存在滑纱问题，适用于3轴数控缠绕机床。

非测地线输入参数：缠绕角：54.7°，摩擦系数：0.12，纱带总宽：6。

（2）工艺路线2

柱面转向挂钉工艺，适用于缠绕角小于54.7情况，且转长直径比设计为1，且不方便采用端面转向挂钉工艺时，可以采用柱面转向挂钉工艺。为了尽可能控制转向区滑纱因素造成的主缠绕区缠绕角变化，宜采用转向区开始阶段2排挂钉、转向区结束阶段1排挂钉的工装设计。实际缠绕过程中，摩擦系数设置值大于实际值，纤维轨迹进入转向区后有滑纱问题，挂钉近筒身区设置，适用于3轴数控缠绕机床。

非测地线输入参数：缠绕角：30°，摩擦系数：0.55，纱带总宽：6。

（3）工艺路线3

端面转向挂钉工艺，适用于缠绕角小于54.7情况，且转长直径比设计为1，可以在圆筒端面进行纤维轨迹转向。为了尽可能控制转向区滑纱因素造成的主缠绕区缠绕角变化，宜采用转向区结束阶段前1排挂钉的工装设计。实际缠绕过程中，摩擦系数设置值与实际相当，在端面棱角处有滑纱，挂钉近端面设置，适用于4轴数控缠绕机床。

非测地线输入参数：缠绕角：30°，摩擦系数：0.12，纱带总宽：6。

2.2.2挂钉工艺的参数

当圆筒缠绕工艺存在小缠绕角时，筒件有效缠绕长度之外的转向区长度过长，这时需要采用挂钉缠绕工艺进行缠绕生产。本文，将54.7°缠绕角设置为挂钉缠绕工艺与非挂钉缠绕工艺的临界缠绕角（或按实际情况考虑），挂钉工艺的挂钉布置参数见图8。当采用挂钉缠绕工艺时，我们需要考虑挂钉工艺参数包括：

（1）轴向布置参数：挂钉轴向排数、挂钉轴向位置；

（2）环向布置参数：挂钉环向距离（或环向钉数）、钉排环向错列角；

（3）挂钉钉高钉径：首钉排钉高，尾钉排钉高，挂钉钉径包括避免发生永久塑性变形的挂钉强度计算、及避免发生较大弹性变形的弯曲挠度控制。

2.2.3挂钉的排数位置

挂钉的排数设置，主要根据转向区的摩擦系数设置与实际摩擦系数的变化程度。为了控制缠绕区的缠绕角稳定性，我们需要缠绕角变化初始阶段进行两排挂钉控制，缠绕角变化结束阶段进行一排挂钉控制；如果转向区的摩擦系数设置与实际相当，可以采用一排挂钉控制。

挂钉工艺的钉排轴向布置参数：包括钉排轴向位置、钉排轴向数量和钉排轴向距离。钉排轴向位置分为位于转向区开始的首钉排、转向区结束的尾钉排和两排之间的中钉排；钉排轴向布置原则为“其安易持、未兆易谋”原则进行，即在超过实际摩擦系数设置区域之前设置钉排。三个钉排的排距包括首尾排距和首中排距。挂钉工艺的多组钉排布置参数：首钉排与中钉排的轴向距离和环向错列角度。

挂钉工艺的钉排环向布置参数：包括挂钉环向钉距（或环向钉数），各个挂排的挂钉高度（钉高）和挂钉直径（钉径）。

2.2.4挂钉的钉数间距

挂钉的数量和挂钉的环向距离，主要根据纱带宽度和缠绕圈数进行设置。挂钉的环向距离可以根据一个纱带宽度进行设置。

2.2.5挂钉的钉高设计

挂钉钉高：挂钉钉高根据缠绕层厚度确定，转向区的缠绕层厚度为变厚度，转向区开始段厚度与筒身缠绕层厚度相当，故此首钉排和中钉排的挂钉高度，可以采用2-3倍的筒身缠绕层厚度为参考；转向区结束段缠绕层厚度较厚，相对筒身缠绕层厚度通常有4倍以上，故此尾钉排的挂钉高度，可以采用5-6倍的筒身缠绕层厚度为参考；鉴于此圆筒末端有条件设置积纱槽。矩形截面或椭圆形截面等异性截面管件的挂钉高度应以异性截面的最大旋转直径为基准进行设计，异型截面的最大参考直径如图9所示；因为缠绕后处理程序通常参考异性截面的最大旋转直径进行安全距离设置。

2.2.6挂钉的钉径计算

当纤维通过钉端时，其受力近似悬臂梁受力结构，挂钉直径主要考虑纤维通过钉端时抗弯强度（塑性变形）和弯曲挠度（弹性变形）。如果挂钉直径过小，纤维经过钉端时发生弯曲塑性变形被拉弯，落纱点位置发生变动，将影响缠绕角准确性；如果挂钉不被拉弯，纤维经过钉端时存在较大挠度，落纱点位置也发生变动，将影响缠绕角准确性。故此挂钉直径计算，应先按抗弯强度计算，再进行挠度计算。钉根部的抗弯强度计算公式和钉端部的挠度计算公式，涉及工艺参数包括挂钉高度、挂钉受力和挂钉材料弹性模量。

挂钉受力：挂钉受力P由进挂钉纤维张力F1=F、出挂钉纤维张力F2=F、进入挂钉前的缠绕角α1=α、离开挂钉后缠绕角α=90决定。在零度缠绕工艺特殊情况下，纤维轨迹在筒件端部经过挂钉时，在停留角度过小情况下将直接绕钉返回，此时挂钉受力为2倍纤维张力2F，挂钉受力分析如图10所示。

挂钉受力公式为：

P=F21+F22+2F1F2cos（90-α）

F1=F1F2=FP=F2+2cos（90-α）（6）

抗弯强度：挂钉的最大正应力发生在最大弯距的横截面上距中性轴最远的各点处，而此处的切应力等于零。即挂钉的最大工作正应力σmax不得超过材料的许用屈服强度［σs］，否则挂钉将发生塑性变形，其抗屈塑性条件为：

MmaxWy≤［σs］

Mmax=Pl32plπd3≤［σs］d3≥32plπ［σs］（7）

公式（7）为挂钉直径抗弯公式，式中Mmax为挂钉最大弯距，Wy为挂钉圆形截面抗弯截面系数，［σs］为材料许用屈服强度（45号钢的屈服强度大致为355 MPa），P为挂钉端部的垂直力，l为挂钉高度，d为挂钉直径。

挠度控制：本文提出最大挠度钉径比概念，以可接受的挂钉端部最大挠度钉径比y %=50 %为落纱点偏移尺度，进行挂钉直径校核。

yE=Pl33EI

I=πd464y5=64Pl33πEd4

d4=642πE×Pl3yE

yE=d×y %y %=649πE·dE×Pl3（8）

公式（8）为挂钉端部挠度公式，式中yE为挂钉端部的最大挠度，P为挂钉端部的垂直力，l为挂钉高度，E为材料弹性模量，l为挂钉圆形截面惯性距，d为挂钉直径，y %为挂钉端部的最大挠度钉径比。

挂钉间距：当挂钉直径满足抗弯强度和挠度控制，则挂钉间距公式为：

△L=yE+d+bp1.5d+bp（9）

公式（9）为挂钉间距公式，式中△L为挂钉环向距离，yE为挂钉端部的最大挠度，d为挂钉直径，bp为工艺落纱宽度。

3结语

结合纤维缠绕理论和仿真技术，给出圆管类纤维缠绕转长直径比kL经验公式kL=12f|cscα-1|，转长直径比kL只与纤维层间摩擦系数f和圆筒段缠绕角度有关，转长直径比是缠绕角余割的一元一次方程。

基于转向区长度计算公式，提出的转长直径比概念，预定kL=1为临界转长直径比，此时缠绕角近似等于54.7°。随后，根据缠绕制品的实际缠绕角，规划出圆管类纤维缠绕工艺的三条技术路线（传统圆管缠绕工艺、柱面转向挂钉工艺、端面转向挂钉工艺）。当实际缠绕角α≥54.7°时，转长直径比近似等于1，此时纤维缠绕圆管工艺路线选择传统圆管缠绕工艺，可以应用实际摩擦系数且可控制合理转向长度。当实际缠绕角α＜54.7°时，控制转长直径比kL=1，控制纤维轨迹在端面转向，摩擦系数设置等于实际，宜采用端面转向挂钉工艺。当实际缠绕角α＜54.7°时，控制转长直径比kL=1，控制纤维轨迹在柱面转向，摩擦系数设置大于实际，宜采用柱面转向挂钉工艺。

参 考 文 献

［1］遇家运，刘佳.复合材料圆管成型工艺及性能研究现状［J］.纤维复合材料，2022，39（01）：82-86.

［2］刘永，南洋，许华明.国内连续缠绕玻璃钢管技术专利分析［J］.纤维复合材料，2020，37（04）：128-132.

［3］郭文强，李国树.纤维缠绕玻璃钢管道端部的缠绕规律［J］.纤维复合材料，2005，（01）：45-46.

［4］冷兴武.纤维缠绕原理［M］.山东科学技术出版社，1990：121-122.

［5］赫晓东，王荣国，矫维成，等.先进复合材料压力容器［M］.科学出版社，2016：76-79.