基于群体平衡的胶凝原油水力悬浮体系流动特性模拟

孙省身 侯磊 杨琨 刘珈铨 张鑫儒 朱祚良 唐帅帅 周庆林

摘要：胶凝原油水力悬浮体系流动特性研究是高含水油田实现不加热集输的关键。近年来随着计算流体力学的发展，数值模拟成为复杂流体流动特性研究的有效工具。根据群体平衡模型，引入关键的凝油颗粒碰撞聚并与剪切破碎函数，描述颗粒群间的相互作用，在三维管道模型下求解，通过文献试验数据对模拟结果进行验证。结果表明：随着流速或含水率的增加，凝油颗粒平均粒径减小，粒径呈圆环状分布，油相分布更加均匀，不易产生凝油壁面沉积；在高含水阶段，流速增大对流动压降增大的影响占主导地位，含水率的影响不明显，颗粒粒径减小或凝油沉积也会导致流动压降增大。

关键词：胶凝原油； 群体平衡模型； 碰撞聚并； 剪切破碎； 流动特性

中图分类号：TE 832    文献标志码：A

文章编号：1673-5005（2024）03-0162-08   doi：10.3969/j.issn.1673-5005.2024.03.018

Simulation of flow characteristics of hydraulic suspension system of gelled crude oil based on population balance

SUN Xingshen1， HOU Lei1， YANG Kun2， LIU Jiaquan1， ZHANG Xinru1， ZHU Zuoliang1， TANG Shuaishuai1， ZHOU Qinglin2

（1. College of Mechanical and Transportation Engineering/MOE Key Laboratory of Petroleum Engineering， China University of Petroleum （Beijing）， Beijing 102249，China;2.China Liaohe Petroleum Engineering Company Limited， Panjin 124010， China）

Abstract： The study on the flow characteristics of hydraulic suspension system of gelled crude oil is the key to realize unheated gathering and transportation in high water cut oilfield. In recent years， with the development of computational fluid dynamics， numerical simulation has become an effective tool to study the flow characteristics of complex fluids. Based on the population balance model， the key gelled oil particle collision aggregation and shear breakage functions were introduced to describe the interaction among particle groups. The solution was obtained under the three-dimensional pipeline model and the simulation results were verified by experimental data in the literature. The results show that with the increase of flow rate or water cut， the mean diameter of gelled oil particles decreases， the particle diameter takes a circular distribution， and the distribution of oil phase is more uniform， which is not easy to cause gelled oil wall deposition. In the high water cut stage， the influence of flow rate increasing on the increase of flow pressure drop is dominant， but the influence of water cut is not obvious. The decrease of particle diameter or gelled oil deposition can also lead to an increase in flow pressure drop.

Keywords： gelled crude oil; population balance model; collision aggregation; shear breakage; flow characteristics

不加热集输工艺被广泛应用于开发中后期的油田集输管道，显著降低地面集输系统的能耗，提升油田的经济效益［1-2］。此类管道流动具有高含水、低温的特点，处于胶凝原油水力悬浮输送体系，易产生“凝油粘壁”等管道流动安全保障问题［3-4］。在水力悬浮输送过程中，凝油颗粒粒径分布及油相体积分数分布对油水混合液的当量黏度与流动压降产生重要影响。目前冷指搅拌槽［2］与环道［3］被用于主要研究两相流动规律。但采用试验方法研究流动中颗粒相分布规律所需的条件非常苛刻，且成本较高［5］。近年来，随着计算流体力学（CFD）的发展，数值模拟成为复杂流体流动特性研究的有效工具［6-8］。Helenbrook等［9］利用有限元方法求解不同液滴的变形行为及阻力预测模型。赵辰辰［10］针对单颗粒运动进行模拟，修正了胶凝油团水力悬浮的曳力系数。刘晓燕等［11］针对胶凝原油水力悬浮输送这一特殊的两相流体系，采用离散相模型得到了单个凝油颗粒运动规律与变形特征。但是，前人的研究主要停留在管道内单个凝油颗粒运动轨迹追踪与受力变形的分析，颗粒群相互作用的数值模拟研究未见报道。其次，目前已有数值模拟的物理模型大多为二维的矩形模拟区域，不能满足实际管道的复杂流动状况。胶凝原油水力悬浮流动的数值模拟研究亟待从二维矩形流场发展到三维实际管道，从单颗粒模拟深化到颗粒群的模拟。针对以上数值模型存在的问题，笔者根据群体平衡模型，引入关键的凝油颗粒碰撞聚并与剪切破碎函数，描述颗粒群间的相互作用；在三维管道模型下求解，研究流速与含水率对凝油颗粒粒径分布、油相体积分数分布及流动压降等流动特性的影响。

1 数值模型

1.1 控制方程

本模拟所涉及控制方程主要包括油水两相流模型、连续相水的湍流模型、胶凝原油颗粒与水的液固耦合模型及颗粒间相互作用的群体平衡模型。

1.1.1 两相流模型及湍流模型

采用欧拉双流体模型描述胶凝原油-水两相流动，水为连续相，胶凝原油颗粒为离散相，选择标准k-ε湍流模型描述水力悬浮流动，运动方程主要包括连续性方程和动量方程，其中连续相和离散相的动量方程分别为

（ρlφlul）t+·（ρlφlulul）=-φlpl+φlρlg+·τl+M.（1）

（ρsφsus）t+·（ρsφsusus）=-φsps+φsρsg+·τs+M.（2）

式中，ρl和ρs分别为水相（连续相）、油颗粒相（离散相）的密度，kg·m-3；φl、φs分别为水相、油颗粒相的体积分数；ul和us分别为水相、油颗粒相的速度，m·s-1；t为流动时间，s；pl和ps分别为水相、油颗粒相的分压，Pa；g为重力加速度，m·s-2；τl和τs分别为水相、油颗粒相的应力张量，Pa；M为相间作用力，kg·m-2·s-2。

1.1.2 液固耦合模型

颗粒运动变形的本质是颗粒所受作用力的行为史。颗粒所受作用力主要包括油颗粒与水之间的液固耦合以及颗粒群之间的相互作用。液固耦合主要在于计算相间作用力（M），本模拟主要考虑颗粒所受作用力为相间曳力（Md）和湍流弥散力（Mt）。

采用Simonin模型［12］计算湍流弥散力，采用刘晓燕等［13］修正后的胶凝原油曳力系数模型计算相间曳力，表示为

Mt=ksl·μmρmσdφsφs-φlφl.（3）

Md=ksl（u1-us）=34CDρ1（u1-us）2ρsL .（4）

其中

CD=0.53+24μl8n-1ρlDnum2-n4n3n+1n·1+4.56φ0.73s1-φs.

式中，ksl为流固交换系数，kg·m-3·s-1；μm为混合物当量黏度，kg·m-1·s-1；ρm为混合物密度，kg·m-3；σd为普朗克扩散系数；d为油颗粒粒径，m；CD为曳力系数；n为油的流动行为指数；um为油水混合物的速度，m·s-1；μl为水相黏度，kg·m-1·s-1；D为管道内径，m。

根据式（4）编制UDF计算曳力模型。

1.1.3 群体平衡模型

许多研究者将群体平衡模型应用于分散体系内气泡、液滴、颗粒等破碎和聚并的过程［14-16］。群体平衡模型包含颗粒演化过程的许多现象，如成核、生长、分散、溶解、聚集和破碎，用于描述不同粒径的粒子数变化。根据颗粒碰撞聚集与剪切破碎对胶凝原油颗粒数量密度的关系，建立群体平衡模型为

n（V，t）t=12∫V0λh

（V-V′，V′）n（V-V′，t）n（V′，t）dV′聚集导致颗粒生成-

∫0λh（V，V′）n（V，t）n（V′，t）dV′聚集导致颗粒消亡+

∫Vβ（V|V′）g（V′）n（V′，t）dV′破碎导致颗粒生成-g（V）n（V，t）破碎导致颗粒消亡 .（5）

式中，V为凝油颗粒的体积，m3；n（V，t）为t时刻体积V的凝油颗粒的数量密度，m-3；λ为凝油颗粒的聚并效率；h（V，V′）为体积V和V′的凝油颗粒间的碰撞频率，s-1；β（V|V′）为体积V′的凝油颗粒破碎形成子颗粒的分布，m-3；g（V）为体积V的凝油颗粒的破碎频率，s-1。

在碰撞频率方面，主要考虑差速沉降和流动剪切效应，取两者的碰撞频率之和作为凝油颗粒的实际碰撞频率，其中差速沉降频率（hDS）采用Camp［17］模型进行计算。由于凝油颗粒粒径为毫米级，大于Kolmogorov尺度［16］，处于惯性子区，比最小涡流大，因此流动剪切频率（hST）主要受流场中速度波动的作用，采用Abrahamson［18］模型进行计算，表示为

hDS（Li，Lj）=π4（Li+Lj）2Si-Sj.（6）

其中

S=347.5602L1.54，hST（Li，Lj）=232π（Li+Lj）24u2i+u2j .

式中，S为颗粒的沉降速率，m·s-1；u为颗粒的平均速度，m·s-1。

在聚并效率方面，主要考虑颗粒间聚并作用的范德华力与破碎作用的流动剪切力之比，采用Ven模型［19］进行计算，表示为

λ=a（H/36πμ1R3）0.18 .（7）

式中，a为与流体性质有关的常数；H为Hamaker常数；R为两个油颗粒的调和半径，m;为流场剪切速率，s-1。

在破碎频率方面，主要考虑流动剪切效应导致的颗粒破碎，破碎频率与剪切率和颗粒粒径呈正相关［20］，表示为

g（V）=EmL.（8）

式中，E和m为经验常数。

在子颗粒粒径分布方面，采用二元破碎描述子颗粒的分布情况，表示为

β（V′-V|V′）=β（V|V′）.（9）

根据式（6）～（8）编制UDF计算碰撞破碎函数。

1.2 基本假设

在建模过程中，做出如下假设，简化数值模型：

（1）不考虑能量方程，认为流动是一个等温过程；

（2）对于群体平衡模型只考虑颗粒的聚集与破碎过程，忽略颗粒的成核、生长、溶解以及颗粒在管壁上的黏附过程；

（3）对于流动介质只考虑水相和凝油颗粒相，不考虑气相；

（4）认为颗粒粒径是一个连续的分布函数。

1.3 边界条件与网格划分

以范伟［5］开展的试验为模拟对象，采用Fluent 2020r1软件对控制方程联合求解，并将模拟结果与试验结果进行对比。以水平直管段（长度为1 m，内径为53 mm）为几何模型，进行六面体网格划分，网格划分步长为1 mm。为处理边界层效应，在近壁面处采用8层网格加密，划分后的网格如图1所示。管道边界条件为速度入口，压力出口。使用二阶迎风格式离散动量方程，使用SIMPLE算法求解压力-速度耦合问题，使用离散法求解群体平衡方程。残差设置为10-5，模拟迭代至流动压降不再显著变化时结束计算。对网格数为269120和380600的结果进行比较，管流径向流速平均误差小于5%，认为269120个网格能满足网格无关性要求。

1.4 模型参数

模型求解时水相、油相密度分别取1000和890 kg/m3；水相、油相黏度分别取0.00179和4 Pa·s；聚并效率常数a取0.87［20］；Hamaker常数H取6.4×10-21 J［21］；破碎频率经验常数E、m分别取700 s0.15·m-1和1.15［22］。

2 模拟结果

2.1 模拟工况

设置10种工况（表1）研究流速（工况4～7）及含水率（工况7～10）对胶凝原油颗粒粒径分布、油相体积分数分布及流动压降等流动特性的影响。其中工况1～3的流速和含水率与文献［5］中试验工况相同，用于对比模拟结果与试验结果。此外，在使用群体平衡模型时，需要给出油颗粒初始粒径分布。在文献［5］试验中，胶凝原油首先被流态化处理［11］，使其被垂直水流冲击剪切，形成较规整的颗粒。为便于模拟的对比性，初始粒径取流态化处理装置多孔喷嘴的直径，即油颗粒初始粒径均为1 mm。

2.2 模型验证

工程1～3中压降梯度的对比结果见表2。试验值和模拟值的压降梯度变化趋势相同，相对误差小于11%，说明所建模型反映胶凝原油水力悬浮流动压降规律的可行性。

3种工况下试验和模拟的粒径分布如图2所示。由图2可知，模拟与试验得到的粒径变化趋势相近。相较于正态分布，模拟的粒径分布规律更接近于对数正态分布，与试验规律相同［5］。此外，在部分粒径区间内分布误差可达10%。这一方面是因为试验取样随机、不连续，造成粒径分布情况与实际管道有出入；另一方面，大部分粒径变化是微米级的，模拟时设置更小的粒径观测区间，所得的颗粒粒径分布精度会更高。

2.3 流速对流动特性的影响

2.3.1 流速对颗粒粒径分布的影响

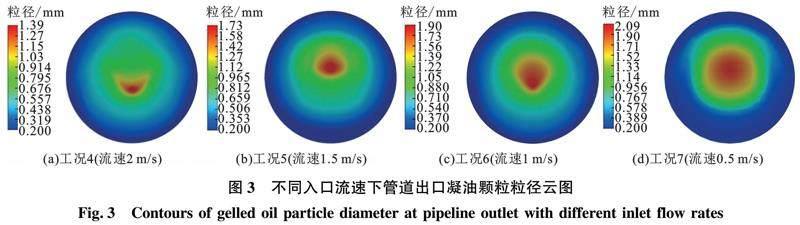
平均粒径、最小粒径和最大粒径是最常用的特征粒径参数。工况4～7的颗粒特征粒径如表3所示。随着流速增大，胶凝原油颗粒的特征粒径均减小，最大粒径从2.09 mm变化至 1.39 mm，粒径减小的幅度大于平均粒径。小颗粒（粒径小于0.4 mm）所占比例逐渐增大，大颗粒（粒径大于1 mm）所占比例逐渐减小。根据颗粒碰撞理论可知，流速的增加带来相反两方面的影响：一方面连续相对分散颗粒相的剪切破碎作用增强；另一方面，湍流作用的增强增大了颗粒的碰撞聚集概率。这表明在本模拟工况的参数范围内，流速增大对颗粒的剪切破碎占主导作用，使颗粒粒径分布整体向较小粒径方向偏移，这与范伟［5］试验所得的颗粒粒径特性相同。而剪切破碎频率与粒径呈正相关，在粒径接近最大临界值时，受到剪切作用更容易破碎形成较小颗粒，小颗粒则相对稳定，从而造成流速的变化对最大粒径的影响大于平均粒径。此外，由于在群体平衡模型设置初始分布时须指定最小粒径（本文为0.2 mm），因此在最小粒径方面未能体现上述变化。

在颗粒粒径分布函数方面，最常用的3种分布函数为Normal分布、Log-Normal分布和Rosin-Rammler分布。按照这3种分布函数对模拟结果进行拟合，拟合优度R2见表3。Log-Normal分布与Rosin-Rammler分布的拟合优度R2均超过0.9，两者均能较好地描述管道中胶凝原油颗粒的分布类型，Normal分布的拟合效果则较差，这与范伟［5］、吕宇玲［22］研究结果相一致。

管道出口截面凝油颗粒分布如图3所示。由图3可知，管道截面上颗粒粒径呈现圆环状分布，越靠近壁面处粒径越小。结合粒径特性分析可知，管流剪切率从管壁向管道中心依次递减，管壁处剪切率最大，因此颗粒最容易被剪切成小颗粒。

2.3.2 流速对油相体积分数分布影响

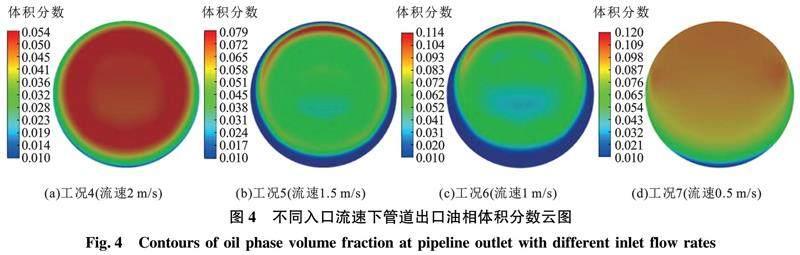
工况4～7的管道出口油相体积分数如图4所示。由图4可知，随着流速增加，管道中固液相流型由分层流（工况7）转变为分散流（工况4～6）。在工况7中管道流速较低，由于胶凝原油密度小于水，凝油颗粒会迅速上浮并在管道顶部形成聚集层，聚集层内油相体积分数高于10%，而在管道底部形成低分布区，体积分数小于2%，且油相体积分数从顶部向底部依次递减，形成分层流型。

在工况4～6中，管道中心体积分数较均匀，近壁面体积分数低，形成分散流流型。这是因为近壁面处流速低于管道中心，流速越高，湍流弥散力越大，使得颗粒能够在管道中心弥散均匀。此外随流速增大，管道顶部聚集层体积分数峰值从11.4%递减为5.4%，管道中心处颗粒分布更加均匀。这也说明高流速下连续相水对凝油颗粒的携带和弥散作用更强，使分散相颗粒不易聚集沉积在管道上部，更容易形成分散流型。

2.3.3 流速对压降梯度和当量黏度影响

工程中对于非均匀油水混合物在管道内的流动，往往将混合物看成均匀的单相流体，通过流动压降反算混合物的当量黏度，以描述油水混合液的流动特性。

工况4～7下，压降梯度（dp/dz）与当量黏度（μm）随流速的变化如图5所示。由图5可知，随着流速增大，压降梯度增大，且压降梯度的增幅也逐渐增大。而油水混合液的当量黏度随流速从0.5 m/s变化至1.0 m/s时显著减小，随流速从1.0 m/s变化至2.0 m/s时小幅增大。结合图3粒径分布变化可知，颗粒粒径分布和数量也会对混合物的压降梯度和当量黏度产生一定影响。流速增大使得颗粒整体向较小粒径方向偏移，小颗粒数量增加使得油水相界面浓度和界面能增大，引起相间摩擦力增大，从而导致混合物的当量黏度随流速从1.0 m/s变化至2.0 m/s时小幅增大。同时，相间摩阻的增大也带来了额外的一部分压降损失，引起压降梯度的增幅随流速增大而增大。

此外，结合图4可以发现，从工况7变化到工况6时，管道中流型从分层流转变为分散流，分散相颗粒朝着管道中心均匀分散，减小了管道顶部聚集区的油相体积分数，颗粒之间的摩擦力减小从而导致当量黏度显著减小。

2.4 含水率对流动特性影响

2.4.1 含水率对颗粒粒径分布影响

工况7～10的颗粒特征粒径如表4所示。随着含水率的升高，胶凝原油颗粒的特征粒径均减小，最大粒径从2.81 mm变化至2.09 mm，粒径减小的幅度大于平均粒径。小颗粒（粒径小于0.4 mm）所占比例逐渐增大，大颗粒（粒径大于1 mm）所占比例逐渐减小。这是因为含水率的升高使得分散油相的碰撞概率减小，颗粒的碰撞聚并效应减弱，粒径整体减小。而颗粒碰撞聚集的概率与颗粒粒径呈正相关，大粒径颗粒受到聚并作用的削弱影响更大，较小粒径颗粒则相对稳定。同样，由于在模拟中指定初始粒径分布时设定了最小粒径（0.2 mm），因此在最小粒径方面未能体现上述变化。

在颗粒粒径分布函数方面，3种分布函数的拟合结果见表4。凝油颗粒粒径同样较好地符合Log-Normal分布与Rosin-Rammler分布。

管道出口截面凝油颗粒分布如图6所示。由图6可知，在不同的含水率下管道截面上颗粒粒径同样呈现圆环状分布，越靠近壁面处粒径越小，其原因与图3粒径云图的结果相一致。

2.4.2 含水率对油相体积分数分布影响

工况7～10的管道出口油相体积分数如图7所示。由图7可知，当管内处于高含水低流速工况时，管内流型均为分层流。随着含水率升高，管道上部聚集层的体积分数峰值从22.4%降低至12%，且聚集层的范围越来越小。这表明在相同的流速下，含水率越高，分散相颗粒聚集沉积的概率越低，更容易在管道中分散。但是，流速和含水率共同影响着颗粒相的分布，相较于含水率，流速的影响占主导地位，使得含水率的变化对两相流型的改变不明显。因此在低流速高含水率工况下，管内流型仍然为分层流。

2.4.3 含水率对压降梯度和当量黏度影响

工况7～10下，压降梯度与当量黏度随含水率的变化见图8。由图8可知，在高含水阶段（含水率80%～95%），随着含水率减小，压降梯度与当量黏度均逐渐增大，且变化趋势较为一致。含水率减小引起压降梯度变化的幅值小于100 Pa·m-1，远小于流速的影响（图5）。此时，混合液的当量黏度虽小幅上升，但是仍远低于油相的黏度（4 Pa·s）。这是因为在高含水阶段，水是连续相，油是分散相，连续相的黏度是影响压降变化的关键因素，而分散相的黏度对其影响不大。随着含水率变化，分散相颗粒数量和分布的变化使得压降小幅变化，但颗粒数量及其分布在高含水阶段对压降的影响并不明显。

3 结 论

（1）随着流速或含水率增加，凝油颗粒平均粒径减小，油相体积分数分布更加均匀，更容易形成分散流型，不易产生凝油壁面沉积。

（2）管道截面上颗粒粒径呈现圆环状分布，越靠近壁面处粒径越小，通过Log-Normal分布和Rosin-Rammler分布均能较好地描述粒径分布规律。

（3）在高含水阶段，流速增大对流动压降增大的影响占主导地位，含水率的影响不明显，颗粒粒径减小或凝油沉积也会导致流动压降的小幅增大。

建议未来研究凝油颗粒壁面黏附模型，将其与群体平衡模型耦合求解，进一步揭示胶凝原油在管道内的沉积演化机制。

参考文献：

［1］ 刘晓燕，王德喜，韩国有，等.特高含水采油期安全混输温度界限试验研究［J］.石油学报，2005，26（3）：102-105.

LIU Xiaoyan， WANG Dexi， HAN Guoyou， et al. Temperature limit for oil-gas-water mixed transportation in safety during oil production with special high water-cut［J］. Acta Petrolei Sinica， 2005，26（3）：102-105.

［2］ 韩善鹏，贾治渊，赵芸黎，等.板北油田不加热集油问题研究［J］.北京石油化工学院学报，2018，26（2）：56-60.

HAN Shanpeng， JIA Zhiyuan， ZHAO Yunli， et al. Study of gathering pipelines unheated operation in Banbei Oilfield［J］. Journal of Beijing Institute of Petrochemical Technology， 2018，26（2）：56-60.

［3］ ZHENG H， HUANG Q， WANG C. Wall sticking of high water-cut crude oil transported at temperatures below the gel point［J］. Journal of Geophysics and Engineering， 2015，12（6）：1008-1014.

［4］ 吕杨，朱国承，霍富永，等.不加热集油粘壁规律研究进展［J］.化工进展，2020，39（2）：478-488.

L Yang， ZHU Guocheng， HUO Fuyong， et al. Research progress on wall sticking of gelled crude oil at low-temperature transportation［J］. Chemical Industry and Engineering Progress， 2020，39（2）：478-488.

［5］ 范伟.胶凝原油水力悬浮多相流动特性研究［D］.大庆：东北石油大学，2014.

FAN Wei. Study on hydraulic suspension conveying multiphase flow characteristics of gelled crude oil［D］. Daqing：Northeast Petroleum University， 2014.

［6］ 蔡禄，武晓波，孙治谦，等.双蜗壳旋流器内部流场及液膜特性的数值模拟［J］.石油机械，2022，50（10）：111-118.

CAI Lu， WU Xiaobo， SUN Zhiqian， et al. Numericalsimulation on internal flow field and liquid film characteristics of double volute cyclone［J］. China Petroleum Machinery， 2022，50（10）：111-118.

［7］ 雷玲卷，张兴凯，廖锐全，等.基于强制环状流工况的湿气测量数值模拟研究［J］.石油机械，2022，50（10）：87-95.

LEI Lingjuan， ZHANG Xingkai， LIAO Ruiquan， et al. Numerical simulation of wet gas measurement under forced annular flow conditions［J］. China Petroleum Machinery， 2022，50（10）：87-95.

［8］ 朱军龙，李清平，秦蕊，等.水下油嘴多相节流温降数值模拟及规律研究［J］.石油机械，2022，50（6）：65-71.

ZHU Junlong， LI Qingping， QIN Rui， et al. Numericalsimulation and regularity study for throttling temperature drop of multiphase flow through subsea chokes［J］. China Petroleum Machinery， 2022，50（6）：65-71.

［9］ HELENBROOK B T， EDWARDS C F. Quasi-steady deformation and drag of uncontaminated liquid drops［J］. International Journal of Multiphase Flow， 2002，28（10）：1631-1657.

［10］ 赵辰辰.单颗粒胶凝原油水力悬浮输送的数值模拟研究［D］.大庆：东北石油大学，2014.

ZHAO Chenchen. Numerical simulation research on single suspension conveying gelled crude oil［D］. Daqing：Northeast Petroleum University， 2014.

［11］ 刘晓燕，李友行，李晓庆，等.胶凝原油颗粒变形的数值模拟研究［J］.工程热物理学报，2015，36（3）：551-554.

LIU Xiaoyan， LI Youxing， LI Xiaoqing， et al. Numericalsimulation study on the deformation of the gelled crude oil particle［J］. Journal of Engineering Thermophysics， 2015，36（3）：551-554.

［12］ SIMONIN O， VIOLLET P L. Modelling of turbulent two-phase jets loaded with discrete particles［J］. Phenomena in Multiphase Flows， 1990：259-269.

［13］ LIU X， ZHAO C， LI X， et al. Study on drag coefficient of gelled crude oil particles［J］. American Journal of Heat and Mass Transfer， 2014，1（1）：24-29.

［14］ 王铁峰.气液（浆）反应器流体力学行为的实验研究和数值模拟［D］.北京：清华大学，2004.

WANG Tiefeng. Experimental study and numerical simulation on the hydrodynamics in gas-liquid （slurry） reactors［D］. Beijing：Tsinghua University， 2004.

［15］ 宋光春，李玉星，王武昌，等.基于群体平衡理论的水合物聚集动力学模型［J］.化工进展，2018，37（1）：80-87.

SONG Guangchun， LI Yuxing， WANG Wuchang， et al. A research on the dynamic model of hydrate agglomeration based on population balance theory［J］. Chemical Industry and Engineering Progress， 2018，37（1）：80-87.

［16］ 于水波.湍流液-液分散体系中液滴聚并过程的研究［D］.大连：大连理工大学， 2008.

YU Shuibo. The study of drop coalescence in the liquid-liquid turbulent dispersions［D］. Dalian： Dalian University of Technology， 2008.

［17］ CAMP T R. Velocity gradients and internal work in fluid motion［J］. Journal of the Boston Society of Civil Engineers， 1943，30：219-230.

［18］ ABRAHAMSON J. Collision rates of small particles in a vigorously turbulent fluid［J］. Chemical Engineering Science， 1975，30（11）：1371-1379.

［19］ VEN T G M， MASON S G. The microrheology of colloidal dispersions［J］. Colloid and Polymer Science， 1977，255（8）：794-804.

［20］ BALAKIN B V， HOFFMANN A C， KOSINSKI P. Population balance model for nucleation， growth， aggregation， and breakage of hydrate particles in turbulent flow［J］. AIChE Journal， 2010，56（8）：2052-2062.

［21］ ZHANG Y， HUANG Q， CUI Y， et al. Estimating wall sticking occurrence temperature based on adhesion force theory［J］. Journal of Petroleum Science and Engineering， 2020，187：106778.

［22］ 吕宇玲.油水两相分散流的液滴特征与压降规律研究［D］.青岛：中国石油大学（华东），2012.

L Yuling. Investigation of droplet characteristics and pressure drop in oil-water dispersed flows［D］. Qingdao：China University of Petroleum （East China）， 2012.

（编辑 沈玉英）

基金项目：国家自然科学基金项目（51974335）

第一作者：孙省身（1998- ），男，博士研究生，研究方向为高含水原油不加热集输流动安全保障。E-mail： 530045141@qq.com。

通信作者：侯磊（1966- ），男，教授，博士，博士生导师，研究方向为油气田集输理论与技术。E-mail： houleicupbj@126.com。

引用格式：孙省身，侯磊，杨琨，等.基于群体平衡的胶凝原油水力悬浮体系流动特性模拟［J］.中国石油大学学报（自然科学版），2024，48（3）：162-169.

SUN Xingshen， HOU Lei， YANG Kun， et al. Simulation of flow characteristics of hydraulic suspension system of gelled crude oil based on population balance［J］. Journal of China University of Petroleum （Edition of Natural Science），2024，48（3）：162-169.