径向井辅助前置液酸压裂缝扩展数值模拟

齐宁 甘俊冲 章泽辉 刘毅龙 申玉洋 刘练

摘要：基于扩展有限元及双尺度连续模型理论建立径向井辅助前置液酸压裂缝扩展模型，引入偏离系数作为量化评价指标，分析各因素对裂缝形态的影响，并利用灰色关联分析方法明确主控因素。结果表明：径向井对前置液酸压裂缝扩展具有显著引导作用，裂缝优先沿径向井方向起裂并扩展一定距离，而后逐渐偏向最大水平主应力方向；径向井方位角、水平地应力差和地层弹性模量越小，径向井长度越长，偏离系数越小，径向井引导效果越好，其中水平地应力差为主控因素；当径向井方位角为15°时，前置液酸压裂缝沿着径向井方向扩展14.32 m后偏向最大水平主应力方向，径向井的引导效果最好，偏离系数为0.005。

关键词：径向井； 前置液酸压； 裂缝扩展； 扩展有限元； 双尺度模型

中图分类号：TE 357.2   文献标志码：A

文章编号：1673-5005（2024）03-00101-10   doi：10.3969/j.issn.1673-5005.2024.03.011

Numerical simulation of fracture propagation guided by radial well assisted preflush acid fracturing

QI Ning1， GAN Junchong2， ZHANG Zehui1， LIU Yilong1， SHEN Yuyang1， LIU Lian3

（1.School of Petroleum Engineering in China University of Petroleum（East China）， Qingdao 266580， China;2.Natural Gas Evaluation Project Department， PetroChina Changqing Oilfield Company， Xian 710018， China；3.Northwest Oilfield Company， SINOPEC， Urumqi 830011， China）

Abstract：In this paper， a fracture propagation model of radial well assisted preflush acid fracturing was established based on the extended finite element method and the two-scale continuum model theory. The term "deflection factor" was introduced as the quantification criterion to analyze the influence of various factors on the fracture morphology， and the main control factors were identified by using the gray correlation analysis method. The simulation results show that the radial well has a significant guiding effect on the fracture propagation of the preflush acid fracturing. The fracture starts and expands for a certain distance along the radial well， and then gradually deflects to the direction of the maximum horizontal principal stress. Smaller azimuth of the radial well， horizontal in-situ stress difference and elastic modulus of rock and longer length of the radial well can cause smaller deflection factor and better guiding effect. The most important influence factor is the horizontal in-situ stress difference. For instance， when the azimuth of the radial well is 15°， the fracture can propagate 14.32 m along the radial well， and deflect to the direction of the maximum principal stress finally. In this case， the radial well has the best guiding effect， and the deflection factor is 0.005.

Keywords：radial well; preflush acid fracturing; fracture propagation; extended finite element method; two-scale continuum model

前置液酸压技术是碳酸盐岩储层常用的改造技术之一，其多形成沿最大主应力方向扩展的平直裂缝［1］，而传统平直裂缝难以有效沟通油气储集体［2］。通过径向井技术［3-4］与前置液酸压技术的联合［5］，可有效改变周围地层应力状态，使酸压裂缝偏离最大主应力方向定向扩展，从而达到沟通非主应力方向油气储集体［6］、提高油气藏动用程度的目的［7］。鲜保安等［8］、Megorden等［9］基于现场试验提出并验证了径向井压裂技术，可有效引导水力裂缝定向扩展，提高储层动用程度［10-13］。薛衡等［14-16］将前置液酸压解耦为前置液造缝与酸液溶蚀过程，研究了非均质性和多重滤失效应的影响。上述学者主要针对径向井水力裂缝扩展和常规前置液酸压数值模拟研究，但前置液酸压沟通非主应力方向储集体的研究尚未见报道，而径向井引导酸压裂缝定向扩展需要考虑复杂的酸岩反应。笔者基于双尺度连续模型理论建立酸液溶蚀模型，采用径向井压裂模型模拟前置液造缝过程，针对不同地质因素（水平地应力差、地层弹性模量）和工艺因素（径向井方位角、径向井长度）等开展数值模拟研究，并分析裂缝扩展的主控因素，为径向井辅助前置液酸压技术的现场应用提供理论依据。

1 径向井辅助前置液酸压模型建立

1.1 前置液造缝模型

前置液造缝是指将非反应性流体注入地层，压开地层形成裂缝的过程，该部分为后续酸液溶蚀提供了裂缝几何尺寸，从而提高前置液酸压全过程模拟的准确性。为求解该过程，假设：①地层饱和不可压缩流体；②前置液流动过程中不会发生酸岩反应；③地层岩石均质，地层中不存在天然裂缝。

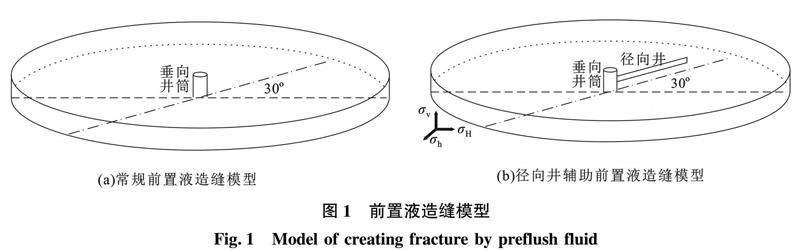
前置液造缝与水力压裂的本质相同，基于径向井辅助水力压裂数值模型，采用Abaqus软件建模并划分网格，模拟水力压裂过程中的流固耦合效应，并采用扩展有限元方法模拟裂缝起裂及扩展过程，建立常规前置液造缝模型和30°方位角径向井辅助前置液造缝模型（图1），模拟前置液造缝过程中的裂缝形态变化，并以裂缝几何尺寸为基础开展后续酸液溶蚀模拟。

前置液造缝模型的初始条件为

p=p0， φ=φ0， Ux=0， Uy=0， Uz=0.

边界条件为

Ux=0， Uy=0， q=qqzy， R=R1;p=p0， Ux=0， Uy=0， Uz=0， R=Rmax.

式中，p为压力，Pa；φ为孔隙度；q为注入速度，m3/s；R为距模型中心的距离，m；Ux、Uy、Uz分别为最大水平主应力、最小水平主应力、垂向应力方向上的位移，m；φ0为岩石初始孔隙度；R1为垂向井筒半径，m；Rmax为模拟地层半径，m；qqzy为前置液注入速度，m3/s；p0为原始地层压力，Pa。

油藏地质参数：垂向应力为45 MPa，最大水平主应力为41 MPa，最小水平主应力为38 MPa，原始孔隙压力为20 MPa；试验测得岩石物性参数：岩石泊松比为0.25，岩石密度为2.9×103 kg/m3，岩石孔隙度为0.2，岩石渗透率为120 μm2，岩石初始比表面积为1×104 m2/m3，岩石初始孔隙半径为5 μm，岩石滤失系数为1×10-9 m/s；试验测得前置液与酸液物性参数：前置液黏度为0.05 Pa·s，酸液初始浓度为4.41 mol/L，酸液密度为1.1×103 kg/m3，酸液黏度为2 mPa·s，酸溶蚀能力为0.05 kg/mol；其他模型设定值：计算域直径为40 m，套管直径为0.14 m，径向井直径为0.03 m，径向井长度为15 m，前置液排量为0.05 m3/s，前置液注入时间为600 s，酸液排量为0.05 m3/s，酸液注入时间为2400 s，岩石抗拉强度为3 MPa，岩石弹性模量为12.9 GPa。

1.2 酸液溶蚀模型

酸液溶蚀模型需以裂缝几何尺寸为基础，对于裂缝贯穿单元，扩展有限元方法利用距离函数

φ（X，t）

描述单元节点到裂缝表面的距离，当研究点X位于裂缝轨迹的下方时，距离函数为负，反之为正（图2）。距离函数的表达式为

φ（X，t）=±minxr∈γ（t）X-Xr.（1）

式中，φ（X，t）为t时刻X节点的距离函数；γ（t）为t时刻的裂缝轨迹；Xr为裂缝轨迹上一点。

对于扩展有限元方法，裂缝尖端只能停留在扩展有限元单元的边界上，可将单个贯穿单元内裂缝近似看作一条直线［17］。由Abaqus前置液造缝模拟结果获取贯穿单元全部结点（图2中1、2、3、4）的距离函数值φ（X，t），计算4个节点之间的距离函数零位置即为裂缝的位置坐标（图2中A、B），遍历所有贯穿单元即可获取前置液造缝部分形成的裂缝几何尺寸。

利用双尺度连续模型模拟高压注入酸液过程中裂缝的动态溶蚀过程和地层物性的动态变化过程。双尺度连续模型耦合了达西尺度模型与孔隙尺度模型，考虑酸液流动与酸岩反应的耦合关系，是酸化酸压领域应用最广泛的数学模型之一［18］。当酸液注入地层后，酸液快速充满地层裂缝区域，酸液中的H+在对流扩展作用下传质到岩石表面发生酸岩反应，从而改变地层物性。为求解该过程，假设：①地层中仅存在一条水力裂缝；②地层内饱和不可压缩流体；③忽略重力和毛细管力的影响。

1.2.1 基质中的达西尺度模型

基质中的酸液流动为多孔介质渗流［19］，采用达西定律控制基质中酸液的径向流流动，采用不可压缩流体连续性方程控制基质中的压力分布，采用对流扩散方程控制酸液消耗，此时酸液不能完全溶蚀岩石，表达式分别为

（u，v）=-kμpsyL，1Lpsyθ，（2）

φt+1LL（Lu）+1Lvθ=0，（3）

（φCf）t+1Lr（LuCf）+1L（vCf）θ+kcav（Cf-Cs）=1LLLφDerCfL+1LθφDeθLCfθ，dφdt=kcav（Cf-Cs）βρ .（4）

式中，L为极径，m；θ为极角，rad；u为r方向上的流速，m/s；v为θ方向上的流速，m/s；k为地层渗透率，m2；μ为酸液黏度，Pa·s；psy为酸液压力，Pa；t为反应时间，s；Cf为酸液浓度，mol/L；D

er和Deθ分别为r和θ方向上的氢离子扩散系数，m2/s；kc为氢离子传质系数，m/s；av为岩石比面，m2/m3；Cs为基质表面的酸液浓度，mol/L；β为单位摩尔酸液所能溶蚀的岩石质量，kg/mol；ρ为岩石密度，kg/m3。

1.2.2 裂缝中的达西尺度模型

裂缝中的酸液流动为N-S方程控制的自由流［19］，利用离散裂缝网络模型［20］对裂缝进行简化从而解决N-S方程与达西方程难以耦合的问题。离散裂缝网络模型将裂缝作为一种特殊的边界条件，并假设在酸液溶蚀过程中，酸液只会增大相邻基质的孔隙度，不会明显改变裂缝形状［21-23］。可采用等效达西定律控制裂缝中酸液的流动［21］，采用不可压缩流体连续性方程控制裂缝中的压力分布，采用对流扩散方程控制酸液消耗，表达式分别为

（u，v）=-k*μpr，1rpθ，（5）

φmaxt+T·V=Qm，（6）

t（φCf）+V·TCf=T·（φDe·TCf）+Sm.（7）

其中

k*=b2/12.

式中，b为裂缝宽度，m；k*为等效渗透率，m2；φmax为裂缝孔隙度，取0.999［21］；T为沿裂缝长度方向的梯度；

V为达西速度矢量，m/s；Qm为裂缝和基质之间的流体交换速度，s-1；De为酸液扩散系数，m2/s；Sm为裂缝和基质之间的氢离子交换速度，mol/（L·s）。

1.2.3 孔隙尺度模型

采用Panga等［18］提出的经验公式控制酸液溶蚀过程中地层孔隙度及渗透率的变化，描述地层在酸液溶蚀过程中的物性变化，

kk0=φφ0φ（1-φ0）φ0（1-φ）2，rpr0=φ（1-φ0）φ0（1-φ） ，ava0=1-φ1-φ0 .（8）

式中，k0为岩石的初始渗透率，m2；rp和r0分别为岩石的孔隙半径和初始孔隙半径，m；a0为岩石的初始比面，m2/m3。

酸液扩散张量取决于孔隙结构、氢离子扩散系数与流动速度，扩散张量可分为r方向

Der与θ方向Deθ［18］，表达式为

Der=（αos+λrPep）Dm，Deθ=（αos+λθPep）Dm.（9）

其中

Pep=2rp/（φDm）V.

式中，αos为与地层孔隙结构相关的常数，取0.5［18］；λr和λθ分别为岩石在r方向和θ方向上孔隙结构系数，均取0.5［18］；Dm为分子扩散系数，m2/s；Pep为佩克莱特数。

酸液传质系数kc取决于流态和孔隙结构，采用舍伍德数Sh［24］计算，

kc=DmSh2rp=Dm2rpSh∞+0.35（2rpRepr）0.5S13c.（10）

其中

Rep=2ρVrp/μ，Sc=μ/（ρDm）.

式中，Rep为孔隙尺度雷诺数；Sc为施密特数；Sh∞为极限舍伍德数，取3.36［24］。

利用COMSOL软件建立酸液溶蚀模型（图3），以前置液造缝部分所得的裂缝几何尺寸作为初始条件，基于双尺度连续模型，利用达西方程模块模拟酸液流动，利用多孔介质稀物质传递模块模拟酸液的对流扩散过程，利用域常微分模块模拟酸岩反应所产生的地层孔隙度和渗透率变化，利用阻力区模拟无限大地层［21］，将以上4个模块耦合，研究多因素对径向井辅助前置液酸压裂缝扩展的影响。

酸液溶蚀模型的初始条件为

p=p0， Cf=0， φ=φ0；

边界条件为

p=pqzy， Cf=C0， q=qsy， R=R1；p=p0， Cf=0， R=Rmax.

式中，pqzy为前置液阶段结束时的井筒压力，Pa；C0为初始酸液浓度，mol/L；qsy为酸液注入速度，m3/s。

2 径向井辅助前置液酸压数值模拟

为明确径向井对前置液酸压裂缝的引导效果，探究不同因素对酸压裂缝扩展的影响，引入偏离系数作为评价径向井引导效果的量化指标。偏离系数是评判径向井引导效果强弱的常用指标之一（又被称为导向因子）［13，25-26］，具有较高的准确性及较强的应用性。偏离系数为以垂直井筒为圆心，裂缝最前端与圆心的连线为半径作引导圆（图4红虚线）。引导圆边界、径向井轴线与裂缝所围面积为S1，引导圆的面积为S，定义偏离系数D为D=S1/S（图4）。偏离系数D的赋值为0～0.25，D越大，反映裂缝偏离径向井轴线越远，径向井的导向效果越差。

2.1 径向井方位角对裂缝扩展的影响

依据前置液造缝模型和酸液溶蚀模型，径向井辅助前置液酸压模拟结果如图5、6所示。模拟结果可分为前置液造缝部分应力场、酸液溶蚀部分孔隙度场与裂缝刚充满酸液时的压力场。

由图5可得，对于常规前置液酸压，前置液造缝部分主要形成沿最大主应力方向扩展的平直裂缝，不发生偏转现象，在后续酸液溶蚀过程中，酸液优先充满裂缝区域后溶蚀地层形成酸压裂缝。由图6可以看出，对于径向井辅助前置液酸压，由于径向井的存在改变了周围地层应力状态，打破了常规前置液酸压裂缝主要沿最大主应力方向扩展的限制，可使裂缝偏离最大主应力方向，从而实现开发非主应力方向油气藏、提高油气藏动用程度的目标。

径向井方位角为15°、30°、60°和75°时，对应的偏离系数分别为0.005、0.021、0.037和0.069。由此可见，偏离系数随着径向井方位角的增加而增加，当径向井方位角由15°增加至75°，偏离系数增大了13.8倍，引导效果大幅度减弱。这是由于当径向井方位角增加时，径向井改变应力场所产生的水平拉应力减小，导致裂缝更快被原地应力控制，从而偏向水平最大主应力方向扩展。由图6可见，当径向井方位角小于30°时，径向井引导效果明显，其中当径向井方位角为15°时，偏离系数为0.005，裂缝沿径向井扩展14.32 m后偏向最大主应力方向，引导效果最佳。当径向井方位角大于60°时，径向井引导效果显著减弱，裂缝沿径向井底部起裂后快速偏向最大主应力方向。可见，60°径向井已不能有效引导裂缝沿径向井方向扩展，为了更有效发挥径向井的引导作用，后续研究均采用30°方位角作为基本条件。

2.2 径向井长度对裂缝扩展的影响

径向井长度对径向井引导效果的影响如图7所示。径向井长度为10、15和20 m时，对应的偏离系数分别为0.029、0.021和0.0316。由图7可知，径向井长度决定着径向井对地层应力场的改变程度，当径向井长度增长时，径向井改变原地层应力场所产生的水平拉应力变大，使裂缝沿径向井方向的扩展距离更长，径向井的引导效果越好。

2.3 水平地应力差对裂缝扩展的影响

保持最大水平主应力为41 MPa不变，仅改变最小水平主应力。水平地应力差对径向井引导效果的影响如图8所示。水平地应力差为2、3、5和10 MPa时，对应的偏离系数分别为0.014、0.021、0.043和0.066。由图8可知，偏离系数随着水平地应力差的增加而增加，较大的水平地应力差会削弱径向井的引导作用。由于水平最小主应力的减弱，在径向井改变的地应力不变时，地层在水平最小主应力方向所需的破裂压力增大，裂缝的起裂及扩展方向更易偏向最大主应力方向。当水平应力差达到10 MPa时，裂缝几乎直接偏向最大水平主应力方向，未充分发挥出径向井的引导能力。对于该模型，水平应力差增加8 MPa，偏离系数增大4.36倍，径向井的引导能力大幅度减弱。

2.4 地层弹性模量对裂缝扩展的影响

弹性模量对径向井引导效果的影响如图9所示。弹性模量为12.9、22.9和32.9 GPa时，对应的偏离系数分别为0.021、0.025和0.029。由图9可知，偏离系数随着地层弹性模量的增加而增加，较大的地层弹性模量会减弱径向井的引导作用。地层弹性模量越大，地层的抗形变能力越强，当地层弹性模量增加时，裂缝宽度变小，较窄的裂缝减小了工作流体的有效面积，削弱了由径向井产生的水平拉应力，使径向井的引导能力减弱。

2.5 主控因素

灰色关联分析方法［10-13，27］是一种利用各因素间趋势相似性来度量因素间影响程度的数学方法，影响程度越大，灰色关联系数越大。本文中引入灰色关联分析方法重点分析了径向井方位角、径向井长度、水平地应力差和地层弹性模量4个因素对偏离系数的影响程度。

根据模拟试验所得数据，对影响偏离系数的因素进行无量纲均值化处理，并计算各因素与偏离系数间的关联系数，其中径向井方位角、径向井长度、水平地应力差、地层弹性模量与偏离系数间的关联系数分别为0.7434、0.6416、0.7637、0.6327。各因素的关联系数均大于0.6，表明上述因素与偏离系数均有较强相关性。此外，上述因素对偏离系数的影响程度由强到弱依次为水平地应力差、径向井方位角、径向井长度、地层弹性模量。因此当应用径向井辅助前置液酸压技术时，应首先优化径向井方位角并考虑原水平地应力差，再依据现场情况确定径向井长度等施工参数，以达到最佳的引导效果。

3 结 论

（1）当径向井方位角、水平地应力差和地层弹性模量越小，径向井长度越长时，偏离系数越小，径向井引导效果越好。当径向井方位角从15°增加至75°，偏离系数增加了13.8倍；当水平地应力差从2 MPa增加至10 MPa，偏离系数增加了4.36倍；当地层弹性模量从12.9 GPa增加至32.9 GPa，偏离系数增加了0.38倍；当径向井长度从10 m增加至20 m，偏离系数减少了66%。

（2）水平地应力差是对径向井引导效果的主控因素，当应用径向井辅助前置液酸压技术时，应首先优化径向井方位角，并根据现场情况综合考虑径向井长度等施工参数，以达到最佳的引导效果。

（3）当径向井方位角为15°时，裂缝沿径向井方向扩展14.32 m后偏向最大水平主应力方向，其偏离系数为0.005，说明径向井可以有效引导前置液酸压裂缝扩展，达到开发非主应力方向油气储集体、提高油气藏动用程度的目的。

参考文献：

［1］ 冯旭东.哈拉哈塘碳酸盐岩缝洞型油藏酸压效果评价研究［D］.成都：成都理工大学，2013.

FENG Xudong. Research on the acid fracturing effect evaluation in carbonate fracture-cavity reservoir of Halahatang［D］. Chengdu： Chengdu University of Technology， 2013.

［2］ 第五鹏祥，张潇，李彦阅，等.致密油藏水驱井间裂缝网络参数反演方法及应用［J］.中国海上油气，2022，34（4）：97-108.

DIWU Pengxiang， ZHANG Xiao， LI Yanyue， et al. Parametric inversion method and application of inter-well fracture network for water flooding tight oil reservoirs［J］. China Offshore Oil and Gas， 2022，34（4）：97-108.

［3］ 曲占庆，李小龙，李建雄，等.基于扩展有限元法的多径向井压裂裂缝形态［J］.中国石油大学学报（自然科学版），2018，42（1）：73-81.

QU Zhanqing， LI Xiaolong， LI Jianxiong， et al. Crack morphology of multiple radial well fracturing based on extended finite element method［J］. Journal of China University of Petroleum （Edition of Natural Science）， 2018，42（1）：73-81.

［4］ GUO T K， GONG F C， SHEN L， et al. Multi-fractured stimulation technique of hydraulic fracturing assisted by radial slim holes［J］.Journal of Petroleum Science and Engineering， 2019，174（2）：572-583.

［5］ NOVOKRESHCHENNYKH D V， RASPOPOV A V. Efficiency of radial drilling and acidizing technologies in carbonate reservoirs of Perm region（Russian）［J］.Neftyanoe Khozyaystvo-Oil Industry， 2016（4）：118-121.

［6］ 敬季昀，兰夕堂，邹剑，等.裂缝型储层复杂人工裂缝压后定量诊断方法研究［J］.中国海上油气，2023，35（5）：185-192.

JING Jiyun， LAN Xitang， ZOU Jian， et al. Research of quantitative diagnosis of complex hydraulic fractures for fractured reservoirs［J］. China Offshore Oil and Gas， 2023，35（5）：185-192.

［7］ 张方，高阳，李映艳，等.页岩油不同类型甜点对水平井压裂产能影响规律［J］.中国海上油气，2022，34（5）：123-131.

ZHANG Fang， GAO Yang， LI Yingyan， et al. Effects of different types of sweet spots on fracturing and productivity of horizontal wells in shale oil reservoirs［J］. China Offshore Oil and Gas， 2022，34（5）：123-131.

［8］ 鲜保安，夏柏如，张义，等.开发低煤阶煤层气的新型径向水平井技术［J］.煤田地质与勘探，2010，38（4）：25-29.

XIAN Baoan， XIA Bairu， ZHANG Yi， et al. Technical analysis on radial horizontal well for development of coalbed methane of low coal rank［J］. Coal Geology & Exploration， 2010，38（4）：25-29.

［9］ MEGORDEN M P， JIANG H， BENTLRY P J D. Improving hydraulic fracture geometry by directional drilling in a coal seam gas formation［R］. SPE 167053， 2013.

［10］ GUO T K， LIU B Y， QU Z Q， et al. Study on initiation mechanisms of hydraulic fracture guided by vertical multi-radial boreholes［J］. Rock Mechanics and Rock Engineering， 2017，50（7）：1767-1785.

［11］ CHEN Y， DING Y， LIANG C， et al. An analytical model for fracture initiation from a particular radial borehole in hydraulic fracturing guided bymultiradial boreholes［J］. Geofluids， 2021，2021：1-18.

［12］ GONG D G， QU Z Q， GUO T K， et al. Variation rules of fracture initiation pressure and fracture starting point of hydraulic fracture in radial well［J］. Journal of Petroleum Science and Engineering， 2016，140：41-56.

［13］ 龚迪光.径向井压裂裂缝起裂扩展规律与产能预测研究［D］.青岛：中国石油大学（华东），2016.

GONG Diguang. Study on the law of fracture initiation and propagation and productivity prediction for radial well-fracturing［D］. Qingdao： China University of Petroleum （East China）， 2016.

［14］ 薛衡，黄祖熹，赵立强，等.考虑岩矿非均质性的前置液酸压模拟研究［J］.天然气工业，2018，38（2）：59-66.

XUE Heng， HUANG Zuxi， ZHAO Liqiang， et al. A simulation study on the preflush acid fracturing considering rock heterogeneity ［J］. Natural Gas Industry， 2018，38（2）：59-66.

［15］ 薛衡，何冰，蒋利平，等.碳酸盐岩储层水平井靶向酸化研究及应用［J］.西南石油大学学报（自然科学版），2022，44（4）：121-128.

XUE Heng， HE Bing， JIANG Liping， et al. Researchand application of targeted acidizing tech in horizontal well of carbonate reservoir［J］. Journal of Southwest Petroleum University （Science & Technology Edition）， 2022，44（4）：121-128.

［16］ 党录瑞，周长林，黄媚，等.考虑多重滤失效应的前置液酸压有效缝长模拟［J］.天然气工业，2018，38（7）：65-72.

DANG Lurui， ZHOU Changlin， HUANG Mei， et al. Simulation of effective fracture length of prepad acid fracturing considering multiple leak-off effect［J］. Natural Gas Industry， 2018，38（7）：65-72.

［17］ 谢海.扩展有限元法的研究［D］.上海：上海交通大学，2009.

XIE Hai. Research of the extended finite element method［D］. Shanghai： Shanghai Jiao Tong University， 2009.

［18］ PANGA M K R， ZIAUDDIN M， BALAKOTAIAH V. Two-scale continuum model for simulation of wormholes in carbonate acidization［J］. AICHE Journal， 2005，1（12）：3231-3284.

［19］ 黄朝琴，姚军，王月英，等.基于离散裂缝模型的裂缝性油藏注水开发数值模拟［J］.计算物理，2011，28（1）：41-49.

HUANG Zhaoqin， YAO Jun， WANG Yueying， et al. Numerical simulation on water flooding development of fractured reservoirs in a discrete-fracture model［J］. Chinese Journal of Computational Physics， 2011，28（1）：41-49.

［20］ 姚军，黄朝琴，王子胜，等.缝洞型油藏的离散缝洞网络流动数学模型［J］.石油学报，2010，31（5）：815-819，824.

YAO Jun， HUANG Zhaoqin， WANG Zisheng， et al. Mathematical model of fluid flow in fractured vuggy reservoirs based on discrete fracture-vug network［J］. Acta Petrolei Sinica， 2010，31（5）：815-819，824.

［21］ 陈国彬.缝洞型碳酸盐岩油藏酸蚀蚓孔扩展机理研究［D］.青岛：中国石油大学（华东），2020.

CHEN Guobin. Study on the mechanism of wormhole propagation in fractured-vuggy carbonate reservoirs［D］. Qingdao： China University of Petroleum （East China）， 2020.

［22］ QI N， CHEN G， LIANG C， et al. Numerical simulation and analysis of the influence of fracture geometry on wormhole propagation in carbonate reservoirs ［J］. Chemical Engineering Science， 2019，198：124-143.

［23］ 熊健，吴俊，刘向君，等.陆相页岩储层地质力学特性及对压裂效果的影响［J］.西南石油大学学报（自然科学版），2023，45（5）：69-80.

XIONG Jian， WU Jun， LIU Xiangjun， et al. The geomechanical characteristics of the continental shale reservoirs and their influence on the fracturing effect［J］. Journal of Southwest Petroleum University （Science & Technology Edition）， 2023，45（5）：69-80.

［24］ GUPTA N， BALAKOTAIAHV. Heat and mass transfer coefficients in catalytic monoliths［J］. Chemical Engineering Science， 2001，56（16）：4771-4786.

［25］ GUO T K， QU Z Q， GONG F C， et al. Numerical simulation of hydraulic fracture propagation guided by single radial boreholes［J］. Energies， 2017，10（10）：1680.

［26］ LIU X， QU Z Q， GUO T K， et al. An innovative technology of directional propagation of hydraulic fracture guided by radial holes in fossil hydrogen energy development［J］. International Journal of Hydrogen Energy， 2019， 44（11）：5286-5302.

［27］ 连承波，李汉林，钟建华，等.基于灰色关联分析的储层含油气性气测解释方法［J］.中国石油大学学报（自然科学版），2008，32（1）：29-32.

LIAN Chengbo， LI Hanlin， ZHONG Jianhua， et al. Gas logging interpretation method of oil-gas potential reservoirs based on grey correlation analysis［J］. Journal of China University of Petroleum（Edition of Natural Science）， 2008，32（1）：29-32.

（编辑 李志芬）

基金项目：国家自然科学基金项目（51874336）

第一作者及通信作者：齐宁（1980-），男，教授，博士，博士生导师，研究方向为储层改造与提高采收率。E-mail：qining@upc.edu.cn。

引用格式：齐宁，甘俊冲，章泽辉，等.径向井辅助前置液酸压裂缝扩展数值模拟［J］.中国石油大学学报（自然科学版），2024，48（3）：101-110.

QI Ning， GAN Junchong， ZHANG Zehui， et al. Numerical simulation of fracture propagation guided by radial well assisted preflush acid fracturing［J］. Journal of China University of Petroleum（Edition of Natural Science），2024，48（3）：101-110.