基于模型预测控制的双轮平衡轮椅轨迹跟踪

常宏 王赜

摘要：为实现双轮平衡轮椅的自主循迹出行，根据欧拉-拉格朗日方程建立双轮平衡轮椅的动力学模型，通过差动几何模型建立运动关系，采用Pure Pursuit算法规划系统的目标运动状态，分别采用模型预测控制（model predictive control，MPC）及线性二次型最优控制（linear quadratic regulator，LQR）对双轮平衡轮椅进行平衡控制及运动状态追踪。通过软件Simulink搭建双轮平衡轮椅控制仿真系统，验证双轮平衡轮椅系统分别采用LQR和MPC控制器时的轨迹跟踪效果及跟踪平稳性。仿真结果表明：MPC控制器的动态响应速度较LQR控制器快，MPC控制器作用下车体能快速恢复稳定状态；轨迹跟踪时，MPC控制器在启动转向及终点位置对车体倾角及速度的稳定控制优于LQR控制器。

关键词：双轮平衡轮椅；LQR控制器；MPC控制器；轨迹追踪

中图分类号：U489;TP242.6文献标志码：A文章编号：1672-0032（2024）02-0001-09

引用格式：常宏，王赜.基于模型预测控制的双轮平衡轮椅轨迹跟踪［J］.山东交通学院学报，2024，32（2）：1-9.

CHANG Hong，WANG Ze. Trajectory tracking of two-wheel balanced wheelchair based on model predictive control［J］.Journal of Shandong Jiaotong University，2024，32（2）：1-9.

0 引言

轮椅是出行不便人员的辅助行动工具之一，一般通过人工协助、手柄遥控等方式完成轮椅的行动动作。随轮椅使用者的自主性出行需求和出行质量要求的提高，使轮椅适应更复杂的道路环境，提高轮椅的安全性及乘坐舒适性变得至关重要。

常宏等[1]采用双轮平衡轮椅系统结合圆弧齿架设计能自助上下楼的轮椅，但未进行完整路径追踪控制。双轮平衡轮椅系统有高度非线性特征，受力复杂，茅力非[2]采用拉格朗日运动方程建立座椅自平衡双轮机器人在平坦路面和颠簸路面的动力学模型；Yang等[3]引入边界函数，建立双机械臂非线性复杂内力系统的动力学模型。为实现平衡系统的控制与状态跟踪，刘学明等[4]基于后退方法，采用运动学跟踪控制器和动力学跟踪控制器，实现双轮平衡车在不确定运动下的参数自动调节；黄用华等[5]采用线性二次型最优控制（linear quadratic regulator，LQR）设计双轮自行车系统点对点运动的轨迹控制器。针对平衡系统模型与控制的结合及参数调优等问题，黄鹤等[6]采用拉格朗日方程构建双轮平衡机器人系统动力学方程，采用改进的食肉植物算法（improved carnivorous plant algorithm，ICPA）优化LQR权重系数，对双轮平衡机器人进行高精度轨迹跟踪；高志伟等[7]采用拉格朗日方程构建双轮自平衡小车系统的动力学方程，通过LQR优化比例积分微分（proportional integral derivative，PID）控制，提高小车的轨迹跟踪性能，降低能量消耗；Murcia等[8]、Yue等[9]基于PID控制器控制双轮倒立摆机器人的运动轨迹；宁一高[10]考虑避障运动问题，采用LQR控制器对双轮平衡车进行路径规划。模型预测控制（model predictive control，MPC）不仅适用于线性系统，在非线性系统中也有较好的适应性，已在自动驾驶领域得到广泛应用，梁栋[11]、龚大为[12]基于阿克曼车辆动力学模型，将MPC控制器应用于车辆控制及轨迹追踪；Yuan等[13]通过将LQR控制器与MPC控制器结合实现对车辆不确定状态的适应性控制。PID控制器通常不需对系统建模，通过调节PID参数即可实现期望动作，但易出现超调、控制量过大等问题；LQR控制器基于线性化后的动力学模型，在平衡点附近实现车体的控制响应，但仅结合当前的状态反馈进行控制，易使被控对象陷入当前最优状态；MPC控制器基于被控对象当前状态及未来时间的预测结果实施控制，控制效果较好。

双轮平衡轮椅为典型的非线性、欠驱动模型[14-16]，仅依靠运动几何关系，在期望状态附近线性化构建控制律难以实现对车体的平衡控制和规划轨迹的稳定跟踪。为改善车体平衡控制及轨迹追踪效果，本文采用MPC控制器改进双轮平衡轮椅的控制系统，使双轮平衡轮椅实现自主路径追踪，通过软件Simulink搭建双轮平衡轮椅控制仿真系统，验证系统的轨迹跟踪效果。

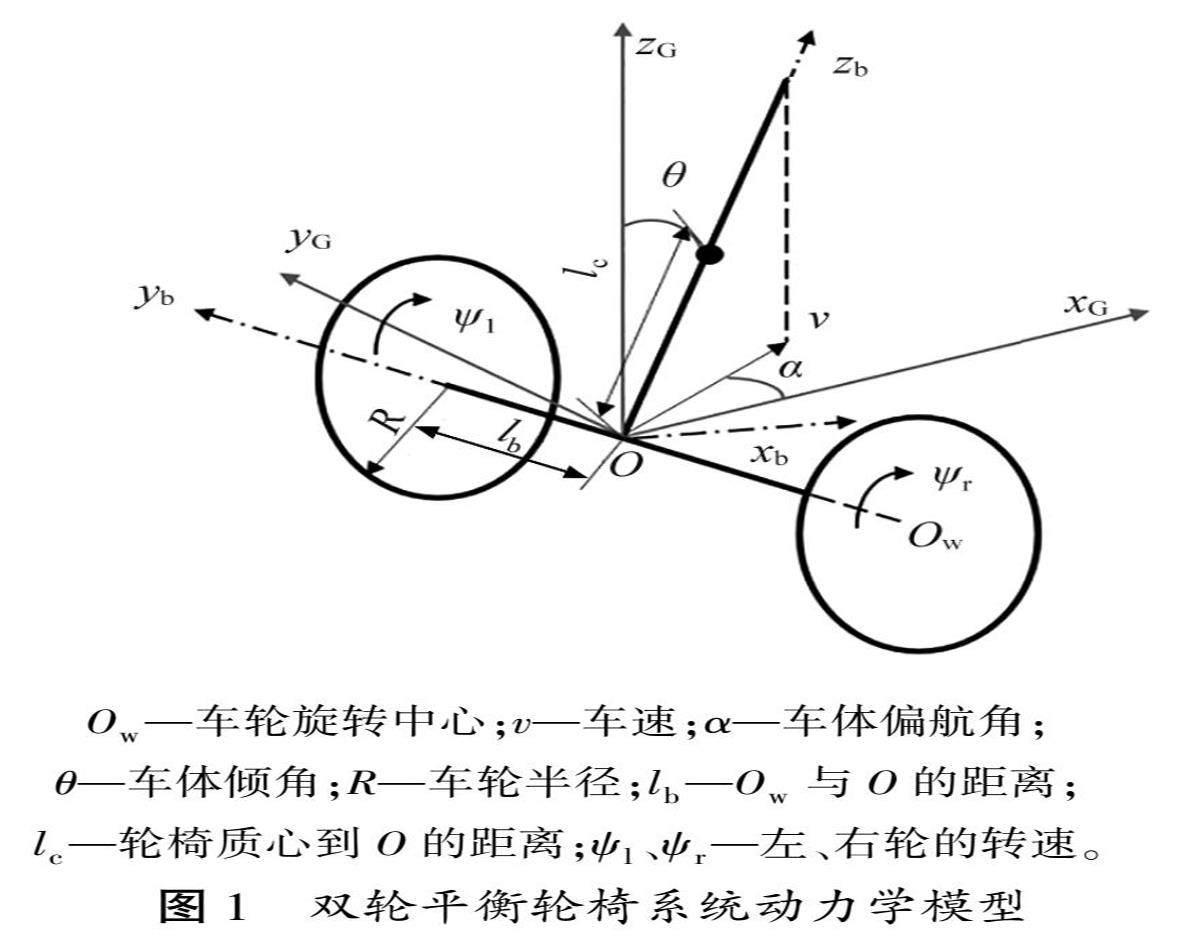
1 动力学建模

Ow—车轮旋转中心；v—车速；α—车体偏航角；

θ—车体倾角；R—车轮半径；lb—Ow与O的距离；

lc—轮椅质心到O的距离；ψl、ψr—左、右轮的转速。

为避免分析双轮平衡轮椅系统内部运动副约束，采用拉格朗日方程求解系统的动力学问题[2，17-18]。建立双轮平衡轮椅系统的动力学模型，如图1所示，以轮椅2个车轮旋转中心连线的中点为坐标原点O，车体处于平衡位置时，以垂直于车轴和车体组成的平面，水平向前为xG轴，以垂直于大地竖直向上为zG轴，以垂直于xG和zG组成的平面，由右轮指向左轮为yG轴，建立大地笛卡尔坐标系OxGyGzG，固定在轮椅起始位置，不随车体移动；以垂直车轴和车体所构成的平面，指向车体前进方向为xb轴，以垂直于xb轴，由右轮指向左轮方向为yb轴，以垂直于xb轴和yb轴构成的平面，向上方向为zb轴，建立车体笛卡尔坐标系Oxbybzb，其随车体移动而移动。双轮平衡轮椅的结构参数如表1所示。

注：mw、mb分别为车轮、车体的质量，Iwa为车轮转动惯量，Iwd为车轮绕直径方向的转动惯量，Ixx、Iyy、Izz分别为车体对xb、yb、zb轴的转动惯量，fb为车身运动粘滞阻力的耗散能系数，fw为地面粘滞阻力的耗散能系数。

双轮平衡轮椅车体转动动能

TRb=IbGω2/2，

式中：IbG为车体相对大地笛卡尔坐标系的惯性矩，ω为车体转动角速度。

双轮平衡轮椅车体平动动能

TTb=mbvbG2/2，

式中vbG为车体平动速度。

选取双轮平衡轮椅车轴所在平面为零势能面，车体势能

Vb=mbglccos θ，

式中g为重力加速度。

双轮平衡轮椅车轮转动动能

TRw=Iwaψr·2+Iwaψl·2+2Iwdθ·2/2，

式中：ψl·、ψr·分别为左、右轮的转动角速度，θ·为车体倾斜角速度。

双轮平衡轮椅车轮平动动能

TTw=mwR2（ψr·2+ψl·2）/2。

阻力会造成能量损失，双轮平衡轮椅系统运转的能量损失

D=fw（ψr·2+ψl·2）+fbθ·2/2。

拉格朗日方程从能量角度求解动力学模型，计算双轮平衡轮椅系统的机械能

L=TRb+TTb+TRw+TTw－Vb。

选取初始状态变量q=x y θ α ψrψlT，建立双轮平衡轮椅系统的拉格朗日方程为：

ddt-L-q·－-L-q+-D-q·=Eqτ+AT（q）λ，

式中：τ为车轮转矩输入矩阵，τ=τrτlT，其中τl、τr分别为左、右转轴的转矩；A（q）为系统的非完整约束矩阵；λ为拉格朗日乘子；Eq为简化后转矩矩阵的系数矩阵，表达式为：

E（q）=000000－110－101T。

考虑车轮处于纯滚动状态，满足A（q）q·=0，则：

A（q）=－sin αcos αcos αsin αcos αsin α00b0－b000－R00－R。

A（q）的零空间矩阵S（q）使A（q）S（q）=0，则：

S（q）=00cos αsin α00010010001/R1/Rb/R－b/RT。

q·与Sq间满足

q·=Sqυ，

式中：υ为车体运动状态向量，υ=θ· v α·T，其中α·为车体偏航角速度。

根据欧拉-拉格朗日法建立双轮平衡轮椅的动力学方程为：

Mqq··+Vq，q·=Eqτ+AT（q）λ，（1）

式中：Mq为状态变量二阶项系数矩阵，Vq，q·为状态变量及状态变量一阶项描述矩阵，q··为状态变量的二阶导数。

式（1）两边同乘ST（q）得：

［ST（q）M（q）S（q）］υ·+ST（q）［M（q）S·（q）υ+V（q，q·）］=ST（q）E（q）τ，

式中S·（q）为S（q）对q的一阶导数。

ψr、ψl可通过θ·、v表达，初始状态变量修正为q=（xyθα）T，为实现系统的平衡及速度控制，选取状态变量为x=（θαθ·vα·）T，控制量u=（τrτl）T，建立系统状态方程为：

x·=g（x）u+f（x），（2）

式中：g（x）为系统输入矩阵，g（x）=02×2ST（q）M（q）S（q）－1ST（q）E（q）；f（x）系统状态矩阵，f（x）=θ·α·－ST（q）M（q）S（q）－1ST（q）［M（q）S·（q）υ+V（q，q·）］。

2 模型预测控制

MPC依据系统模型状态预测未来时间状态，通过优化系统状态与目标状态的误差求解控制量。轨迹跟踪中已知目标路径，MPC可结合更多的状态因素优化控制量。

由式（2）可知：双轮平衡轮椅动力学系统为非线性系统，正常工作时状态基本稳定在平衡点，即θ=0，θ·=0，对该系统在平衡点处进行麦克劳林展开，忽略高次项，得状态偏差的一阶导数

x·=Ax+Bu，

式中：x为状态偏差，x=x－xd，其中xd为期望目标状态；u为输入偏差，u=u－ud，其中ud为预期输入状态；A、B为线性系数矩阵，A=00100

00001

a310a33a340

a410a43a440

a510000a55，

B=00b31b41b5100b32b42b52，A、B中各元素的表达式分别为：

a31=［2（2mwIxx+mbIxx－mbIzz－2mwIzz）R2α·2－4mwmbR2glc+4Iwambl2cα·2－4Iwamblcg+4mwmbR2l2cα·2+

4（Ixx－Izz）Iwaα·2－2m2bR2glc］/K1，K1=－4IyymwR2－4mbmwl2cR2－4IyyIwa－4mbl2cIwa－2IyymbR2，a41=

［（Iyy－Ixx+Izz）mbR2lcα·2+m2bR2l2cg+m2bR2l3cα·2］/K2，K2=－IyymbR2－2IyyIwa－2IyymwR2－2mbl2cIwa－

2mbmwl2cR2，a51=mblcR2vα·/K3，K3=IzzR2+2IwdR2+2Iwdb2+2mwb2R2，a33=［－4Iwafb－（4mw+

2mb）R2 fb］/K1，a34=mbR2lcfb/K2，a43=4mblcfw/K1，a44=（－2fwmbl2c－2fwIyy）/K2，a55=2fwb2/K3，b31=b32=（mbR2+2Iwa+2mwR2+mblcR）/K1，b41=b42=－R（mblcR+Iyy+mbl2c）/K2，b51=－b52=bR/K3。

通过前向欧拉法将连续系统转换为离散系统，采样周期为T，k+1时刻的状态误差

xk+1=A—xk+B—uk，

式中：xk为k时刻的状态误差；uk为k时刻的输入变化量；A—、B—为系统离散化后线性系数矩阵，A—=I+AT，I为单位矩阵，B—=BT。

取预测区间长度为N，x（k+i|k）、u（k+i|k）为系统在k时刻对k+i（i=1，2，…，N）时刻的预测状态，系统的预测误差为e=x－xr，预期目标xr=0，则e=x。为保证系统在预测区间内运行的状态误差、终末误差及控制量之和最小，构造系统的代价函数

J（x，u）=∑N－1i=0［x（k+i|k）TQx（k+i|k）+u（k+1|k）TRu（k+1|k）］+x（k+N|k）TFx（k+N|k），（3）

式中：Q为衡量系统状态误差的增益矩阵，R为系统输入变化量的增益矩阵，F为终态增益矩阵。

通过建立的离散系统方程可解得预测区间内系统状态预测为：

x（k|k）=xkx（k+1|k）=A—xk+B—u（k|k）x（k+2|k）=A—2xk+A—B—u（k|k）+B—u（k+1|k） x（k+N|k）=A—Nxk+A—N－1B—u（k|k）+…+B—u（k+N－1|k）。（4）

由式（4）得系统在k时刻的预测区间状态方程为：

Xk=Mxk+CUk，（5）

式中：Xk为预测N步的状态误差矩阵，M为k时刻状态误差的系数矩阵，Uk为预测N步的输入变化量，C为预测N步输入变化量的系数矩阵，表达式分别为：

Xk=x（kk）x（k+1|k）x（k+N|k），M=I5×5A—A—2A—N，Uk=u（kk）u（k+1|k）u（k+N－1|k），C=05×205×2…05×2

B—05×2…05×2

A—B—B—…05×2

A—N－1B—

A—N－2B—

…B—。

将式（5）代入式（3）得：

J（x，u）=XkTQ—Xk+UkTR—Uk=Mxk+CUkTQ—Mxk+CUk+UkTR—Uk=

xkTMTQ—Mxk+2xkTMTQ—CUk+UkT（CTQ—C+R—）Uk，（6）

式中：Q—为由状态增益矩阵与终态增益矩阵组成的对角阵，Q—=Q0…0

0Q…0

00…F；R—为输入变化量增益矩阵组成的对角阵，R—=R…00…R。

式（6）中xkTMTQ—Mxk为初始状态，不影响代价函数，可忽略，即将问题转化为求解令J（x，u）最小的预测N步的输入变化量Uk，可通过二次规划求解，最终可得系统在k时刻的控制量为Uk（1）。

图2 双轮平衡轮椅差动几何运动模型

构建双轮平衡轮椅差动几何运动模型如图2所示。用车体差动几何模型中心速度描述车体的行进速度

v=vl+vr/2，

式中vl、vr分别为左、右车轮的速度。

车体的偏航角速度α·可看作右轮相对左轮旋转的角速度，即

α·=vr－vl/l，

式中l为轮距。

采用Pure Pursuit算法[19]规划双轮平衡轮椅的目标轨迹，估计车体当前位置与目标点的距离偏差、角度偏差，得到车体转动角速度，即规划系统的α、α·及v，将运动规划结果作为动力学模型的期望结果，使双轮平衡轮椅系统依据自身的约束特性跟踪运动状态，实现双轮平衡轮椅对预期位置的轨迹跟踪，并保证响应速度与跟踪平稳性。

3 仿真与分析

3.1 仿真系统搭建

采用软件Simulink搭建双轮平衡轮椅控制仿真系统，包括双轮平衡轮椅动力学模型、LQR和MPC控制器、运动规划模块及显示模块，如图3所示。将既定行进轨迹输入运动规划模块得到双轮平衡轮椅的期望状态，通过LQR和MPC控制器进行期望状态跟踪。分析双轮平衡轮椅系统分别采用LQR、MPC控制器时的轨迹跟踪效果及跟踪平稳性。

图3 双轮平衡轮椅控制仿真系统

为使双轮平衡轮椅系统在控制器作用下稳定运行，设定LQR控制器的系统状态增益矩阵QLQR及系统输入增益矩阵RLQR分别为：

QLQR=1 000 0 0 0  0

0100 0 0  0

0 0100 0  0

0 0 0100  0

0 0 0 01 000，RLQR=0.01 00  0.01。

设定MPC控制器的系统状态增益矩阵QMPC及系统输入增益矩阵RMPC分别为：

QMPC=100000

050000

001000

0001000

00001 000，RMPC=0.05 00  0.05。

通过MATLAB中的lqr函数求解LQR控制器的反馈增益K，得到LQR控制律为u=－Kx。

借助MATLAB二次规划函数quadprog求解式（6），可得预测区间内的Uk，则当前时刻MPC控制律为u=Uk（1）。

3.2 系统动态响应

设定双轮平衡轮椅系统初始状态x=0.090010T，即初始时刻θ=009 rad，v=1 m/s，车体期望状态为平衡位置即自平衡状态（θ=0，v=0），验证双轮平衡轮椅系统分别在LQR和MPC控制器作用下的稳定性，仿真结果如图4所示。

a）LQR控制器                        b）MPC控制器

图4 LQR和MPC控制器对双轮平衡轮椅系统的稳定性控制

由图4可知：LQR和MPC控制器均可使车体从初始状态恢复至平衡稳定状态，MPC控制器作用下车体可较快达到稳定状态。

设定双轮平衡轮椅系统初始状态为平衡位置，车体目标状态为xd=00010T，即以v=1 m/s稳定前进，验证LQR和MPC控制器对双轮平衡轮椅系统速度的控制情况，仿真结果如图5所示。由图5可知：LQR和MPC控制器均可实现对双轮平衡轮椅系统速度的跟踪控制，在MPC控制器作用下车体较快响应至目标速度附近。

a）LQR控制器b）MPC控制器

图5 LQR和MPC控制器对双轮平衡轮椅系统的速度控制

双轮平衡轮椅系统的动态响应指标如表2所示。由表2可知：MPC控制器的动态响应速度较LQR控制器快，二者在速度跟踪中均因系统线性化引入的模型偏差而无法准确追踪速度，但MPC控制器的速度跟踪稳态误差较LQR控制器小。

3.3 系统轨迹追踪

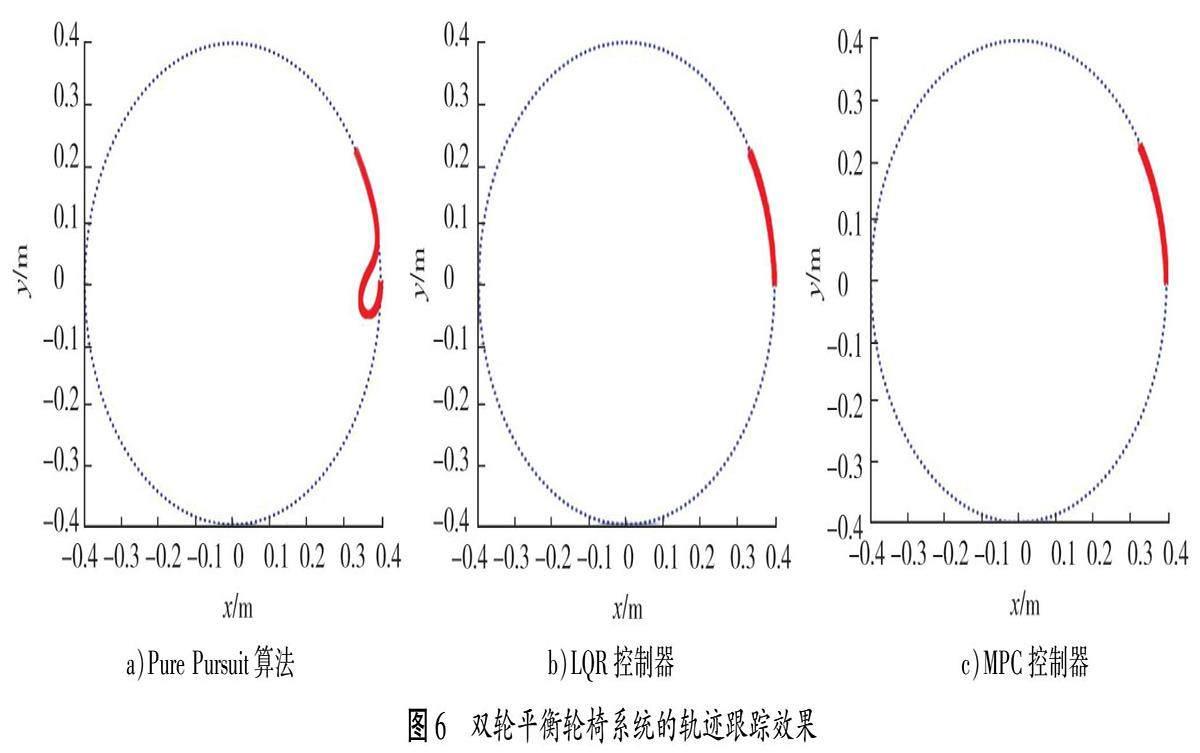
设定目标轨迹为半径0.4 m的圆形，循迹速度为0.2 m/s，双轮平衡轮椅系统初始状态为x=（0－1.5000）T，初始位置坐标为（0.4 m，0），轮椅初始正方向与x轴夹角为－90°。分别采用Pure Pursuit算法、LQR控制器和MPC控制器跟踪目标轨迹，仿真结果如图6所示。由图6可知：Pure Pursuit算法仅通过运动几何关系跟踪目标轨迹，初始阶段需较大的转弯半径，LQR和MPC控制器的转弯半径明显减小。

a）Pure Pursuit算法             b）LQR控制器              c）MPC控制器

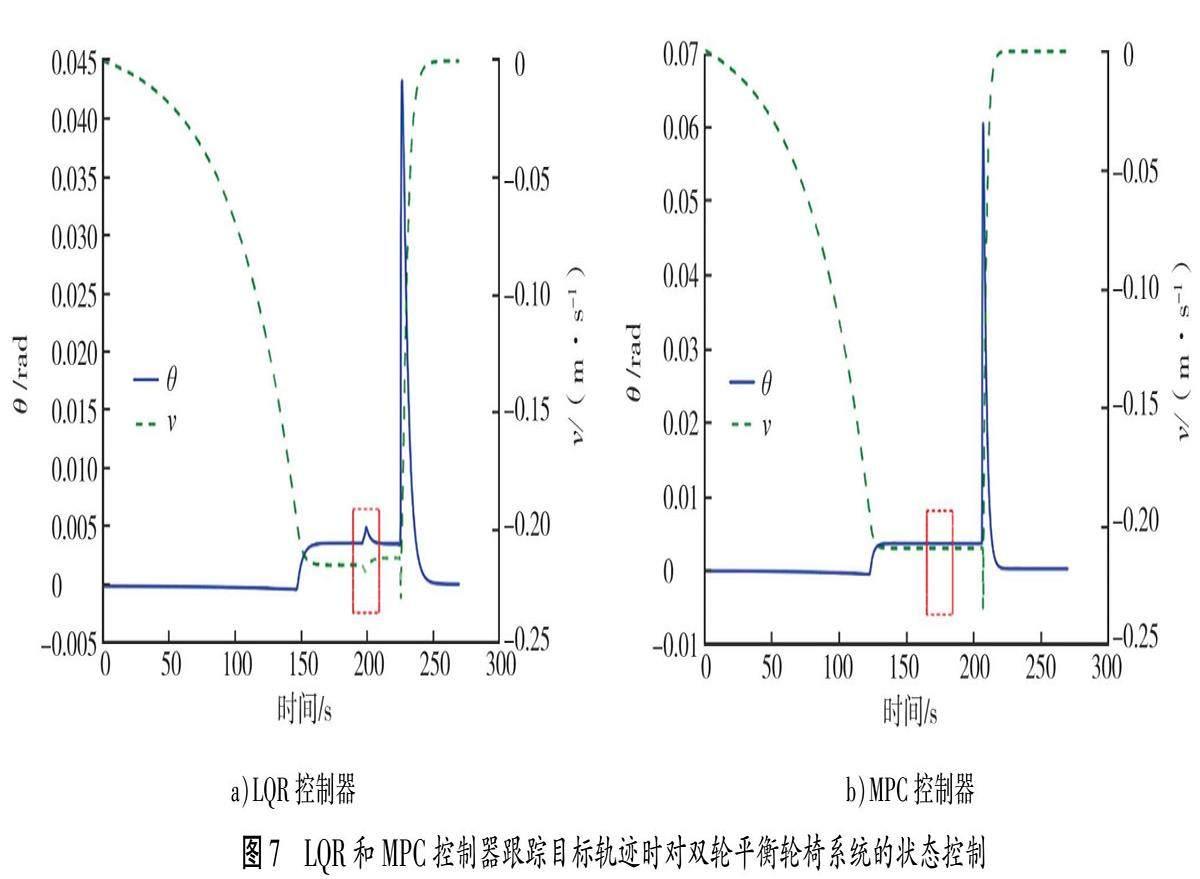
LQR和MPC控制器跟踪目标轨迹时对双轮平衡轮椅系统的状态控制如图7所示。由图7可知：LQR和MPC控制器均对双轮平衡轮椅系统状态有较好的控制，车体速度逐步达到并稳定在目标速度附近，倾角始终稳定在0°附近，由于要保持一定行进速度，车体略向前倾，即θ>0°；当轮椅抵达终点位置时，速度急剧减小，由于惯性车体短时间内前倾角较大，但二者均可较好的控制车体平衡，恢复至平衡状态。MPC控制器可较快完成规划路径的循迹，用时225 s，LQR控制器用时250 s，前者提前25 s达到指定速度，响应速度较快；LQR控制器在经过200 s（轮椅行进至270°附近）时车体倾角状态出现抖动（图7虚线框选位置），MPC控制器在整个循迹周期内倾角和速度状态较平稳，控制效果较好。

a）LQR控制器                        b）MPC控制器

在终点位置，双轮平衡轮椅系统因自身惯性无法形成Pure Pursuit算法的瞬间停止机制，LQR与MPC控制器的动力学控制更接近实际运行情况。LQR与MPC控制器对双轮平衡轮椅系统的终点控制如图8所示。

a）LQR控制器                      b）MPC控制器

图8 LQR与MPC控制器对双轮平衡轮椅系统的终点控制

由图8可知：当轮椅到达终点位置（0.4 m，0）时，车速没有瞬间为0而是保持当前的运动状态，在控制器的作用下逐步修正车体状态后停止。从终点处的实际追踪轨迹来看，轮椅在LQR控制器作用下，越过终点位置后，未能及时到达目标状态，徘徊于目标位置附近；MPC控制器相较于LQR控制器可较快到达目标状态，原因是MPC控制器在控制过程中引入未来一段时间的信息，获得与目标路径更适配的控制量。

LQR和MPC控制器完成目标路径跟踪的平均误差分别为0.047、0.046 m，跟踪精度相似。MPC控制器引入未来时间的状态信息进行跟踪优化，在跟踪稳定性及终点位置的控制表现较好。

4 结束语

通过欧拉-拉格朗日方程建立双轮平衡轮椅系统非线性动力学模型，对其进行线性化及离散化，建立预测区间内状态误差、输入误差及终点误差的代价函数，采用二次规划求解当前时刻的最优控制输入。通过与几何模型追踪控制和LQR控制器追踪控制对比，MPC控制器对双轮平衡轮椅系统控制有较快的动态响应，在轨迹跟踪过程引入系统内部约束及未来状态信息，在追踪启动、终点处有效控制系统，优化跟踪路径。本文仅针对平坦水平路面进行动力学建模分析，可继续研究在斜面及颠簸路面的轨迹跟踪。

参考文献：

[1] 常宏，常鹏，蒋维，等.基于平衡车的自助上下楼梯轮椅[J].山东交通学院学报，2017，25（4）：71-75.

[2] 茅力非.两轮自平衡移动机器人建模与控制研究[D].武汉：华中科技大学，2013.

[3] YANG C， JIANG Y， LI Z， et al. Neuralcontrol of bimanual robots with guaranteed global stability and motion precision[J].IEEE Transactions on Industrial Informatics， 2017，13（3）：1162-1171.

[4] 刘学明，梁春兰，王学东.两轮驱动非完整约束机器人轨迹跟踪研究[J].制造业自动化，2013，35（16）：84-87.

[5] 黄用华，郭骞，庄未，等.两轮车自行车机器人的点对点位置控制[J].机械设计与研究，2022，38（2）：38-43.

[6] 黄鹤，李文龙，杨澜，等.ICPA-LQR优化的两轮平衡机器人自稳定与轨迹跟踪PID控制器设计[J/OL].哈尔滨工业大学学报.（2022-11-09）[2023-02-15].http：//kns.cnki.net/kcms/detail/23.1235.T.20221108.1333.002.html.

[7] 高志伟，代学武.自平衡小车LQR-PID平衡与路径跟踪控制器设计[J].控制工程.2020，27（4）：708-714.

[8] MURCIA H F， GONZALEZ A E. Performance comparison between PID and LQR control on a 2-wheel inverted pendulum robot[C]//2016 IEEE Colombian Conference on Robotics and Automation （CCRA）. Bogota， Colombia：IEEE，2016：1-6.

[9] YUE M， NING Y G， ZHAO X D， et al. Point stabilization control method for WIP vehicles based on motion planning[J].IEEE Transactions on Industrial Informatics， 2019，15（6）：3368-3378.

[10] 宁一高.考虑内稳定与外避障的两轮自平衡车轨迹规划与跟踪控制[D].大连：大连理工大学，2021.

[11] 梁栋.基于模型预测控制的无人驾驶汽车横纵向综合控制[D].重庆：重庆理工大学，2022.

[12] 龚大为.基于模型预测控制的自动驾驶汽车横向控制策略研究[D].重庆：重庆交通大学，2021.

[13] YUAN T F， ZHAO R C.LQR-MPC-based trajectory-tracking controller of autonomous vehicle subject to coupling effects and driving state uncertainties[J].Sensors，2022，22（15）：5556.

[14] 陈素霞，黄全振，高继勋.非完整约束移动机器人自适应轨迹跟踪控制设计[J].中国测试，2021，47（11）：80-84.

[15] 张震.非完整约束移动机器人的运动规划与跟踪控制技术研究[D].哈尔滨：哈尔滨工业大学，2021.

[16] 徐慧，孙宏图.全自主双轮平衡车数学建模与控制系统研究[J].机械设计，2022，39（7）：111-116.

[17] PATHAK K， FRANCH J， AGRAWAL S K. Velocity control of a wheeled inverted pendulum by partial feedback linearization[C]//2004 43rd IEEE Conference on Decision and Control. Nassau， Bahamas：IEEE， 2004：3962-3967.

[18] KUMAR E V， JEROME J. Robust LQR controller design for stabilizing and trajectory tracking of inverted pendulum[J].Procedia Engineering， 2013， 64：169-178.

[19] 刘延彬，姜媛媛.基于路标点追踪的差速驱动机器人运动规划[J].控制与决策，2023，38（9）：2529-2536.

Trajectory tracking of two-wheel balanced wheelchair based on

model predictive control

CHANG Hong，WANG Ze

School of Mechanical Engineering， Inner Mongolia University of Technology， Hohhot 010051， China

Abstract：In order to achieve the autonomous tracking travel of the two-wheel balanced wheelchair， a dynamic model of the two-wheel balanced wheelchair is established based on the Euler-Lagrange equation， and the motion relationship is established through the differential geometric model. The Pure Pursuit algorithm is used to plan the target motion state of the system， and model predictive control（MPC） and linear quadratic optimal control（LQR）are used to balance and track the motion state of the two-wheel balanced wheelchair. The simulation system for the control of the two-wheel balanced wheelchair is built through software Simulink to verify the trajectory tracking effect and tracking stability of the two-wheel balanced wheelchair system when LQR and MPC controllers are used. The simulation results show that the dynamic response speed of the MPC controller is faster than that of the LQR controller， and the MPC controller can quickly restore the stable state of the vehicle body when acting on the vehicle body; when tracking the trajectory， the MPC controller has better stable control of the vehicle body inclination angle and speed at the starting and ending positions than the LQR controller.

Keywords： two-wheel balanced wheelchair; LQR controller; MPC controller; trajectory tracking

（责任编辑：赵玉真）

收稿日期：2023-04-28

基金项目：内蒙古自治区关键技术攻关计划项目（2021GG0258）

第一作者简介：常宏（1992—），男，呼和浩特人，工学硕士，主要研究方向为机器人控制，E-mail：changhong@imut.edu.cn。

*通信作者简介：王赜（1974—），男，呼和浩特人，主要研究方向为飞行器制造，E-mail：wangze@imut.edu.cn。

DOI：10.3969/j.issn.1672-0032.2024.02.001