基于核心素养的高中概率统计的教学感悟
李菲菲

课题信息:南京市第十二期个人课题“基于核心素养的高中概率统计的教学研究”,课题编号为Ec317.
在“概率与统计”实际教学中,教师应重视学生数据分析、数学处理、数据建模等能力的培养,让学生经历数据处理的过程,掌握数据分析的方法.笔者结合“概率与统计”中的几个典型案例,谈谈对“概率与统计”教学的感悟.
1 明晰概率模型
概率主要是研究随机现象规律的学科,其在生活中随处可见,有着重要的应用价值,它是统计的思想基础,也是重要的工具.概率的模型众多,如高中阶段的概率初步模型中有几何概型、古典概型、互斥事件概率、条件概率等,随机变量模型中包括几何分布、正态分布、二项分布等.因其模型众多,为此理解并掌握这些概率模型成为了概率与统计的重点、难点和关键点.纵观历届高考容易发现,造成失分的主要原因就是很多学生对这些概率模型理解不深,在解题时常常张冠李戴.为此,在教学中教师要充分利用好教材资源,挖掘各种概率模型之间的区别和联系,揭示概率模型的本质特征,进而便于学生在解题时可以准确选择模型,顺利求解.
例1 现将号码各不相同的100张卡片放在抽奖箱中,从中任意抽取1张记录后,将其重新放回抽奖箱,重复20次.证明:p<91019<1e2(其中p表示抽得的20个号码互不相同的概率).
证法1:由已知可知这100张号码各不相同,这样若从中任意抽取1张则有100种结果,另外因为抽取并记录后又将其放回,为此连续抽取20次就有10020种结果,其中20个号码互不相同的有A20100种结果,每个结果都是等可能的,因此由古典概型的计算公式可得p=A2010010020,于是证明A2010010020<91019<1e2(不等式证明略).
证法2:因为抽取的20张卡片各不相同,为此在计算时可以分步进行.第1次抽取是在100张各不相同的卡片中抽取,则任抽1张的概率为100100;第2次同样有100张卡片,但因为第1次已经抽取了一张,则第2次抽出互不相同卡片的概率为99100;依次类推,第20次抽取时,卡片的总数依旧为100张,然前面已抽取了19次,则抽出互不相同卡片的概率为81100.由条件概率的计算公式得p=100100×99100×98100×……×81100,不等式证明略.
从学生解题的反馈来看,大多数学生从已知条件出发,根据题设信息判断其符合有限性、等可能性两大特点,所以选择应用古典概型来解决问题.不过在具体实施过程中,部分学生对结果是否有序理解不清,给出的答案为p=C2010010020,显然整体事件中包括了同一种号码排列顺序不同的情况,所以其正解不是p=C2010010020,而是p=A2010010020;也有的学生认为每次抽出后又放回,这样每次抽出已知号码概率均为1100,所以选择利用二项分布解决问题,但是从二项分布事件发生的次数为0,1,2……显然不适合二项分布.
为了让学生能够准确识别并应用各种概率模型,在完成例1的讲解后,笔者给出了如下变式题目进行强化练习.
变式1 现有10张编号由1到10的卡片,从中任取3张,求恰好有2张号码能被3整除的概率.
变式2 现有10张编号由1到10的卡片,从中任意抽取1张,记录号码后放回,重复3次,则随机抽取的3张卡片中,有2张恰好被3整除的概率是多少?
可见,概率问题是非常灵活多变的,稍加修改其解题思路就会完全不同,另外即使同一问题也可能蕴含着不同的概率模型.
为此,若想顺利求解,必须要掌握各个模型的本质特征,从而准确地识模用模.
2 熟识统计图表
图表可以直观呈现数据,为此在统计分析时自然离不开图表.识图用图也是高中数学教学的一项重要内容,对于识图,要具备能够从不同图表中提取重要信息的能力;对于用图,学生要明晰图表的功能,以便结合实际问题选择合适的图表,将使杂乱无章的数据转化为可视化的图表,进而使问题变得更加直观明了.
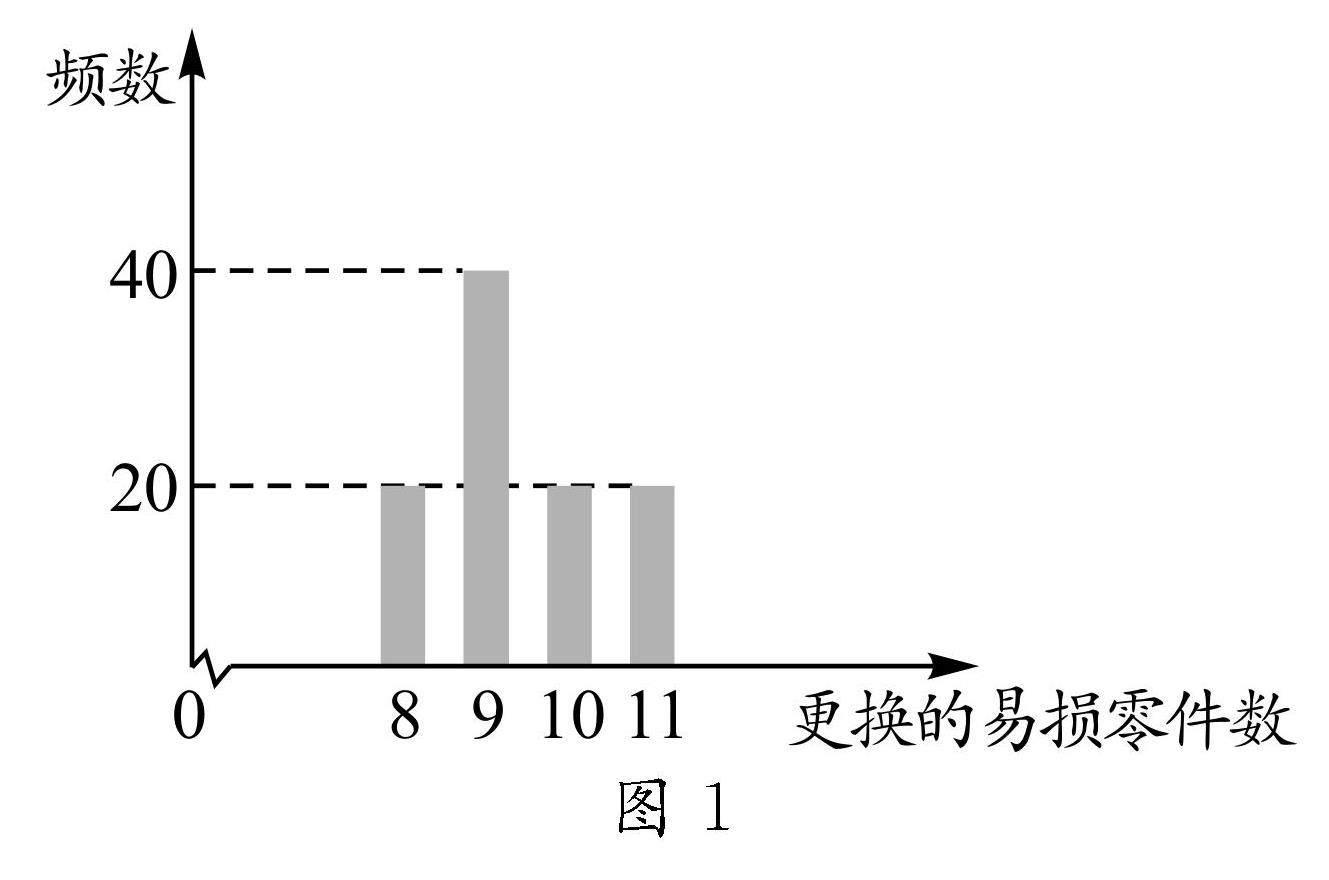
例2 某加工厂计划购买2台新机器,该机器的使用寿命为3年.机器上有一个零件极易破损,为此在购买新机器时可以同时购买一些易破损零件备用.若在购买新机器时同时购买,该零件每个只需200元,否则每个500元.为了寻求最佳的购买方案,该厂搜集并整理了100台同样型号机器3年内更换零件个数(如图1).
以100台机器更换该零件的频率代替1台机器更换该零件的概率,记X表示2台机器3年内共更换该零件的个数,n表示购买2台机器时购买该零件的个数.
(1)求X的分布列;
(2)若要求P(X≤n)≥0.5,确定n的最小值.
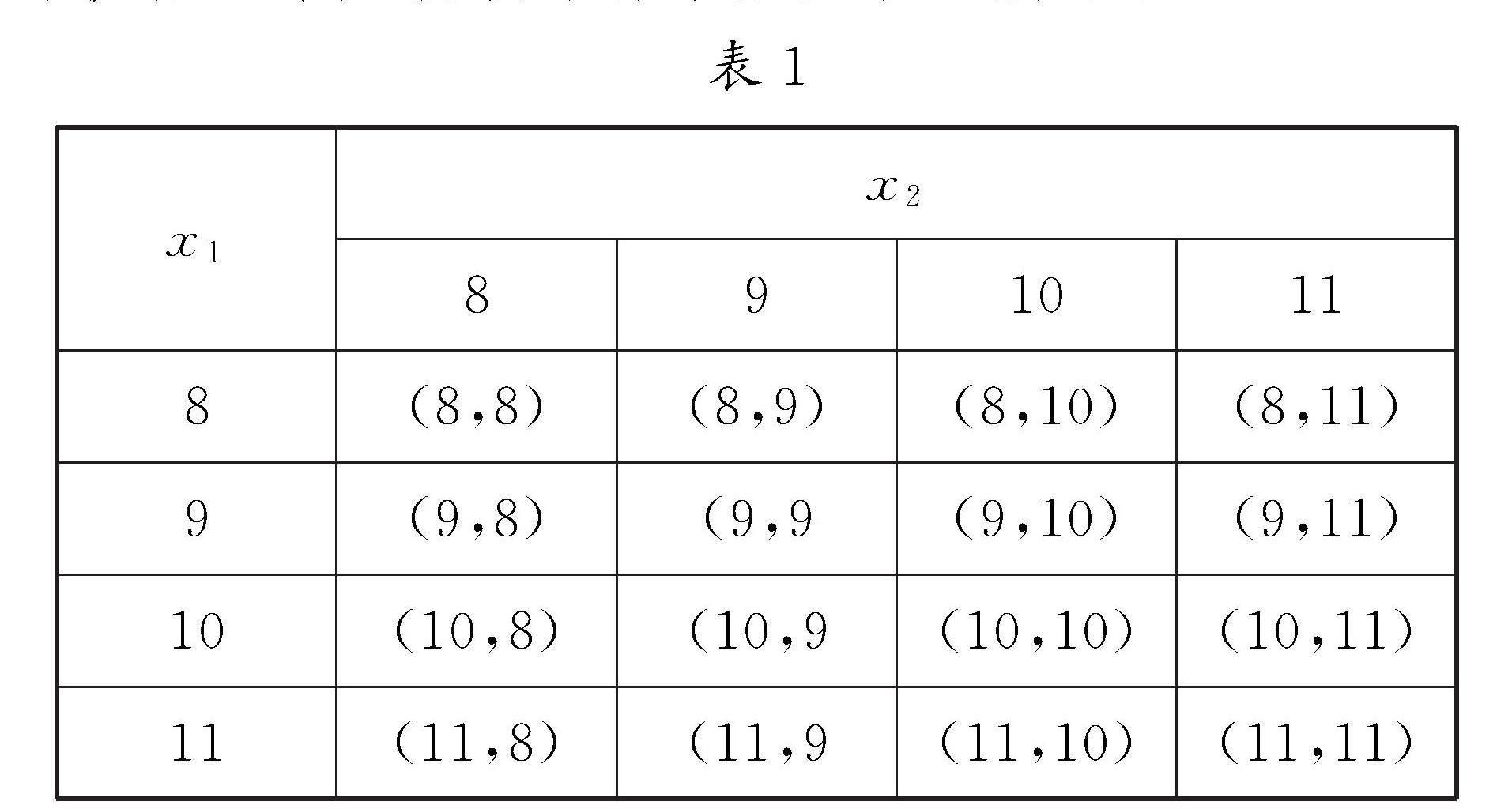
解析:由图1可知,1台机器在3年内更换的易损零件数分别为8,9,10,11的概率分别为0.2,0.4,0.2,0.2.令x1表示第一台机器3年内更换易损零件个数,x2表示第二台机器3年内更换易损零件个数,则两台计机器3年更换该零件个数如表1所示:
表1
x1
x2
891011
8(8,8)(8,9)(8,10)(8,11)
9(9,8)(9,9(9,10)(9,11)
10(10,8)(10,9(10,10)(10,11)
11(11,8)(11,9(11,10)(11,11)
这样结合表1,可得7种不同的结果.根据频数易得P(X=16)=P(x1=8)P(x2=8)=0.2×0.2=0.04;P(X=17)=P(x1=9)P(x2=8)+P(x1=8)\5P(x2=9)=2×0.2×0.4=0.16.同理可得
P(X=18)=2×0.2×0.2+0.4×0.4=0.24;
P(X=19)=2×0.2×0.2+2×0.4×0.2=0.24;
P(X=20)=2×0.2×0.4+0.2×0.2=0.2;
P(X=21)=2×0.2×0.2=0.08;
P(X=22)=0.2×0.2=0.04.
于是,可得X分布列如表2所示:
表2
X16171817202122
P0.040.160.240.240.20.080.04
(2)由表2可知,P(X≤18)=0.44,P(X≤19)=0.68,故满足P(X≤n)≥0.5的n的最小值为19.
由此可见,例2的两个问题主要考查了学生识图和用图的能力,利用图表逐渐将问题向简单化和直观化转化,大大提升了解题效率.
3 分解复杂事件
解决复杂事件时,一般先将事件字母化,即用字母A,B,C,Ai,Bj,Ck等表示所涉事件;然后将事件简单化,即将所求事件转化成彼此互斥的事件的和或先求对立事件的概念,再运用公式求解.这样将问题逐渐简单化,体现了转化思想在数学中的重要应用.
例3 质检部针对某批出口产品制订如下检测方案:优质品的件数记作n.
先从这批产品中任取4件进行检验,这4件中符合以下两种情况可以通过检测.第一种情况:若n=4,再从这批产品中任意一件,若为优质品,则通过检测;第二种情况:若n=3,再从这批产品中任抽4件进行检测,若都为优质品,则通过检测.假设这批产品的优质率为50%,求这批产品通过检测的概率.
解析:首先将事件字母化.
A1=“第一次任取4件产品中,n=3”;
B1=“第一次任取4件产品中,n=4”;
B2=“第二次任取的4件产品都为优质品”;
C2=“第二次任取1件为优质品”;
D=“通过检测”.
易得D=(A1B2)∪(B1C2),A1B2与B1C2互斥,A1与B2,B1与C2相互独立,任取4件产品中的优质品件数服从二项分布.分析至此,问题可以迎刃而解.
在解题时不要急于求成,要根据已知条件进行逐层解读,逐层分析,进而将复杂事件逐渐向简单事件转化,这样可以应用计算公式轻松求解问题.
另外,数据处理也是学好概率与统计所必备的关键能力,其一般要经过收集、整理、提取、建模等过程,综合性更强,然限于篇幅,对于数学处理就不再详细阐述.总之,基于核心素养的概率统计教学,有助于帮助学生走出教考困境,有助于培养学生的核心竞争力,有助于学生综合学力的全面提升.

