考虑测量零偏的半挂车辆侧向速度校正估算方法

【摘要】为准确估算自动驾驶半挂车辆的牵引车侧向速度，提出了一种考虑传感器测量零偏的校正估算方法。在三自由度车辆动力学模型的基础上，将前轮转角、横摆角速度零偏和侧向加速度零偏等扩围到状态变量中，建立了测量零偏估计模型，考虑到动力学模型失配的影响，设计了基于运动学模型的反馈校正机制，对侧向速度和横摆角速度的估计结果进行反馈调节，利用平方根容积卡尔曼滤波算法实现该方法，并分析了估计器的可观性，最后，基于TruckSim与MATLAB/Simulink联合仿真平台进行了验证，结果表明：该方法不仅可以消除测量零偏的影响，还具有良好的收敛速度，性能明显优于未考虑测量零偏和仅考虑测量零偏的估算方法。

关键词：半挂车辆 侧向速度估算 测量零偏 反馈校正 平方根容积卡尔曼滤波

中图分类号：U461.91   文献标志码：A   DOI： 10.20104/j.cnki.1674-6546.20240121

Lateral Velocity Correction Estimation for Semi-Trailer Vehicles Considering Measurement Bias

Zhang Zhida

（Shanghai UTOPILOT Technology Company Ltd.， Shanghai 200438）

【Abstract】A correction estimation method considering sensor measurement bias was proposed to accurately estimate the lateral velocity of the tractor in autonomous semi-trailer vehicles. Based on the three-degree-of-freedom vehicle dynamics model， the measurement bias estimation model was established by expanding the front wheel angle， yaw rate bias， and lateral acceleration bias into the state variables. Taking into account the impact of dynamic model mismatch， a feedback correction mechanism based on the kinematic model was designed to adjust the estimation results of lateral velocity and yaw rate through feedback. The proposed method was implemented using the square-root cubature Kalman filter algorithm， and the observability of the estimator was analyzed. This method was verified on the joint simulation platform of TruckSim and MATLAB/Simulink. The results show that the proposed method not only eliminates the influence of measurement bias but also exhibits good convergence speed. Its performance is significantly better than estimation methods that do not consider measurement bias or only consider measurement bias.

Key words： Semi-trailer， Lateral velocity estimation， Measurement bias， Feedback correction， Square-root cubature Kalman filter

【引用格式】张志达. 考虑测量零偏的半挂车辆侧向速度校正估算方法[J]. 汽车工程师， 2024（6）： 14-21.

ZHANG Z D. Lateral Velocity Correction Estimation for Semi-Trailer Vehicles Considering Measurement Bias[J]. Automotive Engineer， 2024（6）： 14-21.

1 前言

准确获取车辆状态是自动驾驶汽车有效决策和精准控制的前提。受成本和技术限制，并非所有车辆状态都能够被直接、精确地测量，因此，需要借助惯性测量单元（Inertial Measurement Unit，IMU）和全球定位系统（Global Positioning System，GPS）等对车辆的侧向速度、侧偏角或横摆角速度等状态变量进行实时估算[1-2]。

目前，车辆状态估算主要通过车辆的运动学模型、动力学模型结合卡尔曼滤波（Kalman Filter，KF）系列算法、递归最小二乘法（Recursive Least Squares，RLS）等进行[3]。基于运动学模型的估算方法对车辆参数、路面附着系数和行驶工况等具有良好的鲁棒性，但对传感器偏差、数据漂移和校准精度等造成的测量误差非常敏感[4-5]。Selmanaj等[6]基于纵、横向二自由度运动学模型设计纵向速度和侧向速度观测器，进而估算了车辆侧偏角。李小雨等[7]基于三自由度车辆模型和扩展卡尔曼滤波（Extended Kalman Filter，EKF）算法提出了一种结合运动学模型和几何方法的质心侧偏角估算方法。该方法可以提高估计精度，但需要提前获取路面附着系数。为消除基于纯运动学模型造成的积分偏差，Rezaeian等[8]利用基于LuGre轮胎模型得到的轮胎侧偏角计算侧向速度，并与基于运动学模型估计的侧向速度进行加权，然而，该方法中前、后轮胎侧偏角的计算也需要路面附着系数。事实上，路面附着系数的测量和估算成本远高于侧向速度和质心侧偏角[9]。

基于动力学模型的车辆状态估算方法主要依赖于受作用力和扭矩激励的车辆模型和轮胎模型，采用的算法与基于运动学模型的方法基本一致。该方法受车辆和轮胎参数的影响较大，部分方案也需要提前获知路面附着系数。耿国庆等[10]提出了一种基于二自由度动力学模型和噪声自适应EKF算法的车辆状态估算方法。Reina等[11]在假设纵向速度恒定的情况下，结合二自由度车辆模型和EKF算法，设计了用于识别质心侧偏角等状态的估计器，该研究与文献[10]类似，都将轮胎模型考虑为线性，仅适用于车辆转向幅度较小的工况。Amin等[12]结合三自由度车辆动力学模型和LuGre轮胎模型，提出了一种基于约束无迹卡尔曼滤波（Constrained Unscented Kalman Filter，CUKF）算法的半挂车辆侧向速度估算方法，由于利用了LuGre轮胎模型，需要提前获知路面附着系数。另外，Piyabongkarn等[13]结合动力学模型和运动学模型设计了一种基于频率加权的车辆质心侧偏角估算方法，在低频转向时采用动力学模型的估算结果，在高频转向时采用运动学模型的估算结果。然而，以上研究均未综合考虑测量零偏和参数时变的影响。

鉴于此，本文提出一种考虑传感器测量零偏的半挂车辆侧向速度校正估算方法。基于三自由度车辆动力学模型，将前轮转角、横摆角速度零偏和侧向加速度零偏等扩围到估计器的状态变量中，建立测量零偏估算模型。针对参数时变造成的动力学模型失配，设计基于运动学模型的反馈校正机制，对侧向速度和横摆角速度的估算结果进行实时调节。最后，利用平方根容积卡尔曼滤波（Square-root Cubature Kalman Filter，SCKF）算法实现该方法，分析估计器的可观性，并基于TruckSim和MATLAB/Simulink联合仿真平台，选取不同输入和测量零偏工况测试该估算方法的有效性。

2 半挂车辆动力学模型

忽略路面坡度的影响，假设车辆仅做平面运动，建立考虑半挂车辆横向运动、横摆运动和折叠运动的三自由度动力学模型，如图1所示。其中：m1、m2分别为牵引车、挂车的质量，Iz1、Iz2分别为牵引车、挂车的横摆转动惯量，a1、b1分别为牵引车前、后轴至其质心的距离，c、a2分别为铰接点至牵引车质心、挂车质心的距离，b2为挂车后轴至其质心的距离，Fyf、Fyr分别为牵引车前、后轴轮胎侧向力，Fyt为挂车后轴轮胎侧向力，δf为牵引车的前轮转角，vx1、vx2分别为牵引车、挂车的纵向速度，vy1、vy2分别为牵引车、挂车的侧向速度，v1、v2分别为牵引车、挂车的速度矢量和，γ1、β1分别为牵引车的横摆角速度、质心侧偏角，γ2、β2分别为挂车的横摆角速度、质心侧偏角，θ为牵引车与挂车的相对角度，即折叠角。当折叠角较小时，可以认为vx1=vx2=vx，其中vx为纵向速度。

半挂车辆系统的动力学方程如下：

m1ay1=Fyf+Fyr-Fyh （1）

[Iz1γ1=a1Fyf+b1Fyr-cFyh] （2）

m2ay2=Fyt+Fyh （3）

[Iz2γ2=a2Fyh-b2Fyt] （4）

式中：[ay1=vy1+vxγ1]、[ay2=vy2+vxγ2]分别为牵引车、挂车的侧向加速度，Fyh为铰接点处的相互作用力。

在铰接点处，有如下耦合关系[12]：

[γ2=γ1+θ] （5）

[νy2=νy1-（a2+c）γ1-a2θ-νxθ] （6）

消除耦合项后可得：

[Iz1γ1+m1cνy1=-m1cνxγ1+a1Fyf-b1Fyr+c（Fyf+Fyr）]（7）

[（m1+m2）νy1-m2（a2+c）γ1-m2a2θ=][-（m1+m2）νxγ1+Fyf+Fyr+Fyt] （8）

[Iz2（γ1+θ）+m1a2νy1=-m1a2νxγ1+a2（Fyf+Fyr）-b2Fyt]

（9）

利用线性轮胎模型描述牵引车前、后轴和挂车后轴的轮胎力Fyi=kiαi， i=f，r，t。其中：ki为各轮胎侧偏刚度，αi为各轮胎侧偏角，f、r、t分别表示牵引车前轴、牵引车后轴、挂车后轴。根据图1的坐标系定义，牵引车前、后轮胎和挂车后轮胎的侧偏角分别为：

αf[ =δf-νy1+a1γ1νx] （10）

αr[ =b1γ1-νy1νx] （11）

αt=[θ-νy1-（a2+b2+c）γ1-（a2+b2）θνx] （12）

综上，半挂车辆动力学模型的微分方程为：

[Mx+Gx=Fδf] （13）

式中：x=[νy1γ1θθ]为状态变量，M=[m1cm1+m2m1a20-Iz1m2（a2+c）Iz200-m2a2Iz20  0001]为[x]的系数矩阵，G为x的系数矩阵，F=[（a1+c）kfkfa2kf0]为δf的系数矩阵。

其中，x的系数矩阵G的表达式为：

经过整理，可得半挂车辆动力学模型的状态空间方程为：

[x]=Ax+Bδf （15）

式中：A=-M-1G为状态转移矩阵，B=M-1F为控制矩阵。

3 侧向速度估计器设计

3.1 考虑测量零偏的估计模型

受成本和技术限制，并非所有车辆状态都能够被直接测量。部分车辆状态参数随时间或工况变化，增加了车辆模型的不确定性。因此，基于估计算法的虚拟观测器成为获取某些车辆状态的重要手段。然而，由于模型具有非完整性，如参数时变、未建模部分和外界扰动等，通常会引入模型失配问题。鉴于此，本文在估计牵引车侧向速度时，考虑横摆角速度和侧向加速度的零偏，以降低模型非完整性的影响。所采用的测量变量为横摆角速度、侧向加速度和前轮转角等易于获取的状态。结合车辆动力学模型和运动学模型，定义状态转移方程为：

[xk=f（xk-1，uk-1）+wk-1] （16）

式中：[xk=（vyk，γk，θk，vyk，γk，θk，ayk，δfk，dγk，dayk）T]为估计器在离散时间k时刻的状态变量，[uk-1]为控制变量，f（ ）为状态转移方程，wk-1为过程噪声，dγk、dayk分别为横摆角速度零偏、侧向加速度零偏。

为便于后续说明，定义vy=vy1，γ=γ1。其中，状态转移方程的表达式为：

式中：T为离散时间步长。

定义侧向速度估计器的测量方程为：

[zk=h（xk）+vk] （18）

其中：

[h1：γmk=γk+dγk-1h2：aymk=ayk+dayk-1h3：δfmk=δfk] （19）

式中：zk=[γmk，aymk，δfmk]T为k时刻的测量变量；h（ ）为测量方程；υk为测量噪声；γmk为横摆角速度测量值；aymk为侧向加速度测量值；δfmk为前轮转角测量值，由转向盘转角转换获取。

3.2 基于运动学模型的反馈校正

当半挂车辆行驶工况复杂多变时，不确定的工作环境可能会导致动力学模型的失配，从而造成估算结果出现误差。为进一步降低模型非完整性的影响，在消除传感器测量零偏的基础上引入基于运动学模型的反馈校正，该反馈校正为基于状态变量之间运动学关系以及估算值与测量值之间偏差引入的闭环调节，包括侧向速度反馈调节和横摆角速度反馈调节。

侧向速度反馈调节是利用估算的侧向速度与运动学积分得到的侧向速度之间的偏差补偿侧向速度项。其中，侧向速度偏差为：

[Δνy=νy-0t（aym-day）-νx（γm-dy）] （20）

式中：[vy]为侧向速度估算结果， t为估算时间。

横摆角速度反馈调节是利用估算的横摆角速度与测量的横摆角速度之间的偏差补偿横摆角速度项。其中，横摆角速度偏差为：

[Δγ=γ-（γm-dγ）] （21）

因此，引入反馈校正后，式（17）的前2项可换算为：

[νyk=νyk-1+νyk-1T-kvyΔvyk-1] （22）

[γk=γk-1+γk-1T-kγΔγk-1] （23）

式中：kvy为侧向速度项的调节增益，kγ为横摆角速度项的调节增益。

3.3 SCKF估计算法

鉴于SCKF算法在估计精度和数值稳定性方面的优势，选取该算法估算半挂车辆的侧向速度。标准SCKF算法的实现过程如下[14]：

a. 初始化。给定状态初始值[x0|0]，计算误差协方差矩阵平方根因子的初始值[S0|0=P0|0]，其中P0|0为误差协方差矩阵。

b. 时间更新。计算状态容积点并基于状态转移方程传递：

[xik-1k-1=xk-1k-1+Sk-1k-1ξi， i=1，2，…，2nxi*kk-1=f（xik-1k-1，uk-1）] （24）

式中：ξi为容积点权重矩阵[[nIn，-nIn]]的第i列，In为n×n的单位矩阵，n为状态变量的维数。

计算状态变量的预测值及其误差协方差矩阵的平方根因子：

[xkk-1=12ni=12nxi*kk-1Skk-1=qr（[Xi*kk-1，Qk-1]）] （25）

式中：Qk-1为过程噪声协方差，[X*kk-1=12n[x1*kk-1-xkk-1，x2*kk-1-xkk-1，…，x2n*kk-1-xkk-1]]为加权中心矩。

c. 测量更新。更新状态容积点并基于测量方程传递：

[xikk-1=xkk-1+Skk-1ξizikk-1=h（xikk-1）] （26）

计算测量变量的预测值及其新息协方差矩阵的平方根因子：

[zkk-1=12ni=12nzikk-1Szzkk-1=qr（[Zkk-1，Rk]）] （27）

式中：Rk为测量噪声协方差，[Zkk-1=12n[z1kk-1-z1kk-1，z2kk-1-zkk-1，…，z2nkk-1-zkk-1]]为加权中心矩。

测量变量的协方差矩阵和互协方差矩阵分别为：

[Pzzkk-1=Szzkk-1（Szzkk-1）TPxzkk-1=Xkk-1ZTkk-1] （28）

式中：[Xkk-1=12n[x1kk-1-x1kk-1，x2kk-1-xkk-1，…，x2nkk-1-xkk-1]]为加权中心矩。

卡尔曼滤波增益矩阵为：

Kk=[Pxzkk-1（Pzzkk-1）-1] （29）

更新状态变量估算值和误差协方差矩阵的平方根因子为：

[xkk=xkk-1+Kk（zk-zkk-1）Skk=qr（[xkk-1Kkzk-zkk-1，KkRk]）] （30）

3.4 可观性分析

在编程实现估计器前，需验证其可观测性，这决定了是否可以从系统的输入和外部输出信息中正确推导出内部状态。对于非线性估计器而言，通常主要关注其在当前状态的局部可观性，即利用离散线性时不变系统可观性矩阵的秩来判断非线性系统的局部可观测性：

OLTI=[Hk HkFk … HkFk（n-1）T] （31）

式中：OLTI为线性时不变系统可观性矩阵，若OLTI满秩，则非线性系统局部可观；Fk、Hk分别为k时刻的状态转移矩阵、测量矩阵，即f（ ）和h（ ）的雅克比矩阵。

Fk、Hk的表达式分别为：

[Hk=010000001000000010010000000100] （33）

利用MATLAB的Rank函数求解估计器可观性矩阵OLTI的秩，输出结果为10，证明所设计的估计器是局部可观的。

4 仿真验证

为验证所提出的考虑测量零偏的半挂车辆侧向速度校正估算方法的效果，基于TruckSim和MATLAB/Simulink在正弦输入和阶跃输入2种工况下开展联合仿真。其中，半挂车辆模型的主要参数为：m1=8 036 kg，Iz1=4.87×104 kg·m2，m2=22 570 kg，Iz2=3.94×105 kg·m2，a1=1.6 m，b1=2.05 m，a2=5.4 m，b2=3.4 m，c=1.5 m，kf=3.70×105 N/rad，kr=9.37×105 N/rad，kt=1.33×106 N/rad。分别在不考虑测量零偏和反馈校正、仅考虑测量零偏、同时考虑测量零偏和反馈校正的条件下开展估算，结果分别记作SCKF估计1、SCKF估计2、SCKF估计3。本文仅关注如何消除测量零偏，噪声异常的处理采用前期研究的方法[9，15]。

4.1 正弦输入工况

在正弦输入仿真工况中，设置车速vx=80 km/h，前轮转角δf输入如图2所示，周期为6 s。同时，设置侧向加速度零偏为0.2 m/s2，用于模拟传感器单一测量信号存在的零偏。

为评估所提出的考虑测量零偏校正估计方法的性能，选取侧向速度、侧向加速度、横摆角速度、侧向加速度零偏和横摆角速度零偏的估算结果作为对比指标。正弦输入工况下，侧向速度、侧向加速度和横摆角速度的估算结果如图3所示。由图3a可知，SCKF估计2和SCKF估计3可以准确估算出半挂车辆的侧向速度，而SCKF估计1的估算结果存在明显偏差。这是因为SCKF估计2和SCKF估计3在设计估计器时均考虑了传感器的测量零偏。同时，观察图3a可以发现，考虑反馈校正的SCKF估计3的侧向速度估算结果收敛速度和精度均优于SCKF估计2。图3b和图3c同样表明，SCKF估计3的估算结果更准确。由于未考虑测量零偏，SCKF估计1的侧向加速度估算值依然存在0.2 m/s2的偏差。因为估算模型中考虑了测量零偏，SCKF估计2和SCKF估计3的横摆角速度估算结果也需要一定的收敛时间。

图4所示为正弦输入工况下侧向加速度零偏和横摆角速度零偏的估算结果。由图4a和图4b可知，SCKF估计2和SCKF估计3均能较为准确地估算出侧向加速度和横摆角速度的测量零偏。由于SCKF估计3同时考虑了基于运动学模型的反馈校正，其收敛速度更快、估算精度更高，图4a的前2 s更为明显。因此，考虑测量零偏的半挂车辆侧向速度校正估算方法不仅能够估算出传感器的测量零偏，还可以有效提高估算结果的收敛速度。

4.2 阶跃输入工况

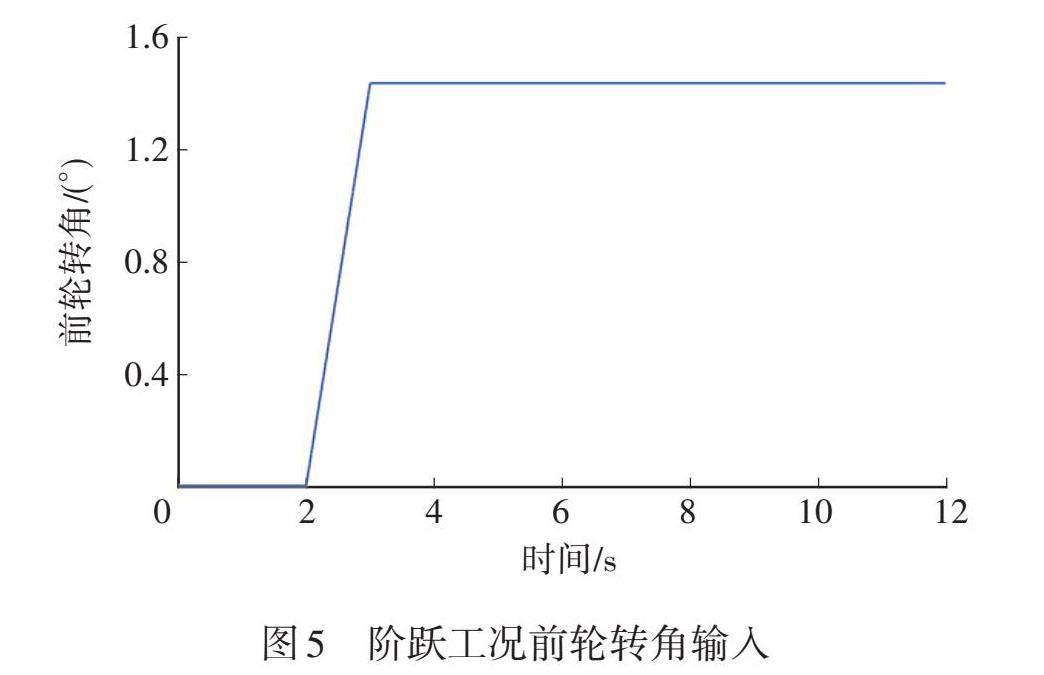
为进一步验证SCKF估计3对行驶工况和测量零偏的适应性，进行同时考虑多个测量零偏的阶跃输入工况仿真分析。设置车速vx=70 km/h，前轮转角δf输入如图5所示。同时，设置侧向加速度零偏和横摆角速度零偏分别为0.2 m/s2和0.04 rad/s，用于模拟传感器多个测量信号存在的零偏。

阶跃输入工况下，侧向速度、侧向加速度和横摆角速度的估算结果如图6所示。由图6a可知，SCKF估计2和SCKF估计3同样可以准确估算出半挂车辆的侧向速度。然而，SCKF估计1的估算结果不仅存在明显的偏差，且收敛速度较慢。由图6a可知，SCKF估计3的侧向速度估算效果明显优于SCKF估计1和SCKF估计2。由图6b和图6c可知，SCKF估计2和SCKF估计3能够有效消除侧向加速度和横摆角速度估算结果的测量零偏，由于SCKF估计1没有考虑测量零偏，估算结果依然与其测量值一致。由图6中的估算结果可知，SCKF估计3的整体性能最优。

图7所示为阶跃输入工况下侧向加速度零偏和横摆角速度零偏的估算结果。该工况下的SCKF估计2和SCKF估计3均能较为准确地估算出侧向加速度和横摆角速度的测量零偏，且对测量零偏的差异均有较好的适应性。但由图7a和图7b中前2 s数据可知，SCKF估计3的收敛速度和精度更好。

通过对比不同输入工况和测量零偏的仿真结果可知，SCKF估计3可准确估算出半挂车辆的侧向速度，消除侧向加速度和横摆角速度的测量零偏，整体效果，尤其是收敛速度均优于SCKF估计2。

5 结束语

本文针对自动驾驶半挂车辆侧向速度估算中的传感器测量零偏问题，提出了一种结合动力学模型和运动学模型的反馈校正估算方法。在SCKF算法框架下，利用基于车辆动力学的估算模型消除侧向加速度和横摆角速度测量零偏的影响。为避免动力学模型失配的影响，基于状态变量之间的运动学关系，反馈调节了侧向速度和横摆角速度的估算结果。

TruckSim和MATLAB/Simulink联合仿真结果表明，该方法能够准确估算出半挂车辆的侧向速度，消除侧向加速度和横摆角速度的测量零偏，其整体性能，尤其是收敛速度，明显优于不考虑测量零偏和仅考虑测量零偏的估计方法。

参考文献

[1]   SINGH K B， ARAT M A， TAHERI S. Literature Review and Fundamental Approaches for Vehicle and Tire State Estimation[J]. Vehicle System Dynamics， 2019， 57（11）： 1643-1665.

[2]   JIN X J， YIN G D， CHEN N. Advanced Estimation Techniques for Vehicle System Dynamic State： A Survey[J]. Sensors， 2019， 19（19）： 4289.

[3]   LIU W， XIA X， XIONG L， et al. Automated Vehicle Sideslip Angle Estimation Considering Signal Measurement Characteristic[J]. IEEE Sensors Journal， 2021， 21（19）： 21675-21687.

[4]   WANG Z P， WU J Y， ZHANG L， et al. Vehicle Sideslip Angle Estimation for a Four-Wheel-Independent-Drive Electric Vehicle Based on a Hybrid Estimator and a Moving Polynomial Kalman Smoother[J]. Proceedings of the Institution of Mechanical Engineers， Part K Journal of Multi-Body Dynamics， 2019， 233（1）： 125-140.

[5]   张志达. 基于车路状态估计的智能汽车运动决策与控制方法研究[D]. 重庆： 重庆大学， 2021.

ZHANG Z D. Research on Motion Decision and Control of Intelligent Vehicle Based on Vehicle-Road State Estimation[D]. Chongqing： Chongqing University， 2021.

[6]   SELMANAJ D， CORNO M， PANZANI G， et al. Vehicle Sideslip Estimation： A Kinematic Based Approach[J]. Control Engineering Practice， 2017， 67（10）： 1-12.

[7]   李小雨， 许男， 郭孔辉. 基于运动学方法和运动几何方法融合的质心侧偏角估计[J]. 机械工程学报， 2020， 56（2）： 121-129.

LI X Y， XU N， GUO K H. Vehicle Sideslip Angle Estimation Based on Fusion of Kinematic Method and Kinematic-Geometry Method[J]. Journal of Mechanical Engineering， 2020， 56（2）： 121-129.

[8]  REZAEIAN A， KHAJEPOUR A， MELEK W， et al. Simultaneous Vehicle Real-Time Longitudinal and Lateral Velocity Estimation[J]. IEEE Transactions on Vehicular Technology， 2017， 66（3）： 1950-1962.

[9]  ZHANG Z D， ZHNEG L， WU H， et al. An Estimation Scheme of Road Friction Coefficient Based on Novel Tyre Model and Improved SCKF[J]. Vehicle System Dynamics， 2022， 60（8）： 2775-2804.

[10] 耿国庆， 韦斌源， 江浩斌， 等. 基于NA-EKF的分布式驱动电动汽车行驶状态估计研究 [J]. 汽车工程， 2018， 40（7）： 770-776.

GENG G Q， WEI B Y， JIANG H B， et al. A Research on Driving State Estimation for Distributed Drive Electric Vehicle Based on NA-EKF[J]. Automotive Engineering， 2018， 40（7）： 770-776.

[11] REINA G， MESSINA A. Vehicle Dynamics Estimation Via Augmented Extended Kalman Filtering[J]. Measurement， 2018， 133： 383-395.

[12] AMIN H K， AMIR K， BARIS F. Vehicle-Trailer Lateral Velocity Estimation using Constrained Unscented Transformation[J]. Vehicle System Dynamics， 2022， 60（3）： 1048-1075.

[13] PIYABONGKARN D， RAJAMANI R， GROGG J A， et al. Development and Experimental Evaluation of a Slip Angle Estimator for Vehicle Stability Control[J]. IEEE Transactions on Control Systems Technology， 2009， 17（1）： 78-88.

[14] ZHANG Z D， ZHENG L， LI Y N， et al. Cooperative Strategy of Trajectory Tracking and Stability Control for 4WID Autonomous Vehicles under Extreme Conditions[J]. IEEE Transactions on Vehicular Technology， 2023， 72（3）： 3105-3118.

[15] 张志达， 郑玲， 李以农， 等. 基于鲁棒自适应SCKF的智能汽车目标状态跟踪研究[J]. 机械工程学报， 2021， 57（20）： 181-193.

ZHANG Z D， ZHENG L， LI Y N， et al. Research on Intelligent Vehicle Target State Tracking Based on Robust Adaptive SCKF[J]. Journal of Mechanical Engineering， 2021， 57（20）： 181-193.

（责任编辑 弦 歌）

修改稿收到日期为2024年5月8日。